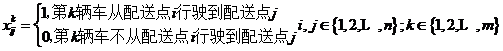粒子群算法在物流运输车辆优化调度中的应用研究毕业论文
2020-02-19 07:51:08
摘 要
在交通发展迅速的今天,物流是经济发展中不可或缺一环。而车辆路径问题(Vehicle Routing Problem,VRP)是物流配送的核心问题。因此本文以物流配送为背景,对基于粒子群算法的车辆调度问题进行研究。首先,对车辆路径问题进行分类,总结已有的车辆路径问题求解算法,然后给出有能力约束的车辆路径问题(CVRP)和软时间窗的车辆路径问题(VRPSTW)数学模型。其次,对求解车辆路径问题的粒子群算法的粒子编码方式和改进方案进行综述。文章基于求解TSP的离散粒子群算法引入新的邻域结构,改进速度更新公式,并引入文化基因算法的选择操作和2-opt局部搜索算子,形成文化基因粒子群混合算法。最后,将上述算法应用到CVRP和VRPTW,并与其他算法对比,结果表明本文算法有较强全局搜索能力且有效避免过早收敛。
关键词:车辆路径问题;物流配送;文化基因算法;粒子群算法
Abstract
Nowadays, with the rapid development of and transportation, logistics is an indispensable part of economic development. Vehicle Routing Problem (VRP) is the core issue of logistics distribution. Therefore, this thesis studies the Vehicle Routing Problem by Particle Swarm Optimization based on modern logistics technology. The main contributions of this paper are as follows: Firstly, Vehicle Routing Problem is classified and existing Vehicle Routing Problem solving algorithms are summarized. Then the mathematical model of Capacitated Vehicle Routing Problem and Vehicle Routing Problem with Soft Time Windows are given. Secondly, the Particle Swarm Optimization algorithm for solving vehicle routing problem is reviewed. The particle coding methods and improved schemes of PSO are summarized. In this paper, a neighborhood structure is introduced, a new velocity update rule is proposed, and the select operation and 2-opt local search operation of Memetic Algorithm are introduced based on the Discrete Particle Swarm Optimization to solve the TSP. Finally, the above algorithm is applied to CVRP and VRPTW, and compared with other algorithms, the results verify that this algorithm not only maintains good global search capability, but also effectively prevent premature convergence.
Key Words:Vehicle Routing Problem;logistics distribution;Memetic Algorithm;Particle Swarm Optimization
目录
第1章 绪论 1
1.1 研究背景与意义 1
1.2 国内外研究现状 2
1.2.1 国外研究现状 2
1.2.2 国内研究现状 3
1.3 论文主要研究内容 3
1.4 本章小结 4
第2章 常见模型算法分析与车辆调度优化模型建立 5
2.1 物流配送路径问题分类 5
2.2 求解算法分类 5
2.3 有容量约束的车辆优化调度数学模型 6
2.4 软时间窗的车辆优化调度数学模型 7
2.5 本章小结 9
第3章 粒子群算法 10
3.1 标准粒子群算法 10
3.2 针对VRP的粒子的编码方式 11
3.3 粒子群算法常见改进研究 13
3.3.1 惯性因子和学习因子改进 13
3.3.2 带收缩因子的速度更新改进 14
3.3.3 加强局部搜索的改进 15
3.3.4 与其他启发式算法混合 17
3.4 文化基因粒子群混合算法设计 17
3.4.1 编码方式 18
3.4.2 粒子群算法离散化策略 19
3.4.3 算法实现具体步骤 20
3.5 本章小结 21
第4章 改进粒子群算法求解车辆路径问题 23
4.1 有容量约束车辆路径问题仿真 23
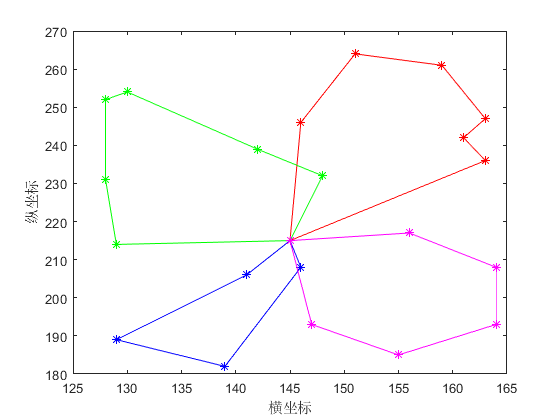
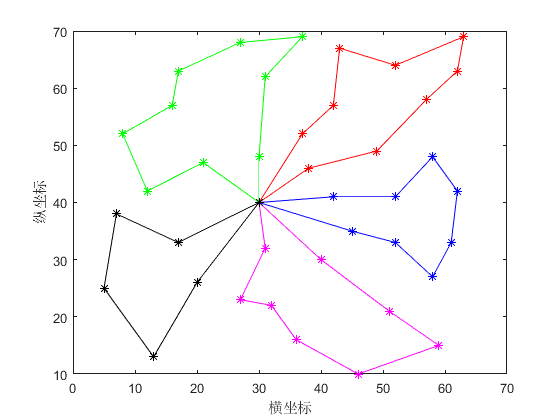
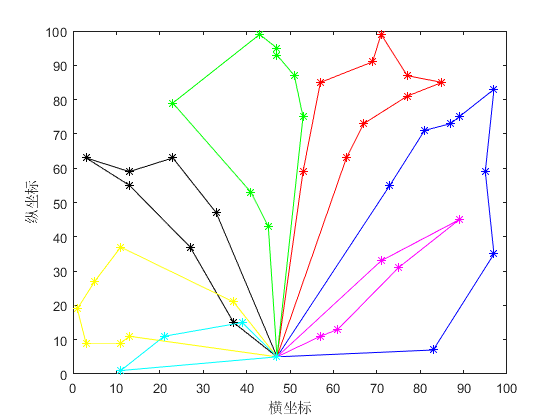
4.1.1 算例一 23
4.1.2 算例二 24
4.1.3 算例三 26
4.1.4 算例四 28
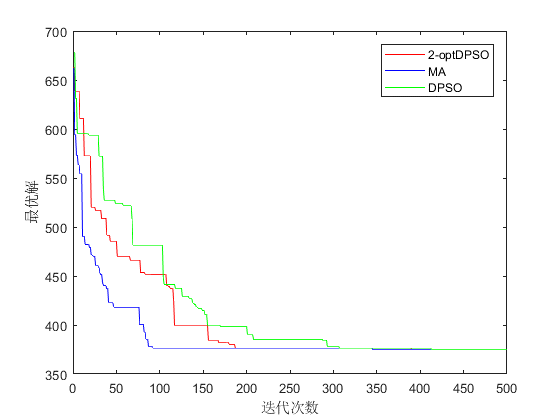
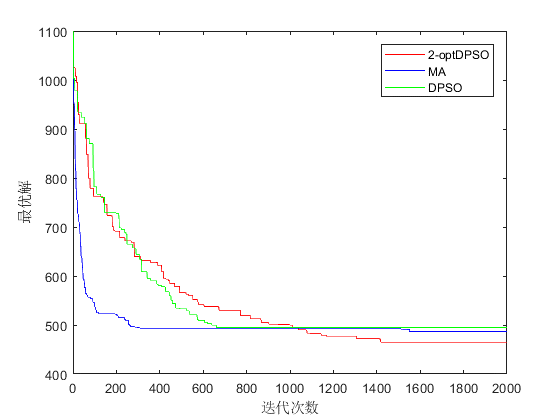
4.1.5 结果分析 30
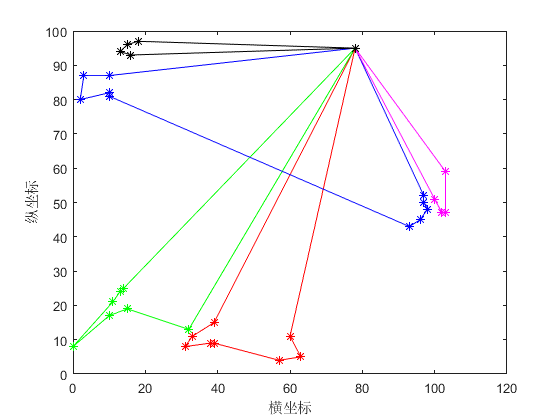
4.2 软时间窗车辆路径问题仿真 32
4.2.1 算例一 32
4.2.2 算例二 33
4.2.3 算例三 35
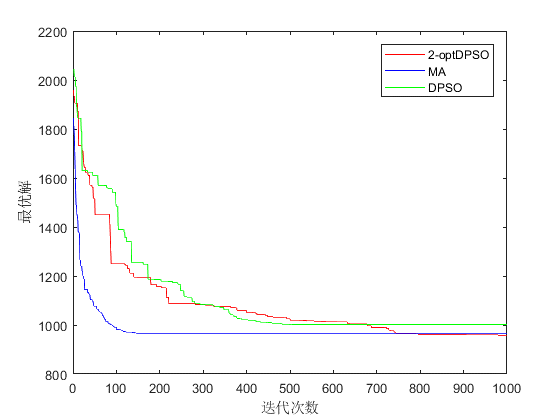
4.2.4 结果分析 37
4.3 本章小结 38
第5章 结论与展望 39
5.1 总结 39
5.2 展望 39
参考文献 41
致谢 45
绪论
研究背景与意义
在全球经济一体化的世界背景下,国家的经济发展经济交流以及现代科学技术的发展一直在稳步发展,而作为一个服务行业,物流产业在社会生产经济生活中扮演重要的角色。彼得·杜克拉称物流是“第三利润源泉”。物流承担着社会生产物资的运输工作,如果运输工作好比人体的血液输送各种营养物质,那么物流便是提供动力的心脏,社会发展的“加速器”。随着社会生产力的不断提高,流通领域的竞争会逐步加大,而生产领域的竞争空间则会被压缩,因此也称物流为产业结构演变的“润滑剂”。
我国物流仍然处于快速发展的时期,这个时期要把握好战略机遇同时积极面对未来新的矛盾和问题。现在物流业亟需解决的一个重要问题便是如何降低物流成本。根据中国物流与采购联合会统计可知我国物流效率每年都在逐步提高。另一方面,我国2000年物流总费用与近年来相比差距不大,2018年我国物流运输效率提高较为缓慢,但近年来运输费用的降本增效成效比较显著。因此,我国物流未来发展主要考虑的是如何降低物流成本。
调度优化是物流配送活动中非常重要的工作,对节约企业资源,提高客户服务的质量十分重要。车辆路径优化是物流配送中的重要步骤。合理的配送路线可以显著提高车辆配送效率、降低物流企业货物运输成本和车辆成本。车辆路径问题(Vehicle Routing Problems)要求根据车辆的装载量、服务时间等限制对车辆配送行驶路线进行规划,使得物流配送的成本最小化。如果配送过程中物流信息是动态变化的,则需要实时对车辆调度时间以及路线进行调整,以完成配送任务同时降低物流配送的成本。
物流配送系统是一个较为复杂的系统,常常因为一些不确定因素导致配送流程安排变得困难。这些干扰可能来自于交通因素,比如天气干扰、交通堵塞等;有些来自于客户配送需求,比如货物的时间窗需求、出现新的客户需求等。因此在基础VRP模型上,还需考虑基于实际情况的上许多延伸模型。比如,在随着逆向物流需求日益增多,基于节约成本等目的,第三方物流企业和自营物流企业常常将正向物流和逆向物流两种车辆调度结合,由此产生同时送取货车辆路径问题(Vehicle Routing Problem with Simultaneous Pickup and Delivery,VRPSPD);在现实生活中常常由于一些客观因素,比如交通堵塞或者客户工作时间要求,使得时间窗成为车辆路径问题中常见的限制因素。因此有时窗限制车辆路径问题(Vehicle Routing Problems with Time Windows,VRPTW)也成为车辆优化调度问题中广泛研究的模型。而将以上两种车辆调度问题相结合,即带时间窗和同时取送货的车辆路径问题(VehicleRouting Problem with Simultaneous Piekup and Delivery and Time Windows,VRPSPDTW)更具有复杂性。同时,车辆调度问题是NP难题,这就使得物流路径优化问题的求解变得极为复杂。
本文以优化现实物流企业配送成本为目标,建立车辆优化调度数学模型,并讨论不同VRP模型以及不同求解算法的优劣,之后采用改进粒子群算法求解车辆路径问题。本文的研究扩展了粒子群算法在VRP模型中的应用,具有一定理论和实际意义。
国内外研究现状
国外研究现状
1959年,Dantzig和Ramser[1]基于旅行商问题(Traveling Salesman Problem,TSP)得到启发,提出了车辆分配问题TDP(Truck Dispatching Problem)。半个世纪以来,许多学者从基本问题出发,根据不同的约束和目标,构建了不同的模型,并提出许多解决问题的精确求解算法和启发式算法。车辆路径问题一般模型是给定有多辆车的站点和需要配送服务的配送位置,要求车辆从站点出发遍历所有配送点,构造车辆路径,且所有配送点仅被访问一次。除此之外,针对现实情况车辆路径问题常常包含多种约束条件,比如每辆车的最大装载量限制、客户配送时间要求限制、车辆行驶距离限制等下,对目标函数进行优化,优化目标一般是总路程最短、时间最短、总费用最小等。车辆路径问题是旅行商问题的扩充,反之TSP是VRP的特例,两者转化关系是当VRP模型的车辆个数为1时VRP可以看成一个TSP问题。一辆车的VRP问题,即TSP问题是NP难题,所以可以得出结论VRP也是NP难题。
1964年Clarke和Wright[2]通过迭代方法求解VRP问题,即Clarke-Wright节约算法。在精确算法方面,Laporte[3]等人于1986年提出用分支定界法来解决车辆优化调度问题。1981年Cristofides[4]等人用K度中心树的搜索算法求解出有134个节点的VRP。1981年Fisher[5]等人针对有时间窗和容量要求的VRP提出了三下标车辆流方程,求得最小规模的车队。在启发式算法方面,Gillett[6]等人首次提出Sweep算法。Paolo Toth和Daniele Vigo[7] 对VRP的许多扩展模型进行归纳,总结VRP早期求解方法,即精确求解方法,以及许多启发式算法。Sungur[8]等人针对多车型VRP提出用鲁棒性最有方法。
车辆路径优化在实际生活中的应用也日趋成熟,许多国家开发了智能交通系统(Intelligent Traffic System,ITS)来解决实际社会中的车辆调度问题。80年代以来,智能交通系统一直处于高速发展时期,现在主要的ITS是美国、欧洲和日本。目前,在实际的动态车辆调度系统中已经包含了一些较成熟的算法。美国的配送系统在运输车路径优化和车辆分配上效果显著,提高了运输效率,降低了物流成本。IBM公司的VIIPX系统,富士通公司VSS系统,美孚公司HOCAD系统是目前应用于实际社会生产中的车辆调度系统。
国内研究现状
我国学者对车辆调度优化问题的研究上多数集中在启发式算法。以粒子群算法为例,徐杰[9]等将变异引入粒子群算法求解多目标时间窗车辆优化调度问题,实验验证该算法有效性。郭森[10]等在基本粒子群算法上加入动态学习和突变因子,在基准函数测试和多目标车辆路径问题实例优化中效果良好。马艳芳[11]等在车辆路径优化模型中引入模糊随机理论,并用基于模糊随机算子的改进粒子群算法求解。周蓉[12]等针对软硬时间窗共存装卸一体化车辆路径问题,在粒子群算法中引入变邻域下降搜索算法,通过算例仿真验证算法有效性。在粒子群算法的改进方面,较多学者将粒子群算法与其他启发式算法混合。马慧民[13]等提出模拟退火粒子群混合算法,在粒子群加入模拟退火概率突跳性避免了粒子群算法陷入局部最优。寇明顺[14]等提出蜂群粒子群混合算法,将最优粒子作为蜂王与雄蜂随机概率进行交叉操作,提高粒子群算法的全局搜索能力,在有容量约束的车辆路径问题模型求解上优于其他启发式算法。凌海峰[15]等提出蚁群粒子群混合算法,混合算法兼顾蚁群算法的全局搜索能力和粒子群算法的局部搜索能力,仿真显示该算法在求解容量约束VRP问题上搜索速度快,寻优能力强。
除此之外,也有其他启发式算法应用于VRP求解上。彭春林[16]等对遗传算法交叉算子进行改进,通过仿真说明改进的遗传算法优化结果较好,稳定性高。杨福兴[17]等提出一种结合时变策略的改进型最大最小蚁群算法,以Solomon测试集进行仿真,结果表明该算法求解精度高,收敛速度快。王健[18]等建立公交车辆调度优化模型,然后用遗传算法求解公交车路径优化问题,实验表明遗传算法求解可以满足定制公交企业的实时性需求。夏扬坤[19]等针对时间窗车辆路径问题,设计了自适应禁忌搜索算法,由带时间窗车辆路径问题测试算例表明算法的有效性。潘震东[20]等考虑多点运输的具有柔性车辆能力的带货物权重的车辆路径问题,建立了带货物权重的VRP模型,开发一种基于划分的遗传算法,算法仿真与标准遗传算法和其他启发式算法对比,说明提出的改进遗传算法解的质量较高。
论文主要研究内容
本论文将分为五章,主要内容分别为:
第一章,绪论。对车辆路径问题的研究背景与意义进行介绍,然后对车辆路径问题的国内外研究现状进行分析,最后对本文主要内容进行说明。
第二章,常见模型算法分析与车辆调度优化模型建立。介绍车辆路径问题的模型、基于不同约束条件下车辆路径问题的分类,以及车辆路径问题求解算法的分类。最后详细介绍有容量约束的车辆优化调度和软时间窗的车辆优化调度的数学模型。
第三章,粒子群算法。本文首先介绍标准粒子群算法基本原理和算法流程。其次,对车辆路径问题的粒子编码方式进行综述。再次,总结粒子群算法的常见改进方案。最后,针对求解TSP的离散粒子群算法容易陷入局部最优,对算法进行改进并提出文化基因离散粒子群混合算法,给出算法具体的实现步骤。
第四章,改进粒子群算法求解车辆路径问题。在前文模型建立、算法改进的基础上,用标准数据集测试改进粒子群算法在有容量约束的车辆优化调度问题和软时间窗车辆优化调度问题上的算法性能,并与其他算法进行对比,验证本文所建模型和算法设计的可行性和有效性。
第五章,结论与展望。对本文主要研究工作和结果进行总结,并提出本文改进粒子群算法在车辆调度优化上今后的研究方向。
本章小结
本章主要介绍在全球经济发展的背景下车辆路径问题研究的意义。对车辆路径问题模型建立、求解算法、实际应用的研究现状进行总结概括,最后对整个论文的结构安排进行详细介绍。
常见模型算法分析与车辆调度优化模型建立
本章主要对车辆路径优化模型进行分类,并归纳不同类型VRP模型建立的异同点。建立有容量约束的车辆优化调度模型以及有时间窗的车辆优化调度模型,并在后续工作中对这两类模型进行仿真。
物流配送路径问题分类
车辆路径问题按不同标准有不同分类:
(1)单车型问题和多车型问题。车型不同实际上表现为车辆容纳量不同,单车型问题指派送的车辆完全一样,一般模型中表示为所有车辆容量相同,而多车型问题刚好相反。
(2)按站点数目分,可分为单站点问题和多站点问题。单站点问题所有车从同一出发点出发再回到该站点,而多站点车辆可于不同站点出发。但多站点问题可以通过设置一个虚拟站点并将所有配送点和站点都作为虚拟站点的配送点来转化为单车场问题。
(3)配送问题和同时配送和取货问题。配送问题是指车辆在配送点只卸货进行操作,或者向客户收取货物。装卸混合问题中车辆经过配送点要同时考虑装货、卸货两种情况。
(4)无时间窗问题和有时间窗问题。时间窗是指配送点对车辆到达配送点的时间段限制。
(5)单目标优化问题和多目标优化问题。单目标优化问题的数学模型只有一个优化目标,而多目标优化问题是指有多个目标函数。
(6)车辆路径封闭问题和车辆路径开放问题。车辆路径封闭问题要求车辆最终返回出发点,构成哈密顿回路,即车辆从出发点出发,最后返回出发点。车辆开放问题允许车辆路径不是哈密顿回路。
(7)其他车辆路径优化问题。在实际物流配送中,物流约束条件是多种多样的,需要根据实际情况建立数学模型。
求解算法分类
车辆路线问题的求解算法包括精确算法和启发式解法两类。但VRP问题解空间大,主要的求解方法是启发式算法。相关的启发式方法主要分三类:构造启发式算法,改进启发式算法,亚启发式算法。VRP算法分类如图2‑1所示:
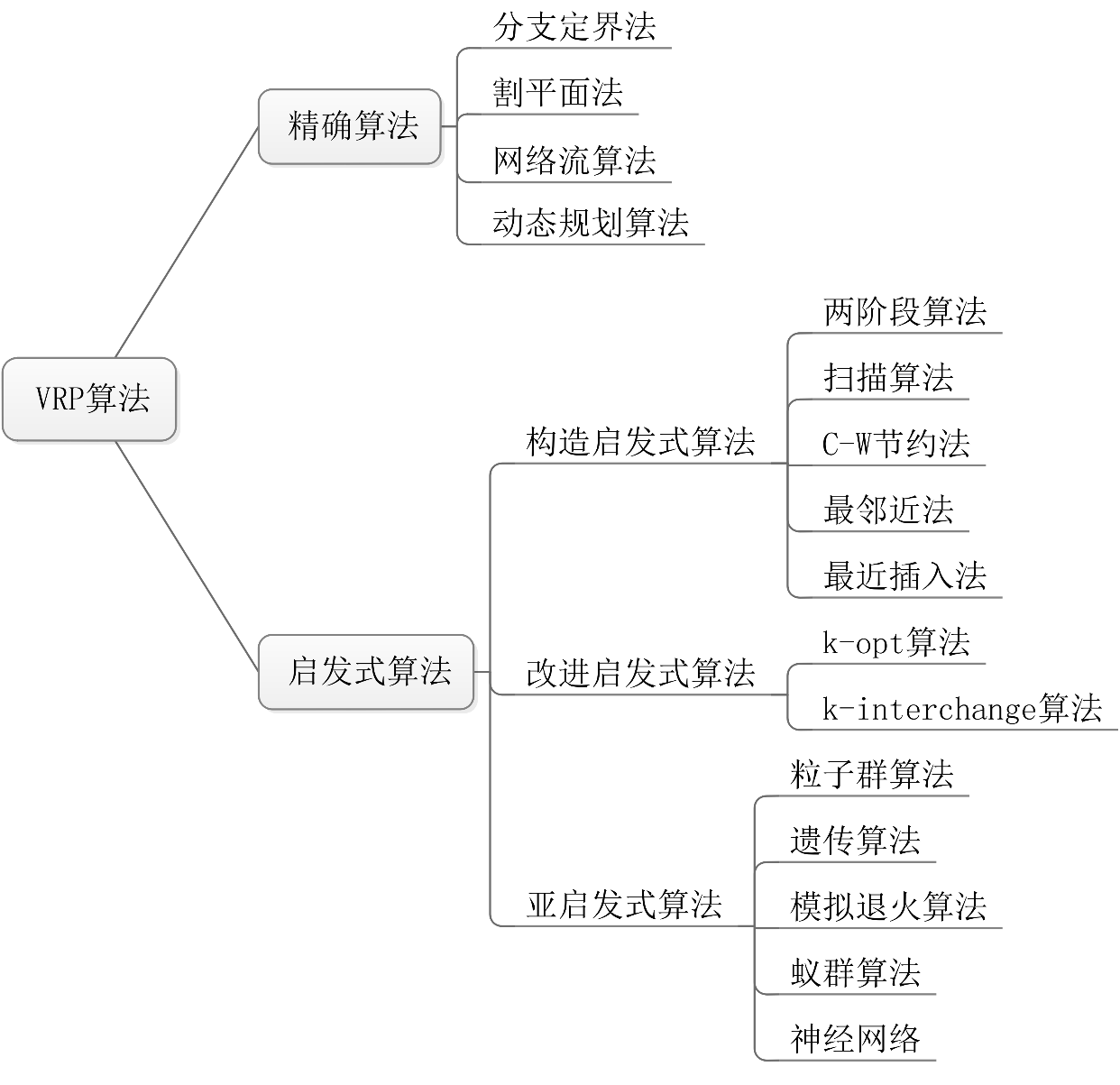
图 ‑ 车辆路径问题求解算法分类
构造启发式方法流程较为简单,求解速度也较快,但若VRP模型的配送点较多时很难找到满意的解。改进启发式算法在求解VRP问题上相比于构造启发式来说求解精度更高,但因其结构简单,在较大型的VRP问题上求解效率不高,因此常常作为亚启发式算法的局部搜索算子或者改进策略来使用。亚启发式算法是求解VRP问题的主流,已经有很多学者在亚启发式算法求解VRP上取得较好的效果。
有容量约束的车辆优化调度数学模型
记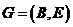 为赋权图,
为赋权图,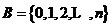 为顶点集顶点0为站点,即车辆出发点1~n为配送点,E为边集,各顶点间的距离为欧氏距离
为顶点集顶点0为站点,即车辆出发点1~n为配送点,E为边集,各顶点间的距离为欧氏距离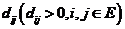 ,配送中心有m辆车,每辆车的最大装载量为C,每个客户的需求量为
,配送中心有m辆车,每辆车的最大装载量为C,每个客户的需求量为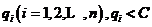 ,定义决策变量:
,定义决策变量:
| (2-1) |
我们有如下假设:
(1)站点的车辆为同一类型,即车容量相同;
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: