摘 要

Abstract 2

第一章 绪论 3

1.1课题的背景及意义 3

1.2现阶段国内外的发展情况 4

1.3主要研究内容 5

1.4本章小结 5

第二章装箱问题与分组问题 6

2.1装箱问题的定义及原理 6

2.1.1装箱问题的定义及原理 6

2.1.2一维装箱问题的定义及原理 6

2.2分组问题的问题及原理 7

2.3本章小结 8

第三章 遗传算法 9

3.1遗传算法的定义 9

3.2 遗传算法的特点 9

3.2.1遗传算法具有的搜索算法特点 9

3.2.2遗传算法独特的特点 9

3.3遗传算法的基本框架 10

3.4遗传算法的选择、交叉和变异 11

3.4.1 遗传算法的选择 11

3.4.2 遗传算法的交叉 11

3.4.3 遗传算法的变异 12

3.5分组遗传算法 13

3.5.1编码 13

3.5.2交叉 14

3.5.3变异 15

3.5.4反演 15

3.6本章小结 16

第四章 数学建模 17

4.1 目标函数的构建 17

4.2 算法的描述 18

4.3本章小结 22

第五章 仿真实验 23

5.1仿真实验过程 23

5.2仿真实验结果 23

5.2.1仿真实验数据 23

5.2.2仿真实验结论 27

5.3本章小结 28

第六章 结论及展开 29

6.1结论 29

6.2展开 29

致谢 31

参考文献 32

摘要

本文对基于分组遗传算法解决一维装箱问题进行了研究，所得的结果对于船舶制造中如何减少管系装箱所需的箱子数目等相关问题的相关研究与探索具有比较重要的意义。

论文主要探讨了一维装箱问题和分组问题的数学模型（目标函数）和遗传算法的基本原理和基本结构，进而对如何利用分组遗传算法解决一维装箱问题进行了研究、建模和编程，从而借此来对相关问题进行探究。

研究的结果对运用分组遗传算法解决一维装箱问题起到了一定的积极作用，具有一定的意义。

关键词：分组问题，遗传算法，装箱问题，解决问题的编码

Abstract

This paper studies the one-dimensional packing problem based on packet genetic algorithm, and the results are of great significance to the research and exploration of how to reduce the number of boxes needed for piping packing in shipbuilding.

This paper mainly discusses the mathematical model (objective function) of one-dimensional packing problem and grouping problem and the basic principle and structure of genetic algorithm, and then studies, models and programs how to use grouping genetic algorithm to solve one-dimensional packing problem, so as to explore related problems.

The results of this study have played a positive role in solving the one-dimensional packing problem by using the grouping genetic algorithm.

Keywords: grouping problem, genetic algorithm, packing problem, problem solving coding

第一章 绪论

1.1课题的背景及意义

装箱问题 (Bin-Packing Problem)是一个传统的NP-hard问题。装箱问题在我们实际中的生产，生活及工程工业领域广泛的运用，例如任务调度，资源管理，运输设计等诸多方面。第二次世界大战以来，全世界的航运业与造船业有着迅猛的发展，并且航运业与国家的经济军事等方面息息相关，而造船业则是航运业的基础，没有强大的造船业就难以发展和壮大我们的航运业。在当今世界上各海洋强国均投入大量的资金，人力，时间和技术来发展航运业与造船业，以此来在的世界上的经济，军事等各个方面的竞争中取得一席之地。而当今中华人民共和国政府提出的“一带一路”中的“海上丝绸之路”以及“海洋强国”的国策更是在经济和军事两方面依赖造船业和航运业，换句话说就是航运业和造船业是 “一带一路”中的“海上丝绸之路”以及“海洋强国”的国策的基石，没有强大的航运业和造船业就无法完成“海上丝绸之路”以及“海洋强国”这两大与经济和军事密切相关的国策。而在进行完成“海上丝绸之路”和“海洋强国”的国策的过程中的经济发展又会使得更多的资金，人力，时间和技术投入到发展航运业和造船业，使得造船业和航运业近一步得到发展。这个过程如此反复之后形成一个正反馈循环，既能完成实现技术的革新使得造船业和航运业长足的发展，更能使得我国的经济，军事和文化等各个方面在国际上增强竞争力，能够一举两得。而因此在这种情况下航运和造船的技术的创新与成本的控制成为了在航运业和造船业中竞争的关键性因素。船舶制造中需要大量的管路等零件。在船厂管材切割问题中，有一类问题的原管长度各不相同，零件管的长度也各不相同。而将这些零件装箱的效率直接影响船舶制造中的时间成本和经济成本。有效的解决装箱问题可以有效的降低造船的成本，提高产品的竞争力，从而提高我国造船业的竞争力。而提高了造船业的竞争力后也将提高我国航运业的竞争力，从而不仅使得我国的航运业能够更进一步的发展，还能够让我国的经济，军事和文化等各个方面实现长足稳定的发展，从而使得我国能够更好更快的实现“海上丝绸之路”和“海洋强国”的基本国策。

本毕业设计的目的是运用分组遗传算法来解决装箱问题，减少船舶在制造的过程中管系装箱所需的个数从而来减低造船的成本，促进我国造船业和航运业的发展

1.2现阶段国内外的发展情况

装箱问题的研究主要开始于20世纪60年代，最开始是针对切割库存而提出的，切割与装箱问题有着十分密切的联系，他们之间并没有明确的界限[^[1]]。由于目前运筹学完全问题不存在有效时间内求得精确解的算法,装箱问题的求解极为困难,因此,从70~80年代开始,陆续提出的装箱算法都是各种近似算法,如下次适应、首次适应、降序下次适应和调和算法等[^[2]]。

遗传算法（GA）是1975年由J．Holland教授出版的著作《A daptation in Natural and Artificial Systems》中首先提出，是根据达尔文的生物进化理论及遗传变异理论提出的一种基于种群搜索的优化算法，此后遗传算法逐渐为为人所知。而在遗传算法中，现在在国内有杨友林教授提出的“基于模糊 c 均值算法”，李杰教授提出的“最优化理论算法”等算法。

在国外，1992年英国格拉斯哥大学的李耘（Yun Li）指导博士生将基于二进制基因的遗传算法扩展到七进制、十进制、整数、浮点等的基因，以便将遗传算法更有效地应用于模糊参量，系统结构等的直接优化，于1997年开发了可能是世界上最受欢迎的、也是最早之一的遗传/进化算法的网上程序EA_demo，以帮助新手在线交互式了解进化计算的编码和工作原理 ，并在格拉斯哥召开第二届IEE/IEEE遗传算法应用国际会议，于2000年组织了由遗传编程(Genetic Programming)发明人斯坦福的 John Koza 等参加的 EvoNet 研讨会，探索融合GA与GP结构寻优，超越固定结构和数值优化的局限性[^[3]]。

在国内2002年，戴晓明教授等人运用多种群遗传并行进化的思想，对不同种群基于不同的遗传策略，如变异概率，不同的变异算子等方式来搜索变量空间，并利用种群间迁移算子来进行遗传信息交流，以解决经典遗传算法的收敛到局部最优值问题.2004年，赵宏立教授等针对在较大规模组合优化问题上简单遗传算法搜索效率不高的现象，提出了一种用基因块编码的并行遗传算法（Building-block Coded Parallel GA，BCPGA）。2005年，江雷教授等针对并行遗传算法求解TSP问题，探讨了使用弹性策略来维持群体的多样性，使得算法跨过局部收敛的障碍，向全局最优解方向进化。

遗传算法现在已经经过了几十年的发展和进步，已经逐渐被人们所接受和运用，在现实的生活和生产中的各种领域不断的延伸，已经逐步从工程科学延伸到社会科学上。在工程科学上，遗传算法已经逐步成为了一个得到有效解得一个重要工具。

1.3主要研究内容

本文的研究目标是分组遗传算法和装箱问题，对分组遗传算法和装箱问题的基本定义，基本原理，数学模型等问题进行相关的分析、研究和仿真实验，并对其可能产生的问题进行分析。主要内容包括以下几点

（1）简单介绍装箱问题的研究和发展，并且分析装箱问题的基本工作原理。除此之外研究分组遗传算法的定义和基本工作原理。建立一维装箱问题的数学模型[^[4]]，为后面的利用分组遗传算法进行对应的仿真实验做好准备。

（2）介绍分组遗传算法的特定和要求，在C 软件上面编出相关的程序进行仿真研究[^[5]][^[6]]。

（3）完成仿真模拟实验之后，记录下实验的相关数据并且对实验的数据和结果进行分析，得出相应的结论，并对该领域（分组遗传算法和装箱问题）尚需完善的研究方向做出展望。

1.4本章小结

本章初步的教书本文的的研地课题运用分组遗传算法解决装箱问题的三个方面。第一个方面是研究的背景和意义，第二个方面是研究的发展状况，第三个方面是研究的主要内容。第一个方面讲述了装箱问题在实际生活中有重要的作用之外还讲述了在国家发展上面的重要意义。第二章简单介绍了装箱问题遗传算法的发展历史和现状。第三章讲述了研究的主要的内容，以及需要进行的流程和相关的操作，为后面的文章做好了铺垫。

第二章装箱问题与分组问题

2.1装箱问题的定义及原理

2.1.1装箱问题的定义及原理

装箱问题的定义如下：

给定一个有限集O的数字(项的大小)和两个常数C(箱的容量)和N(箱的数量),有可能“包你们项目分成N个箱,即是否存在一个分区的O 放入N或更少的子集,这样元素的子集之和不超过C ? 这种非确定多项式完全决策问题自然会导致与非确定多项式联系优化问题的风险，本文的主体：什么是最好的装箱方法，即上述区分中子集最小的数量是多少。

由于非确定多项式困难，现在还没有已知的多项式时间下运行装箱问题的最优算法。然而，Garey and Johnson引用简单启发式，可以证明它并不比最优箱数上的一个很小的乘数差（但也不比它更好）。这个想法很直接:从一个空箱子开始，将物品一个接一个地拿出来，对于每一个物品，首先搜索迄今为止所使用的箱子，寻找足够大的空间来容纳它们。如果能找到这样的箱，就把项放在那里，如果找不到，就请求一个新的箱。将项目放入找到的第一个可用箱中会产生第一个Fit (FF)启发式。搜索最满的箱子仍然有足够的空间来放置物品，会得到最合适的结果，这似乎是一种更好的启发式，但是，它可以表现得和FF一样好，但速度更慢。

装箱问题按照维度来分一般可以分三种，分别为一维装箱问题、二维装箱问题和三维装箱问题[^[7]]。本文研究的对象是分组遗传算法解决装箱问题，下面主要来解释一维装箱问题的概念、定义和原理。

2.1.2一维装箱问题的定义及原理

一维装箱问题的定义是：只考虑一种因素的装箱问题被称作一维装箱问题，例如只考虑重量或只考虑长度等一个变量因素的装箱问题被称作一维装箱问题。

经典的一维装箱问题可以描述为以下的情况：给定一正数c和一组数L={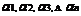}，0lt;≤c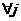，，要寻求一种分拆方法A将L分成一些互不相交的子集B，使得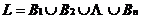，满足条件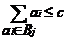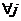，，使得且满足∑ai≤c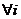，，并使m为能够满足这一要求的最小整数。该问题有着非常广泛的现实背景，如：

(1)客户送来订购单，L代表第i个货件的长度，物品也许会是铜丝、水泥管、光纤、木材等一维线性货物。假如厂家所供应的原材料的标准长度为c，同时满足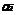≤C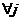，，问如何能以最少量的原材料截出用户所需的物品。

(2)有n个零件需要加工，假定每个零件只需要在一台机器上加工一次即可完成。设第i个零件所需的加工时间为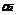，要求所有零件在规定时间c内全部加工完毕，规定所有机器的性能皆相同。问如何能以最少数的机器和人力在规定时间内完成所需加工任务[^[8]]。

2.2分组问题的问题及原理

装箱问题是一个大的问题族群的成员，其中很多问题是在实践中自然产生的，它包括将一组物品的U划分为一组互不相交的子集U i (U)的集合，即

∪ U i = U and

U i ∩ U j = ∅, i≠j.

我们还可以将这些问题看作是将集合U的成员分组为一组或多组(最多为card(U))项，每一项恰好在一组中，即找到这些项的一组。

在大多数这些问题中，并不是所有可能的分组都是允许的。问题的解决方案必须遵守各种硬约束，否则该解决方案是无效的。也就是说，通常一个项不能与其余项的所有可能子集分组。

分组的目标是优化在所有有效分组集上定义的成本函数。以下只是三个例子对于已知的分组问题，分组问题的解必须满足硬约束条件(其中C是任意常数)和代价函数最小化。比如以下的几个例子

问题 硬约束条件 成本

装箱 任何组中小于C的项的大小的和 组的数量

车间布图 任何组中小于C的项的数量 车间总流量

图着色 任何组中没有连接的节点 组的数量

从以上我们可以看出，分组问题的特点是成本函数依赖于组的组成，也就是说，单独采取一个项目是几乎没有意义。分组遗传算法(GGA)是一种针对分组问题的特殊结构进行了大量改进的遗传算法。

2.3本章小结

本章阐述了装箱问题和分组问题的概念、定义和原理，由于本文是着重研究一维装箱问题和分组遗传算法，又着重的阐述和解释了一维装箱问题的概念、定义和原理，为后文的用解决分组遗传算法与一维装箱问题做下了铺垫。

第三章 遗传算法

3.1遗传算法的定义

遗传算法是一种特殊的算法。遗传算法借用了自然界和生物界中生物进化的规律（达尔文的优胜劣汰，适者生存的理论），从而演化而来的一种随机的搜索方式。遗传算法的主要的性质有直接对结构对象进行操作，不存在求导和函数连续性的限定;具有内在的隐并行性和更好的全局寻优能力;采用概率化的寻优方法，能自动获取和指导优化的搜索空间，自适应地调整搜索方向，不需要确定的规则等独特的性质[^[9]]。遗传算法的这些性质已经被人们广泛的运用到各个方面。例如组合优化，机械学习，信号处理等各个方面，是与当今与智能计算中有联系的重要、重点技术。

3.2 遗传算法的特点

3.2.1遗传算法具有的搜索算法特点

遗传算法是一种用来解决搜索问题的通用算法。遗传算法可以适用于各种的通用问题。而搜索算法的共同特点遗传算法也具备。搜索算法的特点有一下几点

1. 首先要组成一组候选解
2. 依据某些适应性条件测算这些候选解的适应度
3. 根据某些特定的适应性条件来测算这些解的适应度
4. 根据测算出的适应度来保留一些候选解，并且同时放弃剩下的候选解
5. 对保留下来的候选解进行某些新的操作，从而生成新的候选解

在遗传算法中，上述的几个特点以一种特殊的方式组合在一起:基于染色体群的并行搜索，带有猜测性质的选择操作、交换操作和突变操作。这种特殊的组合方式将遗传算法与其它搜索算法区别开来[^[10]]。

3.2.2遗传算法独特的特点

遗传算法出了以上这些和其他搜索算法相同的特点外，还具有以下独有的一些特点：

(1)遗传算法从问题解的串集开始搜索，而不是从单个解开始。这是遗传算法与传统优化算法的极大区别。传统优化算法是从单个初始值迭代求最优解的;容易误入局部最优解。遗传算法从串集开始搜索，覆盖面大，利于全局择优。

(2)遗传算法同时处理群体中的多个个体，即对搜索空间中的多个解进行评估，减少了陷入局部最优解的风险，同时算法本身易于实现并行化。

(3)遗传算法基本上不需要搜索空间的知识或其它的辅助信息，而仅用适应度函数值来评估个体，在此基础上进行遗传操作。适应度函数不仅不受连续可微分的约束，而且其定义域可以任意设置。这一特点使得遗传算法的应用范围大范围的扩展。

(4)遗传算法不是采用确定性规则，而是采用概率的变迁规则来指导它的搜索方向。