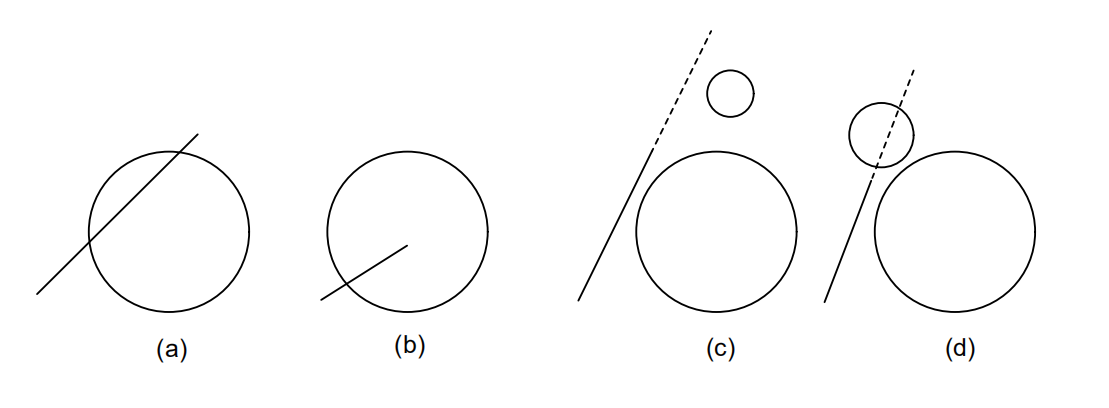摘 要

我国既是传统的陆地大国，也是新兴的海洋大国，在广阔的幅员中拥有着广泛的海上战略利益。经过近年来的发展，我国的海洋事业整体上迈进了历史上的最好发展阶段。随着我国海洋强国战略的推进，水下机器人作为我国海洋事业的重要组成，在军事与民用方面均得到了广泛的关注。在人工智能算法与万物互联的当下发展趋势下，水下机器人作为各类水下作业的新兴载体，有着广泛的应用前景。解决水下机器人路径规划问题是水下机器人技术发展的基础与重点，也是海洋事业发展的重要节点。

本文基于量子粒子群优化算法（Quantum behaved Particle Swarm Optimization, QPSO）提出了水下机器人路径规划的方法。首先，本文明确了目标函数的计算流程。通过构建障碍物模型，将实际复杂的水域环境简化为二维平面图形。定义了节点的搜索方法，为QPSO算法的赋值与节点坐标建立起联系。设立了长度、安全、转角多个成本系数，综合反映生成路径质量。随后，本文介绍了QPSO算法的发展背景，描述了QPSO算法的工作流程，利用标准测试函数检验了QPSO算法的性能。最后，在建立起合理的目标函数与完成QPSO算法代码的基础上，将二者有机结合，通过QPSO算法对目标函数进行优化求解，得到了最优路径，通过对不同方案与地形所产生的最优解进行分析，验证了QPSO算法的性能，掌握了QPSO算法的工作特性，并对未来发展趋势进行了展望。

关键词：水下机器人；路径规划；目标函数分析；量子粒子群算法

Abstract

China is both a traditional land power and a new maritime power with extensive maritime strategic interests. After years of development, China's Marine industry has generally entered the best period of development in history. With the advance of China's Marine power strategy, as an important component of China's Marine cause, Autonomous Underwater Vehicle (AUV) have attracted extensive attention in both military and civil fields. Under the current development trend of artificial intelligence algorithm and the interconnection of everything, AUV, as a new carrier of various underwater operations, has a broad application prospect. Solving the problem of AUV path planning is the basis and focus of the development of AUV technology, and is also an important node of the development of Marine cause.

In this paper, proposes a path planning method for AUV based on Quantum behaved Particle Swarm Optimization (QPSO) algorithm. Firstly, the paper clarifies the calculation flow of the objective function. By constructing the obstacle model, the complex water environment is simplified into a two-dimensional plane figure. The node search method is defined, and the QPSO algorithm assignment is connected with the node coordinates. A number of cost factors, such as length, safety and turning Angle, are set up to comprehensively reflect the quality of the generated path. Then, this paper introduces the development background of QPSO algorithm, describes the work flow of QPSO algorithm, and uses the standard test function to verify the performance of QPSO algorithm. Finally, on the basis of the establishment of a reasonable objective function and the completion of the QPSO algorithm code, the two parts are combined organically. The objective function is optimized by QPSO algorithm, and the optimal path is obtained. By analyzing the optimal solutions generated by different schemes and topography, the performance of QPSO algorithm is verified, the working characteristics of QPSO algorithm are mastered, and the future development trend is forecasted.

Keywords: Autonomous Underwater Vehicle; Path planning; Objective function analysis; Quantum particle swarm optimization

目 录

第1章 绪论 1

1.1目的及意义 1

1.2国内外研究现状 1

1.3研究内容 2

1.4技术路线 3

1.5 论文结构 4

第2章 目标函数的建立与分析 1

2.1障碍物模型的建立 1

2.2障碍物模型的储存 2

2.3路径的建立与可行性判断 2

2.4适应度函数的确定方法 4

第3章 量子行为粒子群算法的背景与仿真分析 1

3.1算法背景 1

3.2算法流程 1

3.3标准函数测试 3

第4章 水下机器人路径规划仿真实验与分析 1

4.1路径规划简介 1

4.2基于QPSO算法的路径规划 2

4.3仿真环境介绍 3

4.4仿真数据与分析 3

第5章 结论与展望 1

5.1全文总结 1

5.2展望 1

参考文献 1

致 谢 1

第1章 绪论

1.1目的及意义

水下机器人在军事武器、国土安全、水文测量、矿产调查、环境监测和海洋研究等领域具有广阔的应用前景，已成为海洋研究的一个重要领域。多年以来，为应对海洋勘探开发项目的挑战，水下机器人的研制工作不断深入^[1]。水下机器人在经过多年的发展之后，已成逐渐成为了西方主要国家发展智能化、现代化海军武器的方向之一^[2]。对于水下机器人而言，其主要工作目标是水下发现目标、辨识目标，并针对目标收集尽可能多的信息或者采集尽可能多的资源^[3]，因此对于精确的运动控制能力具有极大的需求。此外，部分水下机器人需要电池供电，合理规划其作业路径，对于水下机器人降低综合能耗、提升续航范围、拓展应用领域至关重要^[4]。量子粒子群优化算法（Quantum-behaved PSO ,QPSO）是近年来提出的一种智能优化算法，对于求解路径规划问题非常适用。因此，本文基于量子粒子群优化算法，针对水下机器人路径规划方法进行研究。

1.2国内外研究现状

水下机器人（Autonomous Underwater Vehicle）的路径规划问题是指AUV在已知水域环境、存在预设起点与目标点的情况下求出一条可用路径，该路径能避开障碍且满足路程最短、用时最少、耗能最低等最优条件^[5]，称之为最优路径。AUV路径规划由两部分组成:一是基于已知环境信息的全局路径规划;二是基于传感器数据的局部避障规划^[6]。当前国内外用于水下机器人路径规划的经典算法有 算法、算法、神经网络算法等^[7-8]。但是上述经典算法在复杂环境下可能存在计算复杂程度高、耗费时间长的问题。因此进一步提出了群体智能（Swarm Intelligence, SI）算法，如遗传算法^[9]、蚁群算法^[10]、粒子群优化算法^[11]等均属于此类。其中粒子群优化算法（Particle Swarm Optimization Algorithm, PSO）是群体智能算法的一种新型典型代表。PSO算法，即粒子群优化算法，是首先由Kennedy博士和Eberhart博士提出的，这一算法的主要思路起源于对动物群体行为，例如对鸟类的研究^[12]。PSO算法自提出以来，由于其耗费计算资源少、简单易行、参数便于调整等特点，在算法的理论分析、性能改进以及应用等方面取得了相当大的成果。

为了进一步解决PSO算法中受普通粒子限制，不能覆盖整个解空间的问题^[13]，孙俊、方伟、吴小俊等以标准PSO算法为基础，利用量子力学中的相关理论作为背景知识，建立了一种新的PSO算法，即量子行为粒子群优化算法^[14]。目前QPSO算法由于其优良的性能和通用性，受到了国内外研究人员的关注。将该算法应用于水下机器人路径规划问题可以在高效地生成全局最优路径同时做到占用较少的计算资源，相较于PSO算法与遗传算法体现出了优秀的性能^[15]，优化了工作效率，提升了最大续航里程，拓展了应用前景，为水下机器人实现进一步智能化、集群化发展奠定了良好的技术基础^[16]。

1.3研究内容

水下机器人在实际应用中可能会遇到复杂的工作环境，而其通常以电池为能量来源的特性决定了其有限的工作范围。以量子力学相关理论为背景基础，基于QPSO算法，对水下机器人进行合理的路径规划，可以有效地提升其工作性能，通过模拟仿真检验其在复杂环境下的具体性能表现，验证该算法在综合时间消耗、计算资源占用、生成路径质量等方面的性能。具体研究内容及方法如下：

（1）构建目标模型

用粒子来代替实际的水下机器人航迹以建立模型。此处的粒子并非牛顿空间中的运动物体，而是具有动量与能量的量子粒子，通过波函数可以表述出其运动状态。

（2）实现QPSO算法

根据QPSO算法的具体步骤，基于C 语言实现QPSO算法的具体程序。

（3）进行仿真实验

运行上述QPSO算法程序，在构建的仿真环境水域中测试该算法程序，记录、整理程序输出结果，为进一步分析积累可用材料。

（4）总结优化QPSO算法程序

根据QPSO算法程序输出，检验该算法实际性能，分析程序生成路径是否符合预设要求及实际应用情况，并将该算法输出结果分类型进行对比分析，判断算法性能优劣。在上述QPSO算法程序基础上进行总结归纳，探究该算法的应用特点。

图1.1

1.4技术路线

本文基于量子粒子群算法，针对水下机器人路径规划问题进行优化求解，其具体技术路线如下：

（1）建立目标函数的具体计算方式与算法流程。

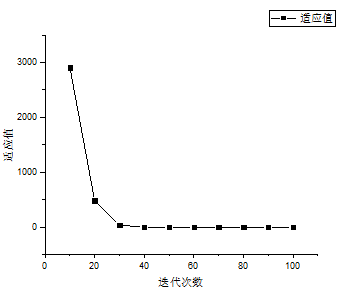
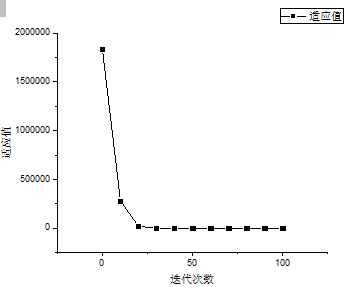
（2）完成QPSO算法代码并调试完成。利用Rosenbrock与Sphere这两个标准测试函数检验QPSO算法的性能。

（3）在建立起合理的目标函数与完成QPSO算法代码调试的基础上，将二者有机结合，通过QPSO算法对目标函数进行优化，得出最佳路径的各节点坐标，通过对QPSO算法最优解进行分析，验证QPSO算法的性能，掌握了QPSO算法路径规划的工作特性。

图1.2

1.5 论文结构

本文分为5章，各章节将按照以下内容进行展开：

第1章：绪论。该段将首先阐述本文的研究内容、研究目的与研究意义，然后将介绍水下机器人路径规划相关研究背景以及国内外研究现状，确立本文的研究目标，最后说明了本文的技术路线。

第2章 目标函数的建立与分析。首先将提出障碍物的处理方式，描述障碍物模型的建立与储存，然后介绍可行路径的多种构造方法，最后确定适应值函数的计算方法，明确目标函数的结构框架。

第3章：量子粒子群优化算法的背景与仿真分析。首先介绍量子粒子群优化算法的诞生历程与应用背景，然后展示量子粒子群优化算法的具体计算方式与循环流程，最后通过使用部分标准测试函数验证量子粒子群优化算法的性能。

第4章：水下机器人路径规划实验仿真与分析。首先介绍路径规划的定义与应用场景，列举当前应用于路径规划的主流算法，引出本文所采用的QPSO算法，然后介绍基于QPSO算法的水下机器人路径规划的基本技术路线，最后声明仿真实验的环境与仿真的结果，并针对性地做出了分析。

第5章：总结与展望。在全文的基础上作出了概括性的总结，总结论文取得的成果，并基于论文推进过程中的感受与收获做出与论文主题相关的反思与展望。

第2章 目标函数的建立与分析

本章首先描述了针对水下环境中障碍物的模型建立，随后介绍了论文中所需的适应度函数的确定方法，并以此为基础，构建了目标函数的整体框架，为算法函数提供了分析、处理的对象。需要提前声明的是，由于水下机器人在工作过程中排除以人工操作为主的部署阶段的下潜过程以及回收阶段的上浮过程，大部分工作时间可以近似地看作为在同一个平面内运行，同时出于简化模型的目的，本文的水下机器人路径规划是在二维平面内进行探讨研究，而后文中的成果与结论亦是建立在此基础之上。

2.1障碍物模型的建立

当以水下机器人为目标进行路径规划时，需要提前获得海洋地形图、障碍物布局，设定好起始位置和目标位置。显然，固定区域的海洋地形图通常不会频繁变化，但其他因素在任务过程中可能会发生动态变化。因此，地形预处理对于后续有效的路径规划至关重要。对于给定的海域，水下机器人能否穿过取决于障碍物的形状和水下机器人自身的机动性能。在路径规划过程中，靠近障碍物在多数情形下可能会获得更有的路径，但同时在另一方面，水下机器人的路径越靠近障碍物，发生碰撞事故的可能性越大。因此，为了水下机器人与障碍物发生碰撞，所有的障碍物都被定义为可以通过一些参数曲线拟合的禁入区域。为了获得更优秀的路径，有时甚至会要求水下机器人在与障碍物保持最小恒定间隙的情况下运行。

将从海洋地形图中获得的几何图形的原始数据与封闭区域的边界点相匹配是模式识别和计算机视觉的基本任务。使用原始模型可以减少和简化数据，从而使后续的处理更快和更简单。在这些原始模型中，圆形模型在医学成像、目标识别、目标检测、工业检测等领域有着广泛的应用。对于当前的问题，所有禁入区域都被建模为圆形。因此，地形预处理的主要任务包括两个步骤。第一步是找出每个岛屿的轮廓，第二步是用最小外接圆拟合上一阶段得到的轮廓点。

综合以上所述，为了简化障碍物模型的建立方法，满足路径规划实时性的要求。本文采用了一种基于最小循环的障碍物建模方法。障碍物可以用其围成的最小外接圆来等价表示。如果需要考虑其他因素，如安全性、测量误差等，可以在最小外接圆的基础上扩展一个安全阈值。

以下为障碍物模型的具体构建步骤:

Step1：将实际海况中的障碍物近似处理成多边形，如果两个或多个障碍物非常接近，则将它们作为一个整体。

Step2：计算多边形的长轴，以长轴为直径，长轴的中点为圆心生成外接圆，逐次迭代，分析外接圆是否为最小外接圆，计算障碍物每个顶点到圆心的距离，取最大值，将最大值的大小与外接的半径进行比较。如果最大值小于外接圆的半径，则圆为最小外接圆，如果最大值大于圆的半径，则继续迭代，直至产生最小外接圆。

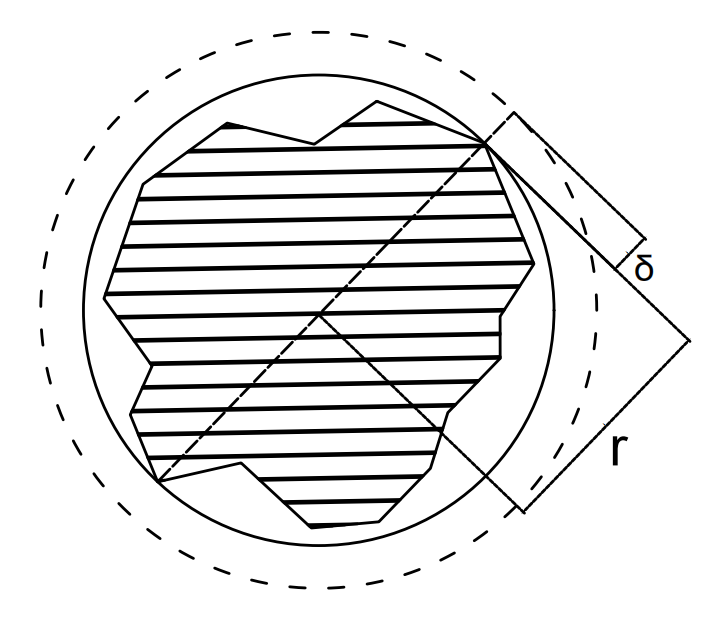Step3：以最小外接圆为基础，向外拓展安全阈值，形成障碍物模型。

图2.1

2.2障碍物模型的储存

通过上述方法完成障碍物模型的建立之后，通过构造体将障碍物模型的相关数据进行储存，以便后续调用。需要储存的信息有：（1）障碍物的等价圆的圆心坐标。（2）障碍物的等价圆的半径r。（3）障碍物的拓展安全阈值。

2.3路径的建立与可行性判断

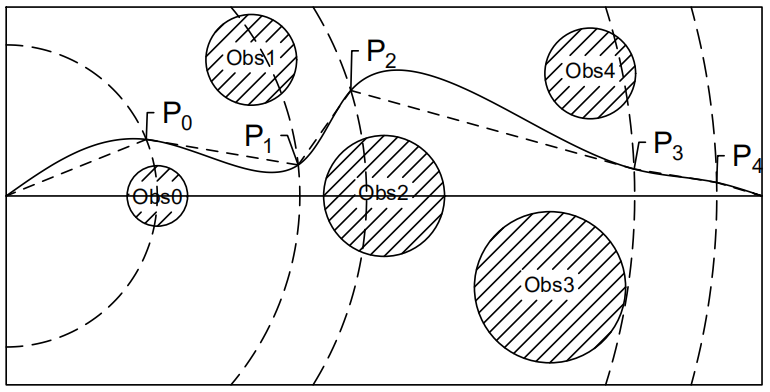
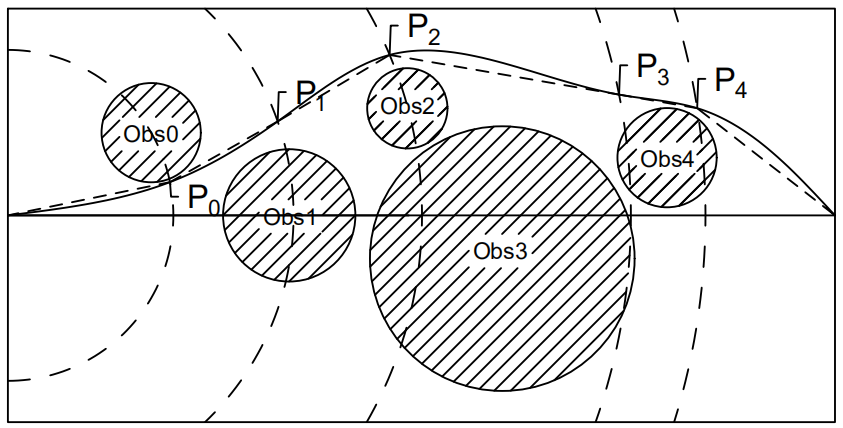
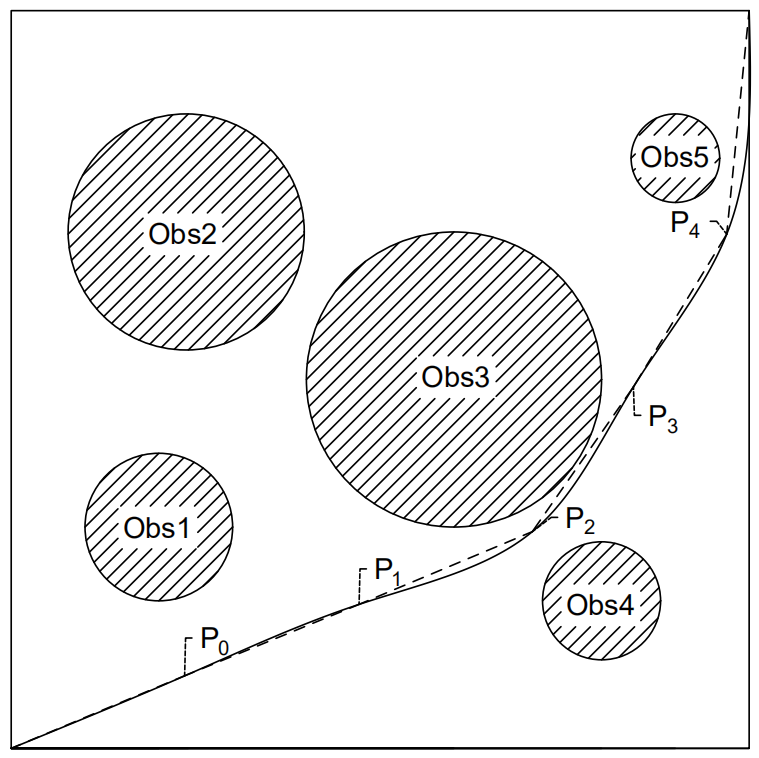
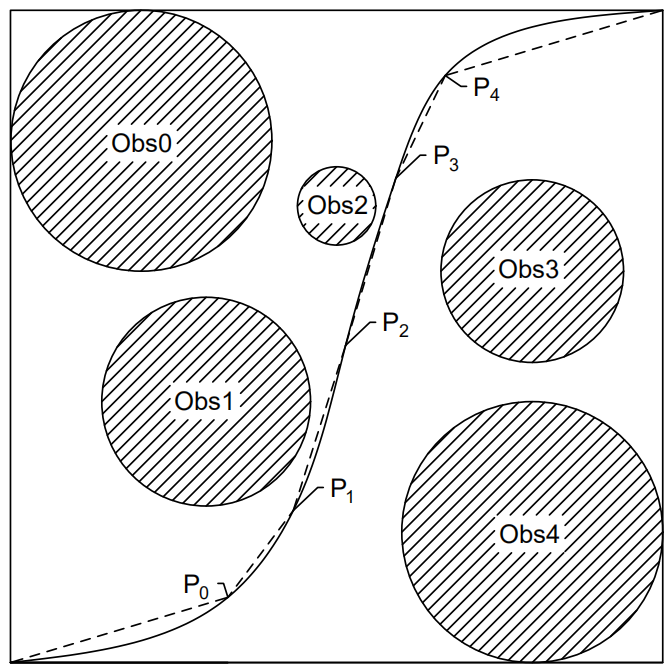
本文采用了QPSO算法进行路径规划，算法中的每一个粒子对应的都是一条单独的路径，粒子的维度可以是障碍物的数量，也可以是根据需要所设定的具体数值。算法所产生的结果是一系列的分支点（Sub-path point），在后文中称之为节点，而算法的最优解则是从起点出发，依次逐个经过各节点最终到达目标点所经过的总路程最短。为了评价算法所产生的每一条路径的优劣程度，即对于目标环境的适应程度，本文将构建适应度函数，但首先需要设计出合理的方案以将QPSO算法迭代过程中所赋予的数值与路径位置对应起来，即需要明确如何用QPSO赋值来产生节点位置坐标。本文分别采用了两种不同的方案以应对不同场景的优化：

（1）方案一：

Step1：以起始位置为原点，在极坐标系下建立障碍物地形图。

Step2：以当前位置为原点，计算原点到下一个障碍物等效圆圆心的极径与极角。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：