基于鲁棒UKF的水下机器人目标跟踪算法毕业论文
2020-02-19 09:02:59
摘 要
我们知道,水下世界错综复杂,而对目标的精确跟踪与否则直接影响工作的成败,该技术无疑是研究的重中之重。如何在误差的影响下尽可能的对目标进行精确跟踪,这正是技术中的核心部分,也正是本文研究的主要目标。本文所研究的基于鲁棒UKF的水下机器人目标跟算法是基于传统无迹卡尔曼滤波器(UKF)的基础上加以改进,传统无迹卡尔曼滤波算法在近几年中广泛应用于精确目标估计中,在工程中展现出了精度高、稳定性好、实现简单等优越性能,而经过改进的鲁棒UKF则更适用于误差波动较大的复杂环境中。本文以数学建模模拟的水下机器人运动模型为目标,分别使用卡尔曼滤波、无迹卡尔曼滤波和鲁棒无迹卡尔曼滤波对其进行分析处理,通过比较他们的处理结果来判断鲁棒UKF的表现,经过实验,结论如下:
1)通过对经典卡尔曼滤波的详细分析,验证了其在处理线性系统量测数据时的有效性,同时也证明了卡尔曼滤波在应对非线性系统时的不足之处;
2)在经典卡尔曼滤波的基础上,引入UT变换使KF转化成可以应对非线性系统的UKF;通过观察实验结果,可以看出UKF在处理非线性系统时相较于传统KF在性能上有着很大的提升,但当测量数据被大量偏差很大的误差值污染时,UKF的性能大大减弱,效果不尽如人意;
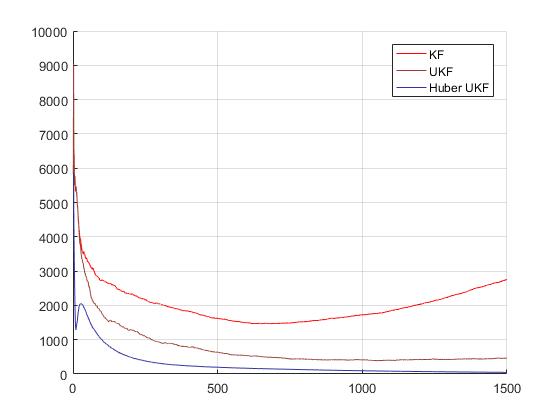
3)同样以实验结果证明了在存在很大的干扰的情况下,Huber_UKF的性能相比前两者有了飞跃性的提升,通过小噪声实验也证明了其在一般情况下依然可以发挥很出色的性能。
关键词:鲁棒无迹卡尔曼滤波,无迹卡尔曼滤波,卡尔曼滤波,非线性,水下机器人
目录
摘要 1
一 绪论 3
1.1研究背景 3
1.2滤波技术概述 3
1.3研究现状 4
1.4本文内容 6
二 滤波算法介绍 7
2.1卡尔曼滤波(KF) 7
2.1.1简介 7
2.1.2数学原理 7
2.1.3实际应用 10
2.1.4小结 15
2.2无痕卡尔曼滤波(UCK) 16
2.2.1简介 16
2.2.2数学原理 16
2.2.3性能比较 17
2.2.4小结 18
2.3鲁棒无痕卡尔曼滤波(Huber_UCK) 18
2.3.1简介 18
2.3.2数学原理 19
2.3.3性能比较 19
2.3.4小结 20
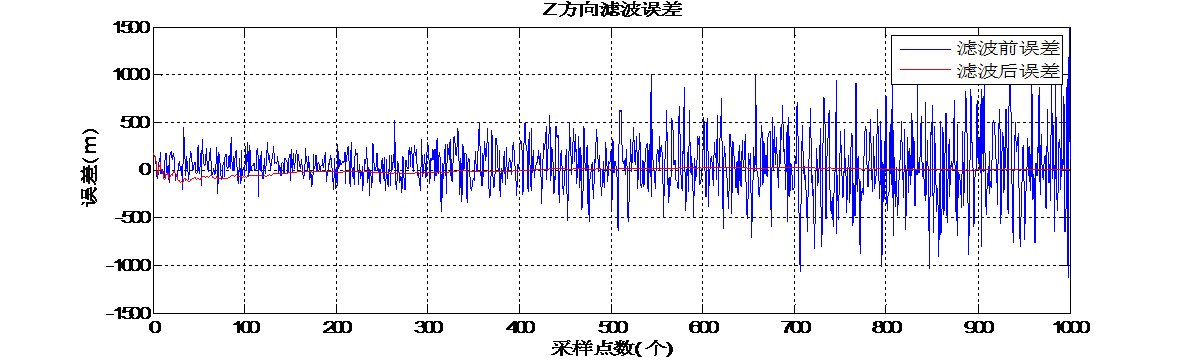
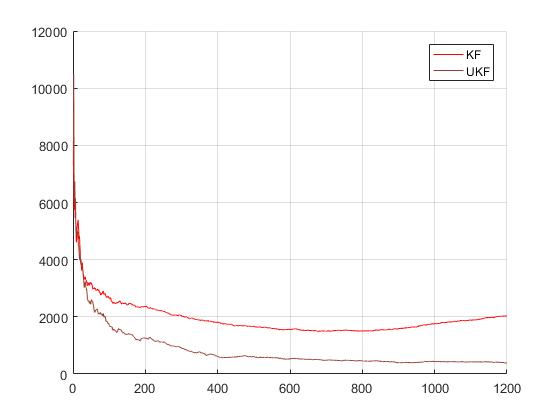
三 仿真实验及结果分析 21
3.1简介 21
3.2条件设定 21
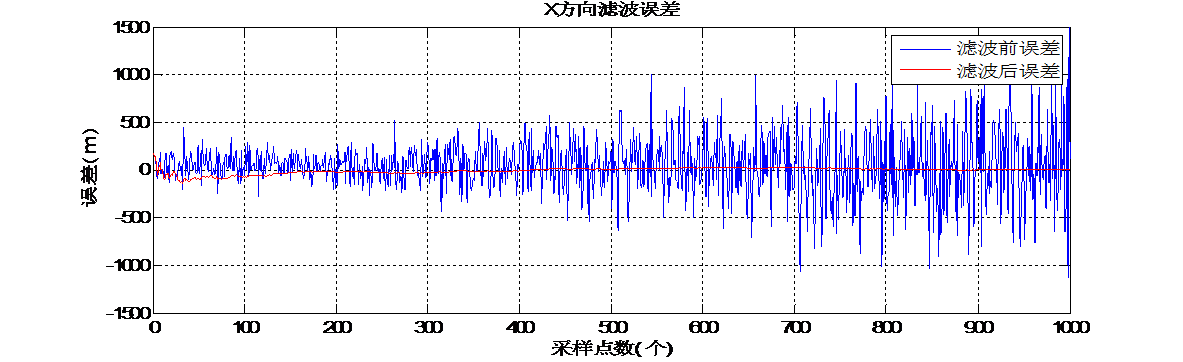
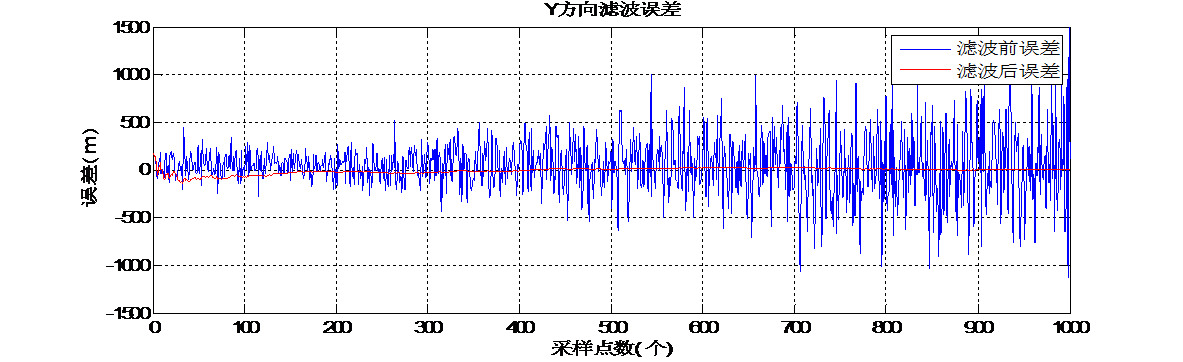
3.3结果比较 22
3.4小结 23
四 总结与展望 24
4.1总结 24
4.2展望 24
后记 25
参考文献 26
附录 27
一 绪论
1.1研究背景
古往今来,人类对海洋资源的探索从未停止,如今,对海洋资源探索已经步入了一个新的阶段,不同于过去仅限于水上航线的开辟与沿岸资源的开发,如今,世界各国在军事、科研与商业等各个领域,对水下世界的探索与开发都有着迫切的需求。不同于以往的探索环境,水下环境十分危险,对工作人员的生命安全造成了重大威胁,在恶劣的环境下,也会有很多人力所不及的情况。因此,水下机器人应运而生,并且随着日益增长的需求逐渐成为国内外科研人员的重点研究对象。在水下机器人所涉及的诸多技术当中,目标跟踪技术作为水下机器人稳定工作的关键技术之一,直接影响着操作精度和机体自身的安全,一直都有着十分明显的研究意义和工程价值。目前,无人水下航行器(unmanned underwater vehicle ,UUV)主要依靠通过UUV对目标有效辐射(例如声辐射和电磁辐射)的检测,来得到目标相对于自身的位置,也就是相对于UUV的连续方位角。但是,传感器所获得的信息,远远不仅来自于目标自身,水下环境恶劣而复杂,声呐因为周围的各类干扰,获得的信息与真实值有很大的误差,以至于很难获得追踪目标的准确信息。除此之外,水温、海水密度和盐度等其他因素对设备的影响,噪声统计特性(平均值和协方差)未知,估计的准确性未知。这些导致UUV的目标跟踪过程中存在着很多的非线性测量,这会给滤波算法带来极大的困难。所以,一个成熟稳定高效的滤波算法对一部UUV来说意义非凡,对UUV的滤波算法的研究有很大的工程意义。
1.2滤波技术概述
通常来讲,传感器采集到的信号往往混杂了很多无关的干扰数据,从混杂的数据中得到需要的信号,就是滤波的目的。滤波的实现则是通过对系统信号进行测量,根据情况使用特定的统计方法对数据进行处理,然后根据特定的估计准则对目标进行估计。滤波算法的种类有很多,为了在工程上能有效运用,对滤波进行优化是必不可少的。我们所说的“优化”就是在诸多滤波算法中,选取最合适的滤波算法。“优化”的思想不仅在现实生活中具有非常重要的意义,而且在工程研究中也大有可为。优化思想也将始终贯穿在本文始终,滤波的终极意义也是要得到最理想的滤波效果。
1795年,法国数学家高斯(Carl K.Gauss)为了研究行星运动的轨迹,提出了轰动一时的最小二乘估计算法,这就是最早的“滤波”。但是,由于该算法在工程实践应用中只满足了测量误差的方差最小,不关心观测信号的统计特性。所以在大部分情况下该滤波方法性能并不尽如人意。但是最小二乘法还是凭借其算法简单、原理简单、收敛性能好的优势在众多工程领域内活跃至今。
滤波技术不管是在导航定位、弹道目标跟踪还是在卫星姿态估计、图像处理、信号处理都是绝对意义上的核心技术,应用极为广泛。可见,滤波技术于我们的日常生活和科学技术息息相关。
滤波的研究自始至终都是曲折坎坷的,因为自然界几乎完全都是非线性的。简单的线性系统是我们对世界的最初的认识,但自然界并非简单的线性系统,而是充满了更为复杂的非线性系统,自然界中非线性系统的情况占了绝大部分。所以我们要清晰的认识到非线性系统才是世界的本质,只有应对线性的系统的方案,在处理现实情况时是远远不够的。从简单到复杂,是人类对世界认知及研究的基本规律,所以研究滤波也是,从简单的线性系统到复杂的非线性系统是滤波研究的必经之路。
根据滤波所适用的系统,研究者通常将其分为线性滤波系统和非线性滤波系统。其中在线性系统中名气最响的无疑是卡尔曼滤波。在非线性系统中,又可以具体分为以下三类:基于函数近似的滤波、基于确定性采样的滤波、基于随机采样的滤波。其中基于函数近似滤波最具有代表性的是拓展卡尔曼滤波;基于确定性采样滤波的代表是无迹卡尔曼滤波;基于随机采样滤波的典型代表是粒子滤波和容积式卡尔曼滤波。
为方便理解,具体如下图:
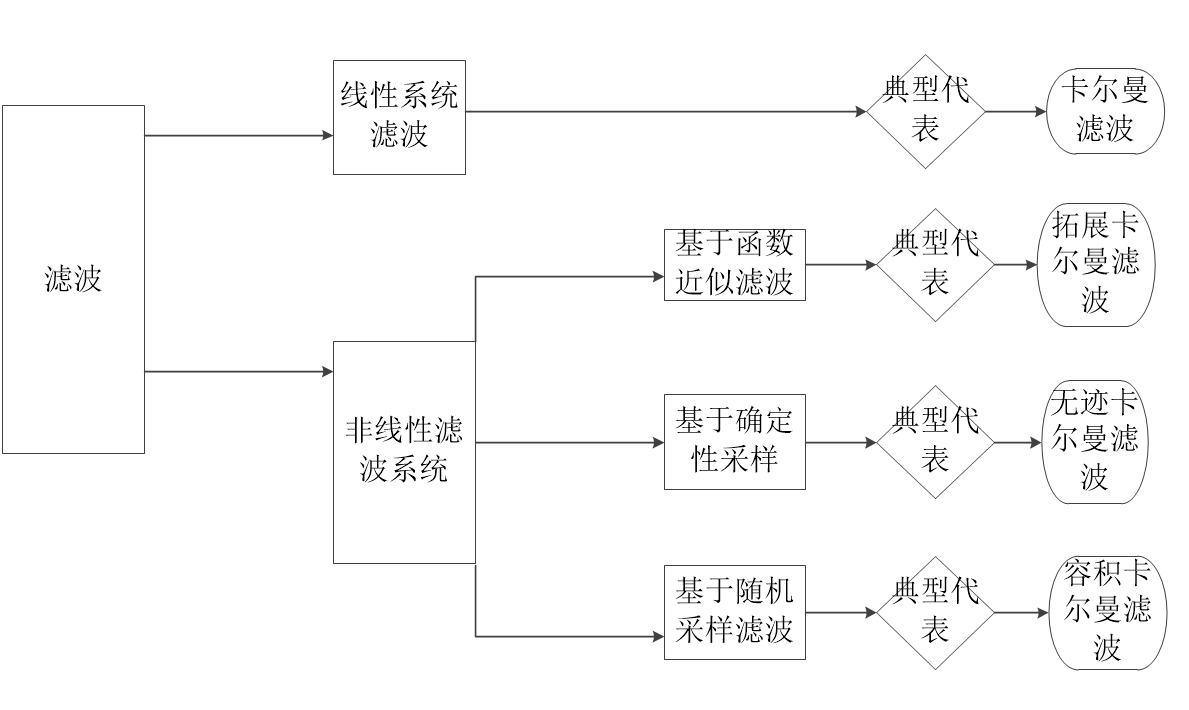
图1-1 滤波分类
1.3研究现状
20世纪40年代左右,美国专家维纳(Wiener)和前苏联科学家科尔曼过洛夫(Kolmogorov)都先后研究出维纳滤波理论。维纳研究维纳滤波的初衷是解决火炮控制问题的,但由于此事关系国家军事机密,直到1949年美国科学家维纳才对外公布维纳滤波原理。由于维纳滤波使用的是频域计划法,因此只能处置安稳的随机进程。维纳滤波的思想是操纵谱分化和平稳随机进程的谱展开式来办理最优滤波的题目的。在频域当中设计维纳滤波器,就无法避免对维纳-霍普方程进行求解,就是计算量大,同时也需要大量的储存空间,是这个方程的一大特点。正是由于维纳滤波原理的这些天然劣势妨碍了它在实际系统中发挥作用,也就意味着维纳滤波器在物理层面上是永远不可能完全实现的。如果我们想在物理层面上得到维纳滤波器,就必须将传递函数的部分分式展开,但遗憾的是维纳滤波是非递推的,而且它的历史数据需要全部储存。正是由于以上种种的天然劣势使得维纳滤波器难以在工程上发挥作用。
20世纪60年代初期,随着技术的发展和革新,尤其是电子信息技术和高速计算机技术的腾飞,人们对性能优越的滤波器的需求愈发迫切。于是,在这样的时代背景下,卡尔曼滤波器横空出世了。它冲破了经典维纳滤波器种种局限,创造性地提出了时域的状态空间方法,并且创造了系统的状态空间和状态变量的观点。状态空间的突出特征是:用状态方程表示动态系统,用量测方程显示状态系统的观测信息,把系统中的状态抽象为一个“点”,再利用希尔伯特(Hilbert)在空间中的射影定理来处理最优状态估计的问题,像这种状态空间方法我们称之为卡尔曼(Kalman)滤波方法,用这种方法建立的状态估计理论我们称它为卡尔曼滤波理论。卡尔曼滤波算法是一种立足于计算机上的,并且易于实时实现的最优滤波算法,由于其数据的存储量小,使得卡尔曼滤波可以从容地处理平稳的随机过程和非平稳过程,这就使卡尔曼滤波算法成功地突破了经典维纳滤波算法的瓶颈。也正是因为这个原因,卡尔曼滤波在机器人、制导、跟踪、石油地震探测、故障诊断等方面大有作为。但是随着时代的发展和计算机技术的进步,卡尔曼滤波对数值的稳定性、实时性、有效性和计算效率的处理结果已经逐渐不能满足人们的需求了。并且由于计算机字长有限的原因,导致了在计算机计算的过程中产生了误差和截断误差积累、传递,最终致使误差方差矩阵的对称正定性消失,造成了数值的发散等严重后果,以上诸问题严重的困扰着无数的工程科研人员。在漫长的科技发展道路上,无数科研人员废寝忘食,苦思冥想的创新卡尔曼滤波,以求改善卡尔曼滤波对于数值处理的稳定性和提高计算效率。目前,研究人员分别提出过平方根滤波、奇异值分解滤波以及UD分解滤波等方法。
自从卡尔曼滤波理论问世以来,如何将其应用于非线性估计问题,这引起了研究人员们的广泛关注。20世纪90年代前期,对于解决卡尔曼滤波的数值稳定性问题,科研人员尝试用分解、补偿算法的方式解决。到了20世纪90年代后期,非线性理论进步神速 ,科研人员不在纠结于以往的泰勒(Taylor)展开式近似的方法转而采用了计算更加简便,精度更好的插值多项式近似的方法,对非线性变换的方法对非线性的模型来变换,走出来传统的线性变换思想。插值法起源于挪威学者Schei,1995年,挪威科学家Schei创造性地提出来用中心差分的方法来改进卡尔曼滤波。也是在同年,牛津大学教授Julier、Uhlmann等人创造性地推出Unscented滤波。随后,来自美国的专家Vander Merwe、Wan等人将Uscented滤波理论进行了创新。这也使得Uscented滤波可以经由一种非线性变换-U变换完成了对误差协方差和非线性状态模型的更新。随着计算机技术的革新和发展,以卡尔曼滤波为基础的现在估计理论已经在航空航天、大地测量、图像处理、故障诊断、控制工程、信息融合等领域作为核心技术在使用。
对于非线性系统状态的精确估计是绝大多数工程领域所面对的难题。目标跟踪方法主要包括扩展卡尔曼滤波器(EKF),最小二乘估计(LSE),Unscented卡尔曼滤波器(UKF)和粒子滤波(Particle Filter,PE)。
目前,应用最广的非线性系统状态估计方法是拓展卡尔曼滤波器(extended Kalman Filter,EKF),传统EKF的原理是非线性系统通过一阶泰勒级数展开式的方式来转化为线性问题,但EKF对于高非线性系统的准确性较差。同时EKF需要计算雅可比矩阵,这就导致了计算系统相当复杂。当非线性函数在通过伪线性变换时,LSE将产生一个有偏差的估计。当UUV执行目标跟踪时,有偏估计对测量的准确性有很大影响。无迹卡尔曼滤波器(Unscented kalman Filter,UKF)通过无迹变换对非线性系统的状态均值和方差进行近似,用构造一组确定的加权样本点的方法来对将要的估计参数进行逼近。这种方法有效地避免了对非线性对象的线性化建模以及雅可比矩阵的计算,是一种直接应用于非线性系统的状态估计的滤波算法。UKF通过一组确定的加权采样点来逼近随机变量的分布函数,避免了求微分问题。相比较于EKF算法,UKF具备的优点,预计会在不久将取代EKF成为常用滤波方法。
1.4本文内容
本文主要探究以卡尔曼滤波为基础的适用于非线性系统的滤波方法。通过对经典卡尔曼滤波和无迹卡尔曼滤波进行严密的数学推导以及仿真实验,提出了基于U变换和Huber M估计理论的Huber_UKF,并验证了其在工程上运用的可行性。
二 滤波算法介绍
2.1卡尔曼滤波(KF)
2.1.1简介
1960年左右,卡尔曼(R.E.Kalman)博士发表了一篇关于动态估计,有着划时代意义的论文:《线性滤波和预测理论的新成果》。这篇震动学术界的文章后来成为了现代控制理论的三个理论支柱之一,在此文中讲述了一种后人称之为卡尔曼滤波的全新的线性滤波和预测理论。该滤波方法的特点是在线性系统的基础上,对输入信号和观测信号经行处理,以求得真实信号。
卡尔曼成功地避免了维纳滤波在应用上的明显问题,提出了离散型的卡尔曼滤波,得到了良好的应用效果。在对雷达信息的处理中,卡尔曼滤波也是最常用的方法之一。它所处理的对象是随机信号,根据接收器收到的观测值作为输入值,按照之前的要求估计量作为滤波的输出值,滤波器的输入和输出是由时间更新和观测更新相关联的,通过状态方程和观测方程得出我们所需要的信号值。
2.1.2数学原理
这一小节我们将针对卡尔曼滤波的流程进行详细描述。卡尔曼滤波的应用流程如下:
第一步,单步预测,根据目标上一时刻的滤波状态来预测当前时刻的目标状态,以下是单步预测计算公式:
( 2-1 ) |
第二步,单步预测误差协方差矩阵:通过状态真值与状态预测值的差值来计算得出协方差矩阵,状态误差的协方差矩阵反映了当前时刻滤波值与真实值的误差,计算公式如下:
( 2-2 ) |
这里的是过程噪声的协方差矩阵。
第三步,滤波增益:以观测信息影响状态估计的权值作为增益值。在测量噪声协方差矩阵增大时,通过使增益矩阵减小,以减小测量噪声对估计值的影响。如果过程噪声协方差矩阵减小时,也减小,则表明状态估计值良好,新的测量值对状态的估计值的矫正影响减弱,增益矩阵也应当变小。
( 2-3 ) |
其中,为测量噪声的协方差矩阵,F和H分别为状态转移矩阵和量测转换矩阵。
第四步,滤波估计:在滤波增益的基础上对量测残差进行加权调整,以得到下一时刻目标的状态估计值:
( 2-4 ) |
第五步,通过滤波误差协方差矩阵来评价滤波性能,以此反映滤波状态值与真实状态之间的误差。该值越小,对目标状态的估计就越准确。
( 2-5 ) |
至此,就是卡尔曼滤波的全过程。通过结合状态方程和量测方程,两者相互配合,卡尔曼滤波就可以精确地估算出目标的运动状态。在多传感器目标跟踪中,其独特的优点则更为显著。以下是卡尔曼滤波的模型讲解。
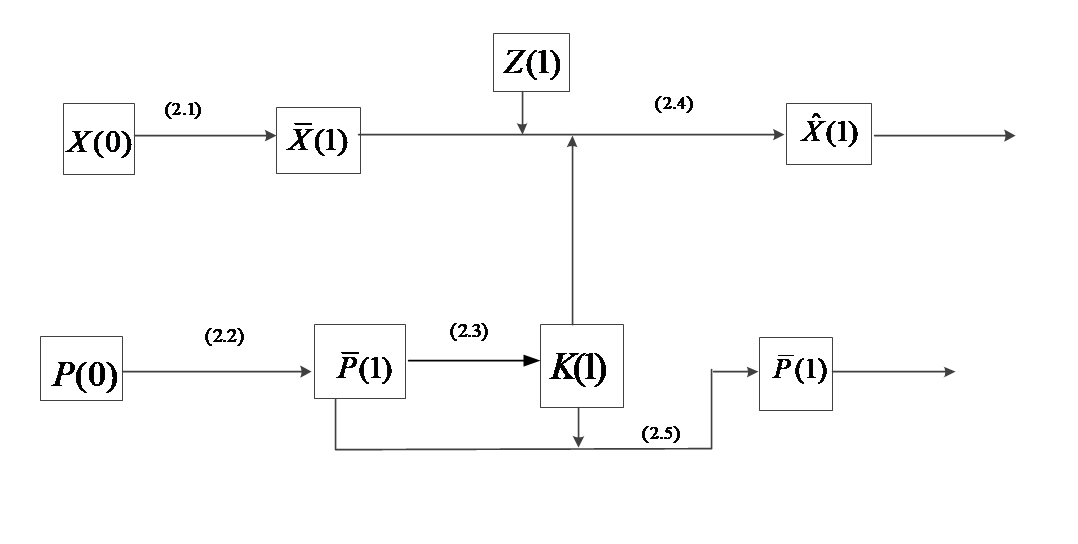
图2-1 卡尔曼滤波计算流程
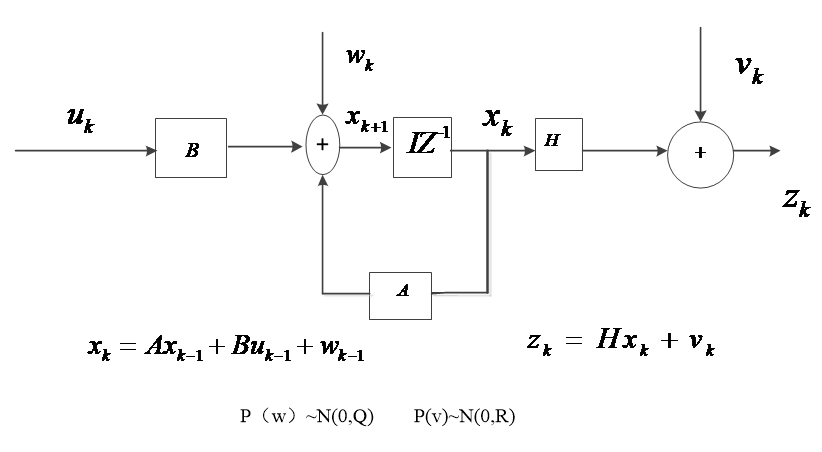
图2-2 滤波流程
激励噪声表示为随机信号w,观测噪声表示为随机信号v,它们是相互独立,正态分布的高斯白噪声。
卡尔曼滤波的目的,就是通过这些已知的信息来估计离散时间进程的状态变量。因为有噪声的存在,我们只能通过估计尽量接近真实值。我们要做的就是要利用已有的信息尽量准确的估算出离散过程的状态变量,从而随时掌握系统的运行状况和变化。

图2-3 迭代示意图
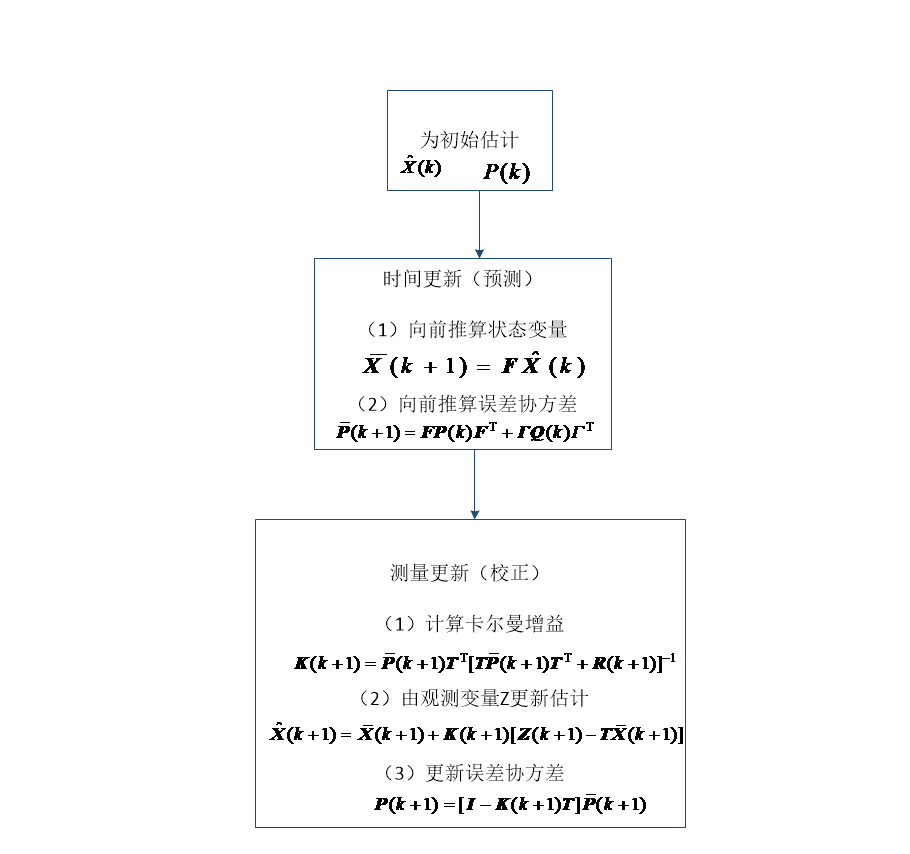
图2-4 具体迭代
2.1.3实际应用
卡尔曼滤波在控制、制导、导航、通讯等现代工程领域有着极为广泛的应用,下面以目标跟踪卡尔曼滤波为例,介绍和分析卡尔曼滤波的实际应用及表现情况。
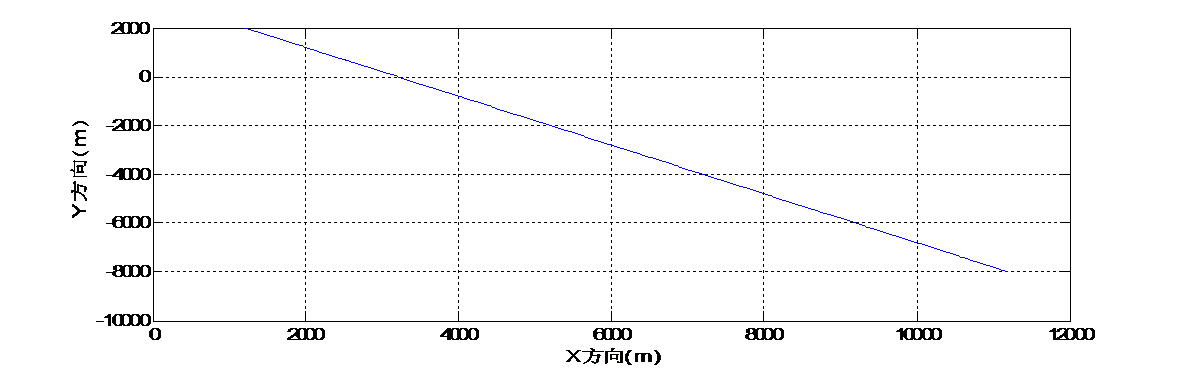
首先,我们先建立一个系统模型,对目标的运动规律进行建模。假设我们的目标在三维空间内匀速直线运动,那么,在离散时间系统下的k 1时刻,目标的运动方程可以表示为:
( 2-6 ) |
这里的,和为时刻目标所在位置,为单位时间间隔。
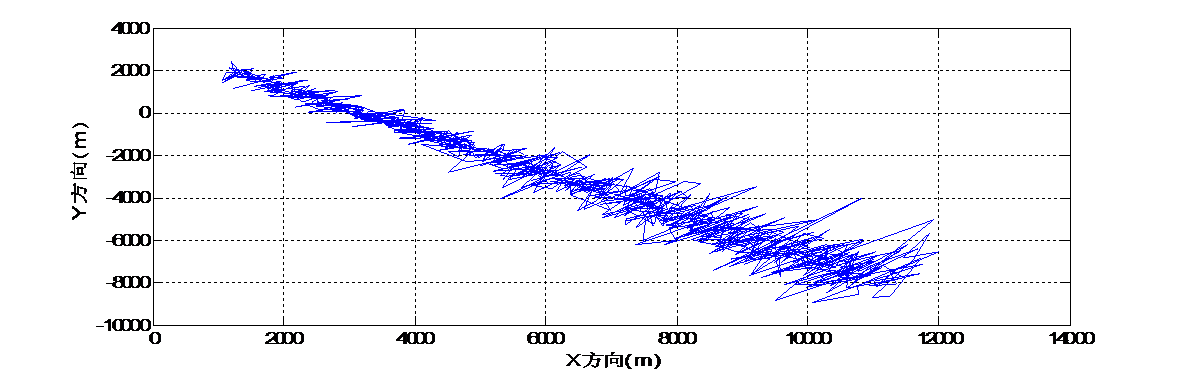
不同于理论模型,在实际情况中,没有影响的情况是不存在的,不可能有绝对的匀速直线运动,速度的小范围波动现象必然会发生。这里我们通过运动方程加入噪声来模拟现实情况,经过噪声干扰后的运动方程为:
( 2-7 ) |
根据运动方程,目标的速度可以表示为:
( 2-8 ) |
以矩阵形式表示为:
( 2-9 ) |
在匀速直线运动模型中,目标的状态方程反映了在不同时刻之间目标状态的关联,运动目标的状态向量表示为,因此目标状态方程表示为:
( 2-10 ) |
其中,为状态转移矩阵,为过程噪声。
接下来,我们来建立量测方程,量测方程是对传感器量测过程的模型假设,量测方程的数据通常是极坐标系数据。因此设传感器在k时刻的量测值为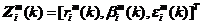 ,其中
,其中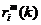 、
、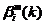 和
和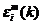 分别为斜距离量测、方位角量测和高低角量测;将其转换到以测量点为坐标原点、以大地为基准平面的直角坐标系(即本文中的参考坐标系)中,则有:
分别为斜距离量测、方位角量测和高低角量测;将其转换到以测量点为坐标原点、以大地为基准平面的直角坐标系(即本文中的参考坐标系)中,则有:
( 2-11 ) |
对其进行泰勒展开,并选择性地忽略高阶项,可以得到:
( 2-12 ) |
这里,为测量转换矩阵。
在没有系统偏差的理想条件下:
( 2-13 ) |
在有系统偏差的条件下:
( 2-14 ) |
其中,为均值为零,量测高斯白噪声向量,,为系统偏差,为系统转移矩阵,形式如下:
( 2-15 ) |
通过该数学模型,就可以得到模拟声呐收集的信号数据。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: