摘 要

在船舶制造和装配过程中，推进轴系的较中一直是一个关键环节，轴系较中的精度直接影响整个动力系统的使用寿命和性能。关于轴系较中的研究一直是一个船舶工业领域的热点。最初的校中方法为直线法，该方法根据轴系的理论中心线，将轴承、法兰等布置成一条直线，但该方法的精度较低。随着计算机技术的发展，一种计算机辅助的船舶轴系较中方法越来越受到人们重视。

以动态校中计算方法为前提，在ANSYS软件基础上，对船舶多支撑轴系负荷进行仿真分析，完善轴系合理校中方法。

本文对上述工作进行了如下研究:

（1）基于ANSYS建立三段中间轴轴系模型，并获取轴承支反力与对应轴承径向高度的样本数据。

（2）对获得的数据分析处理，找寻各轴承的负荷与其变位值之间的变化规律，并通过数据总结出使轴系负荷处于合理范围的变位值大致取值范围。

（3）用ANSYS对主机曲轴建模，通过仿真计算获取变位值及负荷数据，对数据进行分析总结。

关键词：轴系负荷；仿真；曲轴；变位值

abstract

In the process of ship manufacture and assembly, the comparison of propulsion shafting has always been a key link. The accuracy of shafting comparison directly affects the service life and performance of the whole power system. The research on shafting comparison has always been a hot spot in the field of shipbuilding industry. The initial middle method is the straight line method, which arranges bearings and flanges into a straight line according to the theoretical center line of the shafting, but the accuracy of this method is low. With the development of computer technology, more and more attention has been paid to a computer-aided method of ship shafting.

Based on the dynamic comparison method and ANSYS software, the load of multi-support shafting system is simulated and analyzed, and the reasonable comparison method of shafting system is improved.

In this paper, the above work is studied as follows:

(1) Based on ANSYS, a three-stage intermediate shaft shafting model is established, and the sample data of the bearing back force and the corresponding bearing radial height are obtained.

(2) Analyze and process the obtained data, find the change law between the load of each bearing and its displacement value, and summarize the approximate value range of the displacement value that makes the shaft load in a reasonable range through the data.

(3) Model the main crankshaft with ANSYS, and obtain the displacement value and load data to analyze the data.

Key words: Shaft load; simulation; crankshaft; displacement value

目录

一 绪论 1

1.1 研究目的及意义 1

1.2 国内外研究现状分析 1

1.2.1 三弯矩方程算法 2

1.2.2 迁移矩阵法 3

1.2.3 有限元法 4

1.2.4 ANSYS简介 7

1.3 本论文主要工作 7

1.3.1基本内容 7

1.3.2 章节安排 8

二 .船舶轴系模型建立 9

2.1中间轴系模型各项参数 9

2.2 对轴系二维模型的分析 10

2.3 轴系三维模型的建立 11

2.4本章小结 12

三.轴系模型有限元分析 13

3.1网格划分 13

3.2添加约束、载荷及位移 13

3.3数据分析 14

3.4本章小结 19

四.曲轴仿真分析 20

4.1曲轴工作条件 20

4.2曲轴的材料选择 20

4.3柴油机曲轴参数 21

4.4模型分析与假设 22

4.5曲轴模型的建立 22

4.6本章小结 24

五.总结与展望 25

5.1论文总结 25

5.2论文展望 25

致谢 26

参考文献 27

一 绪论

1.1 研究目的及意义

我国为与德国工业4.0^[1]全面对接制定了《中国制造2025》^[2]的行动纲领，旨在利用新兴技术，推动工业智能化，从而构建一个高效节能、绿色环保、环境舒适的人性化工厂。其中，先进的船舶和海洋工程设备是重点发展领域。机舱是船舶的动力源，也是船舶的核心，而轴系项目工程是机舱工作的重中之重。船舶推进轴系统的功能就是将主机的动力传递给螺旋桨，同时将螺旋桨产生的推力传递给船体，从而达到船舶前进的目的^[3]。传动设备、传动轴、支撑部件、艉密封装置，以及其他一些附件

船舶轴系由传动轴、传动设备、支承部件、艉轴密封装置，以及一些其他附件组成。船舶轴系是船舶动力装置的重要组成部分，螺旋桨能否持续正常运转，在很大程度上取决于轴系工作的可靠性。轴系的故障一般有两类：一类是轴的某部分变形、裂缝或折断；另一类是轴承过热后被烧坏^[4]。其原因很复杂，可归纳为两个主要方面：首先是轴系内在的原因，其本身在结构、材料强度等方面存在缺陷；其次是外部原因，轴系在运转中受到异常外力作用^[5]。

为保证轴系长期安全地正常运行，除应保证轴系具有足够的强度和刚度外，还要保证轴系处于合理的状态，以使各个中间轴的应力，以及各轴承上的负荷处在合理的范围之内^[6]。船舶轴系的校中，就是将船舶的理论中心线与实际中心线最大可能的保持一致，或是使其误差足够小，这样船舶轴系承受的额外扭矩与弯曲应力能处于合理范围。好的校中能保证轴系长期在恶劣的条件下工作时不被破坏，保障船舶财产和人员的生命安全，延长船舶推进设备的寿命^[7]。

在计算机高速发展的今天，软件建模也应运而生，成为了计算机时代不可或缺的产物。在轴系合理安装校中前，必要的一步是利用计算机建立轴系简化模型。这样做的目的是让安装工作预先在计算机上开展，这样不仅可以预知轴系负荷情况，还极大的降低了安装过程中造成的不必要的损失^[8]。

1.2 国内外研究现状分析

目前传统轴系校中计算方法有三种：三弯矩方程、迁移矩阵法与有限元法。传递矩阵法编程简单，运算速度快，但适用性差；有限元法计算模型复杂，计算精度高，便于二次开发和其他应用软件的接口，但编程实现相对困难；而三弯矩法介于二者之间，既有传递矩阵简单易于实现的特点，又有利于二次开发，如对艉轴承受力有限元分析，对复杂轴系校中的校中计算、动态校中计算等。但三弯矩方法要具备上述特点，必须进行相应的改进，以满足不同情况轴系校中计算的需要。

1.2.1 三弯矩方程算法

三弯矩法是将轴系视为放置在各个刚性绞支座上的连续梁，而在梁的各截面变化处和集中力作用点都假定有一个虚支座。这样，就可以根据虚支座建立船舶轴系的数学模型。然后用三弯矩法先计算轴系成直线校中状态时，各支座处轴的弯矩、转角及各支座支反力，之后再计算轴系在曲线校中状态（即轴承有变位）时，各轴承的支反力与最佳位移量，也可以计算轴系在各连接法兰处的偏移、开口量和轴承的顶举系数等。

三弯矩算法是一种比较常用的算法，现国内外学者对三弯矩算法均做出了针对不同情形的改进，三弯矩算法得以改进。武汉理工大学的周瑞平^[9]等人对三弯矩方程进行了改进。众所周知，船舶校中分静态与动态校中，而轴系的动态校中更贴近于船舶正常运转状态，为了提高动态校中精度，可将轴系简化后再运用三弯矩方程进行分析。渤海船舶职业学院的李冬梅^[10]等人在基于三弯矩方程下对船舶轴系动态较中进行了研究，她在建立轴系模型前，先将船舶轴系实体进行了简化，简化原则如下：

（1）轴系自重简化：在船舶轴系的简化模型中,为了方便进行校中计算,将中间轴、推力轴承等部件的自重视为均匀分布的载荷。

（2）载荷简化

螺旋桨、连接法兰、飞轮和齿轮等载荷简化为作用于轴径处的集中载荷。

（3）曲轴简化

柴油机曲轴简化为一定直径的光轴,曲轴的载荷简化为均匀载荷。

（4）轴承支点简化

在推进轴系中，主轴上安装的轴承长径比小于1,简化为作用于支点的集中载荷。简化后如图1.1所示

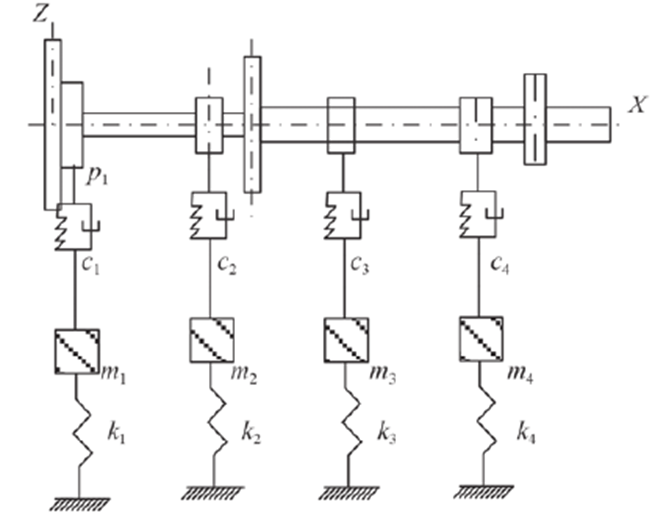
图1.1

由上述简化模型可得到轴系的三弯矩方程：

式中，L_i为相邻两个支撑点的长度，m；M_i为第i个支撑点所受的截面弯矩，N/m；J_i-1为相邻两个支撑点之间的轴截面惯性矩，m³；E_i为轴的弹性模量，N/m。

当第i个支撑为虚支撑时，三弯矩方程变为：

当第n-1个支撑点为虚支撑时，三弯矩方程变为

武汉理工大学的周瑞平等人对三弯矩方程进行了改进：1.计入外加力偶；2.适用于线性均布载荷的三弯矩方程；3.挤入剪切变形影响的三弯矩方程。

实际轴系所受外力不仅作用在垂直平面上，也作用在水平平面方向上，同时也受外加力偶作用。改进后的三弯矩方程与原三弯矩方程相比，不仅可以进行静态校中计算，也可以进行稳定运转状态下的校中计算和动态校中计算。虽然轴系在动态下受力比较复杂，但都可以力的分解，将轴系的实际受力分解到X、Y、Z轴上，直接用改进的三弯矩方程对轴系进行XZ平面上和XY平面上的校中计算。因此改进后的三弯矩方程适用范围更广，能较好地完成各种状态的校中计算。

1.2.2 迁移矩阵法

船舶轴系是由一系列惯性元件和弹性元件连接而成的结构。按照一般结构静力学的线性理论，任意两个相邻截面的状态矢量通过一个线性变换联系着，也就是相邻两截面的状态矢量用一个矩阵相互联系着，变换矩阵把状态矢量从此截面迁移或传递到彼截面，传递矩阵法就是将复杂的弹性系统分解为一些具有简单弹性和运动性质的部件，将这些部件的结合面作为计算截面，根据不同的问题与要求，列出轴系各个结合面处的状态矢量。然后，利用弹性系统各部分之间的传递关系列出传递矩阵，并利用弹性系统各部件之间的边界条件进行求解。

传递矩阵法克服了三弯矩法中把轴承视为刚性支承的不足，从而能更为准确地反映轴承受力与变形的实际情况。此外，传递矩阵法方法简单、编程容易、所占内存少，因此，比三弯矩法更为合理、先进，更适用于船厂进行计算校核。

海军工程大学的刘学伟等人利用传递矩阵法分别建立船舶轴系校中数学模型和弯曲振动数学模型，对船舶轴系设计与布置有一定指导意义^[11]；华中科技大学的董广坤使用传递矩阵法在MATLAB平台上开发了轴系校中计算程序并验证了该软件的计算能力^[12]。

1.2.3 有限元法

有限元法模型比较严格，各种假设条件均接近真实情况，计算精度较高。其计算量大，编程困难。但使用大型通用有限元分析软件ANSYS可以非常方便的进行有限元计算。有限元法是将连续的求解区域离散为一组有限单元，且按一定方式互相联结在一起的单元的组合体，利用在每一个单元内假设的近似函数来分片的表示全求解域上待求的未知函数。

因此，在应用有限元法中的位移法对轴系进行校中计算时，先将呈平面弯曲的轴系划分成为若干个有限的梁段（每一段梁段都是等截面的），称之为一个单元。单元与单元的连接点，称为节点。然后求出每一个单元的刚度矩阵，把全部单元的刚度矩阵分割并按一定规律组合，则可以得到结构（轴系）的刚度矩阵，结合轴系结构受力和约束条件等边界条件，可以求出作用在每一个节点上的集中力，弯矩及转角。

首先建立数学横型：将船舶轴系划分成为若干个有限的梁段（每一段梁段都是等截面的），即一个单元。从轴系中取出任意一个单元e，如图所示的i，i1两节点间的一个单元，其受力状态可由沿Y轴的线位移和绕Z轴的转角来描述。单元受力图如图1.1所示。

y

，

x

图1.1

单元eij两端节点的位移用矩阵表示则为

= ；=

单元eij两端节点的作用力F用矩阵表示为

= ； =

式中y_i，y_j---节点i,j沿y轴的线位移；

φ_i，φ_j---节点i,j绕z轴的角位移；

T_I,T_J---节点i，j上的剪力；

M_I,M_J---节点i，j上的弯矩。

将上述两式合并，则可得到单元的位移及作用力，即：

位移=[y_i φ_i y_j φ_j]^T；

作用力=[T_i M_i T_j M_j]^T。

较中计算时，轴系是在弹性范围内变形，作用力与变形之间呈线性关系，所以可以写为

=

上式中[K^e]为单元刚度矩阵，其性质和弹簧的弹性系数k一样，他表示单元体抵抗外力，使其变形的能力。对于仅仅收到平面弯曲的力系，其位移矩阵为：

=

式中：E—材料的弹性模量

G—材料的剪切弹性模量

I—单元对Z轴的惯性矩

l—单元的长度

按上述方法可以一次求出每一个单元的刚度矩阵，把全部单元的刚度矩阵分割并按一定规律组合，则可得到轴系的刚度矩阵。

位移法在轴系较中计算中的应用：

如上所述，应用位移法应该先求解出各个节点上的位移，再按照位移求出指定截面上的剪力、弯矩及轴承载荷。为此，应该按照轴系校中的约束条件对结构刚度矩阵 [K]进行处理，才可以进行求解。约束条件是指对结构（轴系）的某些节点的位移进行必要的限制。如直线校中时，应使各个轴承沿Y方向的位移为零。按照这种方法对矩阵[K]进行处理，然后就可以求解出各个截面的挠度及转角，从而求出各个截面的剪力、弯矩和各个轴承的负荷。

上述式求解轴系直线校中式的有关参数。当轴系合理校中时，轴系各轴承沿Y轴方向产生位移，这时则按照各轴承的合理位移值为约束条件对[K]进行处理。从而求出轴系合理校中时的制定轴截面的挠度，转角，剪力、弯矩及轴承负荷

当然，有限元法应用需要满足必要的先决条件，主要是三条不可或缺的假设：连续性假设、均匀性假设、各向同性假设。

合理校中的计算是一个优化过程，在计算过程中不仅要考虑轴承、轴段、主机等的要求，还要考虑不同的工况。由于轴系结构的刚度矩阵的生成是一个十分复杂的过程，需要大量的数学计算，不适合工厂工人师傅学习和操作。所以，在按有限元法进行轴系校中计算时，利用ANSYS软件中自动生成刚度矩阵的功能，快速，准确，方便的将轴系结构的刚度矩阵生成并解出结果。而且用ANSYS编制的有限元法程序可以直观的在窗口下生成三维图像，有利于船厂现场施工人员对轴系校中过程中，对轴系的各个截面的参数进行修正和调试。

1.2.4 ANSYS简介

ANSYS软件是融结构，流体，电场，磁场，声场分析等于一体的大型通用有限元软件。从1971年的2.0版本到今天的7.0版本，ANSYS从界面到分析功能等各个方面都有较大的改进。它由世界上最大的有限元分析软件公司之一的美国ANSYS公司开发，能与多数建模软件接口（例如：Pro/EngineerNASTAN,AIgor，I-EAS，UG，SoIid Works，lnventor等）。实现数据的共享和交换，是现代产品设计中的高级CAD工具之一。

ANSYS也是目前世界范围内增长最快的CAE软件，是迄今为止世界范围内唯一通过ISO9001质量认证的分析设计类软件，是经过美国机械工程师协会(ASNME)，美国国家核安全局(NQA)及近20种专业技术协会认证的标准分析软件。在中国，它是第一个通过中国压力容器标准化技术委员会认证，并在17个部委推广使用的分析软件。

ANSYS分析功能简述如下：

（1）ANSYS热分析主要用来计算一个系统或部件的温度分布及其他物理参数（热量的获取或损失热梯度，热流密度等），根据温度场性质的不同，热分析可分为稳态热分析和瞬态热分析两类。

（2）ANSYS电磁分析中考虑的物理量是电场强磁通密度，磁场密度，磁力局，磁力，阻抗，电感，涡流，能耗及磁通量泄漏等等。

结构分析是有限元分析方法最常用的一个应用领域。根据力学性质的不同，ANSYS的结构分析可以分为静力分析，动力学分析（模态分析，谐响应分析，瞬态动力学分析，谱分析）、非线性分析（几何非线性分析，材料非线性分析，状态非线性分析），优化设计，可靠性分析等几类。

一般来讲，ANSYS分析的基本过程可以分为以下几步：