具有角点的轴对称柱对称拉普拉斯方程的闸函数研究毕业论文
2020-02-19 09:57:16
摘 要
拉普拉斯方程是经典的椭圆型偏微分方程, 在一般光滑区域解的存在性已经有了相当充分的研究. 然而对于具有角点的区域, 研究一般需要使用引入闸函数方法. 本论文将对二维和三维柱对称具有角点的区域, 研究其闸函数的存在性和边界正则性问题. 本文首先通过平均值性质, 基本解和极大值原理回顾了调和函数的基本性质. 在此基础上, 对于一般区域, 通过引入佩龙方法, 研究拉普拉斯方程的狄利克雷边值问题. 在研究边界性质的过程中引入了闸函数的概念. 对于二维具有角点的区域, 构造了满足外球条件的闸函数和一类不光滑区域的角点的闸函数. 在此基础上, 对于一类三维柱对称区域构造了合适的闸函数. 并利用闸函数, 研究了调和函数的边界梯度估计. 本文通过研究不同区域闸函数的构造, 加深了对于一般区域中拉普拉斯方程解的认识, 将为椭圆型方程后续研究提供理论支持.
关键词: 调和函数; 闸函数; 拉普拉斯方程; 二维; 三维柱对称
Abstract
Laplacian equation is a typical elliptic partial differential equation, and the existence of solutions in general smooth regions has been well studied. But for regions with corners, the existence is not clear. In this paper, the existence and boundary regularity of barrier functions for corner regions with 2 dimensional and 3 dimensional axisymmetric symmetric domains are studied. First, we studied the properties of harmonic functions by means of mean value properties, fundamental solutions and maximum principles. For the Dirichlet problem of Laplace equation, the Perron method was employed. To consider the boundary property, the barrier function is introduced. For the 2 dimensional case, we construct the barrier functions satisfying the outer sphere conditions and the corner functions of a class of non-smooth regions. Then, we extend the result to the 3 dimensional axisymmetric symmetric case. And, we obtain the gradient estimation of the boundary of harmonic function by using barrier functions. The study on barrier functions is deeper the understanding on the solutions of Laplace equation in general smooth regions, and provide the supports for the further study on the general elliptic partial differential equation.
Key word: Harmonic function; barrier function; Laplace equation; 2 dimensional; 3 dimensional axisymmetric symmetric
目录
第1章 绪论 1
1.1研究背景及意义 1
1.2研究前景 1
1.3研究内容及方法 2
1.4 小结 2
第2章 调和函数的性质 4
2.1概要 4
2.2平均值性质 4
2.3 基本解 12
2.4 极大值原理 20
2.5小结 24
第3章 佩龙方法 25
3.1概要 25
3.2 佩龙方法简介 25
3.3边界梯度估计 31
3.4小结 33
第4章 闸函数 34
4.1概要 34
4.2二维情况 34
4.3三维柱对称情况 36
4.4小结 38
第5章 总结 39
参考文献 40
致谢 42
第1章 绪论
1.1研究背景及意义
1900年, 著名的数学家希尔伯特在巴黎国际数学家大会提出了23个最重要的问题供20世纪的数学家们去研究, 这就是著名的“希尔伯特23个问题”. 其中有3个问题(第19, 20, 23问题)与偏微分方程有关. 自此以后, 偏微分方程特别是椭圆型方程有关研究取得了奠基性的成果和突破性的发展[1].
物理上一些最著名的模型都可以归结为椭圆型方程. 例如牛顿万有引力的位势, 平衡态热方程温度都满足拉普拉斯方程. 拉普拉斯方程作为经典的椭圆型偏微分方程也是最重要的椭圆型偏微分方程. 因为拉普拉斯方程蕴含了椭圆型方程的最基本的性质. 在一般光滑区域解的存在性已经有了相当充分的研究, 例如: 对于拉普拉斯方程解狄利克雷问题解存在性问题, 已有了相当充分的研究, 例如: 在方形区域中, 可以利用分离变量法将解表示出来; 利用泊松积分公式可以讨论一些球形区域的情况. 但是对于具有角点区域的研究比较少[2].
传统的方法难以处理具有角点区域的拉普拉斯方程, 本文采用佩龙方法来研究上述的拉普拉斯方程. 佩龙方法虽然提供了区域内部调和函数的存在性, 但没有对其边界性质提供任何信息. 因此, 为了研究调和函数的边界性质, 则需要构造出角点的闸函数. 闸函数的概念最早由勒贝格引进. 通过研究闸函数解的存在性和边界的正则性, 有助于研究拉普拉斯方程的边界性质, 从而更好的解决满足该类型的拉普拉斯方程的物理问题. 将具体的物理问题转化为偏微分方程, 再通过对方程的求解, 可以对所描述的物理现象有更加清晰和精细的认识[3].
1.2研究前景
最近几十年椭圆型偏微分方程有了很大的发展, 这些成果大部分都总结在吉尔巴格和特鲁丁格写的《二阶椭圆型方程》书中而具有角点的区域的研究却非常的少. 然而具有角点区域的椭圆型方程在现实的世界中却非常的常见, 例如空气流体力学中, 飞机机头处空气流动的情况. 本文主要研究二维和三维柱对称的角点区域并构造出角点的闸函数. 拓展了椭圆型方程在物理中的应用, 为求解拉普拉斯方程提供了一种新的方法. 同时, 也提供了一种新的方法去研究不可压缩的欧拉方程[4].
1.3研究内容及方法
首先, 定义一个函数的平均值性质. 用平均值性质来研究调和函数并且证明了函数满足平均值性质和调和函数之间是等价的关系. 利用了平均值性质给出了调和函数的内部梯度估计并证明了哈纳克不等式. 接着利用基本解的方法研究调和函数. 通过构造出格林函数来求解泊松方程的第一边值问题. 根据前面的平均值性质已经知道调和函数的极值只能在边界达到. 于是推广到下调和函数, 利用了极大值原理的方法来研究调和函数. 证明了两个极大值原理(强极大值原理和弱极大值原理), 同时利用了极大值原理给出了调和函数的内部梯度估计和哈纳克不等式新的证明[5].
根据拉普拉斯方程(对于带角点的轴对称)构造下调和函数并证明下调和函数的极值原理. 定义 下调和函数: 设
下调和函数: 设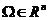 ,
,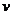 是
是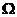 上的连续函数, 若任意的球
上的连续函数, 若任意的球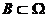 和任意调和函数
和任意调和函数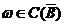 , 如果在
, 如果在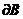 上
上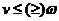 , 那么在
, 那么在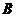 内都有
内都有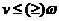 . 从已有的下调和函数构造出它的调和提升函数并且证明该调和提升函数是下调和的. 接着定义一个下调和函数集, 令
. 从已有的下调和函数构造出它的调和提升函数并且证明该调和提升函数是下调和的. 接着定义一个下调和函数集, 令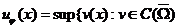 在
在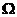 上是下调和函数且在
上是下调和函数且在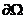 上
上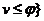 , 证明
, 证明 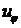 在
在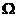 的内是调和函数[6]. 佩龙方法给出了区域内部调和函数的存在性, 但没有提供调和函数的边界性质. 本文利用闸函数研究狄利克雷问题的边界情况, 并证明当
的内是调和函数[6]. 佩龙方法给出了区域内部调和函数的存在性, 但没有提供调和函数的边界性质. 本文利用闸函数研究狄利克雷问题的边界情况, 并证明当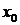 是正则点时,
是正则点时,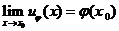 .
.
正则点是边界的几何结构所决定的, 即闸函数的存在依赖于边界的几何性[17]. 当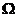
在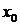 处满足外球条件, 则闸函数可以定义为
处满足外球条件, 则闸函数可以定义为
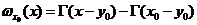 ,
,
对于任意的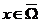 . 其中
. 其中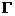 是拉普拉斯方程的基本解. 对于不满足外球条件的角点, 利用极坐标变换, 将该角点满足边界非负的局部调和函数求出. 将此调和函数作为该角点的闸函数.
是拉普拉斯方程的基本解. 对于不满足外球条件的角点, 利用极坐标变换, 将该角点满足边界非负的局部调和函数求出. 将此调和函数作为该角点的闸函数.
1.4 小结
本文主要利用佩龙方法来研究拉普拉斯方程的狄利克雷边值问题. 第2章主要研究调和函数的平均值性质, 基本解和极大值原理并分别利用平均值性质和极大值原理得到调和函数的内部梯度估计和哈纳克不等式. 第3章主要利用佩龙方法来研究调和函数的存在性并用闸函数来研究调和函数边界的正则性. 第4章主要提供了两种不同的构造闸函数的方法并构造出了两种类型区域的闸函数. 第5章总结对于相关情况构造的闸函数, 并对后续研究进行了展望.
第2章 调和函数的性质
2.1概要
在椭圆方程理论中, 调和函数基本性质是最重要的性质, 在某些方面反映了一般椭圆方程解的特质. 本章主要研究调和函数的性质和由这一性质派生的结论, 调和函数由格林函数积分表达式决定的性质以及下调和函数的极值原理.
2.2平均值性质
定义2.2.1 设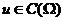 定义
定义
(1) 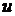 满足第一平均值性质, 若
满足第一平均值性质, 若
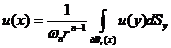 , 对于任意
, 对于任意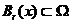 ,
,
(2) 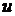 满足第二平均值性质, 若
满足第二平均值性质, 若
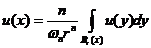 , 对于任意
, 对于任意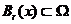 ,
,
这里的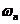 表示
表示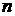 维欧氏空间中单位球面的面积.
维欧氏空间中单位球面的面积.
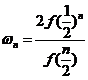 , 其中
, 其中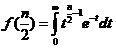 .
.
注2.2.2. 这两个定义是等价的. 事实上, 如果把(1)写成下列形式
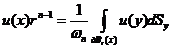 ,
,
可以通过积分得到(2). 如果把(2)写成下列形式
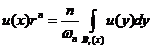 ,
,
可以通过微分得到(1).
注2.2.3. 可以得到平均值的如下等价形式:
(1) 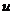 满足第一平均值性质, 若
满足第一平均值性质, 若
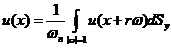 , 对于任意
, 对于任意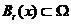 ;
;
(2) 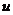 满足第二平均值性质, 若
满足第二平均值性质, 若
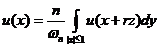 , 对于任意
, 对于任意 .
.
注2.2.4 事实上满足平均值性质的函数一定是连续函数.
定理2.2.5 设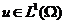 且满足平均值性质, 则
且满足平均值性质, 则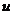 是连续的函数.
是连续的函数.
证明:取任意的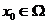 , 对于任意的
, 对于任意的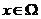 得到
得到
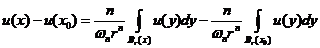
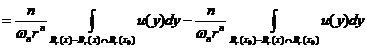 .
.
当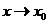 ,
, 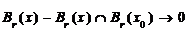 ,
, 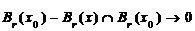 .
.
于是, 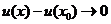 . 因此,
. 因此, 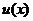 是连续函数. □
是连续函数. □
现在证明满足平均值性质的函数的极大值原理.
命题2.2.6 若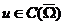 在
在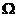 上满足平均值性质, 那么
上满足平均值性质, 那么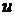 要么在边界取得最大最小值, 要么是个常数.
要么在边界取得最大最小值, 要么是个常数.
证明: 只证明在边界取得最大值的情况. 设
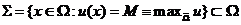 .
.
显然, 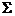 是相对闭集. 接下来证明
是相对闭集. 接下来证明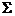 是开集. 对任意的
是开集. 对任意的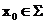 , 取
, 取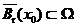 ,
, 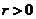 . 通过平均值性质, 得到
. 通过平均值性质, 得到
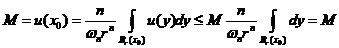 .
.
这表明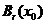 上
上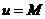 . 于是
. 于是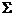 在上
在上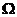 既是开集又是闭集. 由开集和闭集的性质得到
既是开集又是闭集. 由开集和闭集的性质得到 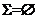 或
或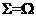 . 当
. 当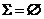 时,
时, 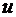 在边界取得最大值; 当
在边界取得最大值; 当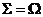 时,
时, 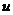 是一个常数. □
是一个常数. □
定义2.2.7 设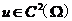 . 若在
. 若在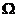 上
上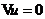 , 则称
, 则称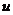 是调和函数.
是调和函数.




