摘 要

在科学发展迅猛的当今社会，流体已经成为人们研究的重要对象。基于流体宏观控制方程－Navier-Stokes方程，人们建立了研究流体的各种数值算法，但这种从宏观控制方程出发的研究途径，在当今科学生产需要下遇到了瓶颈，在有些情况下，并不能得到良好的模拟结果。最近几十年来，从微观角度出发，以Boltzmann方程为核心的格子Boltzmann方法（Lattice Boltzmann Method, LBM）作为一种新兴的介观方法迅速发展起来，并在诸多领域取得了成功。然而这种方法在等温流动下能取得令人满意的结果，但应用到非等温流动，就会出现重重困难。尽管近年来，描述非等温流动的各种LBM也相继被提出，但是标准LBM仅能应用于均匀网格，对复杂边界缺乏良好的适应性。针对该问题，一种基于有限体积框架的格子Boltzmann方法（FVLBM）被提出，并受到了研究人员的关注。气体动理论格式（GKS）是另外一种基于玻尔兹曼方程的有限体积形式的介观方法，它可以直接针对宏观控制方程求解，利用BGK方程的形式解，构造单元界面上的分布函数，巧妙地将BGK方程中的碰撞与对流两个过程结合在一起。整个格式的计算中，流场信息只需要通过宏观守恒量加以记录和更新，此种方法能很好解决非等温流动问题。为尝试解决非等温流动以及复杂边界等问题，本文提出了一种格子Boltzmann方法和气体动理论BGK格式混合数值算法。主要包括工作如下：

（1）选取D2Q9的模型，基于二维的三角形网格，建立有限体积格子Boltzmann方法，模拟不可压缩流动的速度场；

（2）建立气体动理论Boltzmann-BGK模型，构造温度T的GKS；

（3）基于本文提出的方法，测试几个算例，检验此方法的实用性。

关键字：格子Boltzmann方法；非等温流动；FVLBM；气体动理论格式；混合数值算法

Abstract

Fluid has become an important object of research in rapid development today's society . Based on the Navier-Stokes equation, various numerical algorithms for fluid research have been established. However, the research approach based on the macro-control equation meets the bottleneck in the need of scientific production nowadays, and in some cases, satisfactory simulation results can not be obtained. Lattice Boltzmann Method (LBM), with Boltzmann equation as its core, has been developed rapidly in recent decades as a new mesoscopic method and has achieved success in many fields. However, this method can achieve satisfactory results under isothermal flow, but when applied to non-isothermal flow, there will be many difficulties. Although various kinds of LBM describing non-isothermal flow have been proposed in recent years, the standard LBM can only be applied to uniform grids and lacks good adaptability to complex boundary conditions. To solve this problem, a lattice Boltzmann method based on finite volume frame (FVLBM) has been proposed and attracted the attention of researchers. The gas dynamic theory scheme (GKS) is another finite volume mesoscopic method based on Boltzmann equation. It can directly solve the macroscopic control equation. By using the formal solution of BGK equation, the distribution function on the interface of the cell is constructed, and the collision and convection processes in BGK equation are skillfully combined. In the calculation of the whole scheme, the flow field information only needs to be recorded and updated by macroscopic conservative quantities. This method can solve the problem of non-isothermal flow very well. In order to try to solve the problems of non-isothermal flow and complex boundary, a hybrid numerical algorithm based on lattice Boltzmann method and gas dynamic theory BGK scheme is proposed in this article. The main work is as follows:

(1) A finite volume lattice Boltzmann method is established to simulate the velocity field of incompressible flow based on the D2Q9 model and two-dimensional triangular mesh.

(2) The Boltzmann-BGK model of gas dynamics theory is established, and the GKS of temperature T is constructed.

(3) Based on the method proposed in this paper, several examples are tested to verify the practicability of this method.

Key words: Lattice Boltzmann Method; non-isothermal flow; FVLBM; GKS; hybrid numerical algorithm

目 录

摘 要 I

Abstract II

第1章 绪论 1

1.1 研究背景 ……………………………………………..………………………. 1

1.2 目的及意义 2

1.3 有限体积LBM与GKS简介 2

1.3.1 有限体积LBM 2

1.3.2 GKS概述 3

1.4 本文研究内容及创新点 3

1.4.1 研究内容 3

1.4.2 本文创新点 4

第2章 非等温流动的FVLBM与GKS混合算法 5

2.1 求解速度场的FVLBM算法 5

2.1.1 格子Boltzmann方程的数值离散 5

2.1.2 网格边界中心的分布函数重构 6

2.1.3 单元中心分布函数梯度计算 6

2.1.4 边界处理 7

2.2求解温度场的GKS算法 9

2.2.1 C-E展开分析 9

2.2.2 构造温度T的GKS 9

2.2.3 网格边界中心分布函数计算 12

2.2.4 边界处理 15

第3章 数值计算结果与分析 16

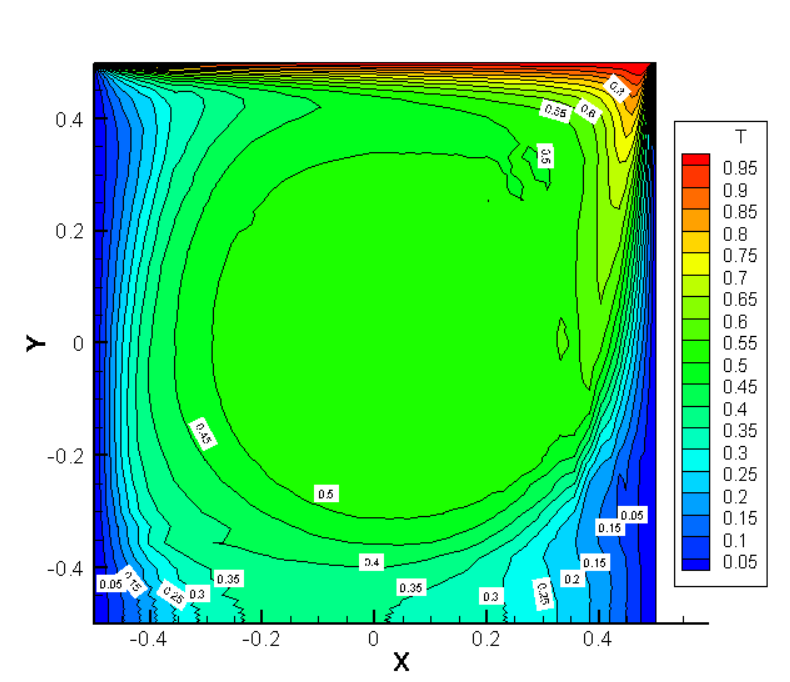
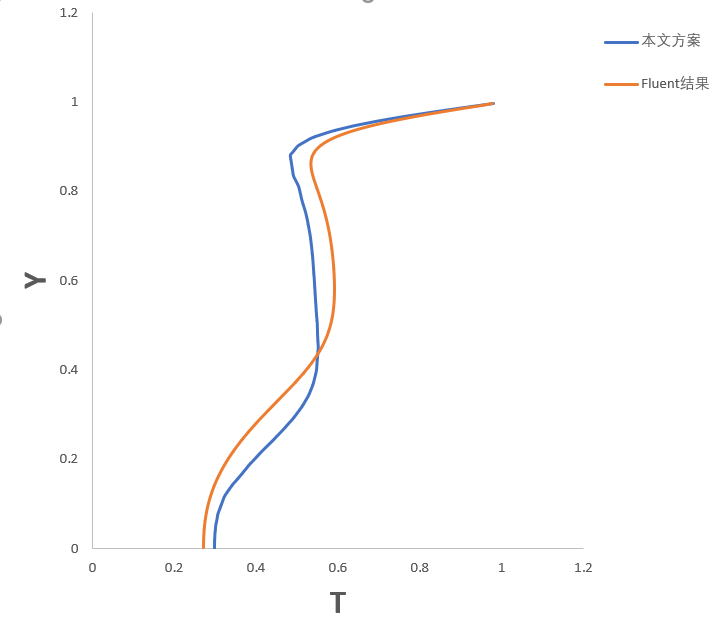
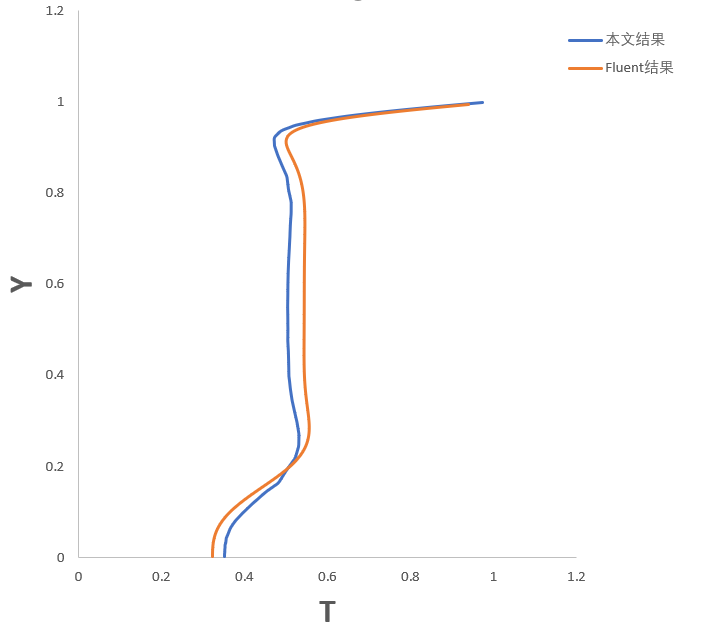
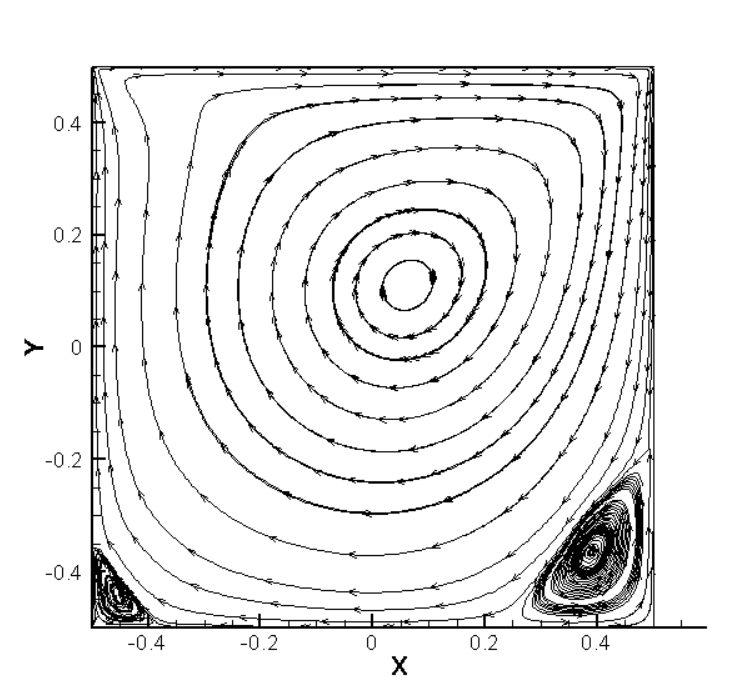
3.1 热方腔流（程序验证） 16

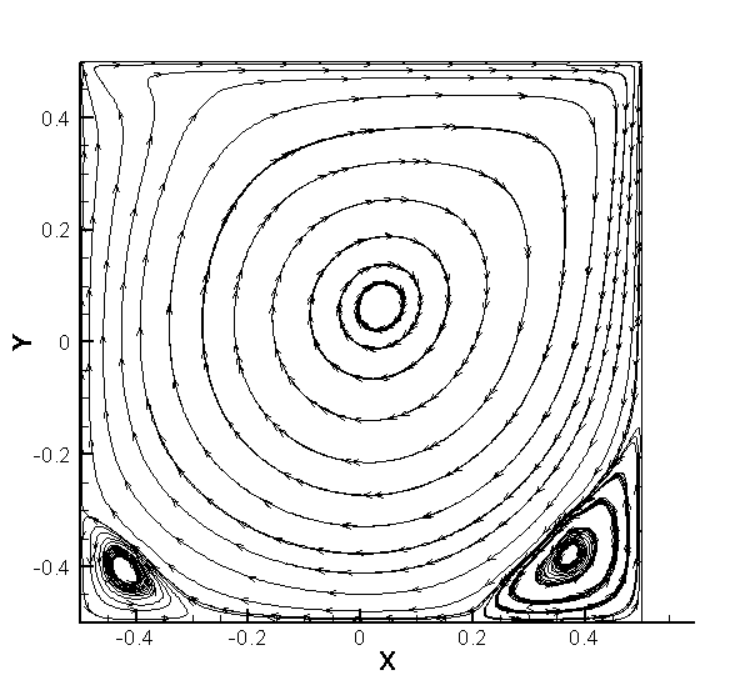
3.2 四边盖驱动问题（程序应用） 24

第4章 总结与展望 33

4.1 总结 33

4.2 展望 33

致 谢 34

参考文献 35

第一章 绪论

1.1 研究背景

流体是自然界中最常见的物质，例如水，空气等，也是工程机械中最为常见的工质。人类社会生产生活的发展，在许多方面迫切地需要对流体系统做出精确的描述。目前人们对流体系统的描述主要有三种模型：微观分子动力学模型、介观模型和宏观连续模型。微观分子动力学模型的基本出发点在于，通过对流体系统里的每个粒子运用牛顿力学，试图运用牛顿力学清晰地刻画每个分子的动力学行为，然后通过统计的方法导出宏观力学量。这种方法思路很简单，算法也很简单，但是由于真实流体包含大量的分子（的量级），使得这种方法计算量较大，一般仅限于微尺度下，短时间内的流动；宏观连续模型是将流体作为一个整体，建立合适的力学方程，然后通过初值条件与边界条件进行求解，例如Euler方程，Navier-stokes方程等^[7,8]，此类模型是流体应用和研究过程中经常采用的模型；另外，还有一种所谓的介观模型，其是基于粒子的分布函数，通过研究粒子的分布函数随时空的演化，并通过宏观物理量与分布函数的关系求得流体系统的宏观物理量的模型方法^[6]。事实上，基于Boltzmann-BGK方程，通过Chapman－Enskog展开分析，我们可以从高阶近似下恢复宏观控制方程。由此可见宏观控制方程不过是微观统计的一种近似。

近年来，基于格子玻尔兹曼-BGK方程^[1]的格子Boltzmann方法（LBM）在模拟等温不可压缩流动领域取得了巨大的成功^[2,3]，其方法简单、效率高、边界条件容易处理，已经被广泛应用。然而传统的LBM一般仅限于等温流动，尽管近年来，描述非等温流动的各种LBM也相继被提出，但是标准LBM仅能应用于均匀网格，对复杂边界缺乏良好的适应性^[6]。针对该问题，一种基于有限体积框架的格子Boltzmann方法（FVLBM）被提出，并受到了研究人员的关注^[16,17]。另外，应用LBM求解温度场控制方程时，由于离散速度的关系，通常需要求解的方程数量较原始传热方程数量多得多，大大增加了对计算的效率和内存的存储量的需求^[10,11,13]。而气体动理论格式（GKS）是另外一种基于玻尔兹曼方程的一种有限体积形式介观方法^[4,5,9]，它可以直接针对宏观控制方程求解，利用BGK方程的形式解，构造单元界面上的分布函数，巧妙地将BGK方程中的碰撞与对流两个过程结合在一起。整个格式的计算中，流场信息只需要通过宏观守恒量进行记录和更新，这使得GKS的求解和基于宏观守恒量的有限体积法的求解具有类似的过程，包括单元内守恒量重构、界面上气体演化求数值通量、通过界面通量计算单元内守恒量均值的投影量三个步骤^[5,12,14]。GKS求解流动控制方程的思路是通过有限体积法，求解单元界面的守恒量，因此可以很自然地应用于非均匀网格^[14,15]。

1.2 目的及意义

本论文研究的目的在于结合GKS和FVLBM的优缺点，针对不可压缩对流传热问题，发展一种有限体积格子Boltzmann方法和气体动理论BGK格式的混合数值方法。该方法能够处理带有复杂边界条件的非等温流动问题，本项研究可为数值模拟和研究在科学研究和工程实际中广泛存在的不可压缩对流传热问题，提供一种新的高效率、高精度工具，具有重要的科学意义和工程应用价值。

1.3 有限体积LBM与GKS简介

1.3.1 有限体积LBM

有限体积LBM模型（Finite-Volume LBM , FVLBM）最早由Nannelli和Succi等人提出^[18]。与标准格子Blotzmann 方法相比，它依然采用速度离散离散模型^[19]：

这里，Boltzmann方程碰撞项选用的BGK格式^[1]，为平衡分布函数，为粒子微观速度，为松弛时间

不同的是，标准格子Blotzmann 方法中的分布函数只能在离散的速度方向上“运动”；而有限体积LBM采用任意形状的非均匀网格，并对网格积分，在这里我们假设了由单元中心分布函数值代替整个单元积分运算，从而得到单元中心分布函数对时间t的关系式：

这里，为单元网格的面积或者体积；为（1）式左边第二项与右边第一项对网格区域积分得到的含时项

因为（2）式为一阶常微分方程，因此可通过数值解法得到在时刻与时刻的关系，从而不断更新的值。再根据分布函数与宏观守恒量的关系，我们便可以不断更新单元的宏观守恒量。

尽管近年来，基于不同的离散方法，各种不同FVLBM被相应提出，但在数值精度上问题上尚不成熟^[6]，还有待发展。此外，用FVLBM的方法模拟温度场时，因需求解的方程数量偏多，故本文只在模拟速度场的时使用FVLBM。

1.3.2 GKS概述

GKS（Gas Kinetic Scheme）是一种基于气体动理论（gas-kinetic theory）的数值模拟方法^[20,21,22]，采用的是有限体积格式；与传统有限体积方法不同的是，GKS的核心并不是对宏观控制方程进行离散，而是从Boltzmann-BGK方程出发构造的数值模拟方法。

有限体积方法^[5]计算公式一般可以写为：

在这里，Q为单元宏观守恒量，而为为宏观控制方程里的相关宏观量

从（3）式可知，我们只要能求得单元边界处的数值通量，即可更新单元的宏观守恒量；对于传统的有限体积方法，为求得单元边界处的数值通量，往往要从宏观控制方程出发在单元界面构造数值通量^[5,9,14]。然而，我们可以通过Chapman－Enskog展开分析^[6,8,11]得到宏观控制方程与Boltzmann－BGK方程的关系，进而得到单元边界数值通量与分布函数关系。

如此看来，我们就能把求单元边界数值通量的问题转化为求解单元边界处粒子分布函数的问题，而不用再去构造另外一种专门的算法求解数值通量。这种方法既能够模拟等温流动，也能够模拟非等温流动，因此本文采用这种方法来计算温度场。

1.4 本文研究内容及创新点

1.4.1 研究内容

1）基本内容

1. 针对温度场的对流传热方程，建立用以描述对流传热过程的气体动理论Boltzmann-BGK模型；
2. 基于上述气体动理论Boltzmann-BGK模型，利用Boltzmann-BGK模型方程的形式解，建立可用于温度场求解的气体动理论BGK格式（GKS）；
3. 研究流场求解的有限体积格子Boltzmann方法和温度场求解的气体动理论格式的耦合方法，建立有限体积格子Boltzmann方法和气体动理论BGK格式的混合数值方法。

2）算例测试与结果评估

A. 基于已建立的数值模型，用Fortran编写程序

B. 用Gambit进行网格划分，再用Tecplot 360 进行可视化

C. 基于上步得到的几个算例仿真结果，对仿真结果进行误差分析与评估

1.4.2 本文创新点

1）基于同一非结构性网格，提出了一种FVLBM与GKS耦合的数值算法，进行了速度和温度的计算，而非用单一的方法同时计算两者

2）能够很好地处理带有复杂边界问题的非等温流动。

第二章 非等温流动的FVLBM与GKS混合算法

2.1求解速度场的FVLBM算法

2.1.1 格子Boltzmann方程的数值离散

在本文中，为简便起见，我们以二维问题为例；选取模型，并且基于三角形网格，如下图：

图1 三角形网格示意图

Boltzmann方程用气体分布函数随时空演化来表示粒子系统动力学行为，表示为：

上式中，为粒子的微观速度； 为气体分布函数； 为碰撞项

因碰撞项及其复杂，而且还是一个非线性项，从原始方程进行数值求解非常困难，于是我们采用其BGK近似模型：

其中 是时间弛豫因子，与流体本身有关, 是气体平衡分布函数，

对BGK模型进行速度离散得到：

这里^[19]

其中，为流体宏观流动速度；为权系数；与声速有关，在中取为1/3。

根据宏观量与分布函数的关系，可得到下列式子：

这里， 表示流体的密度；

现在我们对（6）式左右两边同时积分，积分区域为第 个网格，得到：

利用高斯公式，（10）式可变为：

这里，对于（10）式左边第一项积分，我们使用了单元网格中心值来简化积分， 为第个网格的面积；此外，如图1所示，为单元边界的法向量，为边界长度，为边界中心分布函数值。

2.1.2 网格边界中心的分布函数重构

从（11）式可以看出，要求得 随时间的演化，方程中还有是未知项，现在的关键在于的取法，因为最后模拟结果的精度对其取法很敏感。

如果直接用两单元相邻边界左右两侧分布函数值的平均值代替其相邻边界中心分布函数值，则其精度不够，现已有相关研究员证明^[23]，通过以下的取法会有较好的精度：

j

i

R

L

图2 单元边界两侧分布函数

2.1.3 单元中心分布函数梯度计算

现在我们计算与，取一阶泰勒展开近似

上式中：为单元 与单元相邻边界中点坐标

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：