摘 要

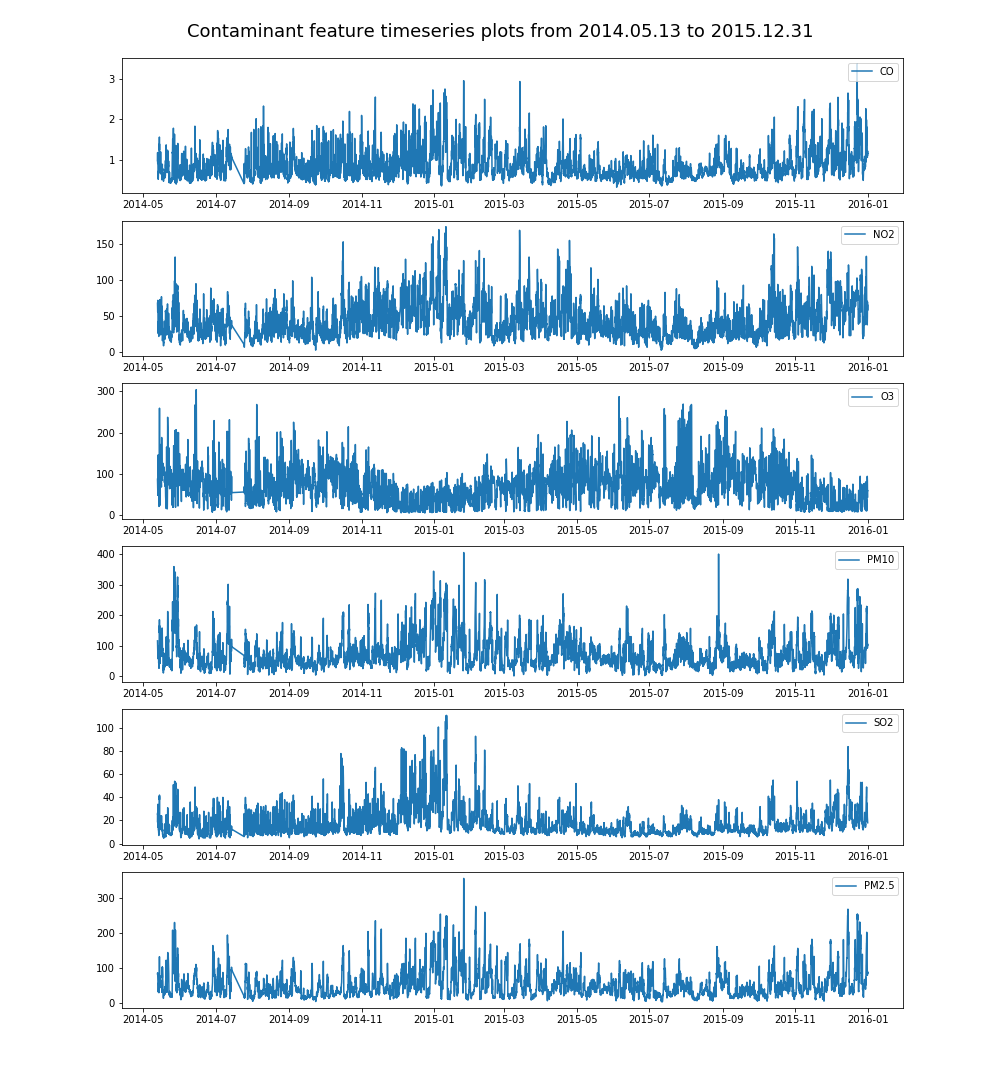
在环境污染问题备受关注的今天，如何有效地治理雾霾问题成为了大气环境科研者甚至是普通大众日益关心的问题，而霾的主要成分之一是PM2.5，所以治理雾霾问题的切入点之一便是降低日益严重的PM2.5浓度。本文基于上海市2014年5月至2015年12月期间的气象条件和空气污染物的数据，对数据进行了数据集成、特征清理、定性特征转换、特征标准化、特征选择等处理，对各特征和PM2.5浓度的相关性进行了分析。

运用线性回归、随机森林、长短时记忆神经网络，设计了三种不同时间窗口步长的PM2.5浓度预测算法，以适应不同的预测需求，结果表明，线性回归预测步长最短，随机森林较长，长短时记忆网络最长。

关键词：PM2.5浓度预测；线性回归；随机森林；长短时记忆网络

Abstract

Today, when environmental pollution is of great concern, how to effectively manage the haze problem has become an increasingly concerned issue for researchers at the atmospheric environment and even the general public. One of the main components of cockroaches is PM2.5, so the problem of smog One of the entry points is to reduce the increasing concentration of PM2.5. Based on the meteorological conditions and air pollutant data from May 2014 to December 2015 in Shanghai, this paper carries out data integration, feature cleaning, qualitative feature conversion, feature standardization, feature selection, etc. on the data. The correlation of PM2.5 concentrations was analyzed.

Using linear regression, random forest, long and short time memory neural network, three different time window step size PM2.5 concentration prediction algorithms were designed to adapt to different prediction requirements. The results show that linear regression prediction has the shortest step size and random forest. Long, long and short memory networks are the longest.

Key Words: PM2.5 concentration prediction; linear regression; random forest; long and short time memory network

目录

第1章 绪论 1

1.1 选题背景 1

1.2 国内外研究现状 1

1.3 研究内容 2

第2章 PM2.5回归预测算法概述 4

2.1 线性回归预测方法 4

2.1.1 算法原理 4

2.1.2 算法优化 4

2.1.3 线性回归正则化 5

2.2 随机森林预测算法 5

2.2.1 算法原理 5

2.3 神经网络回归预测算法 6

2.3.1 循环神经网络（RNN） 6

2.3.2 长短时记忆网络（LSTM） 7

2.4 算法优化 9

2.4.1梯度下降法 9

2.4.2动量梯度下降 10

第3章 数据获取及预处理 11

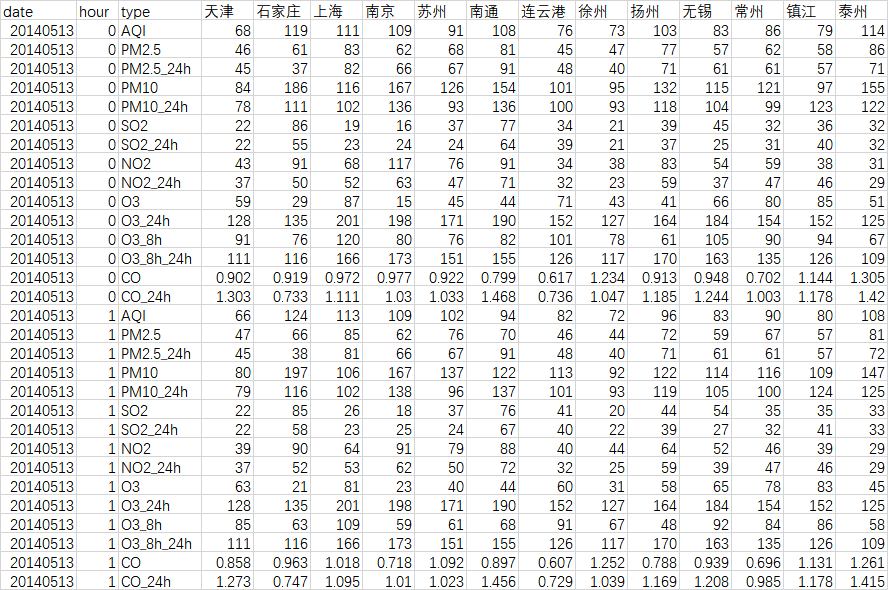
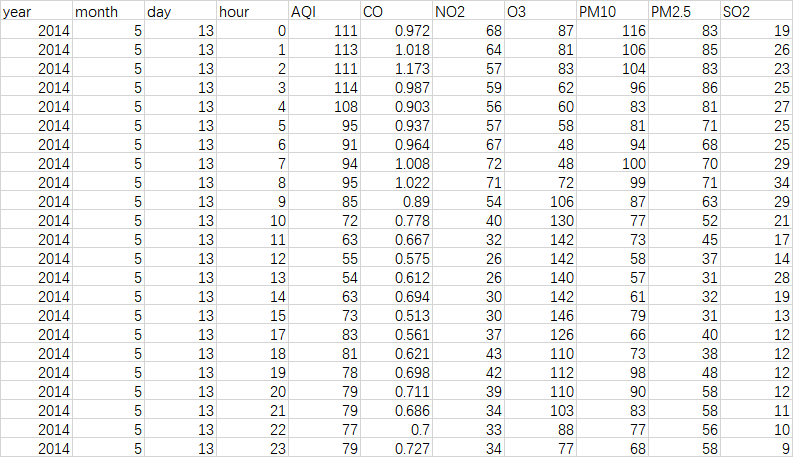
3.1 数据获取 11

3.2 数据集成 12

3.3 特征处理 13

3.3.1 特征清理 13

3.3.1.1去除无用特征 13

3.3.1.2缺失值处理 14

3.3.2 特征变换 15

3.3.2.1定性特征处理 15

3.3.2.2特征缩放 15

3.3.3 特征选择 16

第4章 PM2.5浓度预测 17

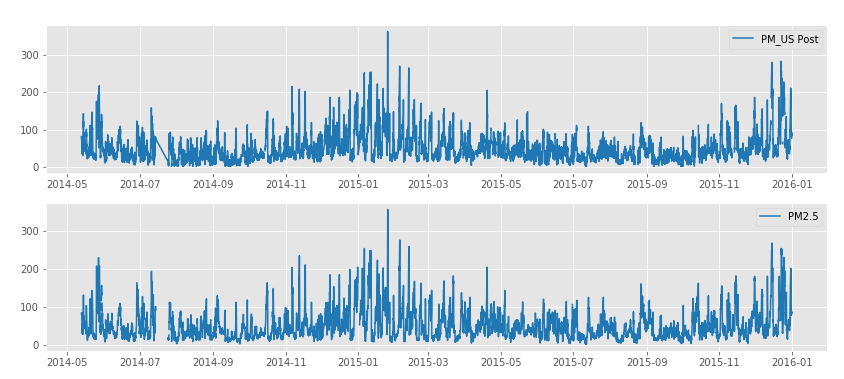
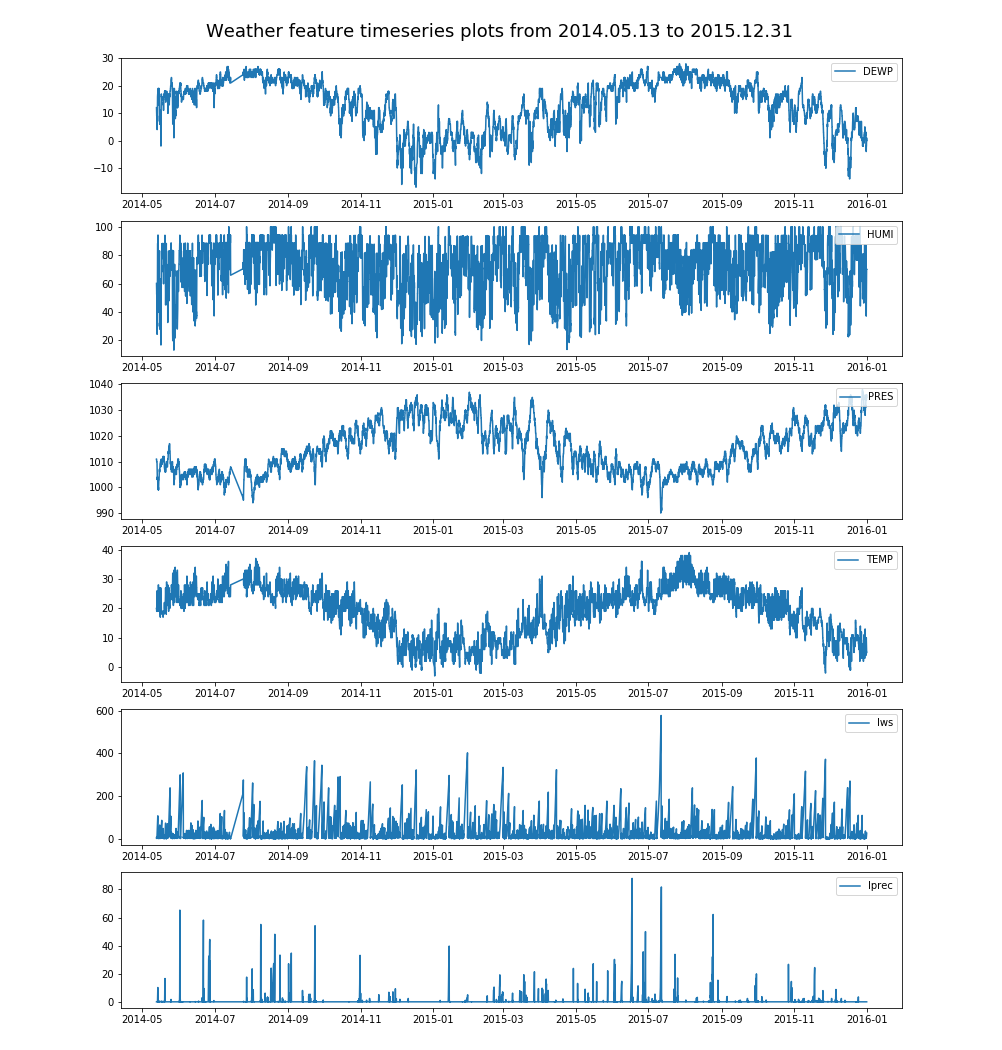
4.1 探索性分析 17

4.1.1 特征分布探索 17

4.1.2 相关性分析 18

4.1.2.1相关系数 18

4.1.2.2相关性可视化 20

4.2 模型评价指标 23

4.2.1 误差评价指标 23

4.2.2 可解释性评价指标 24

4.3 线性回归预测 24

4.3.1 单时间窗口预测 24

4.3.2 多时间窗口预测 26

4.4 随机森林预测 28

4.4.1 单时间窗口预测 28

4.4.2 多时间窗口预测 30

4.5 LSTM预测 32

4.5.1 单时间窗口预测 33

4.5.2 多时间窗口预测 35

第5章 总结和展望 37

5.1总结 37

5.2展望 37

参考文献 38

致谢 39

第1章 绪论

1.1 选题背景

近年来，国内快速的工业化导致空气污染大量增加，日益严重的空气污染导致中风、心脏病、肺癌等疾病患病率的增加。雾霾污染已经引起了广泛的关注，对人们的生活产生了很大的影响。

PM2.5是指直径为2.5微米或更小的颗粒物，已达到可进入人体肺泡的水平。PM2.5及直径更小的颗粒物，会通过人体鼻腔、咽喉下行，最终进入全身血液循环，对人体的呼吸和心血管系统形成不可逆的损害。PM2.5是霾的主要成分，也是霾天气的“最大元凶”，所以治理雾霾问题的切入点之一便是降低日益严重的PM2.5浓度，而如能对其浓度及时预测并采取行动便能在一定程度上缓解这种问题。

信息技术高速发展的结果之一是每日会生成数以万计的数据，如此大规模数据的背后是可挖掘的商业价值。数据非常庞大，计算所需的时间也在增加，幸运的是如今的硬件设备可以满足快速计算的需求，可以帮助人们在最短的时间内获得大量数据并对其进行分析运算。PM2.5浓度的预测问题涉及到较大规模的数据，包括气象、空气污染物、交通路况、生产活动、节假日、环境政策法规等在内的因素都对PM2.5产生一定的影响。

不同于传统的数据挖掘，使用如今备受关注的机器学习，可以使计算机能够从数据中学习，甚至可以自我改进。机器学习的基本前提是构建可以接收输入数据的算法，并使用统计分析来预测输出，同时在新数据可用时更新输出。

1.2 国内外研究现状

因美国的“洛杉矶光化学烟雾”事件和英国的“伦敦烟雾”事件，以及国内的雾霾问题是近年来才日益被重视起来的，所以国外对雾霾的研究早于国内很多年。

针对PM2.5的组成和成因，Minguill等人用正定矩阵分析了瑞士PM2.5的主要组成和形成因素^[1]。Georage D 等人利用回归模型研究了雅典气象特征与粒子浓度的关系，得出PM2.5与CO和氮氧化物高度相关，与风速呈负相关的结论^[2]。国内学者也对雾霾的特征和成因进行了研究。王继志等人研究了低能见度霾天气，并介绍了几种适用于这种天气条件下雾霾的诊断分析和预测方法^[3]。

针对PM2.5浓度的预测，国内外学者也进行了很多研究：基于随机森林回归算法，蔡永川等选取 30个特征因素，提出了PM2.5浓度快速预测模型^[4]。任才溶以时间、气象、站点关联性等特征，基于随机森林构建了对太原市PM2.5进行预测的模型^[5]。王云中利用线性回归、BP神经网络、长短时记忆网络对西安的PM2.5浓度进行了预测，提出了针对不同预测步长的不同预测模型，得出LSTM在预测1-15小时的误差较小，BP神经网络在预测16-72小时误差较小。周永生设计了基于LSTM的可处理含缺失数据的PM2.5预测模型，并和SVR、随机森林进行了对比，表明了LSTM预测率最高^[6]。

1.3 研究内容

基于2014年5月13日至2015年12月31日的空气污染物和气象历史数据，本文使用机器学习方法有效预测了上海市未来的PM2.5小时浓度，准确的预测可以及时地告知公众和相关部门并使其采取适当措施，保护大家的健康。本文的主要结构和内容如下：

第1章论述了选题背景及选题意义，并进行了大量的文献综述，了解了国内外学者对相关领域问题的研究现状，随后介绍了文章的研究内容和行文结构。

第2章对本文预测PM2.5浓度用到的回归算法进行了原理概述，分别为线性回归、随机森林、长短时记忆网络。

第3章对本文研究所需的数据获取及预处理方法进行了说明，主要包括数据获取、数据集成、特征处理三个步骤。

第4章利用历史污染物数据和未来的气象数据，探寻未来的 PM2.5 浓度和历史浓度以及最近的气象数据的关联性，并运用三种回归算法对未来时刻的PM2.5浓度进行预测，不同的预测时长可以满足对未来PM2.5浓度变化更精细的预测需求。

本文的技术路线如图1.1所示。

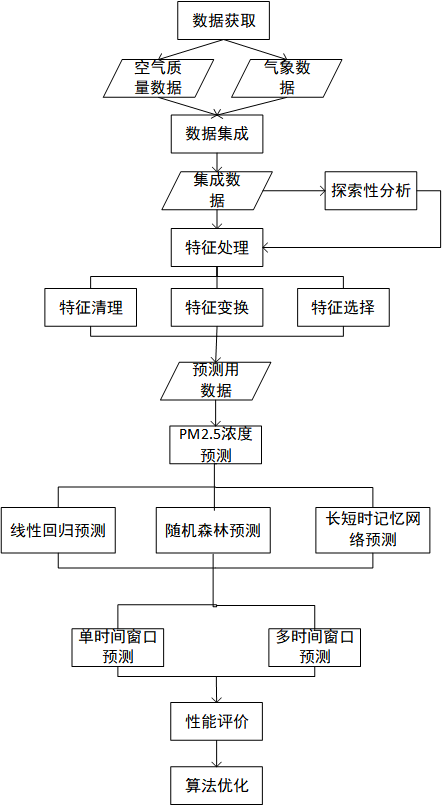
图1.1 技术路线

第2章 PM2.5回归预测算法概述

2.1 线性回归预测方法

大量研究表明PM2.5浓度和大部分气象、空气污染物之间存在明显的线性相关关系，因此可首先考虑使用最简单、基础的线性回归算法进行预测。

2.1.1 算法原理

线性回归算法通过自变量之间的线性组合进行预测，目的是找到一条直线或者一个超平面，使预测值与真实值之间的误差最小化。多元线性回归模型表达式见公式2.1。

其中，为权值系数，为样本的特征值，为方便表达和计算，引入一个特征，公式2.1等价于公式2.2

进一步，如下式子用矩阵可更加简介地表示公式为2.3，其中为维矩阵，为维向量，m为样本数，n 1为特征数。

通过不断地优化损失函数可求解，最常用损失函数的定义为残差平方和，见公式2.4

公式2.4更为简洁的矩阵表达式为公式2.5

2.1.2 算法优化

对公式2.4的优化有两种办法，一是梯度下降法，二是最小二乘法。

梯度下降法通过选取适当的初值，不断迭代，更新x值，最小化目标函数，直到收敛。由于负梯度方向是使函数值下降最快的方向，所以x的值在迭代的每一步都在负梯度方向上更新，从而减小函数值。对于公式， 的更新公式见公式2.6，通过不断执行此式直至收敛。

最小二乘法利用了在极值处导数为0的性质，直接建立等式方程进行代数求解，在公式22中，令对的导数为0，即可得的解，见公式2.7

最小二乘法虽简洁易懂，但也有应用的局限性，首先该方法要求矩阵是可逆的，对于不可逆的情况是不适用的；其次，当特征数n很大时，矩阵的求逆运算很费时，因此不适用于特征数很大的情况；最后，最小二乘法只适用于假设函数是线性的情况。这几点问题在梯度下降法中都是不存在的，因此后者的适用性更广，成为了机器学习中常见的优化算法。

2.1.3 线性回归正则化

正则项是添加到损失函数中的一个项，用于防止模型过度拟合，常见的有L1和L2正则。L1正则项在参数 的L1范数上乘以一个系数，可以控制正则项和残差平方和的权重大小，L1正则项通过使一些特征的系数变为0或者接近0，起到了过滤相对不重要特征的作用，从而避免过拟合，增强了模型的泛化能力。在线性回归中，L1正则通常称为Lasso回归，公式2.5加入L1正则项后为公式2.8，可通过坐标轴下降法或最小角回归法求解。

同理，L2正则项在参数的L2范数的平方上乘以一个系数，L2正则项不会过滤任一特征，而是缩小其特征系数。L2正则被称为Ridge回归或者岭回归，公式2.5加入L2正则项后为公式2.9，可使用最小二乘法对Ridge回归进行求解。

2.2 随机森林预测算法

2.2.1 算法原理

随机森林是一种集成学习方法，其由很多同质的CART决策树组成，决策树之间彼此不存在相互依赖，而是并行的，可并行也是随机森林的一个优点，数据规模很大时会有速度上的优势。集成学习中将这样的单棵决策树称之为弱学习器，而很多弱学习器通过某种集成策略可以集成为强学习器，展现出更好的效果，模型性能会随着决策树数量的增加而变好，然而过多也会导致计算量的增大，训练时间增长。

每一棵决策树采取一种称为自助采样法的采样方法，这是一种放回抽样，抽样次数和原样本数相同，随机性的缘故导致每一棵决策树的样本都是不同的，当样本数足够大时，每次采样大约有36.8%的数据不会被采集到，增强了模型的泛化能力。另外，在特征选择上也和普通的决策树不同，普通的决策树会在节点上选择所有样本中的最优特征进行子节点划分，而随机森林中的决策树会采取节点中一部分样本的最优特征，如此也可增强模型的泛化能力。

针对回归预测问题的集成策略一般采用平均法，即将所有弱学习器的输出平均作为最终的模型输出。平均的方法有简单的算数平均，也可对每一学习器赋予权重再平均。

2.3 神经网络回归预测算法

大量研究表明，PM2.5的浓度值不仅和当前时刻的气象、污染物特征相关，也和最近一段时间内的这些特征相关，是一种典型的时间序列预测问题，这便要求预测模型能够将不同时间上的信息相互联系起来，预测当前时刻能考虑到过去的特征，并依次向前推进。

2.3.1 循环神经网络（RNN）

在神经网络中，不同于传统的神经网络，循环神经网络（Recurrent Neural Network，RNN）具备“记忆”历史信息的特性，图3.1是RNN按照时间线的展开图，图中t为2时的不仅和输入值有关，还和上一时刻隐藏层状态值有关，它们的关系如公式2.10，而每个时刻的输出值y的计算公式如2.11

将公式2.10代入公式2.11，可得

由上面的连等式可以看到是和、、…有关的，这便证明了确实能够RNN“记忆”历史信息。

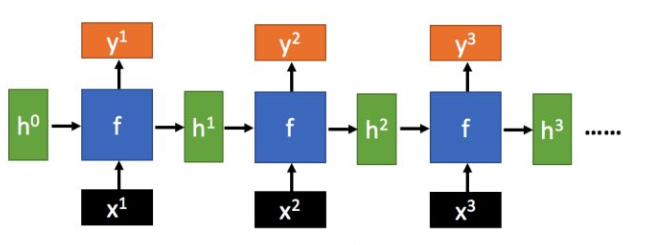
图3.1 RNN时间线展开图

RNN在自然语言处理领域可用于机器翻译、语音识别等，在计算机视觉领域可用于生成图像描述，已经获得了广泛应用。然而，在传统的RNN中，在梯度反向传播阶段，梯度最终可能通过与神经元之间的连接相关联的权重矩阵倍增，这意味着转换矩阵中的权重会对学习过程产生很大影响。

当权重矩阵的特征值小于1，可能造成消失梯度的情况，梯度变得很小，以至于学习变得非常慢或完全停止工作，学习带有数据长期依赖性的任务也会变得更加困难。相反，当权重矩阵的特征值大于1，可能会导致梯度太大并影响收敛，这通常被称为梯度爆炸。其中，梯度爆炸可以通过剪裁来解决，而梯度消失问题却不好解决。因为存在这样的问题，尽管RNN在理论上能够“记忆”任意长时间的历史信息，但实际应用中却不如人意。

2.3.2 长短时记忆网络（LSTM）

长短时记忆（Long Short-Term Memory，LSTM）网络由Hochreiter和Schmidhuber ^[1]提出，由于其在精确建模数据中的短期和长期依赖性方面的卓越性能而被广泛使用。

LSTM已经被用于许多序列学习应用，特别是在自然语言处理领域。Graves和Schmidhuber^[7]利用LSTM在Graves等人的未分段连接手写识别中取得了显著的结果。在自动语音识别中，eck和schmidhuber^[8]将其应用在音乐创作中，gers和schmidhuber^[9]将其应用在语法学习中。在图像标记方面也取得了进一步的成功，利用LSTM与卷积神经网络配对可以自动提供图像注释^[10]。

然而，很少有工作将LSTM应用于实值时间序列的预测。 Ma等人^[11]评估了几种RNN在短期交通速度预测中的表现，并将其与其他常用方法（如SVM，ARIMA和卡尔曼滤波器）进行了比较，发现LSTM网络几乎总是最好的方法。 Pawlowski和Kurach ^[12]结合LSTM和前馈神经网络，通过预测未来的甲烷浓度值来对煤矿中的危险等级进行评级。通过采用混合方法，Felder等人^[13]训练LSTM网络输出最适合风力时间分布的高斯混合模型的参数。

LSTM解决了RNN梯度消失的问题，其工作方式与RNN架构基本相同，不同之处在于它实现了一个称为记忆细胞更精细的内部处理单元。记忆细胞是线性自连接的，权重接近1，在没有外部干扰的情况下，细胞状态可以从一个时间步长到另一个时间步长保持不变。记忆细胞由三个主要部分组成：输入门、遗忘门和输出门。门用于调节细胞本身与其环境之间的相互作用。遗忘门可以调节细胞的自回归连接，允许细胞根据需要记住或忘记其先前的状态，输入门通过是否允许输入改变细胞的状态，而输出门通过输出细胞的状态来影响其他神经元。

自LSTM最初的定义^[14]以来，文献中已经提出了原始LSTM单元的几种变体。本文参考Graves和Schmidhuber ^[15]提出的常用架构。 图3.2展示了LSTM的内部结构以及两层细胞之间的信息传递，公式2.13至2.18描述了如何在每个时间步更新一层细胞。

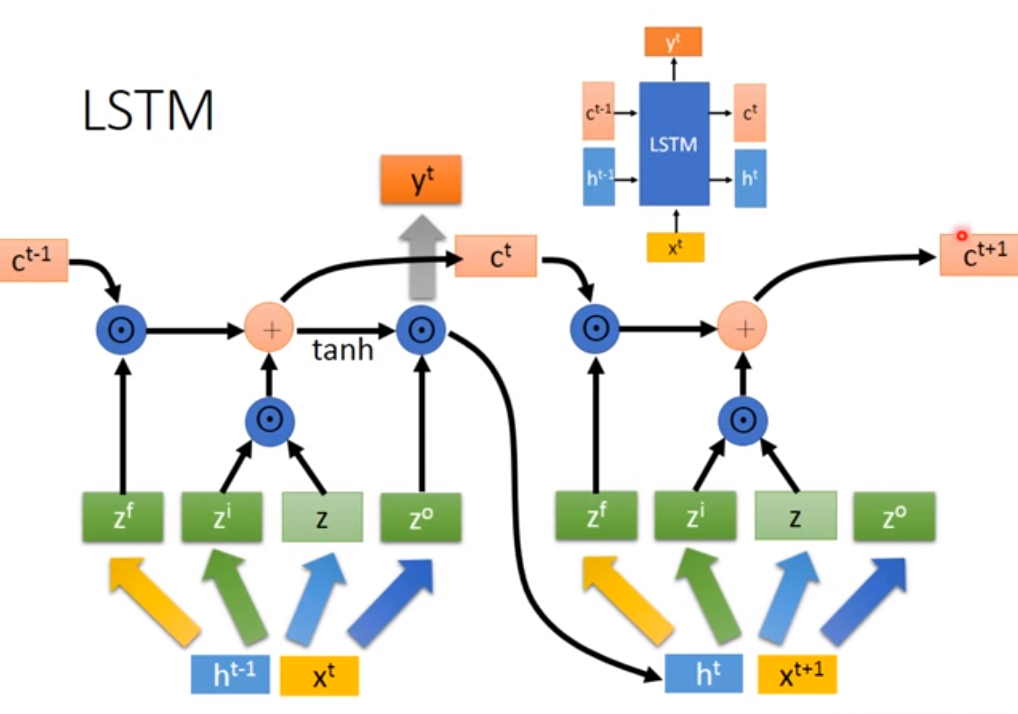
图3.2 LSTM结构及信息传递示意图

首先，计算时间 t 时细胞遗忘门的激活值：

作为遗忘门控，用来控制上一状态的中哪些信息可以传入当前时间t，即控制哪些信息被保留，哪些被遗忘。表示sigmoid二值函数，输出0到1之间的值，0表示信息被遗忘，1表示被保留，输入门和输出门控制原理同遗忘门。此为第一阶段，筛选上一时间的信息。

其次，计算输入门，以及 t 时细胞状态的候选值：

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：