基于SVM的复合ZIP参数辨识与电子负载建模外文翻译资料
2021-12-16 23:12:37
基于SVM的复合ZIP参数辨识与电子负载建模
Chong Wang , Member, IEEE, Zhaoyu Wang , Member, IEEE, Jianhui Wang , Senior Member, IEEE, and Dongbo Zhao, Senior Member, IEEE
摘要:利用支持向量机(SVM)方法,提出了一种复合ZIP和电子负载的参数识别技术。由于电子负载的有功功率和无功功率是电压幅度的分段函数,电子负载的工作模式由电压幅度决定。为了提高参数识别的准确性,采用了两个滤波器 (Hampel和Savitzky–Golay) 进行预处理测量,以降低噪声。降噪后的数据作为用支持向量机方法求解的回归模型的训练数据。数值结果表明,采用滤波器的支持向量机方法能够高精度地识别复合ZIP和电子负载模型的参数。
关键词:电子负载、降噪、参数识别、支持向量机、ZIP负载
一 简介
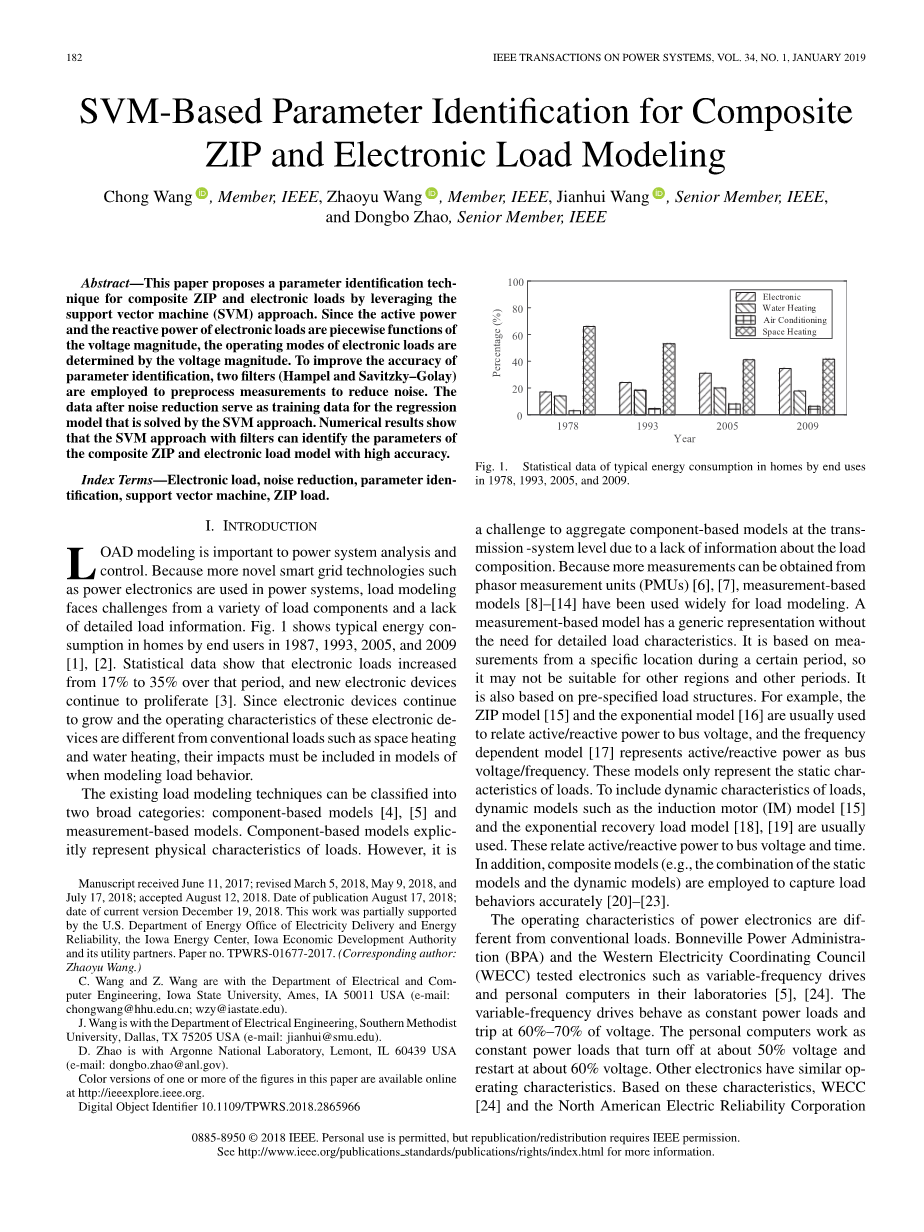
负载建模对电力系统的分析和控制具有重要意义。由于电力系统中使用了更多新颖的智能电网技术 (如电力电子技术), 负载建模面临着各种负载组件和缺乏详细负载信息的挑战。图1显示了1987年、1993年、2005年和2009年最终用户在家中的典型能耗 [1],[2]。统计数据显示, 电子负载在这一期间从17% 增加到 35%, 并且新的电子设备继续激增[3]。由于电子设备继续增长,这些电子设备的工作特性不同于传统的负载,如空间加热和水加热,因此在模拟负载行为时,必须将其影响纳入模型。
图1. 1978年、1993年、2005年和2009年家庭终端使用的典型能源消耗统计数据。
现有的负载建模技术可分为两大类:基于组件的模型[4]、[5]和基于测量的模型。基于组件的模型明确表示负载的物理特性。但是,由于缺乏有关负载组成的信息,在传输系统中聚合基于组件的模型是一个挑战。由于可以从相量测量单元(PMUs)[6]、[7]中获得更多的测量值, 因此基于测量的模型[8]-[14]已被广泛用于负载建模。基于测量的模型具有通用表示形式,而不需要详细的负载特性。它基于特定时间段内特定位置的测量值,因此可能不适合其他区域和其他期间。它还基于预先指定的负载结构。例如,ZIP模型[15]和指数模型[16]通常用于将有功功率/无功功率与总线电压联系起来, 频率相关模型[17]将有功功率/无功功率表示为总线电压/频率。这些模型只表示负载的静态特性。为了包括负载的动态特性, 通常使用动态模型,如异步电动机(IM)模型[15]和指数恢复负载模型[18], [19]。这些都与有功/无功功率与总线电压和时间有关。此外, 还使用复合模型(例如, 静态模型和动态模型的组合)来准确捕获负载行为 [20]-[23]。
电力电子的工作特性不同于传统负载。邦尼维尔电力管理局(BPA) 和西部电力协调理事会(WECC)测试的电子设备, 如变频驱动和在他们的实验室的个人电脑[5],[24]变频驱动器的工作原理是恒定的功率负载,并以 60%-70% 的电压跳闸。个人电脑的工作原理是恒功率负载, 在50%左右的电压下关闭,并在60% 左右的电压下重新启动。其他电子产品具有相似的操作特性。基于这些特征, WECC [24]和北美电力可靠性公司 (NERC)[25]代表电子模型的分段相当于母线电压的功能。这些分段特征没有包括在现有的研究[15]-[23]。
图2 所提出的方法的框架
适当的载荷模型的参数通常通过非线性最小二乘法(NLS)进行优化, 以实现模型输出与记录测量之间的最小差。基于统计技术 [26]-[28] 和启发式技术 [29]-[31]的算法可用于识别参数,具有噪声的测量通常直接用作算法输入。但是, 测量[32]中的潜在异常值可能会偏离参数标识。此外,目前的算法不能处理表示为分段函数的电子模型的参数识别。
针对上述挑战, 提出了一种基于SVM的复合ZIP和电子负载模型参数辨识方法。本文的主要贡献有三: (1)电子负载的工作特性表现为电压方面的分段函数, 并提出了复合ZIP和电子负载模型。(2) 采用基于汉普尔滤波器和 Savitzky-Golay滤波器的降噪技术来降低噪声, 提高参数识别的精度。(3) 采用带有噪声滤波器的支持向量机算法对复合负载模型的参数进行识别。
本文的其余部分的结构如下。第二部分介绍了提出的ZIP参数识别框架和电子负载模型;第三部分介绍了复合ZIP和电子负载建模;第四部分介绍了参数识别算法;第五节给出了仿真结果;第六节总结了本文的结论。
二 构建参数识别的框架
图2显示了该方法的框架。该框架有三个关键步骤: 模式识别、降噪和参数识别。
1.模式识别: 由于电子负载的功耗可以表示为电压大小的分段函数, 因此不同的电压大小可能会导致不同的工作模式。在这一步中, 首先进行电压跳转检查, 然后根据电压测量进行曲线拟合, 根据电压幅度获得工作模式。利用操作模式, 可以确定复合ZIP和电子负载的回归模型。详细信息将在以下各节中进行说明。
2.降噪: 在实际电压测量和功率测量的基础上, 将降噪后的一组新数据作为训练数据,以提高参数识别的准确性。通过汉普尔滤波器和 Savitzky-Golay 滤波器从实际测量中减少噪声, 获得了清理后的数据。
3.参数识别: 基于降噪后的新数据组,采用支持向量机方法对复合ZIP和电子负载的回归模型参数进行识别。
三 复合ZIP与电子负荷建模
本部分首先给出了ZIP和电子负载模型的数学公式, 然后给出了复合ZIP和电子负载模型回归模型的推导。
1.ZIP模型
ZIP模型是典型的静态负载模型之一。它包括恒阻抗(Z)、恒流(I)和恒功率 (P)。它通常被用来表示功率和电压之间的关系。数学公式表示如下:
(1)
(2)
其中和分别为有功功率和无功功率, 在时间t所关注的总线上, 为额定电压,和分别为基本的主动/无功功率。 是时间 t 时的电压幅度。 、和 是ZIP负载的有功功率参数, 它们满足 =1。、和是ZIP负载的无功功率参数,它们满足 =1。(1) 左侧的第一个术语表示恒定阻抗负载的有功功率, 而是恒定电导。(1) 左侧的第二个术语表示恒流负载的有功功率, 而是恒流。第三个术语代表恒定的功率装载的有功功率, 并且 是恒定的功率。
表一电子负荷系数
2. 电子模型
在软件power world 中定义的电子负载具有以下特征:
如果端电压高于阈值, 则电子负载的有功功率和无功功率为P 和Q 常数。
如果电压介于两个阈值 和 ( gt; ) 之间, 则电子负载的有功功率和无功功率线性降低到零。
代表电子负载的一小部分。如果大于零, 则随着电压的恢复, 它将线性地重新连接。
WECC复合负载模型中定义的电子负载与 power world 中定义的电子负载相似,其数学公式表示如下:
(3a)
(3b)
其中 和 分别是电子负载在时间t的有功/无功功率。和分别是基本的有功/无功功率。是一个与总线电压相关的系数, 在表 1 中列出。模式取决于终端电压。
在表 1中, 和是两个阈值,是从低压跳闸中恢复的电子负载的一小部分。是跟踪最低电压但不低于的值, 它是每个样本的已知值。它的价值可以表示如下:
(4)
如表1所示, 电子负载的模式取决于其端电压。为了说明不同条件下的电子负载模式, 我们在图3中给出了一个例子。我们假设我们有一个电压曲线, 它不仅受到负载的影响, 而且也受到外部电网的影响,如图 3(a) 所示。因为被定义为跟踪最低电压, 它的轨迹从到是与在图 3(a)轨迹相同的, 因为 在这一期间逐渐减少, 如图 3(b)所示。从 到 , 保留值是 , 因为它不应该小于 。从到 , 保持值, 因为 小于 。
图3 (a) 电子负载的总线电压示例。(b) 每个样品的 的轨迹。(这五种模式是为了展示而使用的, 实际操作可能并不涵盖所有五种模式。)
根据表1中的条件, 根据WECC定义, 根据电压确定工作模式。以图3中的场景为例。从到 , 因为 ge; 和 ge;, 电子负载处于模式4。从 到, 电子模型处于模式 2, 因为 le;le; 和 le;。从 到 , 电子负载处于模式 1, 因为总线电压小于。从 到 和 到 , 电子负载分别处于模式3和模式5。在本研究中, 我们采用了由WECC定义的电子负载模型。
对于组件级负载, 电压阈值是已知的参数。对于包含许多电子负载的总负载, 我们可以首先将电子负载分为不同的类别;特定类别中的负载具有相同的电压阈值。然后, 我们使用表一中的标准来确定每个类别的载荷模式, 并得到不同模式下的复合模型参数的公式。由于不同类别具有不同的阈值, 因此聚合负载的模式是每个类别模式的笛卡尔乘积。
3. 建模
利用ZIP模型和电子负载模型, 可以将复合模型表示为:
(5a)
(5b)
其中和分别是代表整个有功/无功功率中电子负载部分的系数。和 分别是复合负载的有功、无功功率。
根据(1)和(2),我们知道ZIP负载的有功功率和无功功率是和 的函数。此外, 电子负载的有功功率和无功功率是根据(3a)、(3b)和(4)的函数。我们重写(5a)和(5a)作为
(6a)
(6b)
表二 复合材料模型的工作功率参数
其中表二列出了有源功率系数、和, 并在表二中列出了这些参数在五种模式下的详细公式。这五种模式的条件与表1中列出的条件相同。、和是无功功率系数, 它们与有功系数有相似的表达式。
四 参数识别的算法
本部分介绍电压跳转校验、模式识别曲线拟合、降噪噪声滤波器以及参数识别支持向量机。
1. 电压跳转校验
因为我们考虑稳态模型, 所以忽略了组件的高阶动力学。但是,由于不同的系统条件,电压可能会发生很大的变化。这个大的变化被认为是电压跃升。如果我们在跳转前后平滑所有样本的噪声, 噪声平滑后的数据可能与原始样本有很大的不同。为了解决这个问题, 我们分析了电压数据和电源数据,以检查是否发生电压跳转。当电压跃升发生时,相应的样品将不会一起使用以平滑噪声。当和时,电压发生跳转。和分别是在t和t-1的电压测量。和 分别是t和t-1的实际功率测量值。和是给定的阈值。由于噪声通常满足正态分布, 因此约99.7% 的噪声基于3西格玛规则在三个标准偏差范围内。由于电压跳转的值远远大于噪声, 因此可以将和设置为大于三个标准偏差 (例如, 六个标准偏差)。
2.曲线拟合
图4 曲线拟合的一个简单案例。
由于测量噪声, 当测量接近阈值和 时, 很难确定工作模式。例如, 图4中的示例 A、B、C、D、E和F位于阈值附近。如果我们直接使用样本A、B、C、D、E和F的值来确定模式, 则根据表 1中列出的模式条件, 操作在两种模式之间来回移动。噪声可能会影响模式选择。在实践中,我们应该使用真正的值来识别模式。因此,我们首先将阈值和周围的电压曲线拟合, 以帮助识别模式。在曲线拟合后, 样本A、B、C和D 被认为属于一种模式, 样本E和F被认为属于另一种模式。
我们使用具有第n度的多项式函数来适应曲线:
(7)
其中t是采样时间, 是系数。要找到系数, 我们可以解决以下问题:
其中是样品t的测量值。对于此优化, 我们可以围绕阈值和选择50个样本, 并选择具有三度或四度的多项式函数, 在这种情况下, 不会发生过度拟合。(8)中的模型是一个典型的最小二乘优化模型, 通过 Matlab 中的曲线拟合工具箱求解。
3.噪声过滤器
实际测量中的噪声对参数识别有很大的影响。负载建模的参数辨识在测量的基础上估计了负荷模型的未知参数。噪声和异常值会影响估计参数的准确性。为了保证参数识别的高精度,在实际测量的基础上,利用滤波器导出了一组新的数据。由于 Savitzky-Golay滤波器在更好地保持某些高频元件的振幅方面具有优势, 而Hampel滤波器在鲁棒异常值检测方面具有优势, 因此使用这两个滤波器来降低噪声。
图5 hampel过滤器
1) Hampel过滤器: Hampel过滤器通过Hampel标识符检测和删除噪音和异常值, 它取决于统计的三西格玛规则。例如, 图5中的具有包含自身的窗口的中值, 并且计算了两侧的l相邻样本:
(9)
其中是中值, 而l是滑动窗口的长度, 如图5所示。
此外, 每个样本相对于其窗口中值的标准偏差是通过使用中值绝对偏差计算的:
(10)
(11)
其中是标准偏差,.
如果样品满足情况, 其中N是一个给定的阈值, 样本 将被所取代。
图6 Savitzky-Golay过滤器
2) Savitzky-Golay过滤器: savitzky-golay过滤器依赖于最小二乘多项式拟合, 通过移动窗口与数据在时域中,如图6所示。对于示例, 我们考虑具有第n度的多项式:
(12)
其中 、,...,

英语原文共 12 页
资料编号:[4803]




