配有HF片的主缆和索鞍之间抗滑能力的理论和实验研究

王 路，沈锐利，王昌将，王 渊

摘要

对于多跨悬索桥，主缆与中间鞍座之间的滑移是一个关键问题。因此，必须找到有效的抗滑方案并提出相应的评估方法。在本研究中，提出了运用水平摩擦（HF）板的抗滑概念，并加以考虑了逐层滑移行为，然后建立了分析模型。并进行大规模模型试验以揭示HF板的影响并验证所提出的分析模型。而中国的瓯江北口大桥，就是一个典型的多跨悬索桥，可作为使用所提出的方法进行参数分析的实际案例，试验结果验证了所提出的分析模型能够对主缆的滑移行为作出可靠的预测。并且HF板可以显著提高主缆的抗滑能力，HF板在较低位置也将产生更大的抗滑效果和降低股线张力不均匀率。因此，所提出的方法有望广泛应用于多跨悬架桥的抗滑设计。

关键词：悬索桥; 滑动行为; 摩擦系数; 分析模型; 模型试验。

1 涉及水平摩擦片的介绍以及抗滑概念

多跨悬索桥具有显着的跨越能力并避免使用昂贵的共用锚地，已被公认为是跨越广阔水域的优秀解决方案(Yoshida et al.2004; Thai and Choi 2013; Zhang et al. 2016).多跨悬索桥的使用已被多次提出，例如美国旧金山-奥克兰海湾大桥，智利查考海峡大桥和中国青岛海湾大桥的概念设计。然而，由于主缆和中间鞍座之间尚未解决的抗滑问题，最终采用了这些概念中的一小部分，这是最关键的障碍之一(Nazir 1986; Forsberg 2001; Ruan et al. 2016).

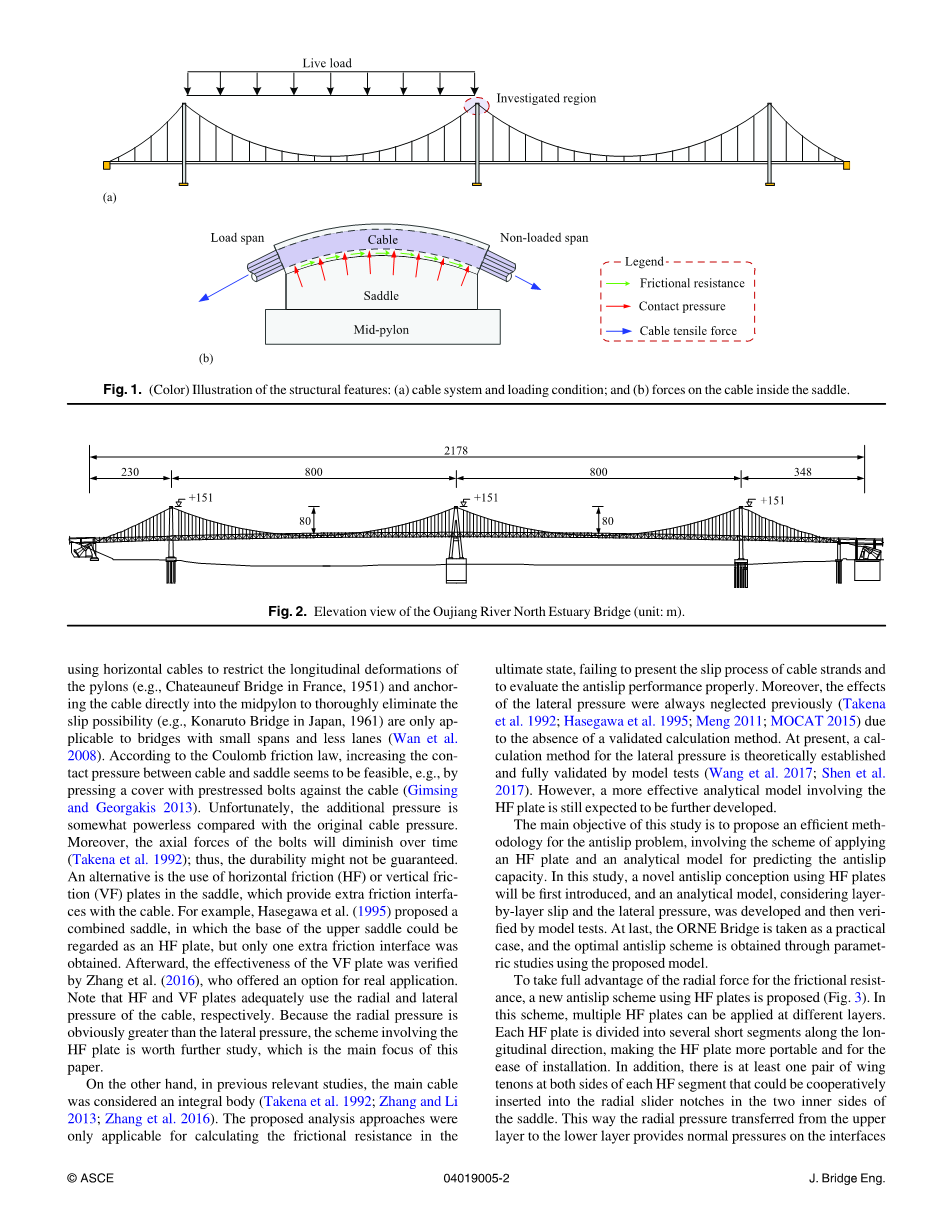
对于典型的多跨悬索桥（图1），当活荷载集中在其中一个中心跨度时，在中间塔的两侧之间引起主缆显著的不平衡拉力。由于主缆仅简单地位于固定在塔架顶部的鞍座上，因此纵向约束只能由摩擦阻力提供[图1（b）]。然而，传统鞍座提供的摩擦力通常太弱而无法抵抗不平衡力;因此，主缆产生滑动是可能的（Gimsing和Georgakis 2013）。于是，确保主缆的抗滑安全性是多跨悬索桥设计中的一大挑战。在中国的所有四跨悬索桥，即台州长江大桥（2012年），马鞍山长江大桥（2013年）和鹦鹉洲长江大桥（2014年），采用柔性钢结构，中间柱通过允许纵向变形可以减小不平衡力。然而，这却一定程度上牺牲了桥梁的垂直刚度和空气动力学稳定性，这也意味着一旦抗滑问题得到妥善解决，更加坚硬的中竿可能是更好的选择（Forsberg 2001; Jiang et al.2012; Wang et al。 2017年）。此外，这也可以应用于将来构造的跨度超过四个的悬索桥。

目前正在中国建造的瓯江北口（ORNE）大桥（图2）是一座四跨悬索桥，配有双层钢桁梁。上甲板和下甲板分别设计用于6车道高速公路和6车道I级公路。首先采用A形混凝土中梁，提高了驾驶舒适性，结构稳定性和经济性。然而，这种设计导致最大不平衡力达到35,811 kN，几乎是鹦鹉洲长江大桥（13,850 kN）的三倍。因此，提高主缆的摩擦阻力成为迫切需要解决的现实问题，还需要进一步开发有效的分析方法来预测改进措施的抗滑能力。

到目前为止，主缆和鞍座之间的摩擦系数几乎没有增加，因为两者之间的接触界面的性质基本上是定义的（Popov 2010）。使用水平主缆限制塔架纵向变形的方案（例如法国的Chateauneuf Bridge，1951）和将主缆直接锚固到中间塔以彻底消除滑移的可能性（例如，日本的Konaruto Bridge，1961）适用于小跨度和较少车道的桥梁（Wan et al.2008）。根据库仑摩擦定律，增加主缆和鞍座之间的接触压力似乎是可行的，例如，通过用预应力螺栓将盖子压在主缆上（Gimsingand Georgakis 2013）。不幸的是，与原始主缆压力相比，额外的压力有点无能为力。而且，螺栓的轴向力会随着时间的推移而减小（Takena等，1992）;因此，可能无法保证耐久性。另一种方法是在鞍座中使用水平摩擦（HF）或垂直摩擦（VF）板，这提供了与主缆的额外摩擦接口。例如，Hasegawa等人（1995）提出了一种组合式鞍座，其中上鞍座的底座可以看作是HF板，但只获得了一个额外的摩擦界面。之后，Zhang等人验证了VF板的有效性（2016），这为实际应用提供了的选项。注意，HF板和VF板分别充分利用主缆的径向和侧向压力。由于径向压力明显大于侧压力，涉及HF板的方案值得进一步研究，这是本文的重点。

图1. 结构特征图示：（a）电缆系统和负载条件; （b）在鞍座内的电缆上施加力

图2. 瓯江北口大桥立面图（单位：m）

图3. 使用水平摩擦片的防滑方案图示

另一方面，在以前的相关研究中，主缆被认为是一个整体（Takena等，1992; Zhang和Li，2013; Zhang等，2016）。所提出的分析方法仅适用于计算最终状态下的摩擦阻力，未能呈现主缆束的滑移过程并且正确地评估防滑性能。 此外，由于缺乏经过验证的计算方法，横向压力的影响以前总是被忽略（Takenaet al.1992; Hasegawa et al.1995; Meng 2011; MOCAT 2015）。 目前，理论上建立了横向压力的计算方法，并通过模型试验进行了充分验证（Wang等人，2017; Shen等人，2017）。然而，仍然期望进一步开发涉及HF板的更有效的分析模型。

本研究的主要目的是提出一种有效的解决抗滑问题的方法，包括应用HF板的方案和用于预测防滑能力的分析模型。在这项研究中，将首先介绍一种使用HF板的新型抗滑概念，并开发一种考虑逐层滑移和侧向压力的分析模型，然后通过模型试验进行验证。最后，以瓯江北口大桥为实例，采用该模型进行参数化研究，得到最优抗滑方案。

为了充分利用摩擦阻力的径向力，提出了一种使用HF板的新型防滑方案（图3）。 在该方案中，可以在不同层施加多个HF板。每个HF板沿纵向分成几个短段，使HF板更便携，便于安装。另外，在每个HF段的两侧存在至少一对翼榫，其可以配合地插入到鞍座的两个内侧中的径向滑块凹口中。这样，从上层传递到下层的径向压力在HF板的界面上提供了正常的压力，并产生了两个额外的摩擦力。因此，理论上有希望提高主缆和鞍座之间的抗滑能力。

2 分析模型

2.1力分布的推导

在本节中，理论上推导出电缆绞线和鞍座之间的径向和横向力，为下面的摩擦力计算提供了基础。如图4所示，具有初始轴向力T0的主缆支撑在鞍座上。当施加不平衡力△T时，引起两侧的缆索力的变化，即，在紧（t）侧和松弛（1）侧的缆索力分别变为和。考虑到中间塔的纵向变形，松驰侧（△）的缆索力的变化对于不同的桥通常不是恒定的。通过引入松散因子h来表达其变化

（1）

因此，两侧的缆索力可表示如下：

（2）

（3）

主缆的差分段在图4中给出。假设摩擦力保持与界面相切; 因此，径向上段的平衡方程由下式给出

（4）

其中=主缆和主缆之间的径向压力; R =鞍槽半径。

通过忽略二阶项,则（4）式将变成

（5）

原则上，是的函数（图4）。 为了简化这种情况，被假定为常数，就像中间的径向压力一样。 图4中的虚线表示出了总径向力可以等效地计算

（6）

其中=中间位置的径向压力; u =鞍槽的角度。

图4. 支撑在鞍座上的电缆的平衡状态

另一方面，由于鞍形槽的横向约束，股线产生横向压力。考虑到HF板，基于离散体之间的接触关系（Shen et al.2017; Wang et al.2017），可推导出横向力。考虑包含一个HF板和10股的典型鞍座，如图5（a）所示，通过HF板和间隔物分别将股线分成两层和三列。底部垫片固定在鞍座上，这是现实生活中的情况，而上部垫片由于结构上的困难和在实际情况下连接的可靠性差而不固定HF板。

图5. 侧压力的计算方法：（a）鞍座和钢绞线的沉降; （b）绞线的分隔; （c）力的传播; （d）不同钢丝的平衡状态。

选择底部中间链，即链1和2作为分析的实例[图5（b）]。 每根线被分成多条线，并且线的层数和线的列数分别为n和m。根据力和边界条件，每根钢丝的钢丝可以进一步分为七种，如图5的图例所示。此外，钢绞线2的钢丝可以分开，以清楚区分钢丝之间的接触力 [图5（c）]。因此，可以获得七种钢绞线的机械关系，并在图5（d）中示出。垂直和横向的平衡条件建立如下：

1.顶内钢丝

（7）

（8）

其中C1 =转换因子;=导线之间的摩擦系数; a = 是上下线之间的接触角; 和 =从第i层和第j列中的导线传递的法向力，在本研究中称为（i，j）导线，其左下方（i 1，j）导线 和右下（i 1，j 1）线; 和 =第g列中从顶部到底部转移到第j列的垂直力。在HF板下面的第一列（即Strands2-4），是来自上部股线的均匀分布的总压力。对于顶部HF板上的第一列（即，Strands8-10），显然为零，并且是自生成的径向力，其可以由近似方程（5）和（6）获得。

（9）

其中，和分别是在紧密和松散侧以及中心位置处的股线张力; 和=每股的线数。

2.顶端线

（10）

（11）

（12）

其中=柱中第g链的第i层线的横向力; =导线与侧面之间的摩擦系数; 和=另一个转换因子。

3.均匀层线

（13）

（14）

4.奇数层线

（15）

（16）

5.侧线

（17）

（18）

6.底部侧线

（19）

（20）

7.底内钢丝

（21）

根据公式（7）-（21），可以运用递归法获得同一列中每条链的横向力。因此，可以通过以下方式很容易地计算出钢绞线一侧的总横向力。

（22）

其中=计算列的链数。

类似地，鞍座中每个钢绞线柱的横向力可以从前面提到的推论中获得。需要注意的是，因为每个上部垫片的底部是不固定的，所以侧向力需要横向平衡，那么列之间就是相等的。因此，可以仅选择具有最大股数的中间柱来计算横向力。但是，对于底层的股线，因为底部垫片固定在鞍座上，每个柱的横向力应单独计算。如果有短导线用作绞线的填充物，则它们的自生垂直力应仅定义为零。

2.2 逐层滑动模型

在本节中，考虑到分层主缆，鞍座和配备的HF板，建立了逐层滑移过程的分析模型。 首先，做出以下三个假设：

1.假设股线的初始张力彼此相等，并且所施加的主缆的不平衡力均匀地分布在防滑股线中。

2.假设接触界面的静摩擦系数和动摩擦系数相等，这是相对安全的（Rabinowice1951; Popov 2010）。

3. HF板是无限刚性的，它的垂直运动是不受约束的; 因此，来自上层的径向压力可以完全转移到下层。

图6.（颜色）分析模型图示：（a）鞍座和主缆支架的布置; （b）股线的平衡力。

如图6所示，针对包含多个HF板的鞍座建立分析模型。假设HF板的数量为p，电缆束分为p 1层和q列。由于如前所述的上部和下部间隔物的约束条件的差异，同一层中的上部股线可以被认为是整体部分，而底部层中的股线应该被分别考虑用于不同的列。根据这种理解，主缆束的细分可以用矩阵表示

（23）

其中=第i（）层中的股数总数; 和=底层和第j列中的股数。

2.3 滑动力

为了呈现整个滑动过程，将不平衡力逐步施加到主缆上，直到所有股线滑动。假设在每个加载步骤中不平衡力具有的增量为，则可以从等式（2）和（3）推导出缆索力。如下：

（24）

（25）

其中和分别是在第k个加载步骤下松散侧和紧侧的索力。

为更加简化，参数后面的下标（i，j，k）表示第k个加载步骤下的第i层和第j列中的链。 在第一个加载步骤中，轴向力均匀分布，如表示的那样

（

英语原文共 15 页

资料编号：[3867]