英语原文共 25 页，剩余内容已隐藏，支付完成后下载完整资料

一个新的抛物线变分不等式拟合的Signorini条件非稳定渗漏问题与复杂的渗流控制系统

摘要

通过将达西定律扩展到自由表面以上的干域，并将潜在渗流表面上的边界条件指定为Signorini类型，在整个关注区域中定义的偏微分方程（PDE）被制定为非稳态渗流问题，自由表面。然后提出一个等价于PDE公式的新的抛物线变分不等式（PVI）公式，其中PDE公式中的Signorini类型的互补条件的通量部分被转换为自然边界条件。因此，消除了渗出点处的奇点，并且显着减少了选择试验功能的难度。通过在有限元分析中引入自适应的惩罚Heaviside函数，离散PVI公式的数值稳定性得到了很好的保证。提出的方法通过现有的水头突然上升和下降的实验室测试验证，然后应用于在上游水头的线性下降期间捕获具有五个排水隧道的均匀矩形坝中的非稳定渗流流动行为。水库河水电工程地下厂房周围岩石的不稳定渗流进一步模拟，涉及复杂的渗流控制系统。与在现场监测数据比较表明，该计算结果以及示出了非稳定渗流蓄水期间以及过程的储层的操作的排水孔列和排水通道的防渗效果。版权2010 John Wiley＆Sons，Ltd

2009年11月3日收到; 2010年3月30日修订; 接受2010年4月8日

关键词：不稳定渗流; 变分不等式; Signorini的条件; 自由表面; 渗流控制; 数值模拟

1. 引言

描述重力水的运动以及由于水位的波动而导致的介质中水的释放或储存。与饱和/不饱和渗流分析相比，另一方面，虽然它不能捕捉毛细作用和其他形式的地下水的运动，但它避免了在保水曲线和其他不饱和性质的测定中的困难。因此，非稳定渗流分析仍广泛应用于工程实践，特别是在地下岩石工程中，其中不饱和行为对周围岩石的稳定性影响较小，描述重力水的运动和水的释放或储存在介质中由于水位的波动。与饱和/不饱和渗流分析相比，另一方面，虽然它不能捕捉毛细作用和其他形式的地下水的运动，但它避免了在保水曲线和其他不饱和性质的测定中的困难。因此，非稳定渗流分析仍然广泛应用于工程实践，特别是在地下岩石工程中，不饱和行为对周围岩石的稳定性影响较小

非稳态渗流问题不同于其稳态渗流问题，因为前者涉及随时间变化的自由表面（或传播前沿），但类似地，它涉及一组在数学中是奇异的渗流点，导致 强非线性的问题。 因此，非稳态渗流分析的主要任务是随着时间的推移定位自由表面和渗流点。 为此，在文献中提出了在有限元中具有固定网格的直观方法[1-4]和变分不等式方法[5-13]。

直观的方法包括调整渗透率方法[1]，残余流方法[2]和初始或虚拟流方法[3,4]等，他们通常涉及启发式迭代程序在每个时间步骤，以确保 干域中的流量在幅度上与湿域中的流量相比是可忽略的。 另一方面，变分不等式方法在数学中更加严格，并且它们总是通过在固定域中定义新的初始边界值问题将传播前沿变换为内边界[6,10]。

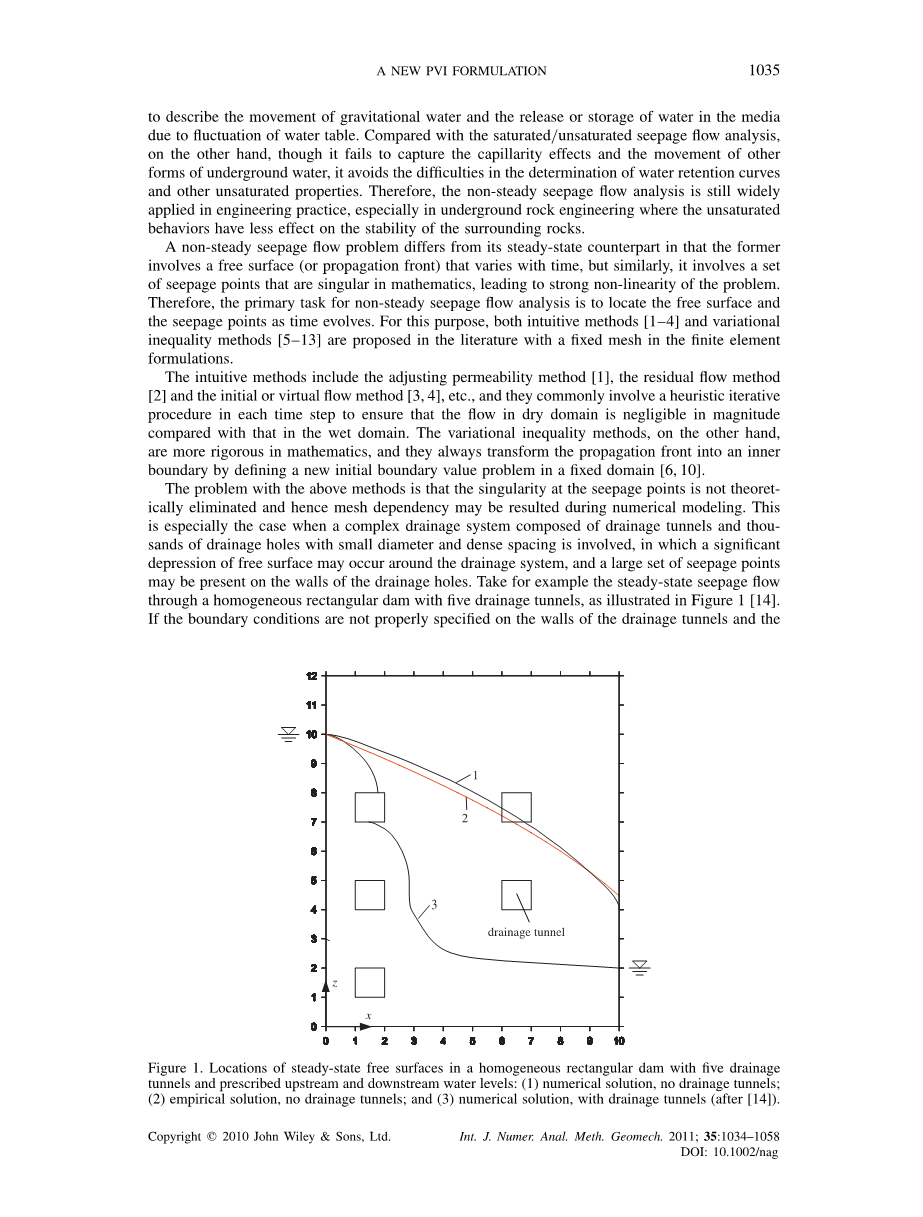
上述方法的问题在于渗流点处的奇异性在理论上没有被消除，并且因此在数值建模期间可能导致网格依赖性。当涉及由排水隧道和数千个具有小直径和密集间距的排水孔组成的复杂排水系统时，尤其是这样的情况，其中在排水系统周围可能发生显着的自由表面凹陷，并且大的渗透点可存在于排水孔的壁上。以稳态渗流为例，通过一个具有五条排水隧道的均匀矩形坝，如图1所示[14]。

如果边界条件没有在排水隧道的墙壁上适当规定，图1稳定自由表面在具有五条排水隧道和规定的上游和下游水位的均质矩形坝中的位置：（1）数值解，无排水隧道;（2）经验解，无排水隧道;和（3）数值解，带排水隧道（在[14]之后）在渗透点的奇异性在问题陈述中没有克服，严格收敛解将不可用，即使这样一个简单的例子。

为了减少与大量一维延伸排水孔相关的网格生成的难度，文献中提出了大量的建模方法，包括等效介质方法[15]，子结构技术[16,17] 分析方法[18,19]，点井模型[20]和复合元素方法[21]等。然而，大多数现有模型（除了子结构技术），或多或少地精确地描述细节 排水孔的边界条件，从而在一定程度上牺牲了解的理论严格性[14]

对于稳态渗流问题，郑等 [22]通过将湿域中定义的传统达西定律扩展到整个感兴趣的领域，并指定潜在渗流表面的边界条件作为Signorini类型的互补条件，提出了椭圆变分不等式公式。 这种公式理论上消除了渗透点处的奇异性，并有效地克服了得到的网格依赖性和数值不稳定性。 在此基础上，Chen et al。 [14，23]提出了一种将变分不等式与子结构技术和自适应惩罚性海维赛函数相结合的方法，已成功应用于解决大坝工程中复杂排水设施的一些具有挑战性的稳态渗流问题。

通过将我们以前的工作扩展到不稳定的渗流问题，在本研究中提出了一种新的抛物线变分不等式（PVI）公式。证明了PVI制剂与在整个范围内定义的偏微分方程（PDE）制剂之间的等效性，并且建议用于PVI制剂的有限元实施的数值方法。由于潜在渗流表面上的Signorini型互补条件的通量部分被转换为PVI公式中的自然边界条件，消除了渗流点处的奇异性，并且在数值模拟期间选择试验函数的难度显着减少。通过在有限元分析中引入自适应的惩罚Heaviside函数，离散PVI公式的数值稳定性得到了很好的保证。所提出的方法通过由Akai等人进行的实验室测试来验证。 [24]，并用于捕获具有五条排水隧道的均质矩形坝的非稳定渗流行为。本研究进一步模拟了在中国水布亚水电项目中采用复杂渗漏控制系统的地下储库周围岩石储层积累和作业引起的不稳定渗流过程。

在该研究中还显示，上述PVI制剂可以简单地降低至其稳态对应物，即Zheng的制剂[22]。 在减小的稳态中为自由表面建立两个几何性质，这可以作为判断数值解是否严格收敛和理论上合理的直观标准。

本文的其余部分安排如下：第2节通过将达西定律延伸到干域，在整个领域中制定PDE形式的自由表面的不稳定渗流问题，以及Signorini对潜在渗流边界的条件规范 。 还提出了自由表面的稳态渗流问题的几何性质。 在第3节中，提出了PVI制剂，证明了PVI和PDE制剂之间的等效性。 在第4节中，描述了PVI公式的数值实现和验证。 第5节介绍了将拟议模型应用于具有复杂渗漏控制措施的地下发电厂，之后是第6节中的结论性意见。

1. 稳定/非稳定渗流问题

如图2所示，通过区域M的非稳态渗流实际上是通过低于自由表面F f的湿区域M w的流量。 只要自由表面F f定位，在时间t的湿域Mw将被确定，这显然是预先未知的。为了在整个域M上定义新的初始边界值问题，如PVI公式所要求的，达西定律被重新定义如下[14,22]：

v(t )= minus;knabla; $(t ) v0(t ) （2）

其中v是流速，v0是初始流速，k是二阶水力传导张量，$ zp /（qwg）是总水头，z是垂直坐标，p是孔隙水压力，qw是水的密度 g重力加速度。 这里，引入v0以消除干燥区域Md上的虚拟流速，形式为

v0(t )= H ($minus; z)knabla; $(t )

其中H（$ -z）是Heaviside函数

（3） 通过引入关于变形固体骨架的材料衍生物的定义

(4)

通过整个区域M（M Mw Md）的渗流然后由以下连续方程控制：

d{[1minus; H ($minus; z)]nqw} [1minus; H ($minus; z)]nqnabla;· vs nabla; · (qv)= 0 (in M) (5)

dt

w

其中vs是固体骨架的速度，n是介质的孔隙率。

假设固体骨架是不可压缩的，固体骨架的质量守恒导致

dn

dt =(1minus; n)nabla;· vs (6)

此外，对于不可变形的矩阵，有效应力原理可以表示为

dr=drrminus;dpd (7)

其中r和rr分别是总和有效应力张量，d是Kronecker delta张量。

在没有明确建模介质的机械响应的情况下，可以假设以下关系用于表征渗流对固体变形的影响：

(8)

3

考虑到地下水的压缩性，有

dqw

q =thorn;wdp=thorn;wqwgd$ (9)

w

其中thorn;w是水的压缩系数。

通过在自由表面F f，f f上定义Dirac delta函数，等式（3）中的海维赛德函数的导数可以表示为

dH=minus;amp;Ffd$ (10)

其中F f（x，y，z）$ z是自由表面，M w（x，y，z）z“和M d（x，y，z） 在图2中，时间t t0处的F f AE，t t0 At处的F f ArEr和t t处的F f KD。 由于等式（3）以其在数学中的原始定义的互补形式定义的事实，引入等式（10）中的负号。
假设所考虑的介质的骨架由于渗流运动而经历小的变形，我们有

(11)

其中thorn;s和εv分别是介质的体积应变和体积应变。
将等式（6）和（8） - （11）代入等式（5）中得到质量守恒方程
的地下非稳定渗流

(12)

其中Ss qwg（thorn;snchi;w）是介质的特定存储。
在式（12）中，第一项考虑了由于地下水位的波动而导致的湿域Mw和干域Md之间的水交换。 然而，在多孔介质中，由于在毛细管水和薄膜水形式的孔中保留水，在吸引过程期间的水存储的体积分数或在排水过程期间的水释放总是小于孔隙率n。 为了解释这种效应，在该项中优选重力比产率mu;（mu;Mn）而不是n。 因此，等式（12）可以重写为

(13)

连续性方程式（13）经受以下初始条件：

$(x, y, z; t )|t =t0 = $0(x, y, z) (inM) (14)

和以下边界条件：
bull;水头边界条件

$(t )= $macr; (t ) (on F$) (15)

其中$是F $上的规定水位。 如图2所示，F $ = AB CD with
分别在下游表面CD上的上游表面AB和$macr;macr;d上，在时间t= t0和F $ =BK CD在t= t。

bull;通量边界条件

qn(t ) equiv;minus;n· qwv(t )= qmacr; (t ) (onFq=BC) (16)

其中qmacr;是Fq上的规定磁通，n是边界的外向单位法向量。 对于不可渗透的边界，qmacr;= 0。

bull;Signorini型在渗流面上的边界条件[14，22]

lt;

全文共18913字，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[145032]，资料为PDF文档或Word文档，PDF文档可免费转换为Word