英语原文共 16 页，剩余内容已隐藏，支付完成后下载完整资料

在单调和循环荷载下CFRP约束混凝土轴向应力-应变模型

Najwa F. Hany¹；Elie G. Hantouche，A.M.ASCE²；Mohamed H. Harajli³

摘要：本文给出了18个碳纤维增强聚合物（CFRP）约束的圆形、方形和矩形柱样本在循环轴压作用下轴向应力-应变的实验结果，并对实验结果进行讨论。根据这些实验结果和来自在其他技术论文中报道的测试数据的指导下，建立了广义荷载条件下CFRP约束混凝土的轴向应力-应变基本模型。所提出的模型由单调包络响应和循环响应组成，这个模型广泛的参考了实验参数，采用了比现有论文中所使用模型更加简化的方法。该模型覆盖了所有重要参数，并且预测了峰后响应的上升和下降。模型除了应用简单，而且误差还小，该模型可以以较高的精度贴合实验中测得的测试结果和来自在其他技术论文的报道的测试数据。该模型可用于预测基于CFRP约束的循环响应的混凝土结构构件循环响应的数值分析方案。

DOI:10.1061/(ASCE)CC.1943-5614.0000557.copy;2015AmericanSocietyofCivilEngineers.

关键词：混凝土；柱；约束；循环荷载；纤维增强聚合物；应力-应变模型

1. 引言

已经进行了许多实验和分析研究，以评估由碳钎维增强聚合物(CFRP)板约束下混凝土柱的应力-应变响应。这些研究已经清楚的表明，CFRP护套的约束会有效改善混凝土柱的轴向强度、延性以及能耗特性。这些实验大多集中在受单调荷载作用下CFRP约束混凝土试件上。最近的这些研究包括Lam和Teng (2003a,b),Harajli等人.(2006),Rousakis等人.(2007),Youssef等人.(2007),Ilki等人.(2008),Eid和Paultre (2008),以及Csuka和Kollar (2010)。

但是只有几项实验研究关于在循环荷载作用下FRP约束混凝土试件的实验被发表。（Lam等人.2006，2009；Wang等人2012a，b，c；Abbasnia和Holakoo.2012；Abbasnia等人2013）在这些研究中，Lam等人（2006）对CFRP约束圆形截面混凝土试件进行了单调循环加载实验。Lam和Teng（2009）使用了循环加载试件实验的实验结果同以前的研究结果，提出了新的表达式来体现混凝土柱不同时期的循环响应。Wang等人（2012b，c）通过他们的实验，开发出两种大截面FRP约束混凝土循环轴向应力-应变模型，一种为方形截面，一种为圆形截面。Abbasnia等人（2012a，b）进行了一个实验研究，研究约束强度，长宽比，无约束混凝土抗压强度和拐角半径等参数对循环荷载下FRP混凝土的性能的影响。这些研究主要集中在对塑性应变和应力下降的影响评估。Abbasnia等人（2012a，b）得出结论在没有侧向约束的情况下塑性应变随着混凝土强度增加而减小，但是强度的降低与参数无关。Ozbakkaloglu和Akin（2012）进行了一项实验，以评估单调循环轴向加压下受到AFRP和CFRP约束的普通混凝土（NSC）和高强混凝土（HSC）圆柱体的响应。在相同的约束条件下，NSC的强度和应变增量比HSC更明显。他们的研究还表明，约束混凝土柱的塑性应变和约束强度和FRP种类无关。但是，与Lam（2009）和Abbasnia等人（2012a）的结论相反，无约束混凝土对塑性应变的影响可以是忽略不计。

大多数文献中报告的可以采用的轴向应力-应变模型的都考虑的情况下，FRP提供的约束强度导致混凝土极限强度提高，进而导致峰后上升的情况。但是还有少数模型预测混凝土在约束强度较低的情况下会产峰后下降的情况。此外，此前没有没有关于文献描述FRP约束矩形截面循环应力-应变响应的模型。因此，需要提出一个新的模型来预测CFRP约束混凝土的循环响应，囊括不同截面形状和约束水平，导致峰后应力-应变下降情况。

在这次实验中对18个不同截面（圆形、正方形、矩形）的CFRP约束混凝土试件进行了循环轴压试验。作为本次实验的实验的一部分成果和其他技术论文实验方法的实验结果一同被用于开发一个新的广义荷载条件下CFRP约束混凝土的轴向应力-应变基本模型。该模型涵盖了最常见的混凝土类型，即圆形、正方形、矩形，并考虑了CFRP约束的强弱水平。

1. 实验程序
   1. 实验参数及实验样本

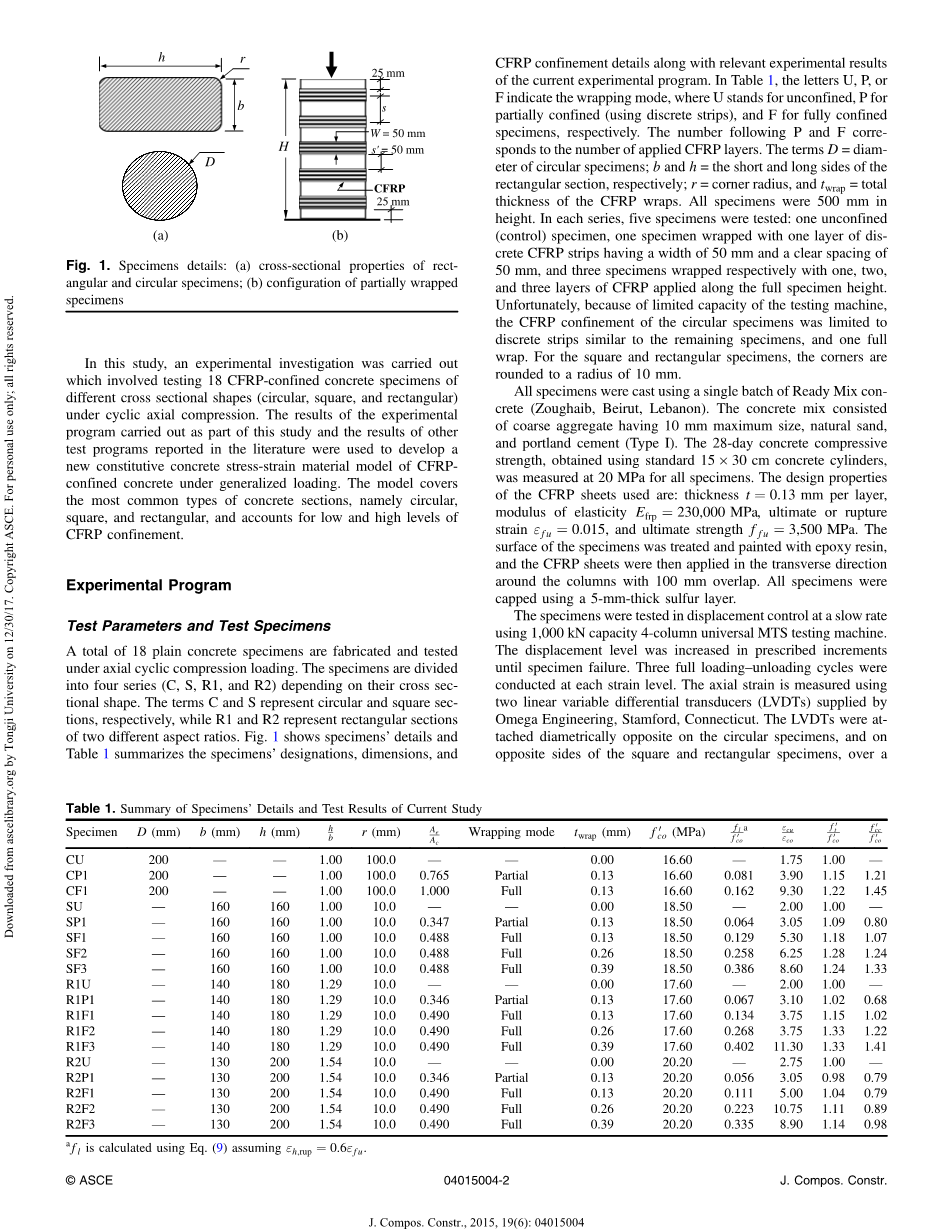
制造了18个素混凝土样本，并对其进行轴向循环加压实验。根据横截面形状，将试件分成四组（C、S、R1和R2）。C组和S组分别表示圆形截面和正方形截面，而R1和R2表示两个长宽比不同的矩形。图一为试件详图，表一为试件名称、尺寸、CFRP约束情况，以及在此条件先得到的相关实验的结果。在表一中，U、P、F代表着约束情况，U代表着无约束，P代表着部分约束（使用离散条），F代表着完全约束。P和F后面数字代表着碳钎维的层数。D=圆形样本试件的直径；b、h=矩形截面短边、长边尺寸；r=边角半径；t_wrap=碳钎维的厚度。所有样本高度均为500mm。在每组中五个样本进行实验：一个无约束（对照）样本；样本用一层CFRP包裹，宽度50mm，净间距50mm；另外三个样本分别用一层、两层、三层的CFRP覆盖全样本高度。不幸的是，由于测试机器能力限制，圆形样本的CFRP约束仅限于与其样本相同的离散条，以及一个一层全包。正方形和矩形样本，边角圆角半径为10mm。

所有样本使用的是同一批预制混凝土（黎巴嫩贝鲁特Zoughaib）制作。混凝土由最大粒径为10mm的粗骨料、天然砂、硅酸盐水泥（Ⅰ型）组成。所有样本在28天混凝土抗压强度为20MPa，采用15*30cm标准混凝土圆柱体。采用CFRP材料设计特点为：每层厚度t=0.13mm弹性模量E_frp=230，000MPa极限应变ε_fu=0.015极限强度f_fu=3500MPa。对样本表面处理后涂上环氧树脂，然后将CFRP布以100mm距离横向包裹柱。所有样本均用5mm后硫层包裹。

用强度为1000KN的四柱完能MTS试验机，对样本进行缓慢的应变测试。应变等级以规定的量增加，直到样本被破坏。在每个应变强度上进行三次完整的加载-卸载的循环。轴向应变测量使用两个由康涅狄格州斯坦福德欧米茄工程公司提供的线性可变差动传感器（LVDT）。如图二所示，LVTD分别贴在圆形样本、方形样本、矩形样本两侧在柱中部区域长度250mm。样本全长上的平均应变（标准长度=500mm）也可以使用两个完整的在两侧的LVDT测量（图二）。混凝土侧向应变是使用两个5mm长的电应变片（也是欧米茄工程公司提供）安装在CFRP包裹的中间高度。应变片在圆形样本上相隔180°，在方形和矩形放置在两个连续侧面上。对于方形样本，使用两个长度为160mmLVTD分别在样本两侧面，测量侧面平均横向应变。对于矩形样本，两个LVTD分别横向安装在样本连续的侧面，R1组长度分别为140mm和180mm，R2组为130mm和200mm。

• 1. 实验结果

图三（a和b）分别为有约束样本和无约束样本典型破坏模式。对于无约束样本，破坏是由于混凝土被完全压碎产生的。对于有约束样本，破坏是由于CFRP被压坏，导致荷载抵抗力突然下降。对于方形和矩形样本，CFRP破坏发生在边角处。图四（a和b）为C和S组中所有混凝土样本轴向应力-应变响应，图五（a和b）中，为R1和R2两个实验组样本数据。

• • 1. 包络响应

图六显示了理想化下样本应力应变响应。与包络曲线相关的测试结果汇总在表一中。表中f^rsquo;_t应变ε_c接近或略高于0.002时，应力-应变响应第一个峰值的混凝土应力；ε_cu为CFRP发生破坏时混凝土的极限应变；f^rsquo;_cc是对应ε_cu的混凝土极限强度。

所有无约束样本，峰值应力对应轴向应变为0.002时。无约束样本峰值应力为：圆形样本CU最大应力为16.6MPa，方形样本SU最大应力为18.5MPa，矩形样本R1U最大应力为17.6MPa，矩形样本R2U最大应力为20.2MPa；这些实验结果大多略低于圆柱形混凝土20MPa抗压强度。

对于CFRP约束样本，他们的包络应力-应变响应应具有三个阶段特点，这是技术论文里面写道的关于CFRP约束混凝土典型响应。

在第一阶段的响应与无约束样本应力-应变曲线的上升分支吻合。由于混凝土膨胀，FRP约束将在接近0.002轴向应变的时候产生；根据FRP的面积以及样本的截面形状和尺寸，曲线第二分支可以是上升的也可以是下降的。最终应力f^rsquo;_cc和应变ε_cu的样本破坏意味着FRP的破坏并且开始第三阶段轴向荷载突然下降。在表现峰后上升的样本中，圆形样本部份或者完全在于第一层CFRP（CP1和CF1），而R1组和方形样本（SF3和R1F3）约束在第三层CFRP。对于其余样本，CFRP提供的约束改善了峰值时候的轴向强度，但也导致了峰后下降的情况。对于有约束的样本，第一阶段峰值应力f^rsquo;_t和极限轴向强度f^rsquo;_cc的改善超过了对无约束混凝土抗压强度f^rsquo;_co使用比例评估f^rsquo;_t/f^rsquo;_co和f^rsquo;_cc/f^rsquo;_co列在表一中。从图四和图五以及表一中可以看出，CFRP的约束极大的提高了极限轴向应变ε_cu数值。但是，截面形状对极限轴向应变的影响不如对轴向强度的影响明显。

• • 1. 循环响应

理想化循环响应如图六。图四和图五的结果表明，一个完整周期的循环响应应有两个明显且有明确界定的路径组成：（1）曲线卸载路径，特征是坡度逐渐减小，直到它与应变轴线相交，在本研究中称它为包络塑性应变ε_pl，evn（2）一个几乎线性重新加载路径，与包络曲线相交在（ε_ret，sigma;_ret）。

从图四和图五的循环响应中可以得到的观察结果，对于本研究提出轴向应力-应变模型（图六）有促进作用，观察结果如下：（1）在包络塑性应变ε_pl，evn的强度下，循环响应的固有形状与样本横截面无关；（2）由于混凝土劣化，塑性应变ε_pl，evn和包络卸载应变ε_un，evn差会变大随着包络卸载应变ε_un，evn增大，将导致应变能吸收和耗能增大；（3）随着循环次数的增加，重新加载路径的强度会略微下降。Abbasnia等人（2012a，b，2013）之前已经研究过循环响应对于横截面形状（拐角半径和长宽比）的联系，并且发现卸载/重载曲线的固有形状不受横截面形状影响。至于塑性形变ε_pl，evn与卸载应变ε_un，evn变化几乎所有早期研究（例如：Lam等人2012a，c；Abbasnia和Holakoo2012;Abbasnia等人2012a, b, 2013; Ozbakkaloglu和Akin2012）都是呈现线性增加的关系，与第二个实验结果一致。重载循环中应力降低与Lam等人（2006）Abbasnia和Holakoo(2012), Abbasnia等人(2012a，b)的研究一致。还要注意，对于同一周期的塑性应变ε_pl，evn卸载应变ε_un，evn随循环次数的增加而略有增加，这也被其他科研人员记录过（Lam和Teng2009；Abbasnia等人2012b）。尽管如此但是，在建立循环荷载作用下的应力-应变响应理论模型时，认为相应的增量较小，可以忽略不计。

1. 广义应力-应变模型

为了更好的预测FRP约束混凝土在广义荷载作用下应力-应变响应，提出了一种基本模型。图6中理想化模型，除了根据当前实验的测试结果和来自其余技术论文中的其他测试数据对特征参数进行了完善，还采用现有的预测模型。所提出的模型适用于包括圆形、正方形和矩形在内的常见截面类型，并且能够预测低或中等约束情况下可能导致峰后软化和下降的情况。

• 1. 包络单调响应 剩余内容已隐藏，支付完成后下载完整资料

     ---

     资料编号：[261818]，资料为PDF文档或Word文档，PDF文档可免费转换为Word