英语原文共 14 页，剩余内容已隐藏，支付完成后下载完整资料

基于模糊逻辑的摩托车牵引力控制系统的进化优化

摘要——制动与牵引控制系统是车辆安全的基本设备。第一个功能是当汽车紧急制动时，防止车轮抱死。第二个功能是当过多的扭矩被应用于驱动轮时防止车轮打滑。本研究的目的是制定和实施一个安装在摩托车上的新的牵引力控制系统，调节牵引滑动和改善双轮车辆的动态行为。本文提出了一种新的牵引力控制算法，它利用了模糊逻辑控制块。执行了双策略创造出的控制块。在第一条策略中，根据经验对模糊逻辑控制器进行参数调整。在第二条策略中，利用进化算法获取参数以增强牵引力控制器。已经证明，进化算法的应用可以改善模糊逻辑控制算法，获得的结果比那些仅仅依靠经验的控制取得的结果更好。

关键词：术语—进化计算，模糊控制，牵引力控制系统（TCS），汽车安全

一．简介

防抱死制动系统和牵引力控制系统的出现已经成为车辆安全中的重要发展。这些系统自从他们出现便一直在进化，始终保持相同的目标，但是使用的是日益复杂的算法和复杂的制动和转矩控制构架。它已经成为与其他安全功能一起工作的系统。

这些系统最先安装在四轮汽车上，在两轮汽车上安装、使用它们更加复杂。然而，我们对在摩托车上发展和实施这些系统有强烈的兴趣，特别是在提高这些车辆的主动安全性方面[1]。虽然防抱死制动系统被广泛应用于两轮汽车，但是很少在摩托车上尝试安装个使用牵引力控制系统。例如，在[2]，提出了牵引力控制系统应用于线性运动的摩托车。提出了一个二阶滑模控制。控制器以电子油门的位置作为控制变量。在[3]中介绍了低消耗并且安装了牵引力控制的摩托车。控制是利用前后轮速度差异进行的。同样地，牵引力控制系统采用模糊滑块控制提出了[4]的一个直接驱动的电动滑板车。另一个工作是讨论摩托车发动机滑动力学的牵引力控制设计[5]。最后，一个完整的方案与框架表示牵引力控制系统中元素与参数之间的关系，如[6]所示。

另一方面，许多关于两轮车辆的制动控制系统的研究已经进行。在[7]中，研究了一种用于两轮车辆的电动前轮制动的线性参数变差控制方法。在[8]中介绍了拥有防抱死制动系统、使用单通道交流驱动器的轻型摩托车的发展。最终，防抱死制动系统用于摩托车的前期工作在[9]中实现。

控制算法是牵引力控制系统和防抱死制动系统的必要部分。新算法的研究对汽车动力学研究有极大好处，已经有大量的论文聚焦这个话题。由于设备制造商对控制算法的绝对保密，从用户的角度来看，作为一个“黑盒子”，它需要利用每个车轮的角速度和其他方法保持稳定性和牵引力的控制作为输入，并且拥有必要的动作作为输出。目前，控制模型的发展主要是基于允许在不同条件下，摩托车车手手动执行制动或者加速的适应性调整技术。

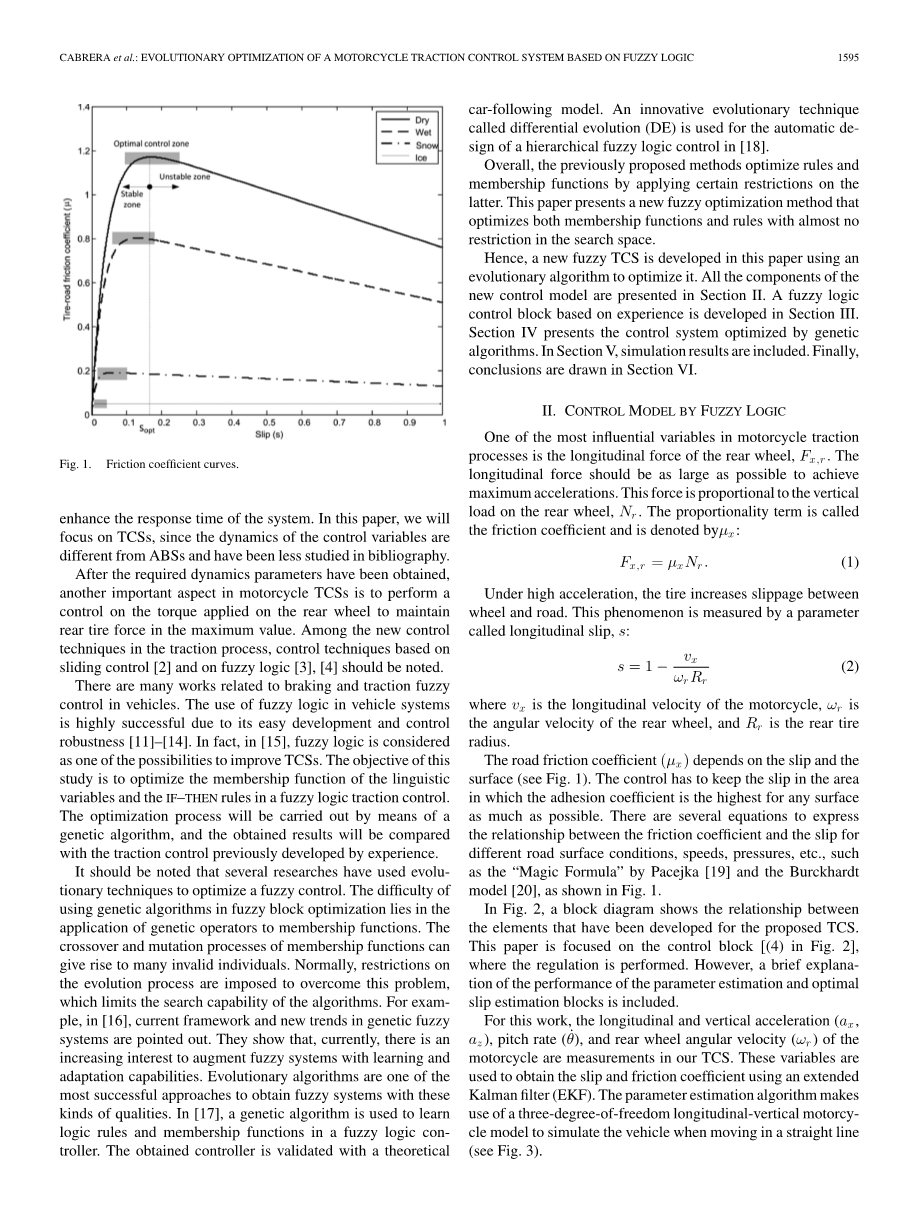
这些系统的主要问题是确定最佳轮胎-路面摩擦曲线（见图1）以确定滑移率（s）和摩擦系数（mu;），以此获得在摩托车在制动、牵引过程和转弯时的稳定性。在牵引或制动过程中所设计的摩擦系数和滑动的曲线是相似的（见图1）。牵引力控制系统和防抱死制动系统的目的是尽可能保持滑移率在最优控制区域内，表明其特征的最大允许摩擦系数我们在图1中可以观察到。当滑移率超过产生最大摩擦系数时的滑移率，纵向和横向的轮胎承受力急剧下降。牵引力控制系统和防抱死制动系统发展中的障碍之一是对不同的轮胎类型和路面条件的车轮滑移率与附着系数特征的实时估计[10]-[12]。

图1 摩擦系数曲线

牵引力控制系统和防抱死制动系统的区别在于控制的动态过程。第一个系统（牵引力控制系统）使用制动转矩作为控制变量，第二个系统（防抱死制动系统）使用牵引转矩作为控制变量。一些牵引力控制系统也可以使用后制动和牵引力转矩提高系统响应时间精确度。在本文中，我们重点关注牵引力控制系统，因为其控制变量的动态过程不同于防抱死制动系统且目前应用较少。

获得动态参数后，摩托车牵引力控制系统的另一个重要方面是对后轮施加转矩控制，以确保后轮承受力维持在最大值。在牵引过程中的新控制技术中，基于滑动控制[2]和模糊逻辑控制[3]、[4]应引起注意。

有许多问题与车辆制动和牵引模糊控制相关。模糊逻辑在车辆系统中的应用是非常成功的，因为它容易发展并且具有控制的鲁棒性[11]-[14]。事实上，根据[15]，模糊逻辑可以提高牵引力控制系统性能。这项研究的目的是优化语言变量的隶属函数和模糊逻辑牵引力控制中的IF-THEN规则。优化过程将利用遗传算法，所获得的结果将与以前基于经验的牵引力控制系统比较。

应该指出的是，一些研究已经使用进化技术来优化模糊控制。在模糊块优化中使用遗传算法的难点在于遗传因子在隶属函数中的应用。隶属函数的交叉和变异过程能够引起许多无效的个体。通常，限制进化过程是为了克服这个问题，但这也限制了算法的搜索能力。例如，在[16]中指出的目前遗传模糊系统的新趋势。他们表明，目前，研究人员对增加模糊系统的学习能力和适应能力越来越有兴趣。进化算法是用以获得这类模糊系统的成功方法。在[17]中介绍到，遗传算法是用来学习逻辑规则和模糊逻辑控制器的隶属函数。获得的控制器经过了理论汽车模型的验证。一种被称为差分进化(DE)的进化技术适用于自动模糊逻辑控制，在[18]中有所介绍。

总而言之，通过对以前提出的优化规则和隶属函数施加一定的限制得到后者。本文提出了一种新的模糊优化方法，不仅优化了两个隶属函数和规则，而且几乎没有限制搜索空间。

因此，一种新的使用进化算法优化的模糊牵引力控制系统被提出。第二节介绍了新的控制模型的所有组件。基于经验的模糊逻辑控制块在第三节中介绍。第四节介绍了遗传算法优化的控制系统。第五节介绍了仿真的结果。第六节中得出最后的结论。

二．模糊逻辑控制模型

摩托车牵引过程中最有影响的变量之一是后轮的纵向力， F_{x ,r} 。纵向力应该尽可能大，以达到最大加速度。这种力与后轮的垂直载荷成正比，N_r 。这个术语称为摩擦系数，并且表示为mu;_x。

在高加速度下，车轮和路面之间的滑移率增加。这种情况由一种叫做纵滑移率的参数确定，s:

公式中v_x 是摩托车的纵向速度，omega;_r是后轮角速度,R_x是后轮胎半径。

路面的摩擦系数（mu;_x )取决于表面情况（见图1）。控制必须保持表面粘附系数最高区域的滑移率不变。有几个方程来表示在不同的路面条件、速度、压力情况下的摩擦系数和滑移率之间的关系。例如Pacejka [19]中的“魔术公式”和Burckhardt[20]中的模型，如图1所示。

在图2中，方框图显示了牵引力控制系统的要素之间的关系。本文的重点是可进行调节的控制块[图2（4）]。简单解释了参数估计和最佳滑移率估计块的性能。

对于这项工作，在于我们的牵引力同步控制系统中纵向和垂直加速度（a_x,a_z），俯仰角速度和后轮角速度omega;_r测量。这些变量利用扩展卡尔曼滤波器（EKF）来获得滑移率和摩擦系数。参数估计算法利用三自由度纵向自由垂直摩托车模型来模拟车辆的直线运动（见图3）。

图2 牵引力控制系统框图

图3 摩托车模型

用于估计的模型来自刚体动力学方程。这些方程是：

公式中M是摩托车的质量；a_x和v_x分别是纵向加速度和速度；a_z、v_z和z分别是垂直加速度、速度和位移；和分别是加速度和速率。F_{x ,r} 是后轮的纵向力（见图1），F_{x ,f}是滚动阻力，C是气体阻力系数。N_f和N_y分别是前轮和后轮上的垂直载荷，I_y是穿过质心的转动轴转动惯量。最终地，l_f和l_r分别是前轮和后轮的半长。滚动阻力被认为如下：

其中C₁和C₂是常数。

一种基于EKF的参数估计块是用来确定滑移轮胎-道路摩擦系数所必需的纵向速度和其他参数。EKF采用以下系统：

式中w_k和v_k分别代表模型中的噪声和观测，x_k是状态变量向量，y_k是测量向量。

使用动态方程表示涉及执行估计变量措施的状态变量和方程是必要的。状态变量向量是，测量向量是，一个被称为“随机行走”的动态模型已被用于估计F_{x ,r}、N_r和N_f [21]。一个摩托车纵向动态有限差分方程被用来估计摩托车纵向速度，即v_x 。因此，状态变量向量的动态方程，如图（9）所示。

离散型方程组与状态变量向量的关系：

因此，EKF算法需要估计垂直力、纵向力和速度。有了这些估计值，我们就可以得到每一时间步的滑移率和摩擦系数：

我们已经估计了滑移率（s）和摩擦系数（mu;_x），模糊神经网络模块用来获取最佳滑移率（s_opt），即摩擦系数最高表面对应的滑移率（见图1）。这个阶段包含在图2中的方块3中。

为了实现目的，第一阶段用于计算道路类型。在这一阶段，我们使用模糊逻辑识别块。这种逻辑模糊识别块在[11]中有解释。其次，逻辑模糊识别块的输出用于获取最佳滑移率（s_opt）。我们提出的神经网络由三层组成。前两层有“对称型”激活功能，最后一层为“线性”型。神经网络的输入是道路类型、附着系数（mu;）和滑移率（s），输出是一个表示摩托车在道路上的最佳滑移率（s_opt）的值。要知道适当的重力和偏差才能进行神经网络训练。这将需要一系列的道路类型参数、附着系数和最佳滑移率。依靠这些输入值对重力和偏差进行调整。因此，输入是估计的滑移率（s）和最佳滑移率（s_opt），输出是减小油门（TR）。

本次研究的目的是利用经验通过增强控制器发展模糊控制块，最终提高牵引力控制系统的性能。基于模糊逻辑的控制技术被用于非线性控制系统。

模糊逻辑处理器是比较容易实现的；因此，这种技术的使用已经得到了扩展。此外，操作控制过程类似于人类的直觉，它允许引入专家知识。我们必须考虑到我们所从事的工作是非线性的并且是非常复杂的。正是由于这样的事实，牵引力控制系统需要控制后轮转矩或者油门，最终实现减少滑移率。然而，仅仅能够在不考虑驱动和滑移率间所有因素的变化时，才能在复杂的模型中应用。因此，我们必须以基于专家知识的控制为基础。

我们的模糊控制是输入为滑移率和最佳滑移率的差和误差修正的控制块（见图4）。

图4 模糊逻辑驱动控制框图

块的输出对应着油门是一个0到1之间的数值，摩托车驱动公式（见图2），即此时模糊控制块输出为0；当模糊控制块的输出为1时，摩托车油门全为0；因此，该控制系统依靠节流实现加速或者减速。

建议的控制系统，其输入参数如下公式所示，s是估计滑移率，s_opt是最佳滑移率。

方程（13）确定了最佳滑移率、道路类型和估计滑移率之间的误差。误差用于判断系统是否处于稳定区域，以及最优的控制距离。方程（14）定义了误差的偏移，即在过去的一个瞬间的误差和现在的误差之间的差值。误差偏移变量指出该系统为动态系统。误差范围[-1,1],滑移率在[0,1]之间变化，因此，误差偏移将在[-2,2]。事实上，如果考虑到最佳滑移率小于0.2（见图1），误差范围是[-1,0.2]。误差偏移的范围将会减小，根据经验，应为[-0.4,0.4]。该系统输出为0到1之间，不需要驱动时为0（0% 减小油门，即摩托车继续加大油门），最大驱动时为1（100%减小油门，即关闭油门）。

一旦输入和输出变量被定义，我们必须考虑到牵引力控制系统不需要一直运行。牵引力控制系统只有在前、后轮速度差值大于预定值时才能驱动。

三．经验控制

在本节中，我们描述了一种用于牵引力控制系统，根据经验调节的模糊逻辑控制器。基于专家控制的隶属函数，表现了在滑移过程中驱动产生的变化。参数所建立的隶属函数如图5所示。正如我们观察到的，隶属函数是三角形和梯形。每一个变量的值都反映在表Ⅰ中。

图5 基于经验的隶属函数（a）误差输入（b）误差偏差输入（c）驱动输出

表Ⅰ 隶属函数值（a）误差值（b）误差偏差值（c）驱动值

在我们推出的系统中，规定只有一个运算符，这是[22]中的定义，并且质心法已被用于模糊化阶段，参见[22],[23]。

应指出的是，隶属函数中误差变量并不是关于Y轴对称。正是由于这样的事实，最佳滑移率不能超过0.05-0.2；因此，根据（13），最佳滑移率（s_opt）和滑移率之间的差值s(t)只能在-0.2-0.85之间变化。因此，负值的误差将高于正值的误差。然而，隶属函数中的差分偏移函数是对称的，因为它的变化范围是对称的。最后，由于我们使用了质心法，可以观察到驱动为0时隶属函数能够取得小于0的值。因此，存在一个重心为0，输出为0的输入组合。在驱动最大时情况类似。

一旦输入输出变

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[147893]，资料为PDF文档或Word文档，PDF文档可免费转换为Word