英语原文共 10 页，剩余内容已隐藏，支付完成后下载完整资料

---

汽车车身部件侧向碰撞的优化

摘要

本文探讨了结构优化方法应用到汽车侧面碰撞。局部和全局近似方法的使用进行了比较，得出在一个建议，全局近似方法应用于这种瞬态负载问题。数值模拟已经进行了使用显式有限元程序LS-DYNA研究的问题是B柱的重量最小化，位于汽车的前部和后部的门之间，不会影响车内乘员的安全。所有的结果都在SAAB 95 的B柱。利用线性和二次响应曲面的全局近似的结果表明，B柱的重量可减轻25%而没有安全性的降低。

关键词：优化 响应面 有限元模拟 碰撞 B柱

1 介绍

由于对安全的法律和市场需求的增加，传统车身的重量在未来很可能会增加。同时，环境需求会越来越大，车的重量对于环境将是一个重要组成部分。在欧盟国家里，汽车制造商已经同意整体增加25%燃料效率，由2005和1990相比。这些要求是相互矛盾的，但有了基本的两种手段来满足他们：

1. 新材料的使用，重量轻但强度高和硬度大

2. 结构优化，即采用结构尽可能有效

本文将处理第二个问题。

对于线性分析，结构优化方法已经使用了相当长的一段时间，但碰撞载荷模拟试验和错误一直是唯一的替代性。因此，这个项目的目的结构优化的方法，可以用来分析结构受冲击的特点。这种优化方法的应用将减少B柱的重量，结构部件位于汽车的前部和后部之间的门，没有人损失的安全。

优化方法必须是有效和可靠的，因为碰撞模拟是非常耗时和，并没有导致一个更好的结果一系列的模拟是很昂贵的。

为了获得一个好的工程尺寸大小，用SAAB 95 B-pillar 来当试验样品，B柱是非常重要的一个试验品。

如今，SAAB 95 B柱包括以下几个重要组成部分：

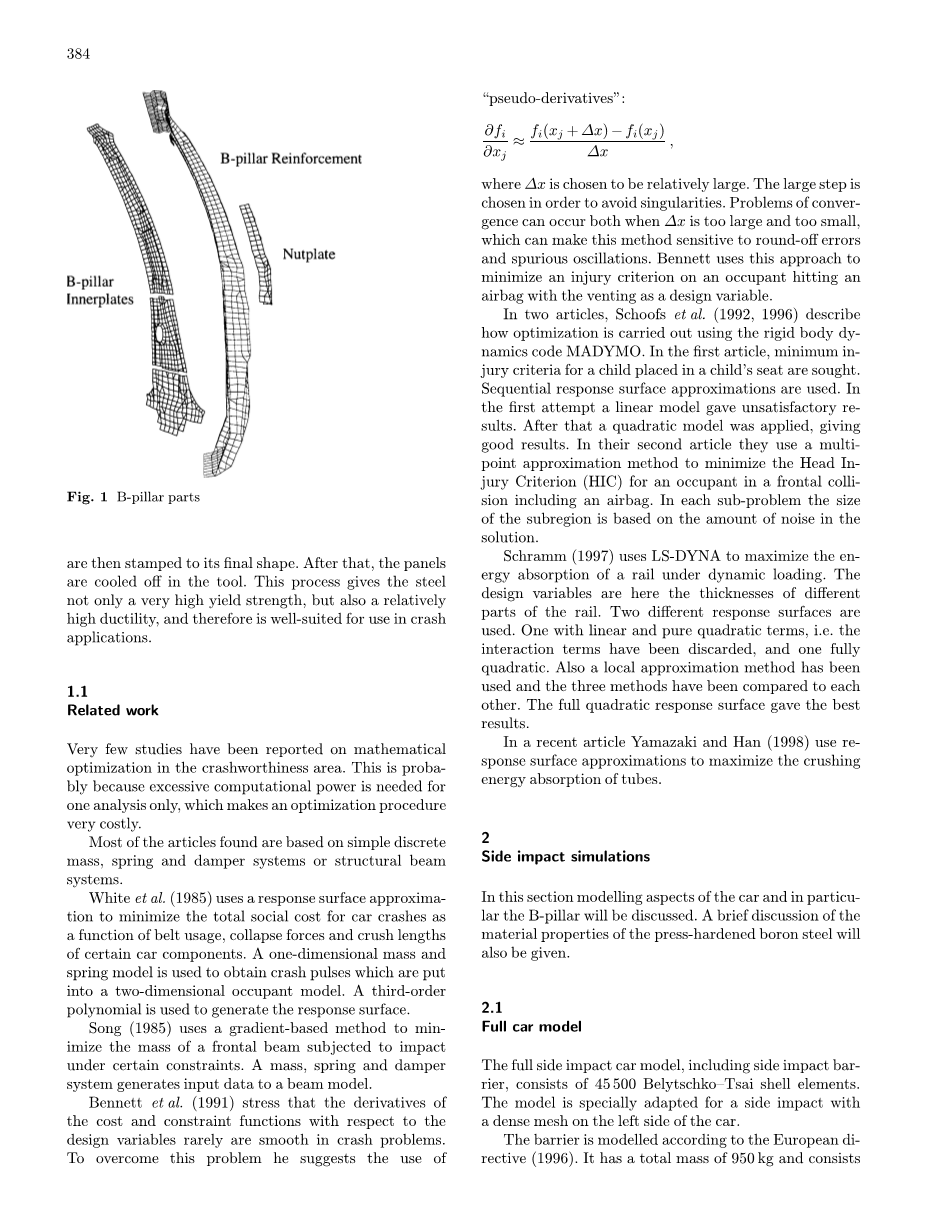
- B柱加强件，

- 三个内板，

- 螺母板，

- 外侧板。

所有这些部件，除了侧面板，如图1所示。

第一个要求是取下螺母板，因为它既重又难组装成柱。但螺母板是重要的耐撞性，因为它降低了B柱上部的入侵速度。所以拆下时，不得有任何安全损失。

为了实现这一目标，决定使用压硬化高强钢做柱子。

因此，硬化高强钢适用于复杂汽车的成形身体的一部分。预制钢板加热到900 摄氏度，然后◦加盖其最终形状。然后，面板在工具中冷却下来。这一过程使钢不仅具有很高的屈服强度，而且高延展性，因此非常适合在碰撞中使用应用.

1.1 相关工作

很少有研究报道的数学优化的耐撞性领域。这可能是因为过多的计算能力配置，只有一个分析的需要，使得优化过程十分昂贵。

大部分的文章是基于简单的离散质量，弹簧和阻尼器系统或结构梁系统。

White（1985）采用响应面法对降低社会总成本为车祸一带的使用功能，撞击力和某些汽车零部件粉碎长度。一个一维的质量和弹簧模型被用来获得碰撞脉冲被放置到一个二维的乘员模型。一个三阶多项式被用来生成响应面。

Song（1985）采用基于梯度的方法最小化的正面梁在一定的约束条件下。质量、弹簧和阻尼器系统将输入数据生成梁模型。

Bannet（1991）强调在设计问题中，关于设计变量的成本和约束函数的导数很少是平滑的。为了克服这个问题，他建议使用∆X的比较大的。这样可以以避免奇点。问题的收敛性可以发生在∆X太大、太小，可以使这种方法对舍入误差和振荡而敏感。。Bannet使用这种方法，以尽量减少受伤标准的乘员撞击安全气囊作为设计变量。

Schoofs et al.在两篇文章。（1992，1996）描述了如何优化采用刚体动态代码MADYMO。在第一篇文章，孩子放在孩子的座位上最小伤害的寻求。序列响应面近似在其中应用。在线性模型给出了不很满意的结果。之后，二次模型的应用，取得了良好的效果。在他们的文章中使用多点近似的方法来减少头部在上海标准（HIC）在正面碰撞乘员安全气囊的结论。在每个子问题的子区域的大小取决于解决方案的噪点。

Schramm （1997）使用LS-DYNA最大限度地在动载作用下轨道能量吸收。设计变量是不同部位轨道的厚度。用两个不同响应面。一个与线性和纯二次项，即交叉变量被去掉，和一个完全二次。此外，已使用的局部近似方法和三种方法进行了比较。完整二次响应面有最好的结果。

近期，Yamazaki and Han (1998) 使用响应面吸收管吸收撞击能力最大化。

2 车身侧面撞击实验模拟

在这部分模拟汽车模型尤其是B柱将着重讨论。还简要介绍了冲压硬化硼钢的材料性能。

2.1 全车模型

全侧面碰撞的汽车模型，包括侧面碰撞的障碍，包括45个500–Belytschko Tsai壳单元。该模型是专门为一个侧面碰撞密集的网格左侧的汽车。

障碍是根据欧洲指令（1996）。它有一个总质量950公斤，由2040个实体单元采用金属蜂窝材料模型可在LS-DYNA里。。为了减少元素变得扭曲的风险，没有硬度和质量的壳单元（空壳）覆盖的固体元素。Malkusson和卡尔森（1998）表明，速度在B柱内的大小涉及粘性的标准，这是一种广泛使用的毁坏一侧面碰撞试验模型。因此，三个速度，如图所示，选择作为我们的限制条件，如图3所示。图3还显示了如何在碰撞过程中B柱的动作，这是模拟在60毫秒以上。

2.2 组成部分模型

在结构优化中，需要大量的功能性评价，即碰撞模拟。如果将使用全车模型，优化过程将是非常耗时的。因此，以减少元件数量的组件模型更高效，但它需要证明的结果也关系到整车模型。创建的模型由B柱加强管理与外侧板和钢筋的内板。总共有4800个壳元素。为了尽可能接近一个完整的汽车碰撞，某些边界条件被加入，如图4所示。这些边界条件是从完整的汽车碰撞模拟，在截面的位移和速度，在大量节省时间事件。因此，我们假设在这些横截面的位移和速度是独立的组件模型。获得一个相对比较（优化），可以接受的误差。

当一些部件被移除时，也引入了一个错误。其中，一些是重要的侧面碰撞保护，例如门和侧撞梁内的门。图5显示了一个相对比较底部的参考点之间的速度是。可以看出，如我们所预期的部分模型最大速度略高于全车模型。我们也注意到，速度曲线最初是陡峭的组件模型，从B柱是目前唯一的抗力构件。B柱加强件进行参数化设计参数与11用预处理LS-INGRID，看到霍尔奎斯特（1998）。五个参数指定在不同截面的柱加强件的宽度，如图6所示，相对于原来的加固。后面五个参数指定高度同一横截面和一个金属片的厚度。从原来的模型选择横截面的位置。交叉面之间的表面线性插值，以便建模过程简单。在过渡区的表面法线不连续造成的压力和浓度。然而，引入的误差小，考虑到所有其他的简化部分。使用的部分之间的线性插值也有影响，等这没有考虑所有的要求，如门铰链的位置。

设计参数可以改高度，如图7被称为设计参数2，可消除折痕由最大为20毫米，宽度相对于设计参数1，可能会减少每边10毫米。设计参数的选择，使角度，alpha;和beta;，在原来的模型是相同的。限制已被设计变量的数目保持低，为以后将讨论的原因。

2.2.1 压硬化硼钢

预制硼钢板先热冲压，随后在刀具冷却。此过程消除厚度变化和残余应力。这些特性连同高屈服强度和相对较高的破坏应变使适用于复杂的汽车结构部件的硼钢。

一个分段线性各向同性硬化材料模型与表1中所示的材料特性，在模拟中使用。

3 防撞性能的局部优化法与全局优化法比较

本节将基于在防撞性能问题上的应用，对局部优化法和全局优化法进行评估。

汽车B柱的简化模型产生并受制于冲击负载。活动期间测量了内车道上三个不同点的速度，所测的速度最大值是我们的约束条件。

被使用的局部优化法为移动渐近线法（MMA），Svanberg（1987）.至于响应面法（RSM），采用Matlab（1998）生成设计，拟合曲面和逼近最优化问题的求解。

3.1 问题描述

MMR和RSM都是在B柱的简化模型上进行测试。模型的尺寸如图8所示。

B柱结构被分为三个线性不同的部位。每个部位都有不同的厚度，由设计参数d1和d3所控制。中立柱的高度会由参数d4改为d7，但是宽度维持80mm恒定不变。

我们想通过以下优化问题来对结构的质量进行最小化：

最小化质量取决于v1max le;3.5m/s, v2max le;5m/s, v3max le;3m/s, 1mmle;d1 ,d2 ,d3 le;4mm, 50mmle;d4,d5,d6,d7 le;200mm.

B柱结构以J2弹塑性，线性等向刚性的材料模型化，并且具有下述材料性质：

• 杨氏模量，E=206Gpa，
• 泊松比，?=0.3，
• 屈服强度，?y=200MPa，
• 等向切线刚性模量 Et=630MPa。

整体反应时间设为30ms，并且期间所给的三个不同点的速度每0.1ms测一次。由于所测速度的信号噪声大，因此经过100Hz的低通滤波器过滤，然后才能取得最大值。

3.2 结果

接下来呈现分别使用MMA和RSM的优化结果。

3.2.1 移动渐近线法（MMA）

MMA是一种线性连续近似法。它由以下基本步骤组成：

1. 选择起始点 d(0), k = 0。
2. 从所给的迭代点d(k)来计算成本c(d(k))，约束条件gi（d(k)）和倾斜度nabla;c（d(k)）nabla;gi（d(k)），i=1，2,hellip;, n，其中n是设计参数的系数
3. 通过以基于上一步的计算值的显性函数代替显性函数c和gi来生成局部的近似子问题
4. 求解近似问题并且将这个子问题的优化解作为下一个迭代点d(k 1)
5. 收敛检查。如果无法取得收敛值，返回第二步。

因为分析灵敏度不明，唯一的解决办法是采用数值差分。这里使用了一个前向差分近似：

nabla;c(dj)= part;c asymp;c(dj h)minus;c(dj).

不同的长度参数h按照顺序被测试，以得到收敛解。长度h被发现不能太短，因为设计参数的极小改变我们都能得到约束条件的巨大变化。图10呈现了随着中间部位的厚度变化时的质量和三个速度。如预期一样，质量随着厚度的增加而线性增加，但是速度的改变为非线性。特别当厚度大概是2.2mm时，我们发现由于翘曲图形的缘故，速度改变十分显著。在设计范围内的其他店也有这种情况，因此数值差分较差地近似了灵敏度。像之前提及的一样，差分近似法需要很宽的步长。

对于这个问题，设计范围7%的差异长度被证明可以收敛，但是必须牢记的是，步长值h是问题相关的。

这个优化的起始点是d1 = d2 = d3 =2mm以及d3 =d4 =d5 =d6 =100mm。每次迭代，都会产生n 1个模拟值用来求解数值差分。每个设计变量都有一个当下的设计点解和被扰时的解。优化结果如表2，3所示。不同起始点对优化结果的影响没有被研究。

3.2.2 响应面法（RSM）

应用全局面法，我们不是从单个点出发，而是从一个面出发。通过这个面，我们想在设计空间内为成本和约束条件拟合曲面。这些表面分别被标记为：

gsurf = Xibeta;i , i = 1,2,... ,p

p是表面的总个数，X包含了表面的多项式。系数因子?通过以下步骤求得。

1. 用D-最优性准则找到一系列起始点，参考Myers and Montgomery (1995)，比如从一个已知设计点数目的用户找到最大化【det XT X】的值
2. 在上一步选择的设计点里计算成本和约束条件 

3. 在设计空间内用最小平方近似来拟合成本和约束条件
4. 在退化问题里用微分法找到最适宜条件
5. 这个结果够好吗？如果不够，增加表面顺序并且（或者）减少兴趣涉及区域并且回到第一步

这里的兴趣设计区域被选为整体设计范围，如（1）中所定义的。在使用七个设计参数时，来拟合线性表面所需要的最小的求解数目是八。对于一个没有相互作用项的纯二次曲面，这个数字是15，对于完全二次曲面，这个数字是36. 在使用这个最小数目的时候，我们可以预料存在很大的误差，因此使用更多的点是有益的，在要求最小数值时。Stander（1999）暗示，50%及以上，这个最小数值将被使用。

通过D-最优性准则，12个设计组从27种可能性中被挑出。每个设计诅都有一个模拟。质量和最大速度都被求解。为了被得到的成本和约束条件，曲面被拟合，并且一个近似最优条件通过微分最优法得到。这个最优点接着通过在最优点上运行模拟。

从表4可以很明显看出，测试模拟与近似模拟有很大不同，这意味着线性曲面对于约束条件并不够好。然而，线性解能给我们在最优化的位置方面一点提示。

现在设计空间被削减在所得的近似最优值附近。每个设计变量被减少为最初范围的一半。这次24个组都被选择，而且纯的二次曲面都与成本和约束条件拟合。从这些表面中，一个近似的最优条件被发现。如前面的步骤一样，为了验证近似最优条件，一个模拟测试在这个近似最优条件下被运行。

这次我们看到测试结果非常接近近似最优条件。这意味着近似比较可取，并且我们总结：一个近似最优条件被发现了。不进一步研究精确最优条件的原因纯粹是经济。碰撞性能模拟非常耗时间因此很花钱。当满足我们预期的结果被得到时，我们就没有投入更多的精力去修饰它。

比较RSM和MMA的最优点，我们发现，两个不同的最优条件被得到了。因为这时一个非凸问

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[138379]，资料为PDF文档或Word文档，PDF文档可免费转换为Word