英语原文共 9 页，剩余内容已隐藏，支付完成后下载完整资料

---

周期三蕴含混沌

Tien-Yien Li；James A.Yorke

1.引言

现象或过程在时间上的演化或变化的方式通常用微分方程或差分方程来描述。最简单的数学情况之一是，当这种现象可以用一个数字来描述时，例如，当一个学年开始时易受某种疾病影响的儿童的数量可以纯粹地作为上一年数字的函数来估计时。也就是说，当年（或时段）开始时的数字可以写入时

=（） (1.1)

其中，将区间映射为自身。当然，这种逐年发展的疾病模型将非常简单，只包含更复杂现象的影子。对于其他现象，该模型可能更精确。如[8，11]所述，该方程已成功用于模拟油井钻井用旋转钻头的冲击点分布，知道这种分布有助于预测钻头的不均匀磨损。例如，如果一个昆虫种群有离散的世代，代的大小将是的函数。一个合理的模型就是一个广义的逻辑方程。

(1.2)

Utida在[10]中讨论了昆虫种群的相关模型。其他的可以见Oster等人[14,15]

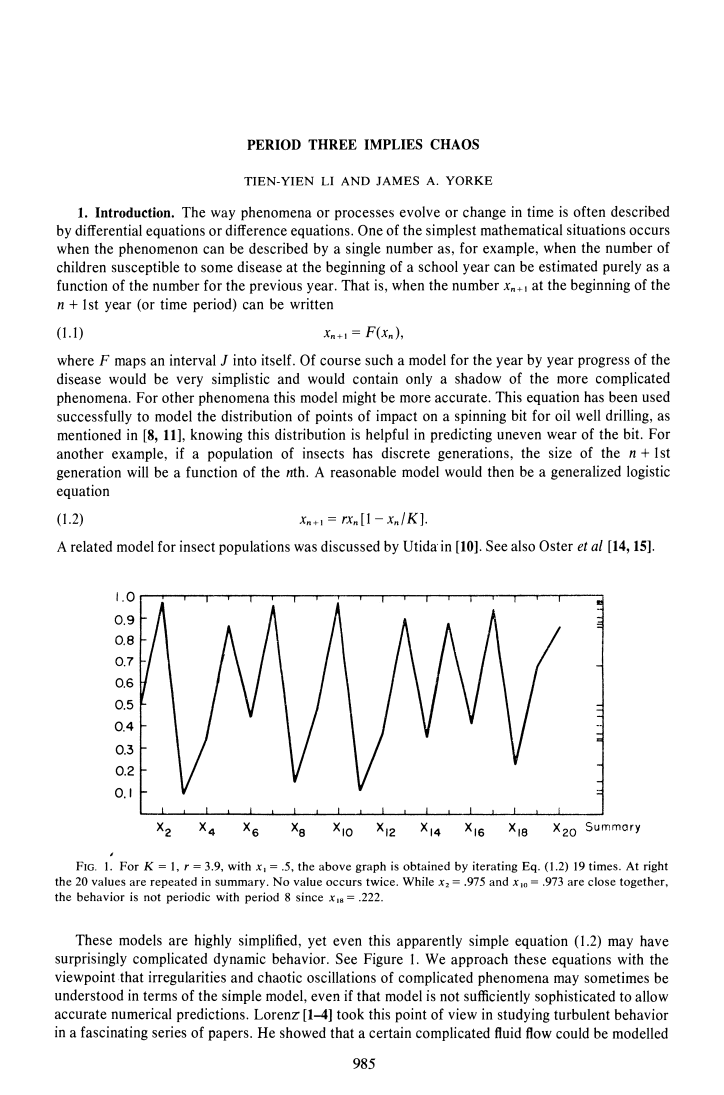
图1

对于=l，= 3.9，且=.5，通过迭代式（1.2）迭代19次得到上图。在右侧有20个值在摘要中重复，没有值出现两次。当=0.975和=0.973紧密相连时，该行为不是周期性的，周期为8，因为.=0.222。

这些模型是高度简化的，但即使是这个看似简单的方程（1.2）也可能具有令人惊讶的复杂动态行为，见图1。我们以这样的观点来处理这些方程，即复杂现象的不规则和混沌振荡有时可以用简单模型来理解，即使该模型不够复杂，无法进行精确的数值预测。Lorenz[1-4]在一系列论文中，从这个角度来研究湍流行为。他表明，可以模拟出某种复杂的流体流动。通过这样的序列，（），（）...保留了原始流的一些混乱的方面。见图2。在本文中，我们分析了序列{()}是非周期的，可能被称为“混乱”的情况。定理I表明，（1.1.）的混乱行为将导致任何一种情况，在这种情况下，大小为的“种群”可以连续两代或更多代地增长，然后达到不可持续的高度，随后就会出现种群崩溃到级或以下。

图2

Lorebz[1]研究了旋转充水容器的方程，该容器绕其垂直轴呈圆形对称。容器在边缘附近加热，在中心附近冷却。当血管呈环形且旋转速率高时，波会不规则地发展和改变形状。从数值求解的简化方程组出发，Lorenz让本质上是连续波的最大动能。作图针对，并将各点连接起来，得到上述图。

在第3部分中，我们给出了一个众所周知的简单条件，它保证周期点是稳定的，然后在第4部分中，我们引用了一个适用于与图2中的结果。这意味着存在一个间隔，因此对于几乎每，序列{（）}的极限点集为。

其实还有许多问题仍未得到解答。例如，周期点的闭合是一个区间，还是至少是一个区间的有限联合？后面会提到其他问题。

额外增加一个证据。May最近在他关于行为作为一个参数是如何变化的独立研究中发现了这些映射的其他强大特性。

2.主要定理

设:。对于，表示，（x）表示()中=0，l，....如果，且表示，我们将说是周期点。如果是周期性的，我们说是周期点；如果是周期性的，我们说最终是周期性的，如果对于某个正整数，是周期性的。因为不需要一对一，所以可能有点最终是周期性的，但不是周期性的。我们的目标是了解点的迭代非常不规则的情况。我们主要结果的一个特殊情况是，如果有一个周期点有周期3，那么对于每个整数.有一个周期点有周期。此外，在中有一个不可数的点子集，它甚至不是“渐近周期”。

定理1.设为区间且:为连续。假设有一个点，对于该点，和，满足

其中

T1：对于每=1,2，bull;bull;bull;在中有一个周期点具有周期。

此外，

T2：有一个不可数集(不含周期点），满足以下条件：

（A）对于每一个，

（2.1）

（2.2）

（B）对于每个和周期点

注：注意，如果有一个周期点，周期为3，那么这个定理的假设是满足条件的。

满足该定理假设的函数的一个例子是如（1.2）中的（3.84，4），和，= ，。有关[0，4]函数迭代的详细说明，请参见[2]。案例在[6，7，12]中讨论。

虽然周期3点的存在意味着周期5中的某一点的存在，但相反的是错误的。（见附录1）。

我们说是渐近周期性的，如果有一个周期点

(2.3)

由（B）可知，集合不包含渐近周期点。我们注意到，不知道方程（1.2）的点不是渐近周期的的中值是什么。

证明定理l。T1的证明介绍了Tl和T2的主要思想。现在，我们用必要的引理给出了T1的结果，并将T 2的冗长证明发布到附录2中。

引理0.设是连续的，其中是一个区间。对于任何紧区间，都有一个紧区间，使得

证明：设，其中。如果，设为[，]的最后一个点，其中，设为后的第一个点，其中。然后。当

引理1.让是连续的，让是一个紧凑的区间序列，所有个区间的和。然后有一个紧凑间隔序列，这样和，对于，对于任何，我们都有。

证明：定义。则。如果被定义为，那么在（由引理0)应用于时，有一个紧凑的区间，这样。这就完成了归纳。

研究某些集合序列如何相互映射或相互映射的技术常被用于研究动力学系统。例如，Smale在他著名的“horseshoe example”中使用了这种方法，在这个例子中，他展示了平面上的同态如何具有无穷多的周期点[13]。

引理2.假设是连续的。让是一个紧凑的区间。假设。还有一个点，比如。

证明：设。在I中选择，使跟随和，因此连续性意味着对于I中的一些必须是0。

假设如定理所示。案例的证明是相似的，因此省略了。写和。

T1的证明：设为正整数。对于gt;1，设为和的区间的序列，并将定义为周期性的，对于如果=l，对于所有，设。

让是证明引理l的集合，然后注意到和，因此由引理2，在中有一个不动点。显然，在的周期不能小于；否则我们需要，与相反。该点是的周期点。

3.周期点附近的行为

对于某些函数，通过对周期点的研究，可以简单地理解点迭代的渐近行为。为了

(3.1)

关于第一阶段和第二阶段的观点的详细讨论可以在[1]中找到，关于的内容，现在我们总结一下其中的一些结果。对于，。

对于，是周期1的唯一点；事实上，对于，序列

对于，周期l有两个点，即0和，

对于gt;3，周期2也有两个点，我们称之为和，当然，和。对于和，收敛到或，而收敛到另一个，除了有的等于周期l的点。只有通过研究周期点，可以理解的行为的可数点。

对于，周期4有4个点，对于略大于的点，倾向于这4个点中的一个，除非对于某些，等于周期1或2的点中的一个。因此，我们可以通过说中的每一点都是渐近周期性的来说明这种情况。

对于每个点都是渐近周期的的值，只研究周期点及其“稳定性质”就足够了。对于具有周期的点的任何函数，如果对于某个区间，我们有

如果在点上是可微的，那么有一个简单的条件可以保证这种行为，即

按链式法则

其中，是第次迭代，。因此y是渐近稳定的，如果

当然，这个条件不能保证不开始的点的极限行为。“接近”周期点或其迭代之一。图2中的函数是由Lorenz有相反的行为，也就是说，在存在导数的地方，我们有

对于这样的函数，每个周期点都是“不稳定的”，因为对于周期的周期点附近的，次迭代比远。要看到这个

逼近。因此，对于靠近的，约为（3.2）的大于1。因此，比远。

我们不知道（3.1）中具有非渐近周期点的的值何时开始出现。对于=3.627，的周期点（渐近稳定）为周期6（约x=0.498）。因此，对于，是周期3的点，因此定理1可以应用于。因为的点不是渐近周期的，所以的情况也是如此。

为了将本节中的情况与下一节中讨论的其他可能情况进行对比，我们定义了点的极限集。如果有子序列收敛到，则点是序列的极限点。极限集定义为的极限点集。如果是渐近周期的，那么是周期的某个周期点的集合{}。

4. 的统计性质

定理1建立了点的迭代行为的不规则性。还需要描述序列（是分段连续可微的（如图2中的Lorenz函数）的规则行为，以及

(4.1)

描述这种函数的渐近行为的一种方法是描述，如果可能的话。第二种方法是检查的平均行为。迭代次数的分数在中表示为。极限分数将表示为

当限制存在时。遍历理论是研究一般空间变换的学科，它激发了以下定义。如果极限分数满足 ，我们称g为的密度。

密度研究的技术使用了非基本的测量理论和功能分析技术，因此我们只能总结结果。但它们的价值在于，对于某些，几乎所有的密度都相同。直到最近，除了最简单的函数外，还没有证明这种密度的存在。最近已经证明了以下结果：

定理2,[5].设满足以下条件：

1）是连续的。

2）除了一点，是连续可微的两倍。

3）满足（4.1）。

然后存在一个函数，对于几乎所有的，g是的密度。对于几乎所有的，，这是一个区间。此外，集合是一个区间，几乎所有的

证据利用了[8]中的结果。在[9]中解决了计算求密度的问题。

（3.1）的详细讨论在[16]中给出，描述了当（3.1）中的参数a在3.0和4.0之间变化时，是如何变化的。

一个尚未解决的主要问题是（对于某些好的函数类）稳定周期点的存在是否意味着几乎每个点都是渐近周期。

附录1：

第5阶段并不意味着第3阶段。在本附录中，我们给出了一个例子，其中有一个不动点，即周期5，但没有周期3的不动点。

设，定义为，在每个区间上

假设是线性的。然后

因此，在中没有不动点。同样地，所以这些间隔都不包含的不动点。

另一方面，

因此，必须在[3，4]中有一个不动点。现在我们将证明的不动点是唯一的，也是的不动点。

设为的不动点。然后是如果，那么将在中，这是不可能的，因为不能是不动点。因此和。如果我们会得到，这是不可能的。因此，，都在中。在区间上，是线性定义的，因此。它有一个不动点，很容易看出有一个唯一的不动点，必须是。因此，没有第3阶段的要点。

附录2：

定理1的T2的证明：设为一组序列

或 且

如果 是整数的平方且其中和当然，如果是整数的平方，则和不是，所以（A.2）中的最后一个要求是多余的。对于，让p（，）表示在中的个数，其中。对于每个，选择作为旧序列，这样

设，因为对于每一个 都有，所以是不可数的。对于每个，根据定理1，存在一个点和对于所有都成立。让。那么也是不可数的。对于，让表示在中的数，其中。我们永远不能有，因为最终会有第3个周期，与（A.2）相反。因此，所有的，依此类推。

对于所有，我们声称（A.4）对，有，存在无穷多的，这样和或者相反。

我们可以假设。那么，所以一定有很多，所以和。

由于和是连续的，存在，因此表示所有。如果 和，则（2）表示

因此.如果，那么有

根据权利要求（.4），对于任何，其如下：

因此（2.1）得到了证明。该技术也可用于证明（B）满足要求。

证明2.2:由于，我们可以选择区间，=0，1，2，bull;bull;这样

设和，则和因为。

为了证明（2.2），我们必须更具体地选择序列。除了我们之前对的要求外，我们假设，如果对于每一个和，则对于，对于，其中，它不是整数的平方。，我们假设。

很容易检查这些要求是否符合（A.1）和（A.2），我们仍然可以选择来满足（A.3）。从可以被认为是的的极限，它得出对于任何，存在无穷多的，使得对于每一个和。为了显示（2.2），让由于，对于任何，存在一个有，对于所有的.那么对于任意的都有对于每一个和我们有

当和和都属于。因此，由于此属性有无穷多，

注。这个定理可以通过假设而不假设来推广，我们把这个证明留给读者。当然是非空的，因为它包含点和c，假设和是可以定义的。

参考文献

剩余内容已隐藏，支付完成后下载完整资料

---

资料编号：[19115]，资料为PDF文档或Word文档，PDF文档可免费转换为Word