使用删失加法回归模型的复杂地形上的时空降水气候学外文翻译资料
2022-11-24 15:12:14

英语原文共 12 页,剩余内容已隐藏,支付完成后下载完整资料
国际气候
诠释。 J. Climatol。 37:3264 - 3275(2017)
在线出版2016年11月9日在Wiley Online Library(wileyonlinelibrary.com)DOI:10.1002 / joc.4913
使用删失加法回归模型的复杂地形上的时空降水气候学
乔治·J·迈尔b,雅各布·W·梅斯纳A,B,尼古拉·乌姆劳夫a和阿齐姆·泽莱伊斯a
a奥地利因斯布鲁克大学经济与统计学院统计系
b奥地利因斯布鲁克大学大气与冰冻圈科学研究所
摘要:灵活的时空模型被广泛用于为降水气候学创建可靠和准确的估计。 大多数模型是基于平方根变换的月度或年度平均值,正态分布似乎是合适的。 这种假设在日常时间尺度上变得无效,因为观测值涉及零点观测值的大部分,并且限于非负值。
我们开发了一个新颖的时空模型来估计在复杂的地形上,使用左删失正态分布在日常时间尺度上降水的完整气候分布。 结果表明,新方法能够解决非正态分布和零点观测的大部分问题。 新的气候学以极高的空间和时间分辨率提供了完整的气候分布,与现有方法相比甚至超越现有方法,即使是在任意地点也是如此。
关键词气候学; 沉淀; 复杂的地形; GAMLSS; 审查; 日常决议
2016年4月4日收到; 2016年7月8日修订; 接受2016年9月12日
介绍
准确了解降水气候学对于农业,风险评估,战略项目规划,水资源管理和旅游等广泛的应用具有重要意义。 此外,气候信息经常用作统计降尺度的背景信息,或作为模型验证的基准。 对于配备降水测量仪器的地点,这项任务很简单。 然而,观测网络通常太稀少以至于不能捕获所有的局部效应,而且由于环境条件和维护目的,观测优选位于较低的海拔和接近人口密集的地区。
为了获得关于没有测量的位置的降水量或降水发生的信息,来自不规则间隔的观测网络的信息必须被带到更精细的(规则的)全区域网格低谷插值。 泰森(1911)指出,简单的插值方案,如最近邻居或算术区域平均值不应该用于降水的内插,因为这些方法不能考虑影响降水的局部因素,例如到山脉的距离,地理位置和其他人(Basist等,1994)。 泰森(1911)发明了一个包含地形属性的区域加权均值方案。 虽然这是作为第一个“简单”扩展提出的,但是今天的统计方法仍然有类似的想法。
*通讯作者:R. Stauffer,奥地利因斯布鲁克A-6020,因斯布鲁克大学统计系和大气与冰冻圈科学研究所。 电子邮件:reto.stauffer@uibk.ac.at
近几十年来,已经有几种不同的方法被开发出来,可以分为三大类。 第一类包括“精确插值方案”,包括反距离加权和各种形式的克里格(例如Biau等,1999; Goovaerts,2000)。 例如,反向距离加权通常不适合作为对地形的依赖性。 对克里格而言,有几个扩展存在包括其他协变量或时空克里格(Snep-vangers等,2003; Aryaputera等,2015)。 第二类包括“区域回归模型”,其中对于每个位置,(简单的)回归模型仅从相邻站的子集进行调整。 例子有PRISM(独立斜坡模型中的降水量高程回归; Daly等,1994,1997,2002,2008)和Daymet(Thornton等,1997)。
第三类插值方法由“平滑样条回归模型”组成,这是本文的重点。 广义相加模型(GAMs; Guisan等,2002)是光滑样条模型的一种常见形式,其中响应数量由一组可能的非线性协变量函数描述。 可行的功能可能是海拔效应,代表季节性的循环效应,或者描述空间分布的经纬度二维样条。 样条模型已经用于不同数量的长期气候学,如温度或降水(Boer等,2001; Jarvis和Stuart,2001; Vicente-Serrano等,2003; Guan等,2009 )。
然而,就降水而言,大多数研究只关注月度甚至年度的方法。
copy;2016作者。 由John Wiley&Sons有限公司代表皇家气象学会出版的“国际气候学杂志”(International Journal of Climatology)。 根据知识共享署名许可条款,这是一个开放获取的文章,允许在任何媒介中使用,分发和复制,只要原始作品被正确引用。
(a1)
0.007
0.006
0.005
密度
0.004
0.003
0.002
0.001
0.000
(b1)
0.030
0.025
0.020
密度
0.015
0.010
0.005
0.000
每月总和
0 100 200 300 400 500
降水量(mm月–1)
每日总结
yminus;axis cut at 0.03
0 20 40 60 80 100 120
降水量(mm日–1)
(a2)
(b2)
密度
密度
0.12
0.10
0.08
0.06
0.04
0.02
0.00
0.20
0.15
0.10
0.05
0.00
每月总和
观察到的
正常
0 5 10 15 20
降水量(mm月–1)
每日总结
yminus;axis cut
at 0.20
Observed Normal Censored
minus;5 0 5 10
降水量(mm日–1)
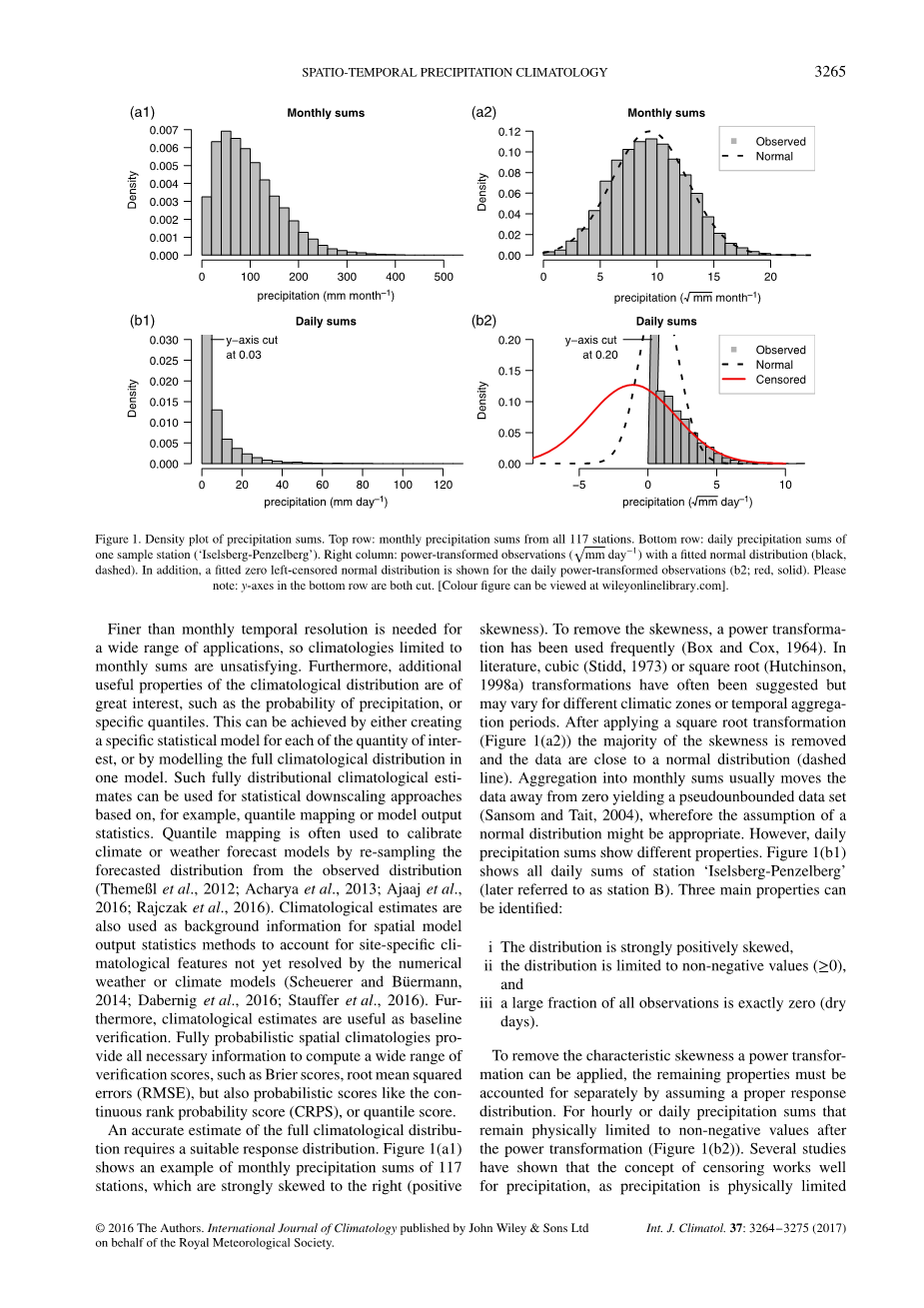
图1.降水总量的密度图 上排:所有117个站点的月降水量。 底行:一个样本站(“Iselsberg-Penzelberg”)的日降水量。 右列:功能转换的观察值(mm日minus;1),拟合的正态分布(黑色,虚线)。 另外,对于每日功率转换的观察值(b2;红色,固体),显示了拟合的零左删失正态分布。 请注意:底行的y轴都被切断。 [颜色图可以在wileyonlinelibrary.com上查看]。
radic;
对于广泛的应用,需要比每月时间分辨率更精细的,所以限制在每月总和的气候条件是不令人满意的。 此外,气候分布的其他有用特性也是非常重要的,例如降水概率或特定分位数。 这可以通过为每个感兴趣的数量创建一个特定的统计模型,或者通过在一个模型中对完整的气候分布建模来实现。 这种完全分布的气候估计可以用于基于例如分位数映射或模型输出统计的统计降尺度方法。 分位数映射通常用于通过对观测分布的预测分布进行重新采样来校准气候或天气预报模型(Themechal等,2012; Ajarya等,2013; Ajaaj等,2016; Rajczak等, 2016)。 气候估计也被用作空间模型输出统计方法的背景信息,以说明数值天气或气候模式尚未解决的特定地点的气候特征(Scheuerer和Buuml;ermann,2014; Dabernig等,2016; Stauffer等, ,2016)。 此外,气候估计值可作为基线验证。 完全概率空间气候学提供了计算各种验证分数的所有必要信息,例如Brier分数,均方根误差(RMSE),以及概率分数(如连续排名概率分数(CRPS)或分位数分数)。
对全面气候分布的精确估计需要合适的响应分布。 图1(a1)显示了117个台站月降水总量的一个例子,这些台站强烈向右倾斜(正向)
偏度)。 为了消除偏态,经常使用权力转换(Box和Cox,1964)。 在文献中,经常提出立方(Stidd,1973)或平方根(Hutchinson,1998a)转换,但是对于不同的气候带或时间聚合周期可能会有所不同。 在应用平方根变换(图1(a2))之后,偏移的大部分被移除并且数据接近于正态分布(虚线)。 汇总到每月总和通常会将数据从零移开,产生一个假定的数据集(Sansom和Tait,2004),因此正态分布的假设可能是合适的。 但是,日降水量显示出不同的特性。 图1(b1)显示了“Iselsberg-Penzelberg”站(以下简称B站)的每日总和。 可以确定三个主要属性:
- 该分布强烈积极倾斜,
ge;
- 分布被限制为非负值(0),并且
- 所有观测值的很大一部分正好是零(干燥的天数)。
为了去除特征偏态,可以应用功率变换,其余特性必须通过假设适当的响应分布来分开考虑。 对于每小时或每天的降水总量,在电力转换后仍然保持非负值(图1(b2))。 一些研究表明,审查的概念适用于降水,因为降水是有限的
到非负值(Messner et al。,2014; Scheuerer,
Phi; (x |
) = {0 (
对于所有:xilt;0
)
2014; Scheuerer和Hamill,2015)。
在这篇文章中,我们提出了一个新颖的时空addi-
cens
i ?, ?, 0
i|?, ?
其他
(3)
这个模型的零点左删失的正常响应,估计了一个日常时间分辨率的复杂地形上降水的全分布气候学。 为了获得这两者,气候平均值和气候 -
Phi; x
当两个数量都设置为低于检查点的零点时,两者分别遵循非审查正态分布的密度Phi;和分布函数Phi;,在检查点(xgt; 0)之上。 在审查
逻辑方差,分布回归模型(Klein
i
点(x = 0),分布f
又是等同的
等,2015)。 分布回归允许所有 i
油膏
将由一组解释性协变量来建模响应分布的参数。 允许分布回归的统计框架通常称为矢量广义相加模型(VGAM; Yee,2015)或位置,尺度和形状的广义相加模型(GAMLSS; Rigby和Stasinopoulos,2005)。 我们使用GAMLSS模型来获得一年中每一天的气候估计以及研究区域内的任意位置的气候估计。 使用功率变换来处理偏度,同时假定零左删失的正态分布处理零下限和数据集中的零观测值的大部分。 这种新的方法允许完全的可扩展性(面积的大小
到正态分布,而密度则表示观测精确到零的概率。 因此,超过零的概率可写为:
y(ygt; 0)= 1 - Phi;(0 , ) (4)
|
最后一个感兴趣的属性是N0的期望。 由于估计值将被拟合到y = z1/p的功率变换尺度y上,所以必须包括这个变换以得到原始尺度(毫米天minus;1)的期望值。 功率转换N0的期望函数可以表示为(附录):
int; ( 1 ) z( minus;1)
infin;
p
1
·
的兴趣,而且空间和时间的分辨率),因此可以很容易地实施和适用于新的
E [z] =
0
z · ?
zp| ,
p dz (5)
数据集或地区。
方法
-
- 左删失的正态分布
模型的响应分布对其整体性能至关重要。 与观测到的每月总和相反,即使在电力转换之后,每日值也显示由大部分零点观测(无降水天数)引起的强烈的零点峰值。 审查的概念是响应本身被限制在一定的阈值 或范围内,在这些限制之外不能被观察到。 假定有一个潜在的不可观察的过程驱动响应,这可以通过合适的协变量来描述。 由于降水量被限制在0毫米以下,因此可以将其视为零( = 0)。 产生的零左删失正态分布如下所示:
y = max(0,ylowast;),ylowast;〜N( , ) (1)
y *表示在正态分布之后的给定参数位置 和尺度the的不可观测的“潜在”响应。 “可观察”的回应y只是潜在回应和审查的最大值。 从这里这个分布将被表示为N0。 N0的密度( CENS)和分布函数(Phi;CENS)可写为:
)
其中z是原始尺度上的可观测响应,
和 是功率转换尺度上N0的估计参数,p代表功率变换的功率参数。
图1(b2)显示了拟合的零左删失正态分布(实线),它能够非常准确地描绘数据的分布。 比较估计的(44%)和观测到的(43%)降水概率,以及估计的(2.3mm天minus;1)和观测到的(2.2mm天minus;1)预期显示,截尾正态分布能够解释大部分零点观测,并能够准确
剩余内容已隐藏,支付完成后下载完整资料
资料编号:[22591],资料为PDF文档或Word文档,PDF文档可免费转换为Word




