纳米润滑膜在近接触界面间粘弹性能的计算模拟研究毕业论文
2020-04-05 10:48:55
摘 要
全氟聚醚(perfluoropolyether,简称PFPE)常用于机械硬盘中以减少硬盘的摩擦与磨损,从而增加硬盘的使用性能和耐久性。随着消费市场对硬盘存储容量需求的日益增加,磁头飞行高度也减小至原子尺度(lt;5 nm)。这就使得磁头与润滑膜有极大可能发生接触,并导致磁头飞行失稳。为了提高机械硬盘工作的稳定性,本文对近接触界面间PFPE润滑膜的粘弹性能进行了分子动力学模拟研究。
本文首先使用Material Studio软件完成了PFPE润滑膜分子链全原子模型的构建。然后利用分子动力学软件LAMMPS模拟了类金刚石(DLC)近接触界面间磁头与PFPE润滑膜的挤压-分离过程,并借助VMD可视化软件对润滑膜微观形态变化进行了观察。与此同时,记录该过程中润滑膜的法向应力,并通过改进的Maxwell力学模型拟合,得到了不同PFPE润滑膜的粘弹系数。
结果表明:在挤压-分离过程中,分子量较小的PFPE受到的法向应力较大,处于较高温度下的PFPE受到的法向压力较大,且从 PFPE压力变化图观察到了应力滞后现象。在300 K温度下,使用Maxwell模型拟合出得到的粘度和弹性模量与实验值存在偏差,经分析后认为是DLC界面采用wall模型,造成了法向应力计算出现误差。为此,重新构建了全原子模型的DLC界面,进行挤压-分离模拟后,得到的粘度和弹性模量与实验值吻合良好,且初始时刻的应力达到弛豫状态。可推知,不同的DLC模型对模拟结果有较大影响。
本文的研究揭示了近接触界面间PFPE润滑膜特殊的粘弹性能,对于改进PFPE润滑膜性能具有重要的指导意义。
关键词:分子动力学;机械硬盘;PFPE润滑膜;法向压力;粘弹性
Abstract
Perfluoropolyether (PFPE) is often used in mechanical hard disks to reduce friction and wear, thus increasing the performance and durability of hard disks. With the increasing demand for hard disk storage capacity in the consumer market, the flying height of magnetic head is reduced to the atomic scale (lt;5 nm). This makes it inevitable for the magnetic head to contact the lubricating film and cause the magnetic head to fly unsteadily. In order to improve the stability of the mechanical hard disk, the viscoelastic properties of the PFPE lubrication film at the near contact interface were studied by molecular dynamics simulation.
In this work, Material Studio software was used to construct the full atomic model of PFPE lubrication film. Then the compression-tension process was simulated by LAMMPS molecular dynamics software package in near-contact interface between the head and PFPE lubricating film. The nanostructures of the lubrication film was visualized by VMD software. At the same time, the normal stress of the lubrication film was recorded in this process, and the viscoelastic coefficient of different PFPE lubrication films was obtained through the improved Maxwell model fitting.
The results showed that in the process of compression-tension, the normal stress of PFPE lubricants increases with the decrease in the molecular weight at higher temperatures. The stress hysteresis was also observed from the normal stress profiles of PFPEs for specific molecular weight and temperature. At 300 K, the viscosity and elastic modulus obtained by fitting the normal stress with improved Maxwell model were substantially deviated from the experimental values. It is probably due to the fact that the DLC wall model provides with a larger attractive interaction and its contribution to normal stress is not considered in LAMMPS. By modeling the DLC with the full atom model, the viscosity and elastic modulus were found to be in good agreement with the experimental values. It is thus inferred that different DLC models can have a great influence on the simulation results.
The study in this work reveals the characteristic viscoelastic properties of PFPE lubrication film at near-contact interface and it is of great significance to improve the performance of PFPE lubrication film.
Key Words:Molecular dynamics; Hard disk drive; PFPE lubricating film; Normal stress; Viscoelastic properties
目 录
第一章 绪论 1
1.1 研究背景 1
1.2 国内外研究现状 2
1.3 研究意义及目的 3
1.4 研究内容 3
第二章 分子动力学方法 4
2.1 基本原理 4
2.2 数值积分 5
2.2.1 Verlet法 5
2.2.2 Leap frog法 6
2.3 系综 6
2.4 时间步长 7
2.5 边界条件 7
2.5.1 周期性边界条件 7
2.5.2 非周期性边界条件 8
2.6 力场 8
2.6.1 力场简介 8
2.6.2 UFF力场 9
2.7 LAMMPS和VMD软件介绍 10
2.7.1 LAMMPS介绍 10
2.7.2 VMD软件 10
第三章 PFPE在近接触界面间粘弹性能研究 11
3.1 分子动力学模型构建 11
3.1.1 PFPE分子模型构建 11
3.1.2 PFPE薄膜模型构建 12
3.2 分子动力学计算参数设定 14
3.2.1 模型平衡 14
3.2.2 挤压分离过程 14
3.3 结果与分析 14
3.3.1 PFPE模型验证 14
3.3.2 PFPE润滑膜粘弹性能研究 15
第四章 总结和展望 23
4.1 总结 23
4.2 展望 23
参考文献 24
致 谢 26
第一章 绪论
1.1 研究背景
由于现代社会的信息高速增长,人们对信息存储、转移的需求与日俱增,基于磁存储技术的机械硬盘应运而生。目前硬盘普遍基于“温彻斯特”(Winchester)技术,采用密封结构,写数据时借助于嵌入到磁头末端的写元件改变磁性介质的极性方向来实现,读数据时则是通过读元件来实现[1]。

图1.1 机械硬盘结构示意图
机械硬盘(Hard Disk Drives,简称HDDs)结构如图1.1所示,主要由磁头、磁盘、主轴等几个部分组成,各组成元件都设计存储在一个密封的腔体中。当机械硬盘工作时,磁盘盘面高速旋转,使得磁头不与盘面发生接触,磁头在悬臂的作用下与盘面保持一定的距离,这个距离称为“飞行高度”(Flying Height,简称FH),这种状态称为“飞行状态”。在这种状态下,磁头既不会与盘面发生磨损,又可以达到读取数据的目的[2]。
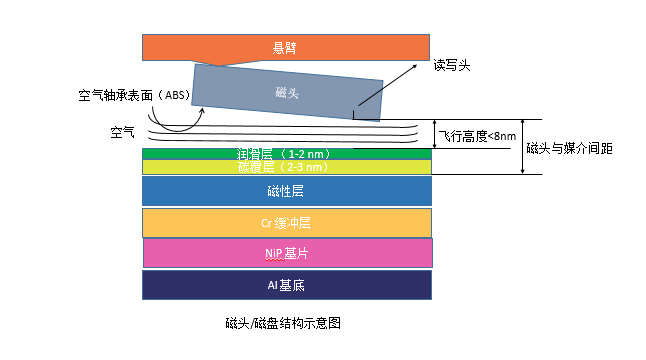
图1.2 磁头-磁盘界面结构示意图
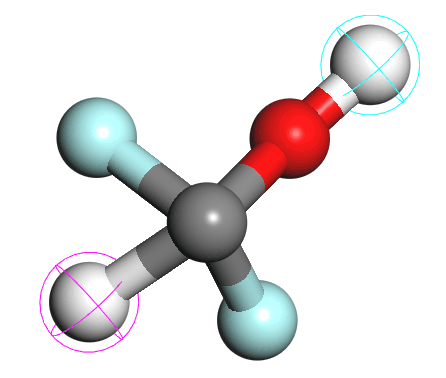
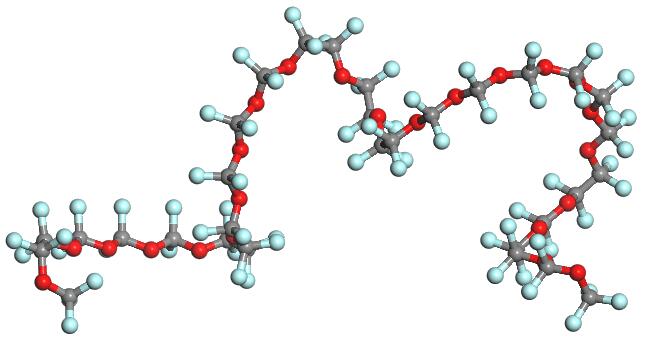
磁头-磁盘界面结构如图1.2所示,主要组成部件为:磁头、润滑膜、磁盘。而磁盘又可分为类金刚石薄膜(Diamond Like Carbon,简称DLC)、磁性层等。为提高机械硬盘的存贮容量和实现磁头磁盘驱动系统更高的记录密度,一种比较便捷的方法是减小磁头磁盘界面间隙,即降低磁头工作时的飞行高度。现在飞行高度普遍降至纳米量级,如8 nm。磁头与磁盘之间并非直接接触,中间存在一层润滑膜以减少磁头磁盘之间的接触。目前,应用比较广泛的商用纳米润滑膜为全氟聚醚。PFPE是一种具有线性主链结构的自由共聚物,化学结构式为:CF3-[(OCF2CF2)p-(OCF2)q]-O-CF3, p/q≈2/3。PFPE主要性能包括较高的热稳定性、氧化稳定性、良好的化学惰性和绝缘性。PFPE还具有低挥发性、较宽的液体温度范围及优异的粘度-温度特性,是一种较为理想的磁盘润滑剂[3]。
1.2 国内外研究现状
李欣等人[4]采用粗粒珠簧模型,应用分子动力学模拟方法,研究磁盘润滑膜极性全氟聚醚在无定型碳表面的结构和铺展特性,表明极性PFPE润滑膜具有复杂的层状结构和复杂台阶状铺展形貌,且两者之间存在一定的对应关系。李欣等人[5]同时也基于粗粒珠簧模型的分子动力学方法考察了非极性和极性全氟聚醚在固体表面的稳定性,发现了润滑膜不稳定是由于极性端基之间的相互作用,极性端基与固体表面的作用对润滑膜的稳定性不大。潘登等人[6]采用改进后的粗粒珠簧模型的分子动力学方法,对磁头磁盘之间润滑剂转移的机理进行研究。实验结果表明增加磁盘表面的润滑膜的厚度会使磁头上润滑剂的体积急剧增加,转移到磁头上的润滑剂的体积随着单个分子中的羟基的数量而显著减少,同时增加单个分子中羟基的数量可改善局部温差对磁头磁盘润滑剂转移的影响,磁头表面的局部高温会使转移到磁头上的润滑剂体积增多。Waltman等人[7]研究了PFPE润滑膜厚度和PFPE分子中羟基的数目对润滑剂转移的影响,发现了PFPE润滑膜厚度减少和PFPE分子中羟基数目增多均会使磁头磁盘间润滑剂的转移量减少。Guo等人[8]采用分子动力学的方法,对磁头磁盘之间的挤压分离过程对PFPE润滑膜的影响进行了研究。计算了挤压分离过程的正压力并发现了由PFPE的不可逆性导致的迟滞现象,并使用Maxwell模型拟合分离过程。
除此之外,学者们还对硬盘所用磁记录介质[9,10]及类金刚石薄膜的结构进行了研究[11]。Zhang等人[12]将脉冲激光电弧沉积法用于制备DLC,并研究了DLC层的物理及摩擦学特性。
1.3 研究意义及目的
机械硬盘在读写数据时,磁头磁盘之间的间隙处于纳米级的范围内。在如此狭小的空间里,磁头与磁盘润滑膜之间的间歇性接触是无法避免的,机械硬盘在移动设备中的使用更是增大了这种接触碰撞的几率。磁头与磁盘的接触碰撞有可能会引起润滑剂向磁头滑块转移,造成润滑膜的损耗,从而降低磁头飞行的稳定性,影响机械硬盘的数据读写性能。为了提高磁头飞行的稳定性,我们需要对PFPE纳米润滑膜在近接触界面间的粘弹性能进行研究,并且探讨不同因素对其性能的影响。本文的模拟结果可以为新型PFPE润滑膜的开发提供一定的数据支持与理论依据。
1.4 研究内容
通过分子动力学模拟方法对PFPE在近接触界面间的粘弹性能进行计算模拟,主要内容有:
- 通过Materials Studio软件构建PFPE的单链模型,然后通过LAMMPS构建PFPE的薄膜模型;
- 基于纳米尺度下的分子动力学方法,对PFPE润滑膜进行平衡计算和挤压分离过程计算,研究PFPE润滑膜向磁头转移的过程;
- 记录挤压分离过程的法向应力变化曲线,并利用改进后的Maxwell力学模型拟合计算流变性能参数,研究不同因素对PFPE润滑膜流变性能的影响。
第二章 分子动力学方法
分子动力学是基于牛顿力学来模拟分子体系的运动的一套分子模拟方法,从不同状态的分子体系形成的系综中抽取样本,进一步计算分子体系的构型积分,从而基于构型积分的结果计算出热力学量和其他宏观性质[13,14]。
分子动力学方法就是通过直接数值解N个分子的运动方程得到这些分子每个时刻的坐标与动量,即相空间中的轨迹,从而用统计方法计算出多体系系统的宏观性质[15]。
2.1 基本原理
设体系有N个粒子,每个粒子的位置为ri,动量为pi (i= 1,2,…N),则(r , p)决定了体系的状态。每个体系微观状态都在相空间中对应一点。
经典牛顿力学说明(r , p)必须满足如下正则Hamilton方程:
(2-1)
其中U(rN)为势能函数,描述体系中各粒子相互作用。
(2-2)
(2-3)
对比(2-2)和(2-3),可得
(2-4)
(2-5)
将式(2-4)和(2-5)代入式(2-2),得
(2-6)
(2-7)
则有
(2-8)
化学行为本质上是一种量子效应或者是一组量子效应,在上述方程中,作为量子效应的化学键全部体现在势能函数U(rN)中。
对粒子i(i= 1,2,…N)来说,有
(2-9)
(2-10)
式(2-9)和(2-10)是一组3N个微分方程,需要用到数值积分方法求解。这样得到每个时刻下的每个粒子的位置和速度,就得到了体系的运动轨迹,从而得知体系特性随时间的变化。
总之,分子动力学是通过一种动态的形式去解决分子体系问题的方法,它依据经典牛顿力学求解粒子的行为,在计算每个瞬时的势能上它依据于量子力学在求算各种体系性质上它依据于统计力学。
2.2 数值积分
有多种方法可以对牛顿运动方程进行数值积分,主要包括2种:Verlet法和Leap frog法。
2.2.1 Verlet法
Verlet法是一种较为简单且常见的方法。
如果借助泰勒级数将粒子的位置展开:
(2-11)
如果将式子中的换成,则上式变为:
(2-12)
将(2-14)和(2-15)两式相加,并略去高次项,得到:
(2-13)
将(2-14)和(2-15)两式相减,则可得到:
(2-14)
即通过和的位置信息可以计算出t时刻的速度。
Verlet法有一个缺点是式中有这一项,由于非常小,因此很容易导致误差[16]。
2.2.2 Leap frog法
Leap frog法是在矫正Verlet法的一个缺点的基础上发展起来的。
(2-15)
(2-16)
对两式分别求导得到:
(2-17)
(2-18)
可得
(2-19)
用替换,可得
(2-20)
又有
(2-21)
得
(2-22)
最后整理的:
(2-23)
(2-24)
知道上一个时刻的位置ri(t),中间时刻和力Fit,就可以用Leap frog法计算出下一个时刻的位置。
2.3 系综
在一定的宏观约束下,各自独立的、处于各种运动状态的、许多结构和性质全部都先沟通的系统的集合称为系综。正则系综、微正则系综、等温等压系综、等压等焓系综是通常使用的4种系综。
正则系综即系统原子数量N、系统体积V、系统温度T保持不变,并总动量也保持不变,又称为NVT系综。正则系综通过蒙特卡罗方法发展来的系综。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: