内置式永磁同步电动机反电动势估算转子位置控制策略研究毕业论文
2020-04-08 14:26:49
摘 要
针对无位置传感器内置式永磁同步电机(IPMSM)的转子位置控制策略,因传统控制策略运算较为复,实现十分困难的缺点;本文采取一种基于定子有效磁链的反电动势模型法来实现永磁同步电机无位置传感器的矢量控制。
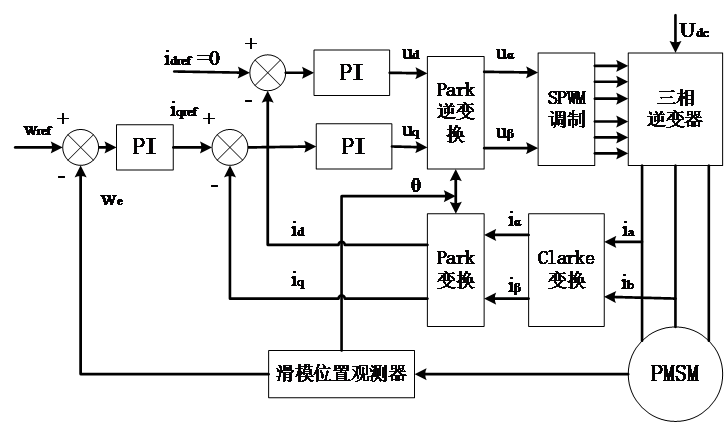
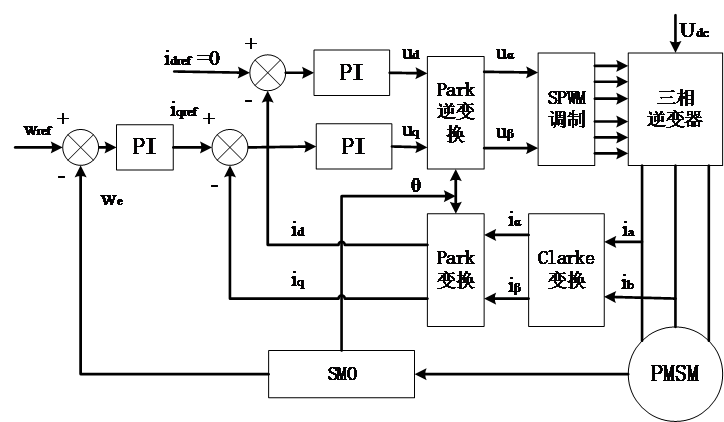
通过比较几种反电动势模型法,其中滑模位置观测器控制的方法,不仅鲁棒性较好,而且易于控制和工程实现,因此使用该控制策略来实现对电动机转子位置和速度的实时观测。而滑模观测器是基于反电动势等效信息实现的,最后利用仿真工具MATLAB中的Simulink仿真平台,构建出PMSM的无传感器矢量控制系统的仿真模型,并进行仿真调试和结果分析,探讨该控制策略的可行性。
最终通过仿真调试和对结果的分析,证明了基于滑模观测器的无传感器矢量控制策略是准确可行的。
关键词:PMSM;反电动势;滑模观测器;矢量控制;Simulink
Abstract
In view of the rotor position control strategy of the interior permanent magnet synchronous machine(IPMSM) without a position sensor technique, the traditional control method is complicated and difficult to implement. This paper adopts a back EMF model based on effective flux linkage to realize control of the interior permanent magnet synchronous machine.
In the back EMF model, a sliding mode observer is used to observe the rotor position and speed of the motor in real time with good robustness, simple control algorithm and easy engineering implementation.Combined with IPMSM's mathematical model and vector control theory, a simulation model of sensorless IPMSM vector control system based on Simulink is established.Then the simulation and result analysis is carried out,and control strategy is feasible.
Finally, the accuracy and feasibility of the sliding mode observer based sensorless vector control strategy are verified through the analysis of the simulation results.
Key Words: PMSM; back EMF;sliding mode observer; vector control; Simulink
目 录
摘要 I
Abstract II
第1章 绪论 1
1.1 研究的目的和意义 1
1.2国内外研究现状 2
1.3研究内容 3
第2章 永磁同步电机的矢量控制 4
2.1永磁同步电机的数学模型 4
2.1.1三相静止坐标系下的数学模型 5
2.1.2坐标变换 5
2.1.3两相静止坐标系下的数学模型 7
2.1.4两相旋转坐标系下的数学模型 7
2.2永磁同步电机矢量控制原理 8
第3章 滑模控制器的设计 10
3.1滑模变结构控制原理 10
3.2 滑模观测器的设计 11
3.2.1永磁同步电机滑模位置观测原理 11
3.2.2 滑模位置观测器参数确定 15
3.3 本章小结 17
第4章 仿真结果分析 19
4.1仿真工具的介绍 19
4.2 系统仿真模型的搭建 19
4.3 仿真结果调试分析 20
4.4 本章小结 22
第5章 总结与展望 24
参考文献 27
致谢 29
附录A 永磁同步电机仿真模型 30
附录B SMO模块仿真模型 31
附录C SVPWM模块仿真模型 32
第1章 绪论
1.1 研究的目的和意义
永磁同步电机不仅体积较小、可靠性好、效率高而且适应性强;随着控制技术的不断发展,它在各种高性能伺服系统中的应用也越来越广泛。在电机的高性能控制系统中,需要对电机进行磁场定向控制。而这一过程的实现是十分困难的,需要从电机转子中获取位置信息。通常情况下会采取使用机械式传感器来检测转子的位置,但是,这样不仅会增加了整个系统的成本,而且会造成系统的可靠性降低。因此,对永磁同步电机的控制技术研究变得越来越多,尤其是无传感器控制技术,它的研究也成为了目前电机控制技术领域的热门[1]。
要实现电机的闭环控制,就要获取相应的控制信号,其中转子的位置和转速信息是至关重要的,它们是作为反馈量实现闭环控制的重要因素;但是使用硬件式传感器会给永磁同步电机带来许多不利因素的影响。而通过获取电机的各种物理量来实现对电机的控制,采用这种控制方法可以实现电机的无传感器控制;目前许多学者对这方面进行了深入的研究。在控制过程中,对PMSM实现高动态性能、高精度的控制,将会大大提高电机的利用效率[2]。以前都是通过采用传统机械式的传感器实现控制的,这样不仅会增加系统的成本,而且可靠性还十分低,这些问题都是十分不利于电机的控制。无速度传感器技术不仅可以省去机械式传感器,而且使系统的控制性能得到大幅度提高,成本也相应的降低。它是结合电机在不同坐标系下的数学模型,通过检测电机的电压和电流信号,从而获取转子的位置和转速等信息,进而实现对电机的控制。
目前,对永磁同步电机的无位置观测器器的控制算法主要包括两种:第一种是建立在电机的数学模型基础上的,通过对基波的方程式进行计算,从而实现控制;第二种方法通过外加注入高频信号,这样就能够在定子侧的绕组上获取得到转子的位置和转速信息,进而实现对电机的控制。对于电机控制技术来说,要想不断发展和完善,提高适用范围,就得降低成本并且提高它的控制性能。而实现无传感器控制技术更是改善电机控制调速性能的基础。因此,不断研究发展无位置观测器控制技术的设计是是有着较大的作用的,它对电机的开发与实际应用有着实际的指导意义。
其中,针对永磁同步电机无速度观测器器较常用的控制方法主要为扩展卡尔曼滤波法、模型参考自适应法、滑模观测器法和高低频注入法等。虽然这些方法也能在一点范围内控制电机,但它们都存在一些模型算法复杂,计算量大,涉及参数较多等问题。反电动势法其物理概念较为清晰,计算量小,而扩展卡尔曼滤波、高频注入法、滑模观测器等观测方法,也都是基于电机反电动势提出来的[3]。
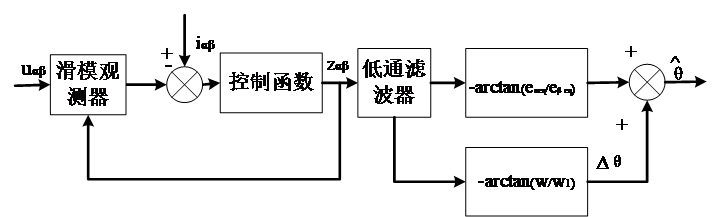
而对于反电动势模型法的控制原理,它通过建立有效定子磁链模型,能够将凸极交流电机转化为非凸极电机的类型,进而可以简化无位置传感器控制系统的分析与设计。经过定子电流滑模位置观测器可以获得等效反电动势信息,并且对该信号作标幺化处理,这样就可以避免位置误差信息受转速变化的影响,从而简化位置观测器的设计难度。
而采用反电势模型法的位置观测器来估算转子位置的矢量控制方法,这类算法无需传感器,通过直接获取电机定子侧的电压和电流,根据它们的磁链关系直接计算转子的位置角度信息。这种控制方法有着较大的优点对滤波器的依赖性小,而且算法易于实现、控制系统简单高效。因此基于反电动势来实现内置式永磁同步电机的矢量控制更是电机控制技术领域的研究热点[4]。
1.2国内外研究现状
随着永磁材料的出现而产生了永磁同步电机,这对电机控制理论的改善产生了巨大的影响。而且对永磁同步电机的设计制造、控制技术及建模分析等多方面都不断进行完善和改进。在技术不断的发展过程中,对永磁同步电机的等效磁链研究也越来越多。而对数学模型不断进行分析计算和仿真研究,这将会使得永磁同步电机得到快速的发展,而且对电机的控制技术也会不断得到发展和完善。
关于最初的电机矢量控制技术,德国西门子公司的工程师 F. Blaschke最先提出了矢量控制理论。而空间矢量控制,它的本质就是对电机的磁场进行定向控制。磁场的定向方式就是由定子磁场、转子磁场以及两者的合成磁场(气隙磁场)这三者所共同确定。因此,异步电机要想具有良好的控制性能,就需要进行相应的控制变换,实现像直流电机一样具有良好的控制性能。具体控制方案就是将定子绕组上的交流量转换为直流量,在此过程中常使用矢量控制策略,对电机的转子磁场进行定向控制。
因为对电机的控制技术发展越来越快,所以对永磁同步电机的无传感器控制策略研究也变得越来越多,国内外学者一直对这方面进行了深入的研究。现今,对永磁同步电机的无传感器矢量控制技术的研究发展现状为:能达到无传感器运行。但该控制技术仍然尚不完善,精度和调速规模仍然不满足要求,应用场景十分有限。目前永磁同步电机的发展的趋势为:不断改进制造技术,而且将会与无传感器控制技术的设计一起进行,从而提高控制性能,达到电机控制技术的最优效果。
国外的研究人员对电机的矢量控制技术也进行了十分深入的研究。1993年, Matthew J.Corley和 R.D.Lorenz教授为了更好地实现对永磁同步电机的矢量控制,取消机械师传感器,改善控制性能,他们提出了使用高频信号注入法来实现控制。而对于使用反电动势观测器的电机控制技术方案,Lorenz教授也发表了相应的论文。随着无传感器控制技术方案的越来越成熟,对电机的各种控制策略及措施韩国Seung-ki Sul教授自1995年起就进行了深入的研究,随后他就发表了多篇相关性的论文。此外,日本的 Kanagawa University,斯洛伐克的Zilina大学,巴西的 Universidade Federal de Campina Grande等高校的研究人员,也都在进行该领域的研究[5]。
而近些年来,国内对于永磁同步电机的控制技术的研究也在逐渐增多,特别是无传感器控制技术。清华大学的李永东教授等人不断对PMSM的控制技术进行研究,随后就发表以一些有关无传感器控制技术的论文。针对其中的高频注入法,沈阳工业大学的王丽梅教授进行了较为深入的研究,将该控制方法不断进行完善。此外,南京航空航天大学、天津大学、浙江大学、西安交通大学、上海交通大学、上海大学等高校都对永磁冋步电机的无传感器控制方法进行了研究[6]。现在,已经有很多国内学者都在国际上发表了英文形式的论文。
1.3研究内容
对电机来说矢量控制技术是高性能的交流控制方式,也是当代交流传动技术发展的方向之一,而对于矢量控制策略来说,使用无位置观测器的控制方法拥有着较多的控制优点,能够提高控制系统的性能,改善传统控制方法的不足,并且它的适用范围也会扩大。所以,该控制策略成为了现今的研究热点。本文结合转子磁场定向的矢量控制策略,在无位置传感器内置式永磁同步电机的矢量控制基础上 ,采用一种基于有效磁链的反电动势模型法来实现永磁同步电机无位置传感器的控制。论文主要研究内容如下所示:
第1章主要介绍本论文的研究目的及意义、永磁同步电机无位置传感器及其矢量控制技术的发展现状,并对本课题的主要研究内容进行了阐述。
第2章详细介绍三相永磁同步电机在各种坐标系下的数学模型以及坐标变换;还阐述了永磁同步电机通过传感器进行矢量控制原理的基本理论。
第3章首先对滑模变结构的控制原理进行了介绍,然后介绍永磁同步电机基于反电动势模型法的滑模控制原理;最后完成了对滑模位置观测器的设计以及各项参数的确定。
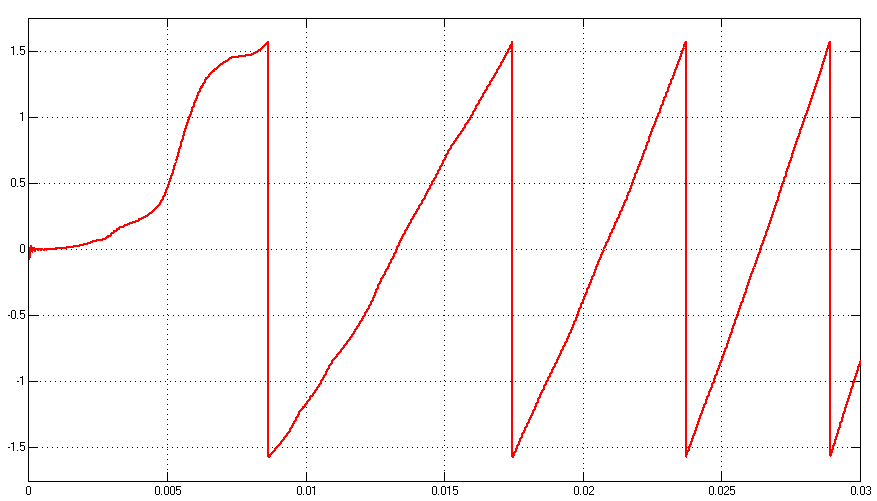
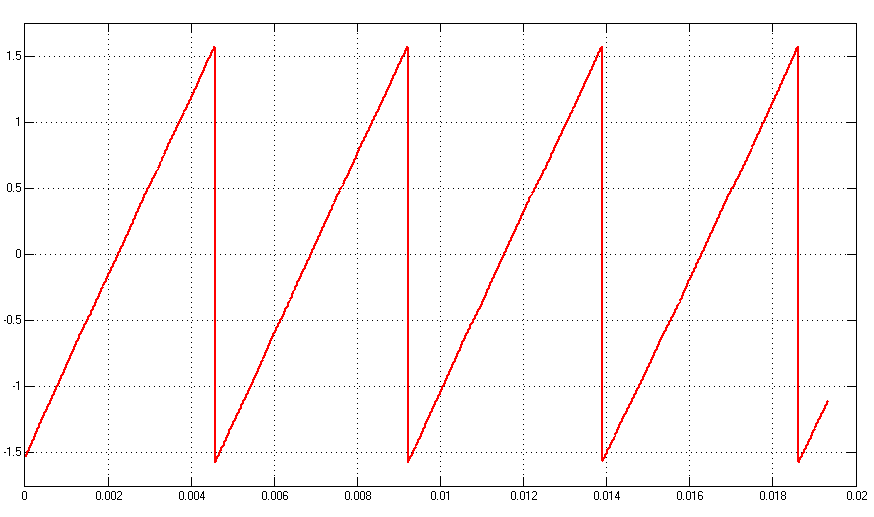
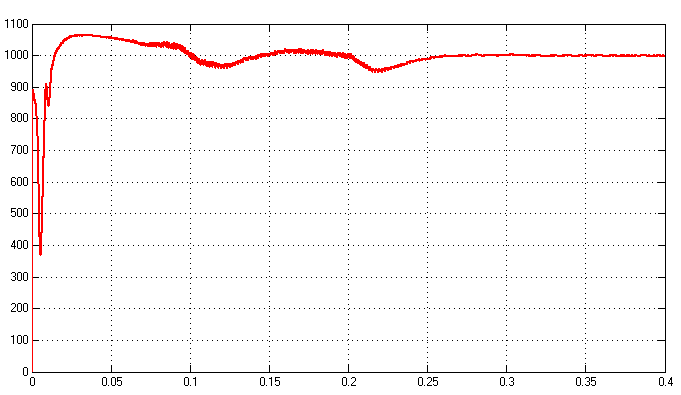
第4章主要主要进行仿真研究,构建永磁同步电机基于滑模观测器控制系统的仿真模型,对仿真结果进行分析。首先,简单介绍仿真环境;然后,完成对系统仿真框图的搭建;最后,对永磁同步电机的转子位置估计算法进行仿真验证并分析结果的准确性和影响因素。
最后,总结了本论文所研究的内容以及完成的工作;针对本文的研究内容中存在的问题及不足之处进行分析并提出优化改进思路。
第2章 永磁同步电机的矢量控制
2.1永磁同步电机的数学模型
对于永磁同步电机来说,它是由三部分组成的,包括:电机外壳、定子以及转子。而永磁体便是安装在转子位置上的,因为安装位置有所不同,永磁同步电机可分为两类,即内置式永磁同步电机(IPMSM)和表贴式永磁同步电机(SPMSM)。永磁同步电机在运行的过程中,定子电感是不断发生变化的,而且是非线性变化。所以该类电机的控制性能较为复杂,受其他的因素影响也较为严重,主要是定子电流换相时候产生相移的影响。
通常情况下,要实现多永磁同步电机的控制较为复杂,它内部结构设计较为复杂,存在非线性和饱和效应的电磁装置。而对于电机的状态方程,就更难进行精确求解,因为它是一个高阶微分方程。所以,在控制过程中,要实现控制,就必须对它进行简化,将它化简称成为一个简单的方程组,即二阶微分方程组。实际过程中,通常会忽略不必要的影响因素,做出下面的假设:
- 忽略谐波效应,定子三相绕组完全对称且互差120度电角度,且产生理想正弦磁动势;
- 忽略永磁体的非线性饱和因数素,设定各相绕组的阻值和电感恒定,且Ra=Rb=Rc=Rs,La=Lb=Lc;
- 不计磁滞损耗和涡流损耗等;
- 不考虑频率和温度等因素的变化对参数的影响;
- 转子上没有阻尼绕组,永磁体没有阻尼作用;

图2.1 永磁同步电机三种坐标系在空间上的矢量图
对PMSM的研究过程中,针对矢量控制算法,时常要用到它的数学模型。而数学模型是建立在不同的坐标系下的,通常要使用到三种坐标系:即三相静止坐标系(abc坐标系);两相静止坐标系(α-β坐标系);两相旋转坐标系(d-q坐标系)。图2.1就表示三种坐标系在空间上的相对位置,下面将根据电机的原始状态方程建立三种坐标系下的数学模型。
2.1.1三相静止坐标系下的数学模型
在三相坐标系即ABC坐标系下电机的电压方程为:
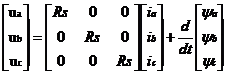 (2.1)
(2.1)
式中:u表示为abc三相的电压;
i表示为abc三相的电流;
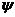 表示为abc三相的磁链,
表示为abc三相的磁链,
Rs为电枢电阻。
磁链方程为:
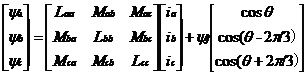 (2.2)
(2.2)
式中:L表示自感,且有Laa=Lbb=Lcc;
M表示互感,且有Mab=Mac=Mba=Mbc=Mca=Mcb;
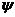 f表示转子永磁磁链,而θ角表示N极与a相轴线夹角。
f表示转子永磁磁链,而θ角表示N极与a相轴线夹角。
式子(2.2)构建出电机的磁链方程式,由表达式可以看出,电机在三相静止abc坐标系下的数学模型是十分复杂的。它是一个多变量复杂系统,要利用它来实现对电机的控制较为复杂,难以在实际中应用。
2.1.2坐标变换
(1)3s/2s变换
对于坐标3s/2s变换也称为Clark变换,简称3/2变换,它是将电机的电压、电流和磁链方程式从三相静止ABC坐标系然后变换到两相静止αβ坐标系下的方程。
在分析实际问题时,将两种坐标系的原点放在一起,通过取α轴与定子A相绕组的中心线相重合,β轴是通过逆时针90度得到的,相应的超前α轴90度电角度。变换过程中始终要保持合成的磁动势相等,所以这两种坐标系下合成的磁动势在α、β轴上的投影应该相等。
根据磁动势表示为匝数和电流两项的乘积,那么在ABC坐标系中设每相绕组的匝数为N3,而在αβ坐标系中设为N2,将得到如下方程式。
 (2.3)
(2.3)
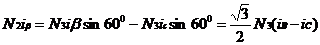 (2.4)
(2.4)
因为变换前后总功率不变的原则,所以匝数比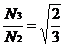 。
。
使用矩阵表示为:
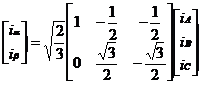 (2.5)
(2.5)
由式(2.5)可以推导出3s/2s变换的矩阵为:
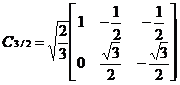 (2.6)
(2.6)
由式子(2.6)便得到了电流的变换矩阵,电压、磁链的变换矩阵也是一样的。而从两相静止坐标系到三相静止坐标系的变换称为2s/3s变换,即Clark逆变换。
(2)2s/2r变换
而坐标2s/2r变换也称为Park变换,即从αβ坐标系变换到dq坐标系。变换的原则是一致的,即合成磁动势相等。
由等效变换原则可知,在坐标的变换过程中合成的磁动势在相应的坐标系下投影是相同的,因此可得到下列方程式:
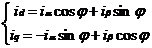 (2.7)
(2.7)
写成矩阵形式为:
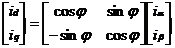 (2.8)
(2.8)
所以可以得到2s/2r的转换矩阵为:
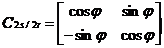 (2.9)
(2.9)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: