台风灾害下电网恢复策略研究毕业论文
2020-04-09 15:35:37
摘 要
Abstract II
第1章 绪论 1
1.1 本文研究的目的与意义 1
1.2 电网恢复的研究现状 1
1.3 本文研究内容 2
第2章 复杂网络社团结构 4
2.1 引言 4
2.2 复杂网络理论的基本概念 4
2.2.1 度与度分布 4
2.2.2 最短路径 5
2.2.3 介数 5
2.2.4 模块度Q 5
2.3 本章小结 6
第3章 电力系统恢复分区的划分 7
3.1 引言 7
3.2 电网恢复分区的划分原则 7
3.3 电力系统的抽象与简化 8
3.4 电网恢复分区划分算法 8
3.4.1 凝聚阶段 8
3.4.2 分裂阶段 9
3.4.3 边介数的计算 9
3.5 电力系统恢复分区的检验 11
3.5.1 模块度Q函数计算 11
3.5.2 电气特性检验 11
3.6 分区内恢复路径的选择 11
3.7 本章小结 12
第4章 算例分析 13
4.1 凝聚阶段 13
4.2 分裂阶段 15
4.3 恢复分区的校验 17
4.4 最短恢复路径的确定 18
4.5 本章小结 19
第5章 结论与展望 20
5.1 研究结论 20
5.2 研究展望 20
致谢 21
参考文献 22
附录MATLAB编程代码 24
附1 边介数的计算编程代码 24
附2 模块度Q值计算的编程代码 26
附3 最短路径编程代码 26
摘要
随着全球变暖,台风等自然灾害频发,给人民生活带来极大的不便,也给全球经济造成严重的损失。台风灾害下电网故障或损毁情况。
本文对电网恢复分区问题,提出了一种新的方法,将复杂网络的社团结构划分理论运用到电网恢复分区的划分问题中。此方法将分区过程分为凝聚与分裂两个子过程。凝聚过程主要处理电力系统黑启动阶段的实际情形对分区的特殊要求,对电网进行一定程度的简化;分裂过程对经凝聚过程简化后的电网采取GN分裂算法确定大停电后电网的恢复分区。通过模块度Q值和电气特性两方面对恢复分区进行校验,判断分区划分的合理性。校验通过后,采用Floyd算法寻找分区内机组间恢复的最短路径。最后以IEEE10机39节点系统为例校验此分区算法和最短恢复路径的合理性和可行性。
关键词:社团结构;恢复分区;GN分裂算法;Floyd算法;最短恢复路径
Abstract
With global warming, frequent natural disasters such as typhoons have brought great inconvenience to people's lives and caused serious losses to the global economy. The fault or damage of the power grid under typhoon disaster.
In this paper, a new method is proposed for the restoration partition of power grid, and the theory of community structure division of complex networks is applied to the partition of power grid recovery partition. This method divides the partition process into two sub processes: agglomeration and splitting. The coagulation process mainly deals with the special requirements of the actual situation of the power system in the black start stage, and simplifies the power grid to a certain extent. The split process determines the recovery partition of the power grid after the large blackout after the GN splitting algorithm after the condensed process is simplified. The rationality of partition partition is judged by two aspects of modularity Q value and electrical characteristics. After passing the calibration, the Floyd algorithm is used to find the shortest path between units in the partition. Finally, take the IEEE10 39 node system as an example to verify the rationality and feasibility of the partition algorithm and the shortest recovery path.
Key words:Community structure; restoration partition; GN splitting algorithm; Floyd algorithm;the shortest recovery path
第1章 绪论
本文研究的目的与意义
随着全球变暖,台风自然灾害频发,给社会,经济和人民生活造成了严重影响和极大损失。例如,台风“云娜”在2004年于浙江登陆期间,据统计,10kV倒杆输电线路有2106条,倾斜杆塔21632基,跳闸的110kV线路有106条,跳闸的35 kV和10 kV配电线路共有2362条,10 kV及以下线路毁坏长度达3878 km[1]。海南电网在2005年台风“达维”登陆期间,部分电厂连续跳机解列,从而导致海南电网全黑[2]。福建省的福鼎县在2006年台风“桑美”登陆期间,沿海90%以上以及内陆50%以上的线路发生倒杆,共有9460根杆塔断裂,损毁了90%以上的10kV及以下的线路[3]。广东电网在2014年超强台风“威马逊”的登陆期间,导致10 kV及以上线路跳闸758条次,10 kV及以上线路的倒杆倒塔数6530基,10kV以下线路的倒杆数12191根,受损线路1986 km,215.6万用户受到影响[4][5]。在国外,2013年登陆的台风“桑迪”对多个国家都造成了严重的影响[6]:在美国,导致美国东部的820万户住户电力中断,超百人遇难,造成550亿美元的经济损失;在古巴,导致11名古巴人丧生,4200多所住房被毁,造成21.21亿美元的经济损失;在海地,50多人遇难,20多人失踪,约2万所房屋受到不同程度损坏,受灾总人数高达180万;在加拿大,约有20万人的电力中断。
现代电网的结构越来越合理,网架也变得越来越坚固,加上继电保护和自动装置在配置和性能等方面的不断优化,总体来说电网能比较可靠的稳定运行,发生大面积停电事故的概率会非常小。但从上述可以看出近年来台风发生的频率及强度均有增强趋势,给电网正常运行带来了严重危害。既然台风灾害下电网故障或损毁不可避免,那么运用适当的防御策略并确定有效的恢复策略能在很大程度上减少停电面积,缩短停电时间,减少因台风灾害导致大面积停电后造成的不便和损失。因此对电网大停电后的恢复过程进行研究意义重大。
1.2 电网恢复的研究现状
恢复力( resilience)的概念最早由美国生态学家 Holling于1973年引入生态学领域[7],定义为系统吸收干扰并继续维持其功能、结构、反馈等不发生质变的能力,随后环境科学、社会学以及工业等领域也逐渐被运用[8][9][10][11][12]。电网恢复是指电网发生大面积停电后,由系统中存在的带电孤岛或其它具有自启动能力机组带动无自启动能力的机组,逐步扩大带电区域,最终实现整个系统正常运行的过程[13][14]。目前,大多将系统恢复过程划分为黑启动阶段、网架重构阶段以及负荷全面恢复阶段三个阶段[15][16][17][18][19]。
在网架重构阶段,恢复方法一般可分为2种:串行恢复和并行恢复。串行恢复是指在大多数发电机并网前就对整个系统进行充电;并行恢复是指先将电网分成几个分区,各个分区同时恢复,然后在所有的分区都恢复完成后,再将各分区同步并列,从而恢复整个电网。由此可见,在大停电后制定的电网恢复方案中,合理的电网恢复分区的划分对缩短整个电网恢复供电的时间具有重要作用。
在恢复分区划分方面,目前的划分电网恢复分区的方法主要可以分为两大类: 固定分区法和动态分区法。
固定分区法是大多以行政区和地方电力公司的管辖范围为基础,一般在大停电事故发生前制定,在实际恢复时能简化地区调度间、地区调度与上级调度间的通信与协调,可以避免在大停电事故发生后紧急状态下的管理混乱[38]。例如,河北省南部电网在黑启动时划分为邯邢区、石家庄区、保定区和衡沧区四个区域[39];南方电网根据其管辖内各省(区)电网的黑启动电源、重要机组及重要变电站的分布情况等,在各省级行政区划的基础上,分别将广东、广西、云南、贵州和海南电网划分为13、7、3、4和2个恢复分区[40];天津电网结合地理位置和黑启动电源分布的情况,制定了3种黑启动分区划分方案[41]。江苏电网在黑启动时将全省划分为南京、常州和镇江、无锡、苏州、扬泰通、徐淮宿盐连等6个分区[42]。山东电网在大停电时也将全网划分成6个分区并行恢复[43]。但是,固态分区法有一个缺点:即此分区方法划分的分区是根据地理位置以及黑启动电源分布状况等因素在大停电前就确定的,因此,此方法的主观性较强,不能在恢复过程中进行实时优化。
动态分区法是以电网停电后实时获取的信息为基础,以恢复时间、负荷恢复量、操作次数、恢复风险等指标为优化目标,采用优化算法寻找最优划分方案,此分区方法可以依据各指标的重要程度有针对性地寻优,根据不同的优化目标给出不同的划分结果[38]。文献[44]以机组启动时间最短为目标函数,采用遗传算法,并综合考虑分区方法和分区内部节点的恢复路径、恢复顺序,优化系统分区。文献[45]将线路长度、电压转换次数、中间电站个数等指标综合考虑,并采用禁忌搜索算法对系统进行划分。然而,动态分区法对停电时获取的电网实时信息过分依赖,因此,若在大停电事故发生后,由于通信中断等原因不能得到足够的实时信息,分区的优化将会受到很大的影响,从而导致分区的划分结果可靠性低,甚至导致分区内部不能进行恢复。
由此可以看出,一个合理的恢复分区的划分方法,应当是结合固定分区与动态分区的优点,尽量避免二者的不足。因此,本文提出了一种新的分区划分方法,本文发现复杂网络的社团结构的特点与电网恢复分区的特点相似,因此将复杂网络的社团结构理论应用到电网恢复分区的划分问题中,此算法将分区过程分为凝聚与分裂两个子过程。
1.3 本文研究内容
本文的主要研究内容是对大停电后的电网进行恢复分区的划分并确定分区内机组的最短恢复路径,从而加快电网恢复供电的速度,缩短负荷的供电恢复时间,从而减少因停电造成的经济损失。 本文主要结构和具体的研究内容如下:
- 是研究的开头,主要阐述了研究的目的和意义,并对目前关于本题的国内外研究现状进行调研,最后给出了本文的主要研究内容。
- 对复杂网络的定义及社团结构的相关概念进行介绍,为第三章电力电网的恢复分区做好基础铺垫。
- 对电网恢复分区问题,提出了一种基于复杂网络社团结构理论的电网恢复分区划分算法,此算法将分区过程分为凝聚与分裂两个子过程。凝聚过程主要是对电网黑启动阶段进行简化,将黑启动电源及其附近重要发电厂、重要恢复目标合并, 形成初始分区;分裂过程是在凝聚过程的基础上采取GN分裂算法确定简化后的电网的恢复分区。通过模块度Q值和电气特性两方面对恢复分区进行校验,判断分区划分的合理性。校验通过后,采用Floyd算法寻找分区内机组间恢复的最短路径。
- 以IEEE10机39节点系统为例,验证本文提出的分区方法和最短路径恢复方法。算例结果表明,本文提出的方法能较好的处理电网大停电后的恢复分区问题,且可以参考最短恢复路径上的节点位置,调整重要负荷的位置,使其位于最短恢复路径上,这样可以尽快对重要负荷恢复供电,从而可以减少经济损失。
最后,对本文所做的研究工作进行总结,并简要地展望了有待进一步研究的问题。
复杂网络社团结构
2.1 引言
复杂网络是指将组成复杂系统的构成单元抽象成节点、将各单元间的关系抽象为边后所形成的一个有n个节点和m条边的拓扑图,复杂网络是研究复杂系统的一种角度和方法。自Watts等人于1998年发表《“小世界”网络的集体动力学》[28]及 Barabasi等人于1999年发表《随机网络中标度的涌现》[29]后,复杂网络理论就广泛地运用到了各个领域。例如,用于研究某传染病毒在人群中的传染机制;用于研究流言蜚语在社会中的扩散;用于研究金融危机的爆发过程等。近年来,复杂网络理论也逐渐应用到电网的研究中,主要在电网的小世界模型特性[30],电网脆弱性评估[31-32],连锁故障传播机理[33-34]等方面进行研究。
社团结构是指在网络中具有共同特征的顶点所组成的集合,它将网络划分成多个区域,各个区域的内部联系紧密,外部联系稀疏。对电网进行恢复分区划分的目的是大停电后分别对分区进行恢复,待各分区都恢复完成后,再对各分区进行同期并列,其特点是分区内部联系较为紧密,分区之间的联系较为单一和稀疏,这一特点与复杂网络的社团结构的特点相似,因此可以考虑用复杂网络的社团结构理论作为恢复分区的划分的理论基础。
2.2 复杂网络理论的基本概念
近年来,人们提出了许多表征复杂网络的特性的概念和方法,其中包括:度和度分布、最短路径、介数、聚类系数等。在对社团结构划分结果的评估上主要有两类:一类是已知网络的社团结构划分结果,一般用NMI(Normalized Mutual Information)和ARI(Adjusted Rand Index)去衡量算法划分结果和真实结果的重合程度;另一类是不知道网络社团结构的划分结构,一般用模块度(Modularity)Q函数来衡量社团结构划分的优劣。 本文主要介绍度与度分布、最短路径、介数和模块度(Modularity)Q函数这几个在本文的研究中将会使用的参数的基本概念。
2.2.1 度与度分布
在复杂网络中,度定义为和某一节点相连的其他节点的数目,节点 的度的表达式为
的度的表达式为
 (2-1)
(2-1)
其中, 是邻接矩阵
是邻接矩阵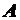 中第
中第 行第
行第 列元素。一般来说,一个节点的度越大就意味着这个节点越重要。
列元素。一般来说,一个节点的度越大就意味着这个节点越重要。
度分布 是指在网络中任意选择的一个节点
是指在网络中任意选择的一个节点 ,它的度恰好为
,它的度恰好为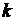 的概率,也就是表示节点
的概率,也就是表示节点 有
有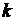 条边与其相连的概率,表达式如(2-2)所示。常见的度分布有两种形式:一种是指数分布,即
条边与其相连的概率,表达式如(2-2)所示。常见的度分布有两种形式:一种是指数分布,即 是
是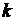 的指数函数,另一种是幂律分布,即
的指数函数,另一种是幂律分布,即 是
是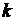 的幂函数
的幂函数
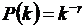 (2-2)
(2-2)
其中,为度指数
2.2.2 最短路径
在复杂网络中,某一节点 到达另一个节点
到达另一个节点 的所有通路集合为
的所有通路集合为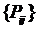 ,其中集合中长度最短的通路就是节点
,其中集合中长度最短的通路就是节点 到节点
到节点 的最短路径。一般来说,网络中的最短路径也是网络中的最优路径,寻找最短路径的方法主要有Dijkstra算法、A*算法、Bellman-Ford算法、Floyd-Warshall算法等。
的最短路径。一般来说,网络中的最短路径也是网络中的最优路径,寻找最短路径的方法主要有Dijkstra算法、A*算法、Bellman-Ford算法、Floyd-Warshall算法等。
2.2.3 介数
介数是复杂网络中衡量节点或者边的另一重要指标,通常分为边介数和节点介数两种。节点介数是指网络中所有最短路径中经过该节点的路径的数目占最短路径总数的比例,其计算公式为
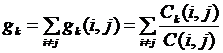 (2-3)
(2-3)




