摘 要

本文介绍了一种基于智能算法的无线输电系统参数识别方法，该方法使用径向基函数神经网络作为算法模型，以无线输电系统的输入端电压的幅值和频率、输入端电流的幅值和相角作为样本特征值，预测出系统接收端电阻值和电容值大小，从而避免在接收端测量的复杂工作。算法使用的样本数据是通过系统矩阵方程计算出准确值后，再添加一定幅值的噪声生成的，与无线输电系统实际运行参数接近。径向基函数神经网络训练过程分为样本中心点位置计算和权重值优化两部分，其中样本中心点位置计算采用k均值聚类算法，而权重值的优化采用带动量的自适应学习率梯度下降算法。算法最终测试结果表明，径向基函数神经网络能够以较高的精度实现无线输电系统参数预测，并具有一定的抗干扰能力，泛化性能良好，可以在实际无线输电系统中应用。本文最后总结了算法的适用范围，并提出了算法需要改进之处和可能的改进方法。

关键词：无线输电系统；参数识别；神经网络

Abstract

In this paper, a method of parameter identification for wireless power transfer systems based on intelligent algorithms is introduced. Using the amplitude and frequency of the input voltage, the input current amplitude and phase angle as features, the radial basis function neural network algorithm model is used to predict the resistance and capacitance values of the receiving end of the system. This method can avoid the complex work of measurement at the receiving end. The sample data used by the algorithm is generated by adding the noise of a certain amplitude after calculating the exact value by the system matrix equation, which is close to the actual operating parameters of the wireless power transfer system. The radial basis function neural network training process is divided into two parts: sample center point calculation and weight value optimization. The k-means clustering algorithm is used to calculate the center position of the sample, and the gradient descent algorithm of adaptive learning rate is used to optimize the weight value. The final test results of the algorithm show that the radial basis function neural network can predict the parameter of wireless power transfer system with high accuracy, and has a certain anti-jamming capability, which can be applied in practical wireless power transfer systems. At last, this paper summarizes the scope of application of this algorithm, and proposes the shortcomings and improvements of the algorithm.

Key Words：wireless power transfer system；parameter identification；neural network

目 录

第1章 绪论 1

1.1 研究背景 1

1.2 研究目的及意义 1

1.3 研究内容 1

第2章 样本数据计算及预处理 2

2.1 无线输电系统模型及计算 2

2.2 数据预处理 3

2.2.1 样本中添加噪声 3

2.2.2 划分子集 3

第3章 神经网络模型及参数优化 5

3.1 神经网络模型 5

3.1.1 感知器 5

3.1.2 人工神经网络结构 6

3.1.3 径向基函数神经网络 8

3.2 参数优化方法 9

3.2.1 k均值聚类算法 10

3.2.2 梯度下降算法 11

第4章 算法测试结果及分析 16

4.1 算法测试结果 16

4.2 结果分析 19

第5章 总结 21

参考文献 22

致 谢 24

第1章 绪论

1.1 研究背景

无线电能传输技术是美国物理学家Nikola Tesla在上个世纪提出的，由于当时设备及技术的限制未得到实现。随着社会和科学技术的发展，无线电能传输技术已经逐渐变得成熟，也出现了各种不同的无线输电系统。到目前为止，无线电能传输技术已经能够使用多种能量传输方式实现，常用的是磁感应耦合[1]和电磁谐振耦合[2-4]，其他传输方式还有电场耦合[5]、微波[6]、激光以及超声波等。其中，电磁感应式通常用作短程无线电能传输，而磁耦合谐振技术则适用与中远程无线电能传输。基于磁耦合谐振技术的无线输电系统具有传输距离远、效率高的优点，近年来成为主流的无线输电技术。

基于磁谐振耦合技术的无线电能传输系统是利用“共振”的原理：对于空间中具有相同自谐振频率的一系列线圈，如果发送线圈的激励源频率恰好在自谐振点，则收发线圈间耦合强度最大，从而可实现电能的最佳传输。为了使系统达到尽可能高的负载功率和传输效率，需要根据发送线圈与接收线圈之间的耦合系数选择合适的系统共振频率[7,8],并根据耦合系数进行阻抗匹配[9]。耦合系数与系统元器件参数相关，因此，为了确定系统运行在最优工作点，必须获取系统参数，再进行调节。

1.2 研究目的及意义

一般情况下，系统拓扑结构固定，在不考虑系统两端通信的情况下，如果要获取接收端的电路参数，采用实时采集测量的方法较为复杂，测量成本高。发送端由于调整工作点需要采集电压、电流信息，因此考虑以采集到的输入端电压、电流信息估计出所需的接收端电路参数。部分负载参数可以直接使用输入电压、电流通过系统矩阵方程解出，但是求解矩阵方程对系统计算能力要求比较高，实时计算系统参数有一定的困难。另一种方法是采用智能优化算法[10]，分析输入电压电流与输出之间的对应关系，通过这种对应关系估计出系统参数，可避免复杂的运算。因此本研究需设计一种无线输电系统参数识别方法，使用系统输入端电压、电流信息估计出系统接收端参数，避免了从接收端采集信息的麻烦，并具有更快的响应速度，以便于系统实时调整工作点，保持最大传输效率或负载功率。

1.3 研究内容

本研究的主要内容：首先通过无线输电系统矩阵方程得到算法所需的训练样本，对训练样本进行简单处理，然后建立神经网络算法，通过比较选择合适的网络模型和参数优化算法，最后通过计算此模型预测结果与实际值之间的误差，验证算法的实用性。

第2章 样本数据计算及预处理

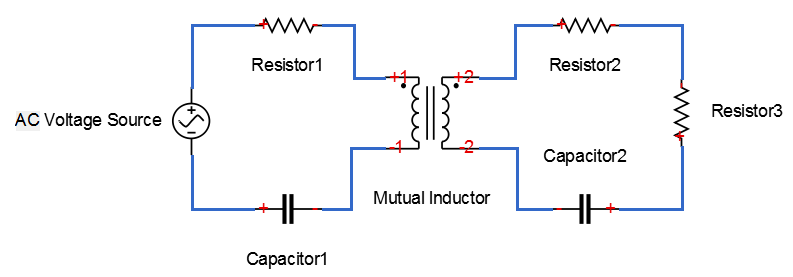2.1 无线输电系统模型及计算

基于磁耦合谐振的双线圈无线输电系统模型如图2.1所示。

图2.1 双线圈无线输电系统模型

系统可由以下矩阵方程表示：

(2.1)

其中，为系统输入电压，、、分别为输入端电阻、发送线圈自感和电容大小，、、分别为接收端电阻、接收线圈自感和电容大小，和是两个线圈之间的互感大小。

根据上面的无线输电系统模型，给定系统所有元器件参数，改变输入端电源电压大小和频率，解矩阵方程可得多组和的值。在计算可用的样本数据之间，需要先确定给定元器件参数的合理范围，因为系统参数不合理时，可能会使接收端电流过小或过大，样本没有实际意义，或者使系统状态发生变化，导致以上方程不再适用等问题。确定参数合理范围的方法是参考实际无线输电系统，或先设定一组参数，计算系统输入输出是否正常。

由于算法训练需要较多的样本以提升泛化性能，矩阵方程中电源输入电压大小、频率、负载阻值、接收端的电容大小都需要在一定范围内变化，得到均匀分布的样本。对于电容、电感和输入电压幅值，这些参数实际变化范围较小，可以设置为较小的计算范围，而负载阻值、输入电压频率会出现较大变化，为覆盖尽可能大的取值范围但不增加太多样本数量，负载阻值和频率的样本步长较大。

2.2 数据预处理

按照以上步骤得到的一系列样本还不能直接用于算法模型的训练，因为这些数据是有一定顺序结构，并且是准确计算的值，和系统实际运行时采集到的带有各种误差、离散的值不同，因此需要对这些样本进行预处理。

2.2.1 样本中添加噪声

实际应用中算法的输入是带有测量误差的数据，为了提高算法的抗干扰能力，应该在训练时使用带有噪声的数据，这样会使算法模型的训练更加困难，但实际运行效果更好。

向样本中加入的噪声是随机的，但一般认为样本误差服从正态分布，因此设定误差在计算结果的范围内波动即可，带噪声的样本数量与标准样本数量比例为。

2.2.2 划分子集

一般将训练时算法预测值与期望输出(训练样本实际值)之间的误差称为“经验误差”，算法训练完成后，输入训练样本以外的新样本得到的算法预测值与期望值之间的误差称为“泛化误差”，因此经验误差是训练过程中用来判断算法优化程度，而泛化误差则是评价算法模型实际表现的重要因素。在训练过程中，输入训练样本来优化算法参数，只能获得经验误差并尽可能使其达到最小值。如果将拥有的所有样本数据用作训练，直接使用经验误差来评价模型效果，则可能导致算法经验误差很小，但在输入训练样本以外的新样本时预测误差与样本真实值之间误差很大，即泛化误差很大，这种情况称为“过拟合”。过拟合出现的原因之一是算法训练过程中为了将经验误差最小化，学习到了样本数据中带有的特有性质，这些性质并不是算法优化对象所具有的“一般性质”。为了避免出现过拟合，算法训练前需要先将已有的样本数据划分为互斥的子集。通常将样本划分成三个互斥子集分别作为训练集、验证集和测试集，验证集用于模型的选择，本研究不考虑多种算法模型的选择，因此样本只需要分成训练集和测试集。

数据集的划分有多种不同方法，其中常用的有留出法和交叉验证法。留出法是将数据集通过分层采样的方式分成训练集和测试集，其关键在于保证在采样过程中不引入新的分布。本研究算法中使用的输入量变化并非线性，使用留出法划分子集无法保证训练集与对象真实分布完全一致，并且单次留出法划分并不一定可靠，因此只能进行多次划分求平均值来保证更小的出错几率，但这样做增加了训练难度。交叉验证法先将样本分成n个互斥的子集(保证不引入新的分布)，然后分别以其中一个子集为测试集，其他子集为训练集进行算法模型的训练，求此n次训练所得的平均结果。交叉验证法进行子集划分时与留出法存在同样的问题，因此也需要进行多次取平均。

显然，数据集的划分会带来训练上的难度增大，但这是必要的。本研究设计的算法模型输入特征有四个，按照每个特征10组的大小估计样本数量也会达到一万以上，此时使用交叉验证法的训练成本太大，因此使用留出法，重复次数根据最终模型单次训练时间可以进行人工调节。

第3章 神经网络模型及参数优化

3.1 神经网络模型

神经网络[11]是一种具有强大的非线性学习能力的算法模型，被广泛用于分类、函数拟合、模式识别、目标检测、图像处理等领域。与生物的神经系统类似，神经网络模型由多个神经元按照一定的连接规则组成，信号在传递过程中激活其中一部分神经元，根据信号传递的路径不同最终输出可以是一个或多个。下面先介绍单个神经元的模型特性，再分析由多个神经元组成网络时的不同结构，以选择合适的神经网络模型。

3.1.1 感知器

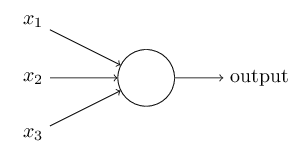感知器即单个神经元模型，一个神经元包括树突(输入)、细胞主体(计算单元)、轴突(传递信号)，如图3.1所示：

图3.1 感知器模型

图中、、为输入，实际输入个数可以是任意个，输入量在传递到计算单元之前，各自乘以独立的权重值、、，计算单元对带权重的输入信号进行处理。根据目标输出的不同，计算单元的处理方法不同，这些处理方法称为激励函数。通常情况下，若输出是线性变量，激励函数也是线性的，如求和输出；若输出值是离散型变量，一般通过S型函数将输出离散化；另外还有只在某个区间内连续的激励函数。

当激励函数为线性求和函数，由上面的分析可知感知器模型相当于完成了线性映射算法，可以完成线性回归分析。当激励函数设定为S型函数(即在某一点或较小的区间内连续，其余取值为离散值的函数)时，感知器可以完成对线性可分样本的分类任务。由此可知，单个感知器只能完成样本的线性预测或将线性可分的样本分类或映射成离散值这样的工作，这对于一般的函数拟合和分类任务是远远不够的，如本研究任务中，输入变量变量与输出之间的关系就是非线性的。

实际上使用感知器实现非线性连续函数的拟合并非完全不可行，但需要对样本特征进行处理，使感知器的输入与输出之间转换成线性相关。特征处理方法有很多种，例如多项式映射、核空间映射等。多项式映射指的是指的是将所有样本的原始特征映射到更高次的多项式空间，使得样本加入这些输入特征之后与输出成为线性关系。例如函数，原始特征为x，y与特征x为非线性关系，多项式映射后样本输入特征为x和，这时输出与特征之间就转换成了线性关系。另一种方法是通过核函数映射，预测对象与样本特征在原始空间上是非线性关系，但是可以通过将特征映射到其他空间，在其他空间里预测对象与样本特征之间是线性相关的，多项式可以看作是一种核函数，还有其他常用的核函数如高斯核函数等。对样本原始特征进行映射处理在样本数量少的情况下效果较好，支持向量机算法通常就是采用这种方法解决非线性问题，但在数据量较大时，样本映射到高维空间就会变得非常困难。考虑到本研究需要更快的运行速度，因此不使用这样处理方法实现。

3.1.2 人工神经网络结构

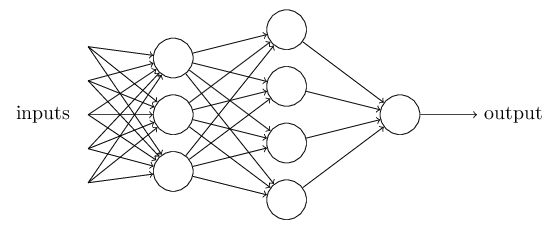将多个感知器进行组合形成网络结构，类似于生物神经系统，就是人工神经网络，模型如图3.2所示：

图3.2 人工神经网络模型

其中，第一层为输入层，直接传递样本特征值或带权重的特征值，中间的所有层为隐藏层，传递经过中间神经元处理的并带有权重的信号，最后一层为输出层，负责计算并输出最终结果。输入层的神经元个数通常与样本数量或特征数相等，而隐藏层的数量和每个隐藏层包含的神经元个数都是任意的，需要调整优化，输出层神经元数量则与输出量有关，可以为一个或多个。

网络中的所有神经元激励函数都可以不相同，神经元之间的连接也有多种方式，因此神经网络可以形成多种不同的模型，如线性神经网络、径向基函数神经网络、玻尔兹曼机、卷积神经网络、循环神经网络等。使用特殊的激励函数(如S型函数)时神经元能够将输入的信号离散化，这是神经网络非线性学习能力强的原因，而使用线性激励函数则能够实现局部信号的加权线性组合。每个隐藏层神经元的输出都可以看作是该神经元从输入信号中提取出的抽象的特征，因此信号每经过一层，得到的就是更利于模型预测的特征。根据预测对象的不同，可以选择合适的激励函数和隐藏层数量构成特定的神经网络。

由以上的分析可知，神经网络模型除了结构以外，需要人工调节和优化的参数是与激励函数相关的参数和每一层输出的连接权值。需要训练的参数数量会随着网络中包含的神经元数量和层数的增加而增加，因此能够保证预测任务完成的情况下应该选择更加简单的网络结构，降低模型训练成本。无线输电系统参数识别问题属于连续值预测，由矩阵方程2.1可知输出量与输入特征之间为非线性关系，可以用多元高阶函数表示，因此选择能够拟合复杂非线性函数的神经网络即可。

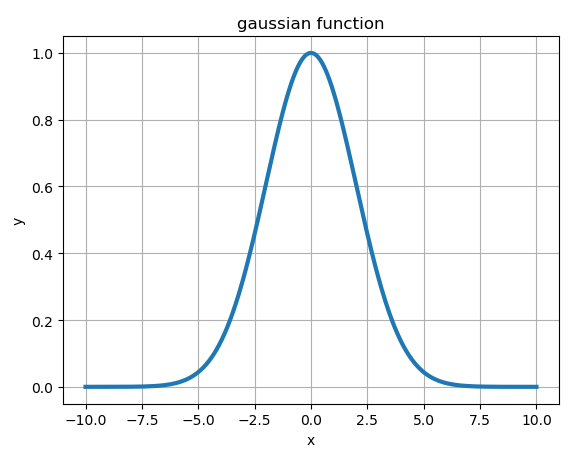
不进行原始特征处理的情况下，神经网络实现非线性预测至少需要一个隐藏层来提取非线性特征，一种方法是将隐藏层激励函数设定为S型函数，如sigmoid函数：

(3.1)

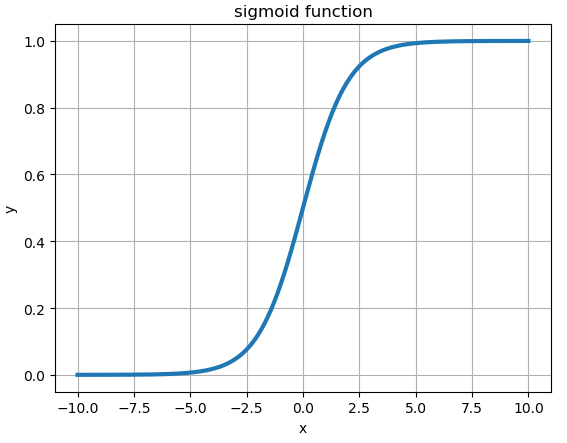函数图像如图3.3所示：

图3.3 sigmoid函数图像

由图3.3可知，sigmoid函数在[-4,4]区间上单调递增，函数值在0到1之间，在(-∞,-4)区间上函数值趋近于0，(4, ∞)区间上趋近于1。利用这个性质可以使输入的连续值离散化为0和1。在实现分类任务时，隐藏层神经元经常使用S型函数使中间层传递的信号离散化。因此，要实现非线性函数拟合，隐藏层所有神经元可以使用S型函数，在输出层再把隐藏层信号求和并增加截距项，最终输出结果就是连续值。

S型激励函数通常用于分类模型，以这种方式建立神经网络虽然能够完成本研究中的函数拟合的任务，但其精度的不足需要依靠隐藏层神经元数量和隐藏层数来提高，原因在于S型激励函数能够学习到输入的离散性高维特征，而在无线系统参数识别的任务中，实际上输入与输出之间并不存在离散性的特征，模型只是通过足够多的离散变量来拟合出这个函数曲线，因此选择这种结构完成函数拟合任务并不合适，下面介绍另一种神经网络结构，称为“径向基函数神经网络”，这种网络结构具有更强的非线性函数逼近能力。

3.1.3 径向基函数神经网络

径向基函数神经网络[12,13]一共分为三层，即除了人工神经网络必须的输入层和输出层以外只有一个隐藏层，输入层直接传递样本特征值(不带权重)，隐藏层神经元使用径向基函数作为激励函数，输出层则是隐藏层输出信号的线性组合。径向基函数是指函数值只与输入变量与某一个中心点之间的距离有关的函数，即：

(3.2)

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：