摘 要

基于Ansys的拓扑结构优化平台的开发是为了结合专业的有限元分析软件Ansys和高性能的数值计算软件Matlab，使得双向渐进结构优化法（BESO）能够应用于具有复杂设计域几何外形的二维和三维拓扑优化设计问题。

在Ansys中建立有限元模型并完成有限元计算，得到单元信息，并根据单元信息进行灵敏度计算，根据灵敏度信息应用BESO算法进行设计变量的更新，经过多次迭代计算可以得到最后的拓扑解。

采用BESO算法（双向渐进结构优化法），依托Matlab平台实现拓扑优化。BESO算法通过有限元仿真分析结果，经过灵敏度分析得到有限元单元对于结构整体刚度的贡献值，依据灵敏度权重逐步消除和增加结构单元，直至获得局部最优结构构型。

测试算例选用了二维的悬臂梁，轮辐结构，三维悬臂梁及三维控制臂等的刚度优化设计，算例结果均可在指定的体分比约束条件下实现结构构型的刚度最大化设计。

关键词：拓扑优化，双向渐进拓扑优化，Ansys，Matlab

Abstract

The development of Ansys-based Bi-directional evolutionary structural optimization design platform combine Ansys, a professional finite element analysis software, with Matlab, a high-performance numerical calculation software. So that, Bi-directional evolutionary structural optimization (BESO) can be applied to 2d and 3d topology optimization design problems which design domain is a complex geometry shape.

We build the finite element model and do the finite element analysis in Ansys, then get the element information, and the sensitivity number is calculated on the basis of this element information. According to the sensitivity number, using ESO algorithm for update of design variables, we can get the final topology solution after several iterative calculation.

We adopts the BESO algorithm (Bi-directional evolutionary structure optimization method), which is realized by Matlab platform, to finish the topology optimization. BESO method through finite element simulation analysis, sensitivity analysis to obtain the element for the contribution of whole stiffness value, according to the sensitivity weight gradually eliminate and increase the structural element, until you get the local optimal topological structure.

The test case of this design platform is stiffness optimal design in two-dimensional cantilever beam, the spoke structure, three dimensional cantilever beam and the three dimensional control arm, this several example results can get the topological structure that realize the maximization of the stiffness under the specific volume fraction.

Key words: topology optimization, BESO, Ansys, Matlab

目 录

第1章 绪论 1

1.1 研究目的和意义 1

1.2 国内外研究现状 1

1.3 主要内容和技术方案 2

第2章 BESO法的理论概述 4

2.1 刚度优化问题下BESO法的数学模型 4

2.2 BESO法的网格依赖性 4

2.3 BESO法的设计变量更新 6

2.4 本章小结 7

第3章 设计平台的具体实现 8

3.1 Ansys有限元模型的前处理与有限元求解分析 8

3.1.1 有限元模型的构建 8

3.1.2 有限元模型的求解分析 8

3.2 Ansys与Matlab的信息数据共享交流 9

3.3 BESO算法的Matlab代码编写 9

3.3.1 参数设定及有限元模型的构建（1-11行） 9

3.3.2 过滤权重因子的计算（13-29行） 10

3.3.3 拓扑优化的循环迭代（30-70行） 10

3.3.3.1 敏度过滤 10

3.3.3.2 设计变量的更新 11

3.3.3.3 输出设计变量 11

3.4 本章小结 11

第4章 结构刚度优化问题测试算例 12

4.1 二维结构刚度优化问题算例 12

4.1.1 half_MBB梁的结构刚度优化 12

4.1.2 空心悬臂梁的结构刚度优化 14

4.1.3 轮辐结构的结构刚度优化 15

4.2 三维结构刚度优化问题算例 16

4.2.1 三维悬臂梁的结构刚度优化 16

4.2.2 三维控制臂的结构刚度优化 18

4.3 本章小结 22

第5章 结论 23

致谢 24

参考文献 25

附录 29

附录A： FE_model的apdl命令流 29

附录B： FE_solve的apdl命令流 32

附录C： Matlab算例代码 34

第1章 绪论

1.1 研究目的和意义

本毕业设计选题为《基于Ansys的渐进结构拓扑优化设计平台开发》，目的是借助双向渐进结构优化法（BESO），以Matlab为主设计平台，调用Ansys作有限元分析，并在Matlab中读入求解结果，并分析修改设计变量来改变结构构型，最后通过迭代求解计算来完成结构拓扑优化。

针对于刚度拓扑优化问题的实现，夏凉等人^[2]参照基于变密度法的88行Matlab程序代码^[1]给出了BESO法的Matlab程序代码“esoL.m”。该程序代码可实现二维长方形设计域结构构型在以材料用量为约束条件下的刚度最大化设计。由于Matlab软件虽然是一款高级的编程计算软件，但是它并不是一款专业的建模软件，因此基于Matlab平台编写的“esoL.m”程序代码对于设计域的几何外形具有局限性，例如网格划分只可以使规则的正方形网格，而且不易于开展具有复杂几何外形的三维结构构型的拓扑优化设计。而Ansys是一款性能优异的有限元分析商业软件，其建模、网格划分、有限元分析等功能强大，且拥有丰富的命令流命令，但是其自带的拓扑优化变量更新算法在应用过程中不够直接和高效。本设计平台主要结合使用了Matlab与Ansys这两款软件。通过结合Ansys与Matlab，就可以利用Ansys的模型处理及有限元分析的功能与基于Matlab平台的BESO更新算法形成一个优势互补，能够有效的将BESO法应用于复杂几何构型的结构设计问题。再者，当拓扑优化的目标函数变化时，利用Ansys强大功能，简单地把分析所得数据引入Matlab中，并对BESO法更新算法代码进行相应的修改，会更加容易地进行不同目标下的拓扑优化。这个正正就是这个基于Ansys渐进结构拓扑优化设计平台开发建立的意义所在。

1.2 国内外研究现状

本毕业设计是需要建立一个完成拓扑优化的平台，而拓扑优化是指在给定的负载情况、约束条件和性能指标下，在给定的区域内进行对材料分布进行优化的数学方法。而拓扑优化研究已经有100多年的发展历史，早期的拓扑优化研究可追溯到由澳大利亚的学者Michell^[3]所提出的桁架布局轻量化设计的最优标准。而70年后Rozvany等人^[4]-[6]对Michell的理论进行了延伸，准确地分析了在网格结构下该桁架问题的全局最优解。随着计算能力的提升及数值仿真方法的深入研究，学界开始进行对拓扑优化问题的数值研究。在连续体的结构设计问题中，拓扑优化可以被定义为一个离散的问题或者一个仅仅是由实体的材料或空洞组成的二元设计问题。然而，结构刚度优化设计并不适合这种二元设置，其优化出来的可行设计解是存在不收敛性的^[7]-[10]。Bendsøe and Kikuchi^[11]提议使用均匀化理论，在一个离散的局部区域内假定材料由多孔微结构构成来缓和这个问题，使得此收敛性问题得到了较好的解决，数值拓扑优化也因而获得了阶跃性的发展。自此之后，拓扑优化领域出现了不少方法，例如：均匀化法^[12]，变密度法^[13]-[14]，渐进法^[15]-[16]，泡沫法^[17]，拓扑导数法^[18]，水平集方法^[19]，相场法^[20]以及我国学者隋允康等人提出的独立连续映射法^[21]。而渐进结构优化（ESO）方法作为拓扑优化的一个重要分支，最初是基于Xie等人^[15]-[16]所提出的一个简单概念，及通过逐步去除结构中低效的材料，最终使结构逐渐趋于最优构型。ESO方法也因此被认为是一种单元硬杀算法，也就是说删除了的单元会被永久删除，不会再在拓扑结构中恢复。Querin等人^[22]-[24]开发了双向进化结构优化(BESO)方法的早期版本，该方法允许恢复与高效的单元相邻的早期被删单元。ESO方法的另一个主要发展是黄晓东和谢亿民^[25]所提出的去除网格依赖性的BESO法，它采用了一种灵敏度过滤器方案来实现网格独立，以及利用历史信息来稳定灵敏度数据以求更快达到收敛。该方法的最新版本在应用广泛的结构设计问题时表现出了良好的性能，包括刚度和频率优化^[26]，非线性材料和大变形^[27]-[28]，能量吸收^[29]，多材料^[30]，多重约束^[31]，周期结构^[32]-[34]等。由于渐进结构优化法的高效性和稳健性，在学术研究及工程实践上都有了广泛的应用。所以本毕业设计计划采取双向渐进结构优化法（BESO）来进行结构拓扑优化设计。

HyperWorks Optistruct和Tosca均是业界知名的拓扑优化商业软件。两者均采用的拓扑优化方法为变密度法，它们均可实行各种工况下的多目标优化分析，且拥有并行运算功能提高计算效率。而Optistruct具有强大的细节优化能力，它可在多种工况下进行细致化的拓扑优化。Tosca的拓扑优化模块也拥有自己独立的优化模块,可以在给定工况下优化出性能不错的拓扑优化构型。对比着来看这两款软件，Optistruct可采用Hypermesh作为前处理器，在各大行业内都得到较多的应用；Tosca的开放性很强，使用起来比较方便，它可支持所有主流求解器的前后处理的读入。而Ameba所采用的拓扑优化方法是双向渐进结构优化法（BESO），这也是BESO法在商业软件上的首次应用。Ameba拥有自己的三维建模模块，可直观地展示每一步迭代的拓扑构型。但不足的是目前Ameba的功能还不够强大，仅可以就刚度问题进行很好的优化求解。

1.3 主要内容和技术方案

本毕业设计针对于刚度优化问题，学习吸收夏凉等人^[2] 所给出的BESO法的Matlab程序代码“esoL.m”。以Matlab作为主设计平台，通过调用Ansys进行有限元分析，基于有限元分析得到的单元信息计算设计变量迭代更新所需的单元灵敏度，并利用此作为优化判据，通过BESO算法更新零件设计区域的设计变量。迭代进行有限元分析及算法更新，若干次迭代计算后就可以得到收敛的拓扑优化解。预期此平台可以进行二维及三维刚度问题的拓扑优化。

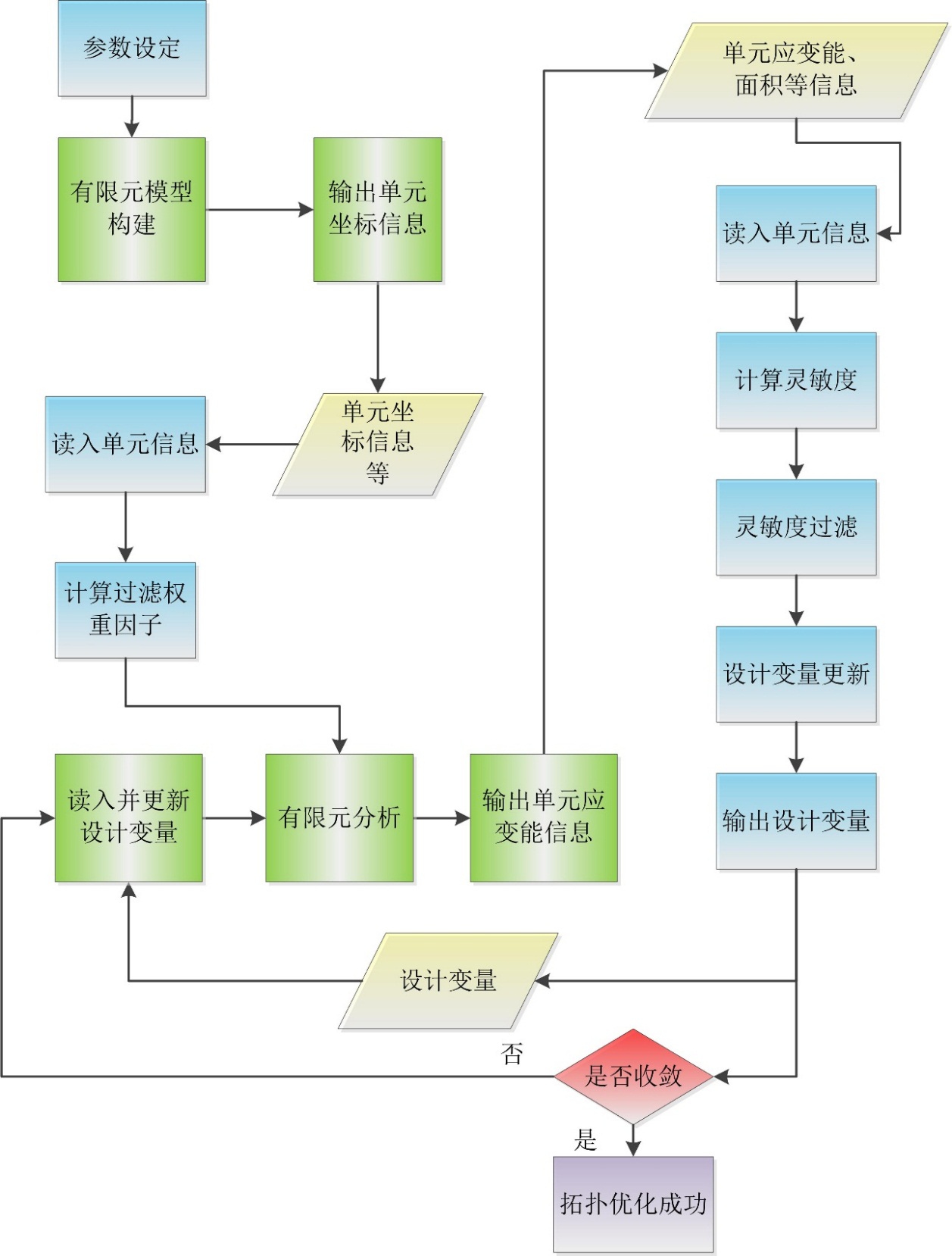
图1.1 设计平台构建流程图

本设计平台构建的流程图如图1.1显示，其中绿色框内流程需要调用Ansys完成，蓝色框内流程需要在Matlab中完成计算，黄色菱形方框内的信息是需要在Ansys与Matlab中共享的数据信息。

第2章 BESO法的理论概述

2.1 刚度优化问题下BESO法的数学模型

对于基于BESO法的结构刚度最大化问题，目标为实现最大化刚度，约束为材料体积容积约束，具体的数学表达式如下：

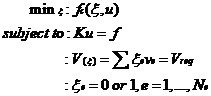
其中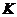和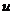为全局结构刚度和位移矢量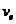，为单元体积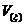，和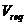分别为整体材料体积和需求的材料体积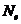，为设计变量总数。与单元存在与否相关的单元 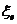表明为单元缺失（0）或单元存在（1）。

按照BESO法的理念，在将单元材料移除出或添加到当前设计域之前，需要先给定当前迭代过程的目标体积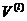。由于所需的材料体积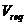通常是比初始猜测的设计体积小，因此每次迭代中的目标体积可能会逐步减少，直到实现体积约束。体积的变化可以通过下式表示:

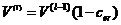
在迭代过程中，进化率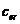决定了从上一次迭代所产生的拓扑构型中添加或删除材料的百分比。直到达到了目标需求的材料体积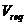，优化算法就只会改变拓扑构型，但在一定的容差范围内保持体积不变。

在每一次迭代过程中，用单元的敏度值来表示该单元在结构中效率高低的相对等级，而此敏度值用于确定材料的移除和添加。而刚度优化问题的目标敏度值被定义如下：

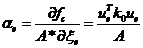
其中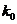为单元刚度矩阵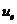，为单元位移矢量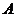，为单元面积

对于BESO法才说，对于敏度数据还需要进行一次过滤，以避免所求出来的拓扑结构趋于收敛及更直观的求解结果。

2.2 BESO法的网格依赖性

几乎对于所有的拓扑优化方法来说，网格依赖问题是一个常见的问题^[35]。这个问题的主要原因是在于引入更多的孔总是可以使设计更加高效。这种效应被看作为存在数值不稳定性，即当使用更精细的有限元网格时，会出现更多的孔。

为了解决这个问题，参考Huang and Xie^[25]所提出了一种改进方法。首先，采用过滤方案以确保结果的存在，同时避免棋盘化现象(见图2.1)和网格依赖问题;其次，利用历史信息对灵敏度进行修正，以稳定优化过程。

图2.1 BESO法中经典的棋盘格现象

为了避免网格依赖性和棋盘模式,过滤方案首先平滑了敏度数据

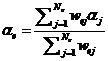
其中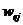为线性加权因子

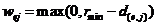
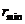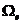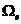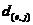根据程序规定的过滤半径和单元中心到另一单元中心的距离所确定的。

可以猜想到，通过此过滤方案，平滑了整个设计区域中的敏度值。因此可以自动获取空单元的敏度值。由于临近拥有高敏度值的实体单元，空单元或许会拥有较高的值。故在下一次迭代中一些空单元就会转化成实体单元。图2.2可直观的表示过滤半径分别为1.5倍单元长度l_e与3倍单元长度l_e的空单元相应的数值。虽然此过滤方案是纯启发式的，可是通过这个简单的方案，许多拓扑优化上的数值问题，如棋盘格和网格独立问题可以得到有效的解决。由此生成的结果与在应用局部梯度约束^[36]所得结果相似。而且这个过滤器只需要较小的额外计算时间并且可十分容易地在优化算法中实现。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：