摘 要

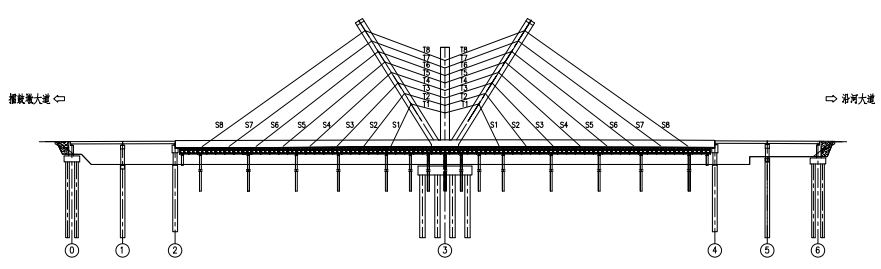
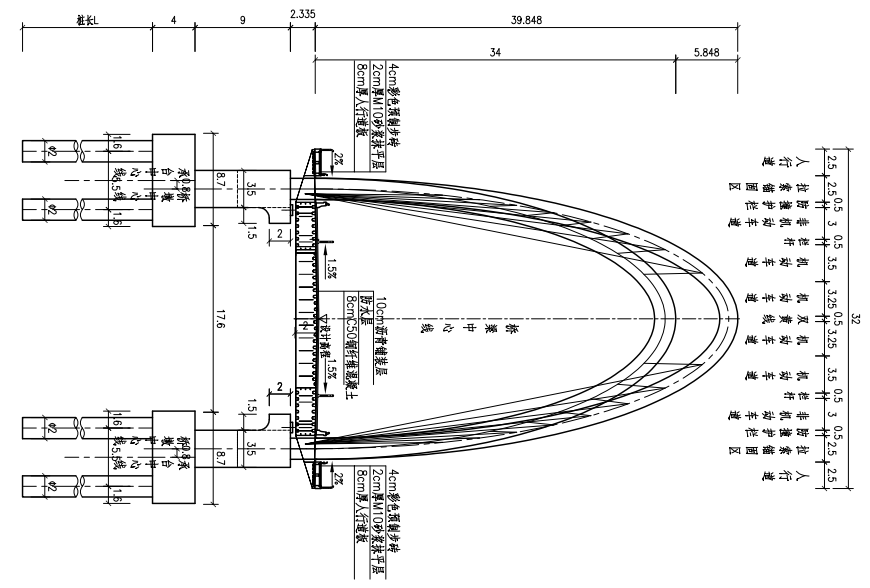
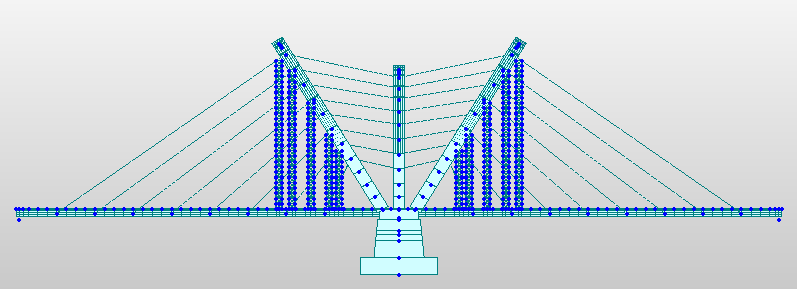
随着人们在精神文化层次上的不停追求，工程师们对城市景观桥梁的设计有了更多的想法，一些造型独特的桥梁形式由此应运而生。本文的研究对象是多段索异型塔斜拉桥，即桥塔为主、副塔组成的拱形组合独塔，由主、副塔之间的塔间索及主塔、主梁间的塔梁（斜拉）索组成的多段索构成了复杂空间索面。该桥的独塔结构不同于一般独塔斜拉桥，其刚度受塔间索索力的影响较大，同时多段索间存在复杂相互影响，使得这种桥型结构的成桥索力、施工阶段张拉力求解和索力调整计算异常繁琐。本文在现有斜拉桥合理成桥状态计算方法的基础上，采用MIDAS/CIVIL软件提出了求解多段索异形塔斜拉桥合理成桥索力的分步实用算法。针对该类桥施工过程中的索力控制问题，对比了正装、倒拆、无应力状态法等计算方法，摸索了一套结合无应力状态法求解此类桥梁施工阶段拉索张拉力的方法，极大地简化了施工过程中由于张拉顺序等变化而导致的繁琐索力调整计算，拓展了无应力状态法控制理论在该类桥型中的应用。该实例桥的数值分析结果表明，本文的方法是有效的，对于该类桥型的施工监控工作具有重要的指导意义。

关键词：多段索异型塔斜拉桥；复杂空间索面；成桥索力；施工阶段索力；无应力状态法

Abstract

With the improvement of people's demand for spiritual needs, cities have raised higher requirements for the design of bridges, encouraging the appearances of unique cable-stayed bridges. This paper concentrates on a cable-stayed bridge with not only complex space cable plane but also a special-shaped bridge tower. To be exact, this arched bridge tower includes 2 main towers and one auxiliary tower while stayed cables includes some between the main towers and the girder, and others between towers. This bridge is far different from the ordinary single tower cable-stayed bridge mainly because the stiffness of bridge tower is greatly influenced by the cable tensile force between the towers. In addition, there is a complex interaction between those stayed cables, which makes it difficult to determine rational construction state and reasonable completion state. On the basis of the existing calculation method of cable tensile force, this paper puts forward a step algorithm which used MIDAS/CIVIL for deducing the cable tensile forces of reasonable completion state. Besides, in order to control the cable tensile forces in the construction process, this paper deduces the cable force of every construction state by method of Unstressed State Control, after comparing with methods like Forward-iteration method, etc. It greatly simplifies the complicated adjustment calculation, and the application scope of Unstressed State Control is extended. Numerical analysis results show that the two methods mentioned above are effective and of great significance for the construction monitoring of this type of bridge.

Key Words：special-shaped bridge tower；complex space cable plane ；cable tensile forces of completion state ；cable tensile forces of construction state；Unstressed State Control

目 录

第一章 绪论 7

1.1 复杂空间索面异形塔斜拉桥发展概况 7

1.2 斜拉桥索力计算方法回顾 9

1.2.1 合理成桥状态下的成桥索力确定 9

1.2.2 施工过程张拉索力计算 9

1.2.3 存在的问题 9

1.3 本文项目背景 10

1.3.1 钢箱梁、桥塔施工 12

1.3.2 斜拉索张拉顺序 12

1.3.3 施工监控—索力计算及调整 13

1.4 本文的主要工作 13

第二章 多段索异形塔斜拉桥合理成桥状态计算方法 15

2.1 斜拉桥合理成桥状态 15

2.1.1 定义及确定原则 15

2.1.2 常用确定方法 15

2.2 确定多段索异形塔斜拉桥合理成桥索力的分步算法 18

2.2.1 MIDAS/Civil未知荷载系数功能介绍 18

2.2.2 MIDAS/Civil调索功能介绍 19

2.2.3 分步算法的具体计算流程 19

2.3 基于分步算法的多段索异形塔斜拉桥成桥索力计算实例 20

2.3.1 使用刚性支承连续梁法初定塔梁（斜拉）索张拉力 21

2.3.2 初步求解塔间索张拉力 22

2.3.3 索力调整 25

2.3.4 成桥状态分析 31

2.4 采用其他常见成桥状态确定方法的计算结果比对分析 33

2.4.1 零位移法确定合理成桥索力 33

2.4.2 最小弯曲能法确定合理成桥索力 34

2.4.3 影响矩阵法确定合理成桥索力 36

2.5 小结 41

第三章 斜拉桥施工过程索力计算方法 42

3.1 施工过程索力计算方法概述 42

3.2 基于无应力状态法的索力计算 42

3.2.1 索的无应力长度 43

3.2.2 塔、梁单元的无应力曲率 44

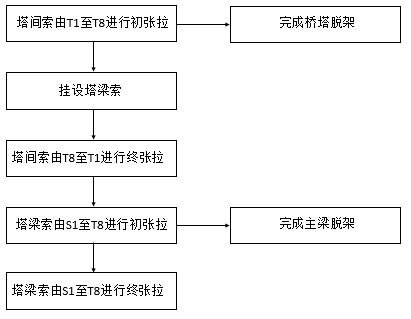
3.2.3 无应力状态法施工阶段索力计算流程 46

第四章 多段索异形塔斜拉桥中间施工状态索力计算 47

4.1 初张拉力的求解 47

4.1.1 塔间索初张拉力计算 47

4.1.2 塔梁（斜拉）索初张拉力计算 47

4.2 终张拉力的求解 47

4.2.1 合理成桥状态无应力长度求解 47

4.2.2 脱架状态无应力长度求解 49

4.2.3 考虑分阶段施工的无应力状态法正装模型 50

4.2.4 锚头拔出量指导施工监控 52

4.3 一次成桥与分阶段正装成桥状态对比 52

4.3.1 成桥索力 53

4.3.2 主梁内力 53

4.4 考虑实际施工中的调索问题 54

4.4.1 临时外荷载 55

4.4.2 张拉顺序调整 56

结论 59

参考文献 60

致谢 61

第一章 绪论

复杂空间索面异形塔斜拉桥发展概况

斜拉桥主要由索塔、主梁、斜拉索组成^[1]。受力时，主梁主要承受弯矩，桥塔受压，拉索受拉，可近似理解为支墩由拉索取代的弹性支承连续梁。

在欧美国家，1617年意大利人FaustusVerantius建造的斜拉铁链桥可视为斜拉桥发展的开端。随着斜拉桥的不断发展，在1907年法国设计的Cassagne桥和1925年修建的Lezardrieux桥已有当代斜拉桥的大体轮廓，但斜拉索仍未达到现代斜拉桥所具有的大索力，斜拉索松弛下垂现象十分明显。在这段时间中，高质量钢材的缺乏以及对斜拉桥理论分析方法的欠缺导致几座斜拉桥相继倒塌，使得工程师们对这种结构体系产生畏忌，在后续一段时间内不愿应用，给斜拉桥设计理论与建造技术的丰富给予了很大限制。

20世纪中期，高强钢材的广泛应用，电脑运算能力的提高，结构理论及桥梁施工工艺的进步，让人们得以重新认识斜拉桥。其中，1938年德国的基辛格工程师提出，为减弱斜拉索在自重作用下的垂度，斜拉索应具有大的索力来提高竖向刚度从而减小梁体变形。该结论成为现代斜拉桥的理论基石。

中国是全球最早拥有吊桥的国家之一，而斜拉桥正是起源于吊索桥^[2]。相对于欧美国家无论是斜拉桥理论研究还是施工建造方面的飞速发展，我国斜拉桥的修建起步较晚，1975年修建的主跨为76米的四川汤溪河桥是我国基于现代斜拉桥理论的首次实践。随着我国基础建设的不停深化，在经济跨径范围内，具有线条纤美、跨越能力强等特点的斜拉桥结构体系在建设数量、造型、跨度上的发展均突飞猛进，湖北鄂东长江大桥等大跨度斜拉桥的成功问世表明中国斜拉桥建设能力紧跟世界发展前沿。

日趋完善的斜拉桥结构分析理论与先进的建造技术使得工程师们的想象力不再被局限，建筑美学成为斜拉桥的重要设计与评价指标^[3]。桥梁除满足日常交通的需求外，发挥一定的城市景观效应已成为设计者、管理者们的共识。复杂空间索面异形塔斜拉桥突破了传统斜拉桥的构造型式，具有的时尚感、轻巧感符合人们对斜拉桥的审美，在城市桥梁建设中逐步得到采用。图1.1至图1.3展示了多种类型的复杂空间索面异形塔斜拉桥。

a) 团泊新桥 b) 英雄大桥

图1.1 有背索曲斜塔斜拉桥

1. 紫气大路立交桥 b) 练江河大桥

图1.2 曲线形桥塔双索面斜拉桥

a) 华阳彩虹桥 b) 东江梨川大桥

图1.3 无背索异形塔斜拉桥

可以发现，复杂空间索面异形塔斜拉桥的出现，让城市桥梁不仅是跨越江河的连接构造物，更成为城市独特的文化印记。表1.1列出了我国近期修建的复杂空间索面异形塔斜拉桥。

表1.1 近期国内部分异形塔斜拉桥

斜拉桥索力计算方法回顾

合理成桥状态下的成桥索力确定

当代斜拉桥绝大部分属于密索结构体系，结构设计计算较为复杂。为推导斜拉桥的合理成桥状态，国内外学者提出了一些计算方法，包括：

（1）指定受力状态或位移状态法^[4]，如刚性支承连续梁法^[4]、零位移法^[4]、内力或应力平衡法^[5]等；

（2）未将索力分布、支墩反力等因素计入考虑，只对目标参数进行优化来调整索力的无约束索力优化法，如：弯曲能最小法^[5]；

（3）在优化目标参数的同时将索力分布等因素计入考虑的有约束索力优化法，如：用索量最小法。

施工过程张拉索力计算

自20世纪60年代至今，国内外不少学者对此进行了研究与探讨，得出了一些重要结论，这里将一些代表性进展简要列出:

20世纪60年代，德国桥梁结构工程专家 F. Leonhard^[6]提出了倒装计算法，也就是现在所说的倒拆法。倒拆法基本思想是将确定的成桥目标状态视为推导的起始点，按施工过程的逆序逐步推导分析，来计算建设过程中各施工阶段结构的内力与位移状态^[7]。

1999年颜东煌、刘光栋^[8]介绍了确定斜拉桥合理施工状态的正装迭代法。该法基本思路为：先假设斜拉索施工张拉力 ，按桥梁正常施工建造顺序建立模型计算出成桥状态，利用最小二乘法原理将该状态与合理成桥状态间不闭合的差值逐渐减小来不断修正索力，直至收敛。Praveen^[9]等设计了空间有限元软件对美国Clark斜拉桥进行了按正常施工顺序正装的仿真计算。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：