摘 要

华科应用电磁所的太赫兹源即将进行升级改造。为了实现改造后储存环的稳定运行，太赫兹源的束流轨道系统必须进行相应改造，以满足储存环的供束要求。束流轨道中的双向校正磁铁因为注入模式改变、老化等原因也需要重新设计，该磁铁要求能同时能提供水平校正和垂直校正的功能。

本文的工作主要是设计并优化电子束流轨道中的双向校正磁铁。磁铁的铁芯为C型，水平的二极场主要是由导线分布决定，垂直的二极场则可通过垫补磁极面来优化。

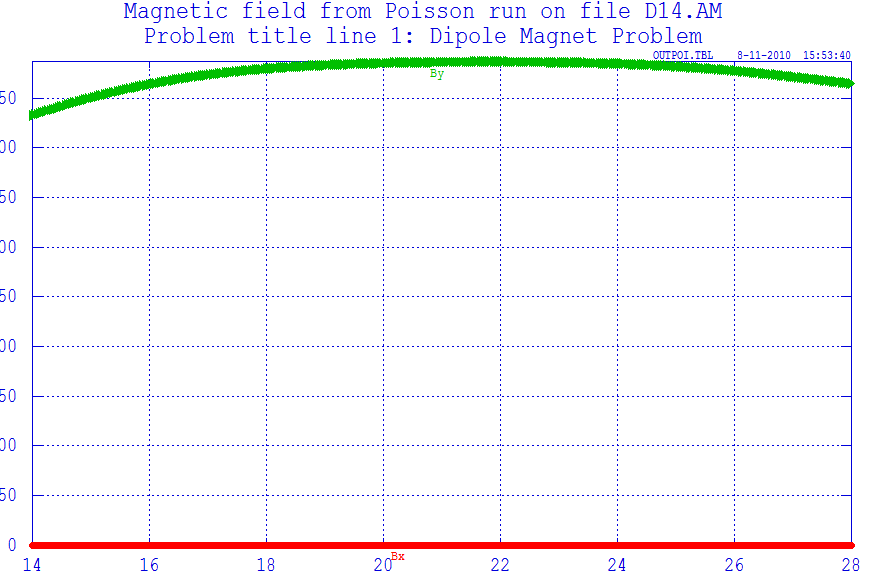
设计过程首先用AutoCAD设计出基本形状，根据磁轭、线圈的各点坐标等用Poisson Superfish建立模型，根据已知条件设置模型的参数、边界等。然后对此进行优化，以达到注入器用的标准。由于两个方向的独立性，水平、垂直二极场可以分别加以优化，前者主要通过修改导线、电流分布，而后者主要通过修剪磁头提高二极磁场品质。本文给出了具体优化过程和最后达到标准的水平、垂直二极场的设计方案。

关键词：电子束流轨道 双向校正 二极铁 磁场

Abstract

The bidirectional correction magnets of injector are designed and optimized in this paper. For the C-type dipole magnet, the horizontal magnetic field distribution is mainly determined by the coil, while the vertical dipole field can be optimized by shimming magnet pole face.

Terahertz source will be upgraded. In order to achieve a stable operation mode of the storage ring, injector must be modified accordingly to meet the beam requirements for the storage ring. Because of the new injection mode, aging problem and other factors, the bidirectional correction magnets of the injector also need to be redesigned. The correctors should provide horizontal and vertical magnetic fields simultaneously.

First, use AutoCAD to create a basic shape. According to the coordinates of the magnetic yoke and the coil we build the model with Poisson Superfish, and set the model parameters under the given constrains, boundary conditions and so on. Then we are to optimize the magnet to meet the requirement. The horizontal and vertical dipole field can be optimized respectively, the former mainly by modifying the coil, (current distribution), while the latter mainly through the cutting of the magnet pole to improve the quality of dipole field. In this paper, the optimization process and the final design plan which meet the standards for both horizontal and vertical fields are given.

Keywords: Electron beam orbit, Bidirectional correction, Dipole, Magnetic field

第一章 绪论

组合功能束流轨道校正磁铁设计

自由电子激光（Free Electron Laser, FEL）是一种以相对论优质电子束为工作媒质，在周期性磁场中与辐射光场相互作用，受到能量和密度调制后，以受激辐射放大的形式产生的相干同步辐射光源，具有波长连续可调，强相干，高功率、高稳定性、可精确控制的脉冲时间结构光源^[1]。产生高品质自由电子激光对电子束流轨道的要求非常高：束流在输运线中的轨道偏差会造成其不能通过四极磁铁的中心，从而会产生额外的二极偏转磁场分量，并且出现残余色散，直接影响电子束流的品质^{[8] [9]}。另外在波荡器元件中，为了使得束流与辐射光场尽量充分的相互作用，要求束流轨道与激光光轴完全重合，这也同样对束流轨道提出高的要求^[2]。

可以实现束流轨道校正的元件主要包括驾驶线圈和二极校正磁铁，其中驾驶线圈只对低能量束流作用效果明显，所以在带电粒子加速器建设中，二极校正磁铁是最常被用到的元件。通常二极磁铁会分为两种类型：分离型和组合型^[8]。分离型通常需要两块磁铁组合使用，每块分别完成水平、垂直方向的轨道校正。这种分离校正铁因为沿纵向占用更多空间，所以在空间位置有局限的情况下，特别是在紧凑加速器上不适用。目前已有的组合功能校正铁是在水平、垂直方向同时可实现轨道校正，一般为框型结构，磁场沿横向分布的均匀性较差^[6]。

针对于此，本课题计划完成一套新型组合功能校正磁铁设计方案，在缩小空间的同时大大提高磁场沿水平面和沿垂直面的均匀性。本论文主要是对这样一块混合型双向校正磁铁做出理论上的设计和优化。

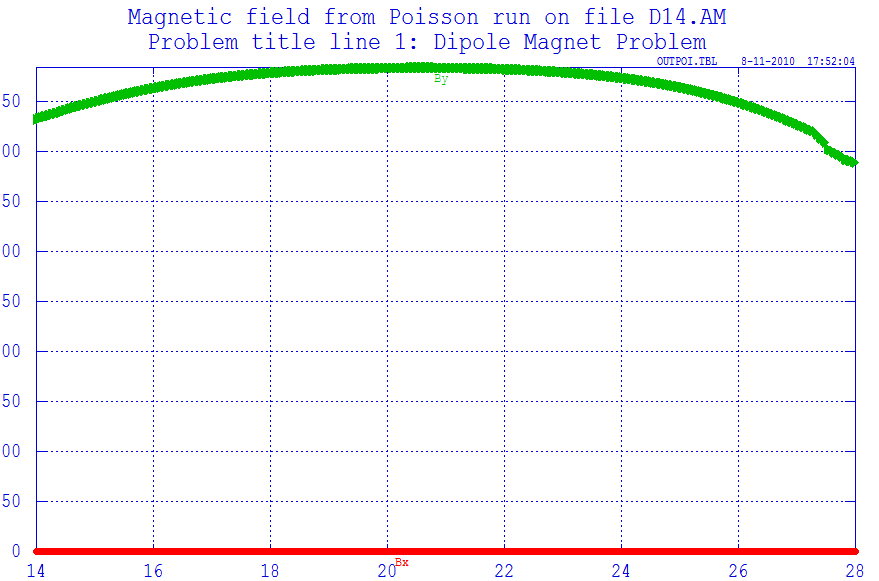
表1.1给出了校正磁铁主要设计参数要求。

表1.1 注入器静态校正磁铁主要设计参数表^[3]

第二章 磁铁设计原理

第一节 磁铁的基本组成、分类和用途

一、基本组成部分

普通的电磁铁主要由磁轭和线圈构成。

磁轭（magnet yoke），通常指本身不生产磁场（磁力线），在磁路中只起磁力线传输的软磁材料，磁轭一般采用导磁率比较高的材料，如软铁等来制造。通过磁轭，我们可以把通电线圈或者永磁体等产生的磁力线按照需要引导到到特定地方，形成磁场。

线圈(coil) ，就是通电导线绕成的线圈，通常有很多匝，根据毕奥萨伐尔定律（Biot-Savart law），电流产生磁场，因此它是常规电磁铁磁场的主要来源。

这两部分缺一不可：只有磁轭不能产生强度可调节的磁场，只有通电线圈，也无法得到特定要求的磁场。因此磁铁设计主要包括的就是这两方面的设计。

二、磁铁的分类和用途

主要的磁铁类型包括：二极铁（dipole） 、四极铁（quadrupole）、六极铁（sextupole），它们产生的磁场分别是均匀、线性分布、二次分布的磁场，各自的作用分别为弯曲、汇聚带电粒子束和提高粒子束的品质^[3]。还有一些特殊用途的磁铁这里就不一一列举了。

下面分别是这三个类型磁铁的示意图，其中±Pole为两磁极，打叉和圈的为线圈，叉为垂直进入纸面，圈反之，红色箭头的为磁力线Flux，也就是磁场的方向，蓝色的为垂直入射带正电的粒子的受力方向。

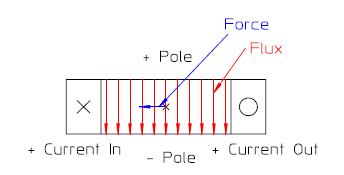
图2.1 二极铁

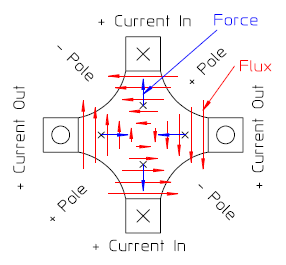
图2.2 四极铁

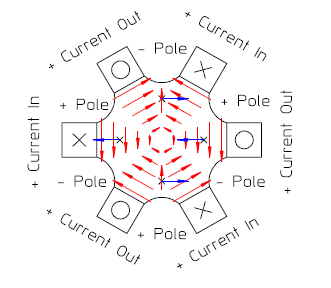
图2.3 六极铁

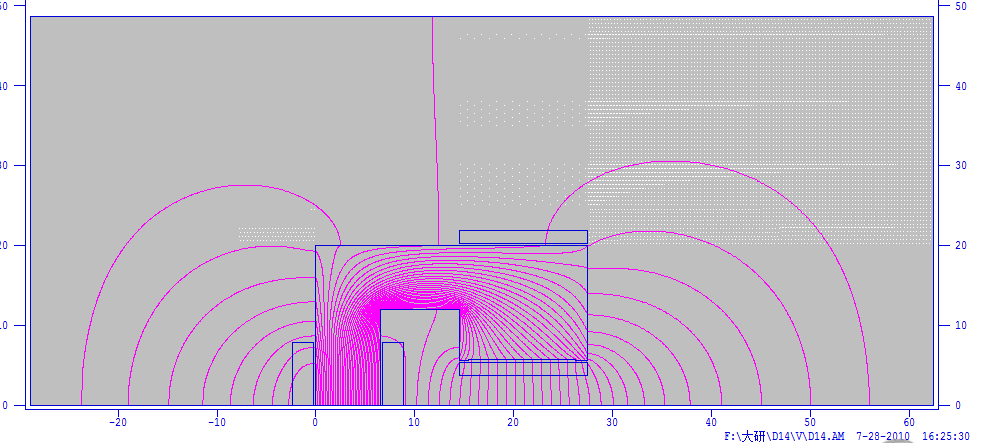
我们要设计的双向校正磁铁属于二极铁的一种，所谓的双向校正就是在一块磁铁上同时实现垂直、水平二极场，同时能对粒子束的垂直、水平方向运动做校正。设计一块在好场区内场分布尽量均匀的校正磁铁是下面我们努力希望达到的目标。

第二节 磁场的计算和相关理论

一、麦克斯韦磁场方程

磁场的计算主要用到的就是麦克斯韦方程组中与磁相关的两个方程，即：

(2.1)

其中第一个方程本质上就是安培环路定律的微分形式，第二个方程的物理意义则是不存在磁单极子。这两个方程，加上完整的边界条件，理论就可以求解磁场。

下面我们主要对这两个方程做一些处理，引入“矢势——A”、“标势——V”和复方程的概念来简化方程的求解。

首先由旋度、散度的一些定理知，梯度场的旋度必为零，而旋度场的散度为零，因此由方程（2-1）、（2-2）知，B可以表示成一个量的旋度或一个量的梯度前者即A矢势，后者为标势V

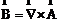
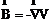
（这里的标势和普通电动力学上定义的标势略有不同，后者的梯度为磁场强度H，而不是磁感应强度B）。

当把上面两恒等式分别代入（2-1）无电流情况、（2-2），则分别有：

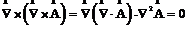(2.2)

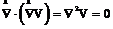(2.3)

其中（2-3）在库伦约束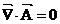（）下，也可化为拉普拉斯方程。

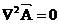接下来我们引入复方程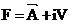,易知F同样满足拉普拉斯方程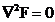。当然这个方程成立的条件是没有电流存在的区域，对于有电流的区域，因为我们主要计算模拟的是二维的磁铁，下面只出一个二维的情况。

把（2-1）展开后有

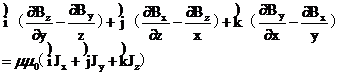
只分析x、y平面上的磁场，则有

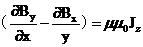
其中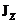是平行于z轴的任意点的电流密度，用F表示上述方程则可以得到

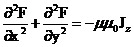
二、方程的求解及磁场相关

1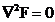）方程的通解

对于复变量F，如果F可以表示成复变量z=x iy的函数，

我们可以得到恒等式：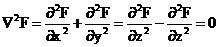

这说明了复变量z的任意函数都是满足拉普拉斯方程的，由此我们可以得到两个特殊形式的解，作为解磁场方程的通解F=A iV 和 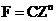，两个方程都可以帮助我们更好的求解或者说理解磁场，各有优劣。

2）与磁场的联系

当我们用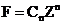来描述“理想多极磁铁”的磁场时，这里的整数n，代表的是磁极个数的一半，比如说n=1,2,3……分别可以描述二极铁、四极铁、六极铁等。当然实际的磁铁不可能是这么理想的，所以还包含了其他高阶小量，这里我们称之为高阶项或者误差项。我们可以很容易想到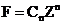，的所有泰勒展开项都是满足拉普拉斯方程的，因此实际的磁场的解我们可以用下面的方程表示^[3]：

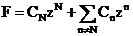
其中N表示基本项，大小为磁极个数一半，也即是理想场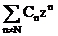，表示磁头本身及由制造加工和装配等误差。当然这里的n也不是任意的，由多极铁的旋转对称性可知有对称约束：

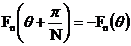
在极坐标下表示上述方程则有

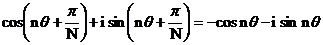
将实部虚部分别相等则很容易可以得到对称约束必须满足：

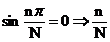= 1, 2, 3, 4, ... , all integers

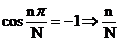= 1, 3, 5, 7, ... , all odd integers

综上n/N必须满足是奇数，即可取的n为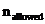：= N (2m 1) ，其中m为任意整数，比如二极铁N=1，则允许的误差项为 = 3, 5, 7, 9, ...

三、方程解与二极铁进一步联系

首先我们将问题简化为理想的二极铁，也就是磁头平行的、无限延伸的线性磁铁。由上面的讨论知，理想二极铁可以用N=1的复方程描述：F = 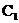z = 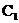(x iy) = A iV。当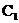是实数的时候将实部虚部分别对等有：

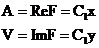
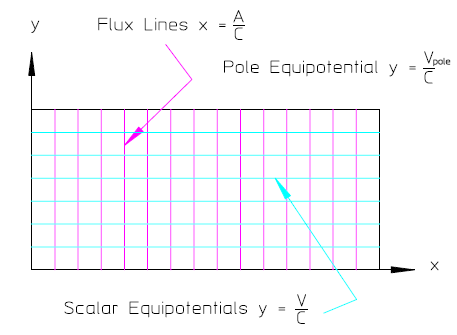
从上面的两个方程易得二极铁的等矢势、等磁标势线分别为垂直x、y坐标轴的直线，这从某种程度上已经刻画了二极铁的磁场特征，如图2-4。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：