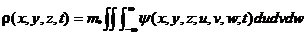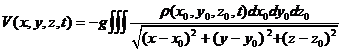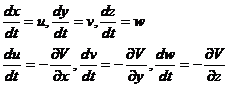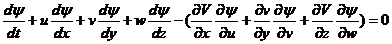星系运动的数学模型及其求解毕业论文
2020-02-14 14:50:29
摘 要
本文主要借助几大物理定律,以及常微分方程,以及扰动理论,对单个行星以及N个行星组成的体系的运动方程进行了模拟,由此推广到星系的运动方程,将其转化为一个常微分方程组的初值问题。论文主要研究了星系的分布,分类,以及星系里单个恒星的运动和N个粒子组成的体系的运动。本文通过扰动理论常微分方程的计算了解了星系的组成以及恒星的运动方程其运动规律,进一步在推导出星系的运动方程,使我们对于天文学,星系运动有了进一步的了解。
关键词:星系运动;动力学;恒星;广义相对论;扰动理论
Abstract
This paper mainly uses several physical laws, as well as ordinary differential equations, and perturbation theory to simulate the equations of motion of a single planet and N planets, thus extending it to the equation of motion of the galaxy and transforming it into a constant differential. The initial value problem of the equations. The paper mainly studies the distribution and classification of galaxies, as well as the motion of a single star in a galaxy and the motion of a system composed of N particles. In this paper, we understand the composition of galaxies and the motion law of stellar motion equations through the calculation of perturbed theoretical ordinary differential equations, and further derive the equations of motion of galaxies, which gives us a better understanding of astronomy and galaxies.
Key Words:Galaxy movement,;dynamics; stellar; general relativity;Disturbance theory
目 录
摘 要 I
Abstract II
第1章 绪论 1
1.1 研究目的 1
1.2 国内外研究现状 1
第2章 星系结构分析导引 3
2.1 支配星系行为的物理定律 3
.2.2 宇宙的构造组元 3
2.3 星系分类 4
2.4 星系的组成 4
2.5 恒星体系的动力学 4
2.6 横越银盘的恒星分布 6
2.7 星系螺旋的密度波理论 9
第3章 行星轨道 11
3.1 开普勒定律 11
3.2万有引力定律 12
3.3 反问题:行星与彗星的轨道 13
3.4根据广义相对论求得的行星轨道 15
3.5 关于方法选择的评论 15
3.6 N个粒子:一个确定性的体系 16
参考文献 18
致谢 20
第1章 绪论
1.1 研究目的
浩瀚的宇宙年龄大约为一百亿年,它大约由一百亿个星系组成,星系便是它的构造组元。这些星系是气体和恒星的一种轮廓分明的集合,他们大体均匀的分布在宇宙中,不过还有一定程度的不均匀性;星系通过相互之间的引力吸引作用形成了一些星团。我们所处的星系-银河系,就是由十七个星系组成的星团中的一员.每个星系约由一百亿个恒星组成,我们的银河系属于最大之列.在星系中还存在大量的气体,就像是一种完全电导体,为了分析星系的运动,我们首先必须把它放在适当的数学位置上,首要的一步就是建立一个理想化的模型
数学模型是用数学符号、数学式子、程序、图形等对实际课题本质属性的抽象而又简洁的刻画,它能解释某些客观现象,或预测未来的发展规律,或为控制某一现象的发展提供某种意义下的最优策略或较好策略。数学模型并非现实问题的直接翻版,它的建立常常既需要人们对现实问题深入细微的观察和分析,又需要人们灵活巧妙地利用各种数学知识。通过建立数学模可以将自然规律简化到一个等式中,随着科学的发展,数学建模已经成为了数学的一个重要方面,我们应当认真去学习和对待。
1.2 国内外研究现状
星系有自转和公转,自转是整个星系绕自身的某根轴在转动,类似地球绕地轴的自转。所以星系自转表现为星系众多恒星绕星系中心的转动,但是恒星的角速度随恒星到星系中心距离的不同而不同。我们称其为叫做较差自转或较差转动。大部分星系都有自转,其中盘状星系(包括旋涡星系和透镜状星系)的转动速度较大,椭圆类星系较小。
除了自转以外,星系还有多种形式的整体运动。星系的运动主要包含着两种成分,一是系统性的退行运动,二是星系的本动。
系统性退行运动比较简单。从宇宙中任一点去看远处的星系,都会发现同一个现象,它们在离自己远去。产生这种现象的原因是宇宙大爆炸引起的空间膨胀,其速度服从哈勃定律,距离越远,退行速度越大。所以我们又诚这种系统性的退行运动为 “哈勃流”。比较近的室女星系团距离为六千两百万光年,退行速度约1200000米/秒;而距离32.6亿光年的长蛇II星系团,退行速度为60 000000米/秒。 相对而言,星系本动则要复杂很多。
星系本动,字面意思便是指单个星系本身的运动,速度因星系而异,具体情况决定于周围星系的引力作用大小。星系的空间分布“毫无章法”,星系本动速度(包括大小和方向)也不一样,即“随机分布”,毫无规律可言。如果在一个区域内有着质量极大的天体系统,比如星系团或者超星系团,那么其巨大的引力作用就会使附近其他星系的本动速度呈现一定的规律性,产生趋向于这个大质量天体系统的运动。所以,仔细分析星系本动的规律,就能够发现这种局域性的大质量天体系统,并能够进一步探究星系本动的其他性质。
1988年,林登贝尔等人分析了400个左右“椭圆星系”的星系本动速度,分析结果表明了星系的本动有着两种趋势:其一是趋向室女星系团中心的运动,其二则是趋向半人马座中某一点的运动。趋向于“室女”中心的运动,是由于“室女”的引力,使得周围星系的运动偏离了哈勃流。而如果朝着半人马座中某一点的运动,就说明那一点一定有一个区域汇聚了大量的物质,或者集合了大量的星系团,即“巨引力源”。巨引力源的距离大约为2亿光年,比“室女”远得多,但它造成的星系本动速度差不多有600000米/秒,而室女星系团引起的星系本动只有将近250000米/秒。
星系团有缓慢自转,表现在团内星系为绕着星系团的中心在转动。但是不同星系在团内的运动速度并非一致,而是有不同之处,这就说明团内星系之间互相有着相对运动。团星系相对运动速度的大小一般用弥散速度作衡量。也就是说,星系团范围越大的话,团星系弥散速度也就会越大;小星系团内星系的弥散速度大约为250000~500000米/秒,而大星系团内星系的弥散速度则可以高达2000000米/秒。
星系团的整体运动,包括哈勃定律的哈勃流运动和团的本动两种运动。哈勃流运动的规律是距离越远,退行速度就会越大,因此对遥远的星系团来说,其退行速度足够大,这个时候来说,团的本动相对于哈勃流来说是次要的,但是对距离比较近的星系团来说,本动速度更加明显,甚至有可能超过哈勃流的速度。
在这里我们只研究星系的“自转”,对于星系的其他运动,只有在我们对星系有着进一步了解之后方可进行进一步的研究。
第2章 星系结构分析导引
我们要指出理论分析是如何能够开始解释星系结构的各个方面的。正如所有自然现象的数学理论一样,我们要求知道:(i)有关的基本物理定律,(ii)所研究体系的特征。
要求(i)可以简短地予以说明,因为要用到的定律就是经典物理学定律。为了满足要求(i),我们要向读者简短地介绍一下宇宙的定量概貌。而后再比较详细地介绍一下能够预言横越银盘的恒星分布的这样一个问题的表述和解答。最后,我们十分粗略地讲一下关于螺旋结构(这是许多星系的一种特征)起因的某些新观念。
2.1 支配星系行为的物理定律
研究星系所用到的基本物理定律就是经典物理学定律:(i)所有经典力学都要遵循的牛顿运动定律以及牛顿万有引力定律;(i)麦克斯韦的电动力学定律以及(n)热力学定律。
要注意的是,以经验为基础的基本定律用得非常少。不过,为了研究某些物理问题,我们经常需要引入新的数学概念.例如,在本节末尾的特例中,仅仅用到牛顿时代的物理定律。但是我们欲要用到诸如相空间以及相空间中的密度这样一些更为近代的数学概念。
现在我们转而概述一下关于我们宇宙的某些事实。应该指出,我们引用的定性与定量的知识乃是几世纪以来大量科学努力的成果。
.2.2 宇宙的构造组元
我们膨胀着的宇宙年龄大约为一百亿年.现时,它大约由一百亿个星系组成,星系便是它的构造组元。这些星系是气体和恒星的一种轮廓分明的集合,它们大体均匀地分布在(看来是浩瀚无垠的)宇宙中.不过还有一定程度的不均匀性:星系通过相互之间的引力吸引作用形成了一些星团。我们所处的星系——银河系。就是由十七个星系组成的星团中的一员。
让我们把银河系的一些特征引述一下,以使读者对于星系的本性有一个总印象。银河系形如一薄盘,在其中心有一个大体是球状的核。(太阳差不多位于银河系的边缘上,离中心约有10000个秒差距)离中心大约15000秒差距的地方,银河系的物质密度变得十分小了。银河系处于旋转之中;在太阳附近的线速度约有250公里/秒。
最近的恒星约有4光年(1.3pc)之遥。对比而言,冥王星的轨道约为40A:U. (2 times; 10-4pc)因而,太阳系好像是单原子气体中的一个原子;,这种气体是相当稀薄的,至少在我们附近是这样。
一秒差距(pc)=3times;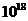 cm.地球绕太阳轨道的半径(称作天文单位A.U.)对于这段距离所长开的角度为一秒(以弧度为单位),因此它约为
cm.地球绕太阳轨道的半径(称作天文单位A.U.)对于这段距离所长开的角度为一秒(以弧度为单位),因此它约为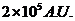 ,一光年约为0.3pc.一个以一公里每秒的速度运动的物体大约经过一百万年才走了一秒差距的距离。
,一光年约为0.3pc.一个以一公里每秒的速度运动的物体大约经过一百万年才走了一秒差距的距离。
2.3 星系分类
根据外貌,可把星系分为下列四类:(i)椭圆形(包括球状)的,(i)正规螺旋状(盘状)的,(i)棒状螺旋的,以及(iv)不规则的。
星系的分类最初仅是根据几何外貌作出的,而详细的研究结果表明:几何特征是与其它物理参数(例如气体含量)有关的。这表明,持续甚久(几百亿年)的星系外貌上的差异是有其动力学基础的。
盘状星系由于要保持其形状而必然处于急速旋转之中。球形星系大概没有净旋转。不同扁度的椭圆形星系具有不同程度的旋转。棒状星系处于匀速旋转之中,但不是绕对称轴转动,由引力维系着的这种旋转系统的经典例子是由数学家雅可比(Jacobi1804—1851)发现的。
由哈勃与德.沃库勒而斯绘制德星系分类方案德总图将星系分类为椭圆形 ;正规螺旋S0,Sa,Sb,Sc,Sd;以及有闩螺旋SBO,SBa,SBb,SBc,SBd。
2.4 星系的组成
每个星系约由一百亿个恒星(更精确地说,由109—1011个恒星)组成。我们的银河系属于最大之列。太阳是一个普通的恒星,年龄大约为五十亿年。大质量恒星,例如质量40倍于太阳的恒星,极其明亮,它们很快会耗尽其核燃料,因而必定形成得较晚(比方说是在过一千万年这段期间内).太阳的演化是十分缓慢的;它的核能再过一百亿年也消耗不完。
在星系中还存在着大量的气体——在不规则星系中可达百分之二十以上,在Sc螺旋星系中要少些,而在Sa螺旋星系中则减少到百分之一或二,在巨大的椭圆星系中几乎没有了。我们银河系的气体含量约为百分之三到四。
在这样大的尺度上,气体就像是一种完全电导体,虽则仅有少量气体电离,并且按地球范围的标准来衡量,导电性也很小。由星际气体中的电流产生的宇宙磁场仅有几个微高斯(即10-6高斯,高斯是磁场的cgs单位)。
宇宙线粒子与各种波长的电磁辐射(从alpha;射线到X射线,再到可见光,直至无线电波)弥漫于星际空间。这些对于气体和磁场都可能有影响。因而我们采用'星际介质'这一名词来描述整个体系,它与恒星体系之间仅有微弱的相互作用。的确,恒星与气体之间的主要动力学相互作用是引力作用。
2.5 恒星体系的动力学
为了分析星系的结构(例如解释螺旋结构),我们首先必须把它放在适当的数学位置上。怎样着手处理如此复杂的一个体系呢?
早已说过,首要的一步是建立一个理想化的模型。只有把有关的经验事实以及支配我们所研究的体系的普遍规律搞清楚之后,才能着手完成这一步。
表2.1 银河系的能量密度
|
源由 |
能量密度(单位:尔格/ |
|
总辐射(星光) |
0.7 |
|
气体的湍流运动 |
0.5 |
|
星系旋转的总能量 |
1300 |
|
宇宙线 |
1 |
|
磁场(高斯) |
4 |
可以看到下列各种成分对能量密度的贡献是依次递减的:(i)恒星体系(占了特别突出的比例),(i)气体,(i)磁场,以及(iv)宇宙线粒子和其它形式的辐射。这样,我们就应该从能量最大的部分,即恒星体系的动力学的表述开始。现在就来讲述这种表述。
恒星之间距离的数量级是它们的半径的106-107倍(这一距离是恒星最外层行星半径的许多倍),相距如此遥远的这样一组恒星的集合,可以看作是一组受到引力吸引的质点集。这样就可以按照牛顿运动定律和万有引力定律写出支配它们行为的动力学方程组,在第二章中,我们将仔细讨论这种方程组。然而,用这种方法描写星系显然是不恰当的,因为我们不能指望去追踪百亿个恒星中的每一个恒星的运动。我们必须以某种集体方式,也就是以统计描述方式去研究它们。
为简单起见,我们考虑恒星质量相同的理想情况,(关于这一理想化的正确性的讨论必须留给这方面的专著去完成,)既然一个恒星的运动是由它的位置和速度决定的,因而我们考虑在一给定的位置和速度范围中的恒星数目。为了作出精确的数学表述,我们把位置坐标和速度坐标合在一起,引进六维(x,y,z;u,v,w)的相空间。我们这样来定义时刻t在这一相空间中的恒星的相空间数密度或分布函数中(x,y,z;u,v,w;t),使得Psi;(x,y,z;u,v,w;t)dxdydzdudvdw给出了这样的一些恒星的数目。它们的三维空间坐标分别处在(x, x dx), (y, y dy), (z,z dz)这一范围中,而三个速度分量落在(u,u du), (v, v dv),(w, w dw)这一范围中。这样,分布函数少就给出了任何时刻恒星体系的一个完备描述D:为了描写动力学过程,我们必须考虑这一分布函数随着时间的变化。恒星质量密度rho;(x, y, z, t)可用分布函数Psi;表示出:
|
|
(2.1) |
式中m✳是单个恒星的质量。这一方程仅仅表示为了得出总的质量密度,我们必须把具有各种速度的所有恒量的质量加起来。
每一恒星是在所有其它恒星的总引力场中运动着。除去恒星之间的切近碰撞'之外,一个恒星的单独运动基本上只受到物质的弥漫分布(其密度由(2.1)式给出)所产生的引力场的作用。这种引力场由引力势V(x,y,z,t)的负梯度给出,V(x,y,z,t)与密度P之间的关系式为
|
|
(2.2) |
此处G是万有引力常数(G=6. 7times;10-8cgs单位)。这样,每个恒星的运动方程可以写作
|
|
(2.3) |
进而再考虑到质量守恒以及假定不存在碰撞,便可断言:相空间某一部分中的质量增加必定是由穿过该部分的边界的物质流所引起的。所证明的那样,这意味着:
|
|
(2.4) |
注意,引力场▽V是通过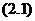 与
与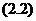 式与分布函数Psi;联系起来的,因而
式与分布函数Psi;联系起来的,因而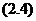 式括号中的各项是
式括号中的各项是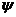 的二次型;也就是说,如果以
的二次型;也就是说,如果以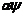 (
(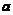 为常数)代替
为常数)代替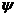 ,那么相当于在这些项前面乘以一个因子
,那么相当于在这些项前面乘以一个因子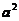 。因此
。因此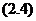 式是一个非线性方程。
式是一个非线性方程。
单个恒星运动所遵循的方程(2.3),与所有恒星集体运动所遵循的方程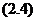 之间存在着密切的关系。用偏微分方程理论的语言来说,方程组(2.3)是描述方程
之间存在着密切的关系。用偏微分方程理论的语言来说,方程组(2.3)是描述方程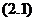 的特征曲线的。
的特征曲线的。
倘若知道了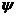 ,由于利用
,由于利用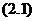 与
与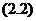 式可以算出引力势,因而根据
式可以算出引力势,因而根据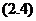 式便可求出任何时刻的
式便可求出任何时刻的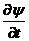 .所以从发展的眼光来看,一旦给定了某一时刻的
.所以从发展的眼光来看,一旦给定了某一时刻的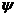 ,可以认为
,可以认为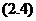 式充分
式充分
描述了其后的恒星体系.要想对上述说法从数学理论上给予证明,就要困难多了,尤其是当我们提出像稳定性这类问题的时候。所谓稳定性,指的是如果稍微改变一下最初给定的分布函数,那么解的变化是否仍是微小的?这类问题往往不能严格解决;但是应用数学家仍然必须把他的工作进行下去,当然,除了诉诸于他所希望的但不是现存的数学定理之外,他还要作另外的仔细考虑,从而对于他的工作是有意义的这一点他必须有相当把握。
2.6 横越银盘的恒星分布
作为应用上述方程组的一个比较简单但是真实的例子,让我们考虑横越银盘的恒星分布,这一问题至今尚未完全解决,在我们银河系太阳的附近,看来存在着'物质失落'。'下面给出的解,通常是作为检验观察结果的主要基础的。
银盘的半径达10千秒差距,但其厚度仅有600秒差距。因而在极好的近似程度上,我们可以把银河系在垂直于银盘方向上的变化看作是十分局部的。我们把这一垂直方向取作轴,把盘心取为z=0。那么在稳态情况下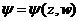 ,而(4)式变为
,而(4)式变为
|
|
|
可以证明,位势V(z)满足泊松微分方程