基于灰狼优化算法的车间调度研究毕业论文
2020-02-15 23:32:56
摘 要
制造业在国家经济发展中占了重要比重,生产调度是制造系统的基础,而置换流水车间调度问题是很多现实车间中调度问题的简化模型。已经证明,超过三台机器的置换流水车间调度问题是NP-hard问题,难以用运筹学方法精确求解。近些年来,元启发式算法已经成为学者们研究的热点。灰狼优化算法是一种新的元启发式算法,在连续函数优化方面,和其他著名的元启发式算法相比具备竞争优势。
本文采用一种改进的灰狼优化算法对置换流水车间调度问题进行研究求解,目标为最大完工时间最小化,采用基于随机键编码的升序排列ROV规则实现连续位置向量到离散调度方案的转换,采用一种将收敛因子非线性改变的策略,对算法的全局搜索和局部搜索能力进行合理地协调,通过对十个基准测试案例的实验,将结果与基本灰狼优化算法和粒子群算法进行比较,证明了算法的有效性。
关键词:灰狼优化算法;置换流水车间调度问题;非线性收敛因子;随机键编码;最大完工时间
Abstract
Manufacturing industry plays an important part in national economic development. Production scheduling is the basis of manufacturing system, and permutation flow-shop scheduling problem is a simplified model of scheduling problems in many real workshops. It has been proved that the permutation flow-shop scheduling problem with more than three machines is a NP-hard problem, which is difficult to be solved accurately by operational research method. In recent years, meta-heuristic algorithm has become a hot topic for scholars. Grey Wolf optimization algorithm is a new meta-heuristic algorithm. Compared with other famous meta-heuristic algorithms, it has competitive advantages in continuous function optimization.
In this paper, an improved grey wolf optimization algorithm is used to solve the permutation flow-shop scheduling problem. The objective is to minimize the maximum completion time(makespan). The upgraded ROV rule based on random key coding is used to transform the continuous position vector to the discrete scheduling scheme. A strategy of changing the convergence factor nonlinearly is adopted to reasonably coordinate the global search and local search ability of the algorithm. Through the experiments of ten benchmark test cases, the results are compared with the basic grey wolf optimization algorithm and particle swarm optimization algorithm, which proves the effectiveness of the algorithm.
Key Words:Grey Wolf Optimization;Permutation Flow-Shop Scheduling Problem;Non-linear Convergence Factor;Random Key Coding;Makespan
目 录
第1章 绪论 1
1.1 研究目的及意义 1
1.2 国内外研究现状 1
1.2.1 置换流水车间调度问题 1
1.2.2 灰狼优化算法 2
1.3 研究内容和论文结构 4
1.3.1 研究内容 4
1.3.2 论文结构 4
第2章 理论基础 5
2.1 置换流水车间调度问题描述 5
2.2 灰狼优化算法的介绍 6
2.2.1 基本思想 6
2.2.2 数学模型 7
第3章 算法设计 12
3.1 编码方式 12
3.2 种群初始化 12
3.3 适应度函数 13
3.4 非线性收敛因子 13
3.5 个体位置更新 14
3.6 算法步骤 14
第4章 实验与分析 15
4.1 实验参数设置 15
4.2 实验结果分析 15
第5章 结论与展望 19
5.1 结论 19
5.2 展望 19
参考文献 20
附录 Matlab代码 22
致 谢 34
第1章 绪论
1.1 研究目的及意义
制造业是国民经济的支柱,对国家经济的发展起着关键的作用。现代科学技术和经济全球化的发展,给企业既带来了机会,又带来了挑战。生产规模日益扩大,产品多样性和复杂性逐渐提高,市场竞争也愈加激烈,所以,对制造企业的生产计划管理和控制提出了更高的要求。生产调度作为制造企业生产计划管理和控制的关键环节,正扮演着越来越重要的角色。
生产调度决定着企业的生产能力,一直是生产制造领域中最重要、最受关注的问题之一,是为了实现最佳生产目标而优化制造资源配置的问题。生产调度是指在满足一些等式或不等式的约束条件下将工件分配至合适的机器上,确定每台机器上的工件加工序列和加工开始时间,目的是实现某些指标最优化。它是一种复杂的组合优化问题,生产调度问题中大部分是NP-hard 问题,采用传统的算法求解比较困难,因而采用新的智能算法求解该类问题具有重要的理论和实际价值。
置换流水车间调度问题(Permutation Flow-shop Scheduling Problem,PFSP)是研究最多的一类生产调度问题之一,它主要描述为n个工件在m台机器上进行加工,每个工件在各台机器上的加工顺序相同且每台机器上的工件加工顺序也相同。很多现实中的生产调度问题都可简化为PFSP模型。置换流水车间调度问题在实际生产制造中广泛应用,尤其是大批量生产方式的制造企业,对它的优化可提高制造资源利用率和企业综合效益。同时,三台机器以上的置换流水车间调度问题已经被证明是一个NP完全问题,没有精确算法能够在有限时间内求解。因此,该问题非常有研究价值。
灰狼优化算法(Grey Wolf Optimizer,GWO)是澳大利亚学者Mirjalili等人在2014年提出来的一种新的基于自然界灰狼的社会等级和狩猎机制的群体智能优化算法。它在编程方面比较容易实现、设置需要调整的参数少、收敛速度快。在函数优化方面,已经证明,GWO比其他著名的元启发式算法(如差分进化算法和粒子群优化算法(Particle Swarm Optimization,PSO))具有竞争优势[1]。
本文拟将灰狼优化算法应用于求解置换流水车间调度问题,通过标准测试案例的仿真实验,验证算法的有效性。
1.2 国内外研究现状
1.2.1 置换流水车间调度问题
二十世纪五十年代,Johnson第一次提出了两台机器的置换流水车间调度问题,引起了广泛关注和研究,学者们提出了很多的算法。一般有三类求解方法:(1)精确方法,即运筹学方法,如枚举法、割平面法、动态规划法、分支定界法等,但这类方法只能用于求解小规模的问题,难以在有限时间内求得大规模问题的最优解。(2)启发式方法,如Johnson、Palmer、Gupta、NEH、CDS等,启发式方法虽然能很快求得问题的解,然而一般求得的解质量较差,是局部最优解。(3)元启发式方法,近些年来,计算机技术飞速发展,也在很大程度上促进了人工智能技术的发展,研究者们提出了许多元启发式算法,如遗传算法、禁忌搜索算法、模拟退火算法、蚁群优化算法、粒子群优化算法、人工蜂群算法、差分进化算法等求解调度问题。这些方法处理约束比较简单,对目标函数的限制少,可求得较满意的解,可应用于各种复杂调度问题,目前已成为最流行的方法[2]。
Anurag等人[3]针对多目标PFSP,提出了基于帕累托最优块的分布估计算法,采用双变量概率模型,提高了种群的多样性。Suash Deb等人[4]提出了一种基于犀牛自然行为的元启发式搜索算法,即犀牛搜索算法,对PFSP进行了实现。黄霞等人[5]提出了一种改进的混沌杂草优化算法,求解最大完工时间,总流程时间和总延迟时间最小化的多目标PFSP问题,用灰熵关联度适应值分配策略和多目标进化策略,提升算法的性能。张素君等人[6]提出了一种混合离散人工蜂群算法来求解PFSP问题,将离散蜂群算法与差分进化、变邻域搜索以及模拟退火的概率突跳机制相结合,提高算法的性能。刘勇等人[7]构建了一种求解PFSP的中心引力优化算法,采用Halton低偏差序列初始化种群,运用两位置交换排序法,防止算法陷入局部最优。汤可宗等人[8]提出了一种求解PFSP的多策略粒子群优化方法,采用多样性评价策略、全局最优粒子选择策略、集合变异方式提高算法的性能。王柏琳等人[9]提出一种协同进化遗传算法求解工件可拒绝的有限等待PFSP,将染色体编码分为两个子集,采用协同进化策略依次进化子集种群,提出基于记忆的动态概率设计方法,提高算法的性能。
从上述介绍可以看出,学者们对PFSP的研究求解可以分为两类,一类是采用一些策略对一种智能算法本身进行改进,一类是将一种智能算法与其他算法相结合,这样可以综合不同算法的优点,提出性能更好的混合算法。未来新的元启发式算法不断出现,可将它们应用于求解PFSP,也可以探索不同算法之间的组合,提出新的混合算法来求解PFSP。
1.2.2 灰狼优化算法
2014年,Mirjalili等人[1]首次提出了灰狼优化算法,它是一种新的元启发式算法,模仿自然界灰狼的社会等级和狩猎行为,实现狩猎的三个步骤:追踪猎物、包围猎物和攻击猎物。该算法以29个著名的测试函数为基准,通过与粒子群优化算法、引力搜索算法、差分进化算法、进化规划和进化策略的比较研究,表明了GWO算法的结果很有竞争力。文章中还用GWO算法求解了三个经典的工程问题,拉伸/压缩弹簧、焊接梁以及压力容器设计。
目前,GWO算法在很多领域得到了广泛的应用,如经济负荷调度和表面波分析等。Moumita Pradhan等人[10]将GWO用于经济负荷调度的最优运行策略,该问题考虑了发电机的非线性特性,如斜坡速度限制、阀点不连续性和禁止的操作区,GWO在寻找最优解时,不需要任何关于目标函数梯度的信息,通过在四个测试系统上测试,结果证实了GWO的潜力和有效性。Xianhai Song等人[11]以灰狼为灵感,提出一种新颖而强大的表面波反演方案,称为灰狼优化器,实现了寻找、包围、攻击三个主要步骤,对表面波进行参数估计,提出的策略以无噪音、噪音和现场数据为基准,测试结果表明GWO在勘探和开发之间表现出良好的平衡。
灰狼优化算法在车间调度领域也有很多应用:Komaki等人[12]采用GWO来解决考虑作业发布时间的两阶段装配车间调度问题。Lu等人[13]针对焊接车间的实际调度案例,为优化生产效率和机器负载,提出了一种多目标离散GWO,采用两段式编码方式,通过减少机器负载实现机器负载最小化。Tianhua Jiang等人[14]针对作业车间和柔性作业车间调度问题提出了一种离散GWO算法,在该算法中,基于交叉操作设计了搜索算子,使算法直接在离散域工作,为了保持种群多样性,避免过早收敛,引入了一种自适应变异方法,此外,还采用了一种变邻域搜索方法,进一步增强了搜索效果。吕新桥等人[15]提出混合GWO算法求解PFSP,采用基于随机键编码的LOV规则进行编码,保证解的可行性,采用局部搜索加快算法的收敛,通过标准测试集的仿真实验,和基本GWO算法、GA算法比较,验证了算法的有效性。姜天华[16]提出一种混合GWO算法求解柔性作业车间调度问题,采用两段式编码方法,用启发式规则初始化种群,用一种变邻域搜索方法,提高算法的收敛能力,通过交叉和变异增强算法的全局搜索能力。姚远远等人[17]提出一种改进的混合GWO算法求解作业车间调度问题,进行进化种群动态操作,移除种群中适应度差的个体,提高整个狼群的适应度,用反向学习策略初始化种群,提高种群的多样性,对目前种群最好的灰狼个体进行变异操作,避免算法早熟收敛,仿真结果表明所提算法可以有效跳出局部最优。姜天华[18]提出了一种改进的GWO算法求解以低碳为目标的柔性作业车间调度问题,采用机器分配和工序排序两段式编码,并分别进行种群初始化,将收敛因子非线性调整,采用加权重系数的个体位置更新公式,并结合了局部搜索,改善了算法的局部搜索能力。
虽然GWO算法应用到了很多领域,但它还是有一些缺陷,如求解精度低、收敛速度慢,学者们提出了很多改善措施。王敏等人[19]采用反向学习策略来初始化灰狼种群,以提高算法的全局搜索速度,提出一种非线性变化的收敛因子,来平衡算法的全局和局部搜索能力,对目前最好的灰狼个体进行多样性变异,防止算法陷入局部最优。郭振洲等人[20]提出了非线性收敛因子策略,对算法的全局和局部搜索能力进行平衡,并引入动态权重策略,让算法更快收敛。龙文等人[21]采用混沌进行种群初始化,提高算法的全局搜索速度,修改位置更新方式,加强算法的全局探索,采用非线性调整收敛因子策略,来将算法的探索和开发能力协调好。
未来对GWO算法的改进和将其应用于更复杂的车间调度问题可进一步加深研究。
1.3研究内容和论文结构
1.3.1 研究内容
本文采用一种改进的灰狼优化算法来求解置换流水车间调度问题,采用基于随机键编码的ROV规则实现连续位置向量到离散调度方案的转换,引入一种非线性收敛因子,以此平衡算法的全局搜索和局部搜索能力,通过在十个标准测试案例上的仿真实验,将结果与标准GWO算法和PSO算法进行比较,证明文中算法的有效性。
1.3.2 论文结构
本文主要分为五章:
第一章是绪论。对论文的研究目的及意义进行论述,对置换流水车间调度问题和灰狼优化算法的国内外研究现状进行简要分析,并介绍研究内容和论文结构。
第二章是理论基础。包括置换流水车间调度的问题描述和基本灰狼优化算法的介绍。
第三章是算法设计。包括对灰狼优化算法的编码、初始化、适应度函数、收敛因子、更新操作的设计。
第四章是实验与分析。主要是采用MATLAB编程,用十个标准测试实例对改进GWO算法进行测试,并与标准GWO算法和PSO算法进行对比。
第五章是结论与展望。对本文主要研究内容做出总结,并展望未来的研究方向。
第2章 理论基础
2.1 置换流水车间调度问题描述
置换流水车间调度问题是一个典型的离散组合优化问题,可以描述为:车间里有m台机器和n个工件,一个工件包含m道工序,每道工序在不同的机器上进行加工。每个工件以相同的顺序经过m台机器进行加工,而且每台机器上的工件加工顺序也相同。
这个问题有一些重要的条件:
- 工件是独立的,可以在零时刻进行加工。
- 一旦一个工件在某台机器上开始加工,它就不能被中断或抢占。
- 工件的加工允许等待。
- 不考虑机器故障等因素。
- 每个工件在每台机器上的加工时间是固定已知的。
- 每台机器在任意时刻至多只能加工一个工件,每个工件在任意时刻至多只能被一台机器加工。
最大完工时间是指最后一个工件在最后一台机器上的完工时间。问题的目标是求每台机器上的工件最优加工顺序,使得最大完工时间最小[15]。
PFSP的数学模型如下:问题的一个可行解是n个工件的置换序列,设π={π1,π2,…,πn}是一个工件调度解,πi表示在机器的第i个位置上进行加工的工件。工件 πi在第k台机器上的加工时间是固定已知的,设为p(πi,k)(i=1,2,…,n;k=1,2,…,m)。C(πi,k)表示工件 πi在第k台机器上的完工时间,所以建立数学模型如下:
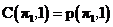 (2.1)
(2.1)
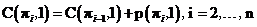 (2.2)
(2.2)
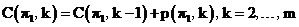 (2.3)
(2.3)




