基于EEMD的桥梁挠度分离研究毕业论文
2020-02-17 00:36:59
摘 要
桥梁挠度是桥梁安全评估的关键因素,反应了桥梁的整体特性,影响着桥梁的稳定性能、美观程度及安全性能。影响桥梁挠度的因素有很多,除了桥梁自重、混凝土收缩徐变等恒载以外,还包括车辆冲击荷载以及外界环境(如风,地震,环境温度)产生的其他荷载。准确分离复杂因素的影响,求出各因素单项贡献值的作用,是评估桥梁安全性能的重要前提。
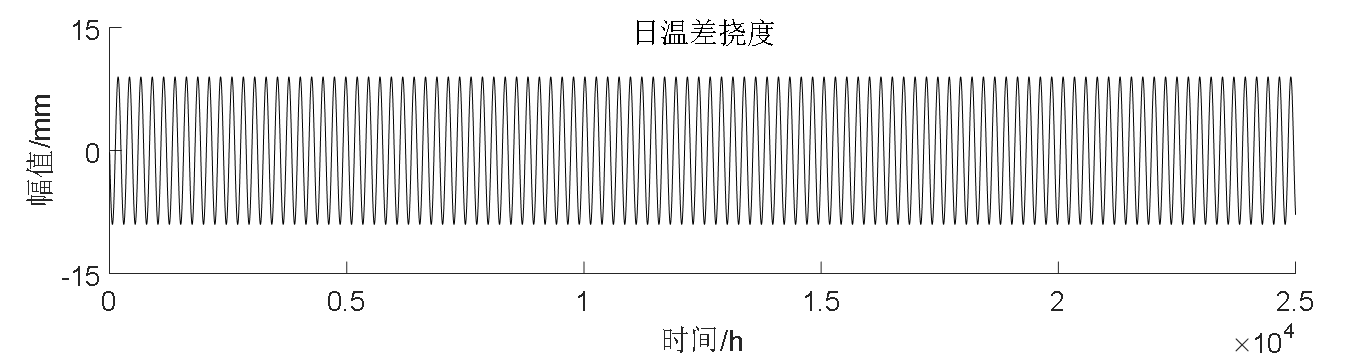
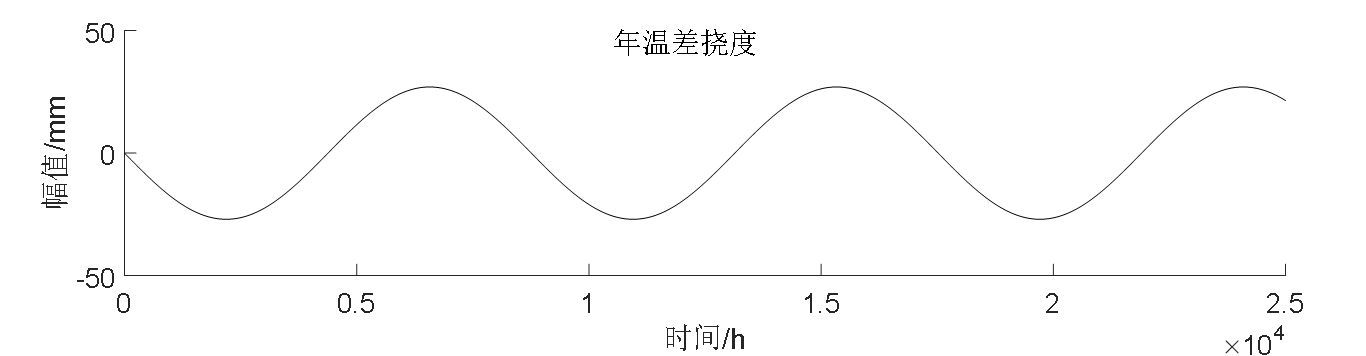
首先,根据不同影响因素具有时间多尺度的特性,可以将不同成分引起的挠度进行分离,从而得到单项因素的量值贡献。其中,活载挠度是动态的,温度挠度的变化频率较小,混凝土收缩徐变引起的挠度变化接近于0。了解了不同因素的时间特性差异之后,便可从信号处理的角度对不同挠度成分进行分离,得到不同时间尺度的作用效应。
其次,对于车辆荷载等高频信号,可采用滤波算法进行分离。对于温度挠度、混凝土收缩徐变挠度等低频信号,传统的信号处理方式难以分离,本文提出了集合经验模态分解与独立成分分析相结合的算法,更精确地分离出不同成分的挠度响应。其中,集合经验模态分解(EEMD)是传统经验模态分解(EMD)的改进算法,分离效果更好,精度更高。独立成分分析(ICA)则解决了EEMD端点效应太过明显的缺点。
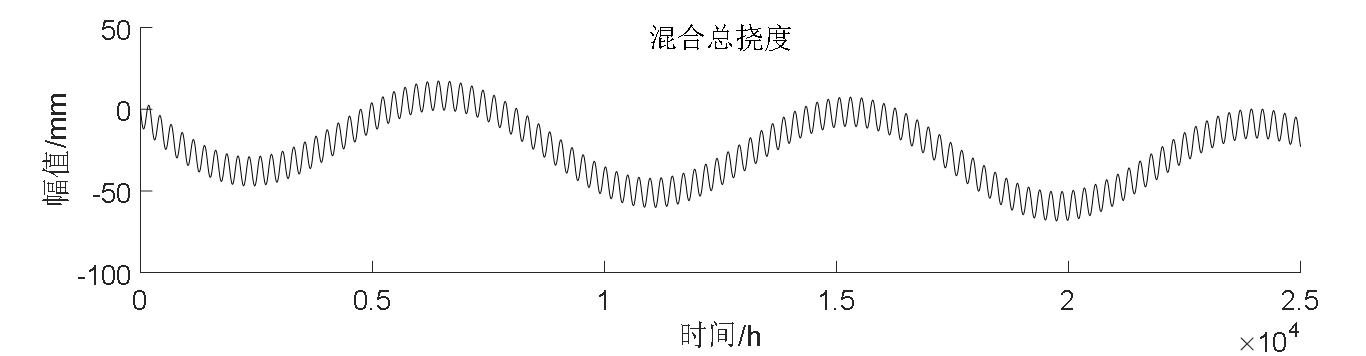
最后,本文通过对总挠度信号的仿真模拟,验证了该方法的可行性。对桥梁施加单项荷载,获得相应的模拟信号,将单项模拟信号进行混合叠加,再经过集合经验模态分解和独立成分分析对单通道混合信号进行分离,分离结果与源信号进行比对发现,两者的相关系数达到0.9以上,说明了分离方法的可行性和准确性。
关键词:集合经验模态分解;独立成分分析;桥梁挠度;改进的PCA
ABSTRACT
Bridge deflection is a key factor in bridge safety assessment, which reflects the overall characteristics of the bridge and affects the stability, aesthetics and safety of the bridge. There are many factors affecting the deflection of the bridge, in addition to the dead weight of the bridge, concrete shrinkage and creep and other constant load, including vehicle impact load and the external environment (such as wind, earthquake, environmental temperature) generated by other load. It is an important prerequisite to accurately separate the influence of complex factors and calculate the contribution value of each factor.
First of all, according to the time-scale characteristics of different influencing factors, the deflection caused by different components can be separated, so as to obtain the magnitude contribution of single factor. Among them, the live load deflection is dynamic, the change frequency of temperature deflection is small, and the deflection change caused by concrete shrinkage and creep is close to 0. After understanding the difference of time characteristics of different factors, the components of different deflection can be separated from the perspective of signal processing to obtain the effect of different time scales.
The second, high frequency signals such as vehicle load can be separated by filtering algorithm. Traditional signal processing methods are difficult to separate low-frequency signals such as temperature deflection and concrete shrinkage and creep. EEMD is an improved traditional EMD algorithm with better separation effect and higher precision. Independent component analysis (ICA) solves the disadvantage that EEMD endpoint effect is too obvious.
The last, the feasibility of this method is verified by the simulation of the total deflection signal. Bridge applying single load to the background, to get the corresponding analog signal, mix single analog signal superposition, through the collection of empirical mode decomposition and independent component analysis was carried out on the single channel of mixed signal separation, compares with the source signal separation results found that the correlation coefficient reaches 0.9 above, the separation method is feasible and accurate.
Keywords: collective empirical modal decomposition; Independent component analysis; Bridge deflection; The improved PCA
目录
第一章 绪论 1
1.1 研究背景及意义 1
1.1.1大跨斜拉桥特点与发展 1
1.1.2大跨斜拉桥挠度问题研究 1
1.2 桥梁挠度信号的分离研究 2
1.2.1 桥梁挠度信号分离研究现状 2
1.2.2 挠度组分分析 3
1.2.3 温度挠度分离方法研究 3
1.基于统计回归的方法 3
2.基于EMD和ICA的方法 3
1.3 本文主要研究内容 3
第二章 基于信号分离的理论分析 5
2.1 EMD基本理论及其改进算法 5
2.1.1 EMD算法的基本理论 5
1.EMD的应用范围 5
2.EMD算法的主要问题 5
2.1.2 EEMD算法及其步骤 5
1.EEMD基本理论 5
2.EEMD分解步骤 6
2.2 改进的主成分分析PCA 6
2.2.1 改进的PCA基本原理 6
2.2.2 改进的PCA算法流程 6
1.改进的PCA算法流程 7
2.二次降维 7
2.3 独立分量分析ICA 7
2.3.1 独立分量分析的定义 7
2.3.2 FastICA算法 8
2.4 本章小结 9
第三章 桥梁挠度分析计算 11
3.1 Midas/civil模型 11
3.1.1 Midas/civil软件介绍 11
3.1.2 斜拉桥模型模态分析 11
3.1.3 温度荷载挠度及建模 13
1.温度荷载挠度的成因 13
2.温度挠度建模 13
3.2 仿真总挠度的分离 15
3.2.1 基于ICA算法的低频挠度信号分离 15
3.2.2 分离结果评价 18
3.3 本章小结 19
第四章 桥梁实测挠度信号分离 20
4.1 活载挠度测取 20
4.1.1 工程概况 20
4.1.2 项目概述及监测方法 20
4.2 实测数据处理 21
4.2.1 二月份实测数据处理 21
1.桥梁主跨跨中挠度数据处理 21
2.桥梁边跨跨中挠度数据处理 26
4.2.2 七月份、十月份实测数据处理 27
4.2.3 一年内实测数据处理 28
4.3 数据结果分析及评价 29
4.4 本章小结 30
第五章 结论与展望 31
5.1 结论 31
5.2 展望 31
参考文献 32
致谢 34
第一章 绪论
1.1 研究背景及意义
1.1.1大跨斜拉桥特点与发展
斜拉桥又被称作斜张桥,是依靠拉索将桥身拉在桥塔上的一种桥梁,主要由斜拉索、索塔、主梁等结构构成。我国斜拉桥发展水平和修建数量位于世界前列,据不完全统计,我国1986~1990五年间造成斜拉桥33座,1991~1995五年间建成43座,1996~2000五年间建成33座。目前世界上建成的最大跨径的斜拉桥为我国的苏通长江大桥,主跨径为1088米,于2008年4月2日试通车。图1-1为苏通大桥实景。

图1-1 苏通大桥实景
大跨斜拉桥以其优美的造型、出众的跨越能力、合理的受力性能等特点,越来越广泛的被用于桥梁建设中。然而在便利交通的同时,斜拉桥也存在着一定的安全隐患,近年来桥梁垮塌事故频发,造成了巨大经济损失以及人员伤亡。因此,桥梁安全问题是一重大课题。
1.1.2大跨斜拉桥挠度问题研究
桥在恒、活荷载等多种因素综合作用下,梁的轴线会沿纵向发生偏转弯曲,形成一条在纵对称面内的曲线,我们将其称之为梁的挠曲线,横截面形心与轴线的垂直距离即为线位移。挠度的大小与构件截面的尺寸、构件材料性能、荷载大小等因素有关。挠度变化值是反应桥梁安全状态最直观的参数之一,在桥梁安全监测中起着至关重要的作用。
调查表明,大跨斜拉桥在运营实践过程中,主跨跨中普遍存在不同程度的下挠问题,其下挠值远远超出设计范围,且稳定性无法得到保证。这种问题的存在,不仅影响了桥梁的美观性,更重要的是造成桥梁的安全性能降低,给桥面行车带来不便。因此,桥梁挠度的研究是当今保证桥梁安全性能的重要课题。
通常情况下,实际测得的桥梁挠度是各种因素综合影响下的总响应。将各种因素所产生的作用效果分离,能直观地体现不同要素对桥梁挠度的影响效果。因此,将挠度分类是十分必要的。
为了明确大跨斜拉桥下挠机理,建立长期挠度预测机制,从而确保桥梁的安全性和稳定性,不少学者对桥梁下挠成因及各因素对桥梁下挠的影响程度做出过定性分析。2010年,曹诗荣对桥梁挠度变形的检测方法进行了分析指出了桥梁挠度监测的重要性;同年,徐金锋提出了利用二次样条有限元计算桥梁挠度的新方法,能够更加精确有效的对桥梁挠度进行分析计算;2016年,郭宁、王宪军、刘华等人早期混凝土对大跨连续刚构桥挠度的影响,通过有限元模拟,分析了各工况下桥梁挠度的变化量。
在实际工程中,由于混凝土收缩徐变的影响因素较为复杂,且没有统一的计算方式;不同桥梁所处的环境温度有所差别,具有较大的不确定性。因此,在建模过程中,无法精确模拟桥梁的实际情况,想要准确得到单项因素对桥梁挠度的作用效果并不容易。
随着桥梁监测技术的发展,利用信号处理挠度数据的方法应运而生。简单来说,是对从监测系统中获取的挠度数据进行研究,利用信号处理来建立一种数学模型,分离出离散时间信号,从而得到不同时间尺度的作用效应。这种方法有效解决了原方法的缺陷,大大提高了计算结果的精确性,能够更好地应用于桥梁监测,提高了桥梁的稳定性和安全性。
1.2 桥梁挠度信号的分离研究
1.2.1 桥梁挠度信号分离研究现状
随着信号分离技术的发展,针对桥梁挠度的应用也越来越广泛,国内学者对此做了不少研究。2013年,刘夏平、杨红等人利用奇异值分解的方法对桥梁挠度的信号分离进行了研究,有效分离出挠度检测信号的各种效应值;同年,陈晓冬针对大跨径PC梁桥的挠度特性进行了研究,得到了桥梁在车辆荷载、温度作用下的单因素贡献值;2015年,刘夏平、杨红等人提出了基于EMD的盲源分离方法,对桥梁挠度的信号分离研究提供了新思路,更加有效地了解桥梁特性。
1.2.2 挠度组分分析
桥梁挠度是各种影响因素在综合作用下产生的,可表述为:
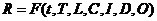 (1-1)
(1-1)
式中,R为挠度响应总信号,是外部因素作用下挠度效应的总和;t为时间作用;T表示热效应;L为车辆荷载;C为混凝土收缩徐变所产生的影响;I为结构损伤作用;D为结构恒荷载作用;O表示其他作用。各因素都对桥梁挠度产生不同影响,但它们产生的响应在形式上并不耦合,信号组分是相互独立的,因而可以进行信号分离。
1.2.3 温度挠度分离方法研究
温度挠度与长期挠度在一定程度上有相近甚至重叠的部分,因此要将这两者分离,采用传统的滤波方式无法实现。温度效应分离有以下两种常见方法:
1.基于统计回归的方法
统计回归是指观测值不完全呈函数关系,但又有一定数量关系的现象,回归分析能够更好了解和预测观测值。基于统计回归的方法是利用统计分析建立回归方程,预测温度对桥梁产生的挠度变化,从而分离温度挠度的一种方法。典型的统计回归方法有人工神经网络方法,最小二乘支持向量机(LS-SVM)等。
2.基于EMD和ICA的方法
经验模态分解(EMD)方法是一种针对非线性、非平稳信号的自适应信号分解算法,这种算法不同于傅里叶分解与小波分解方法,它依据数据自身的时间尺度特征来进行信号分解。因此,该方法在提出后便得到了学术界的广泛关注与研究,并逐渐应用于不同的工程领域。独立成分分析(ICA)是一种函数,将多维信号分离开来,并通过构造函数和优化算法来进行求解。将这两种算法结合起来,便能够分离出混合信号中各因素对挠度的不同响应,完成温度、荷载等对桥梁挠度的作用效果的研究。
1.3 本文主要研究内容
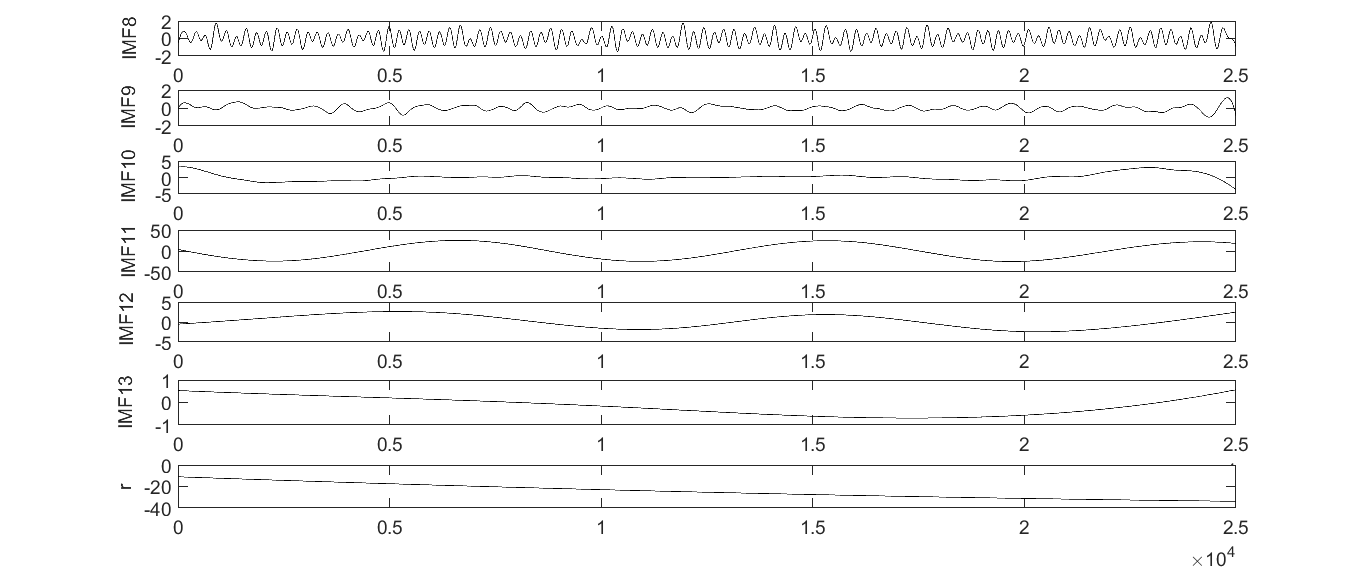
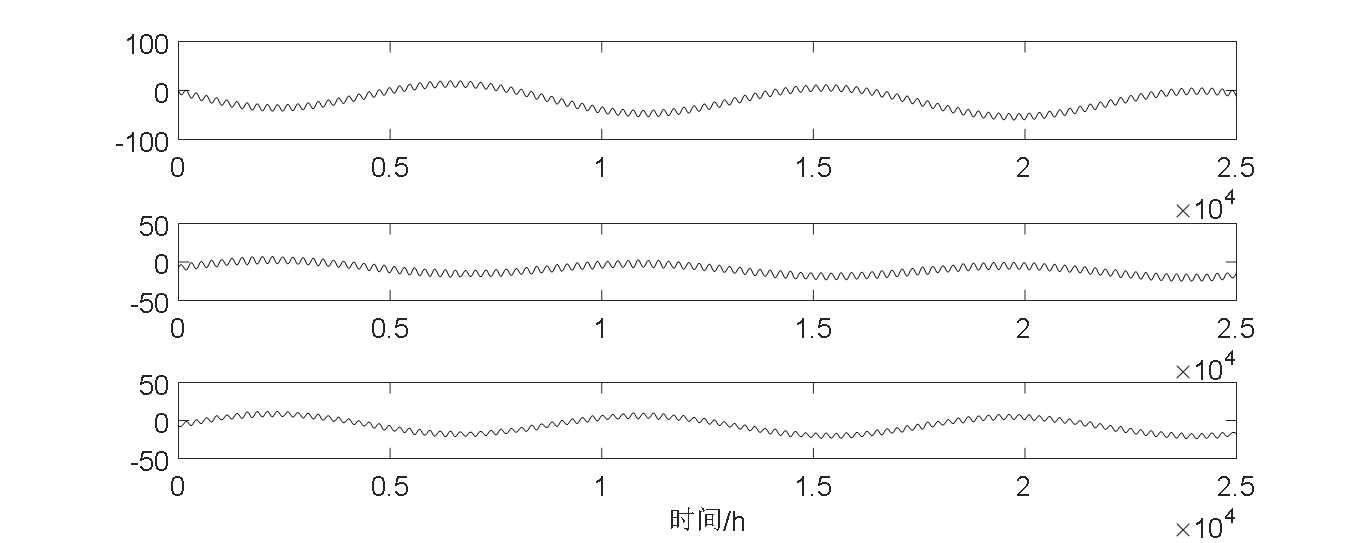
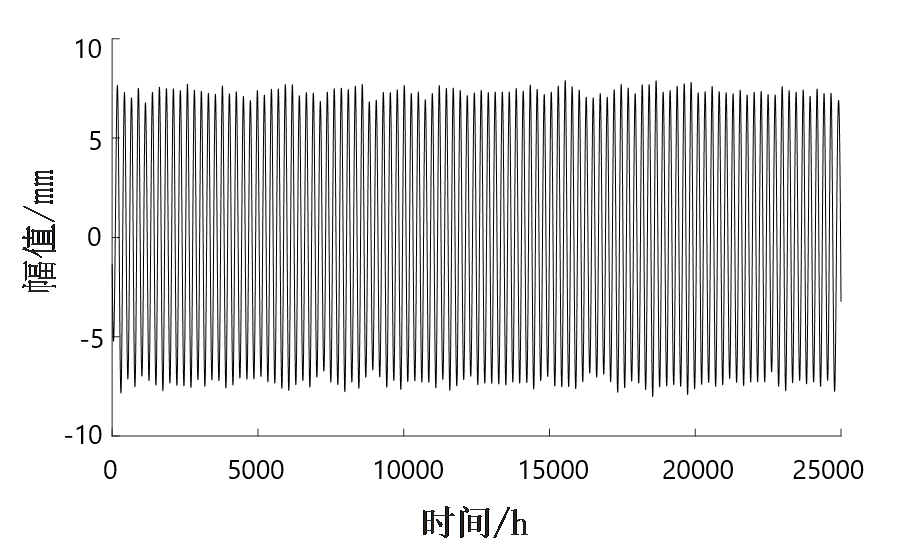
本论文提出一种基于集合经验模态分解法(Ensemble Empirical Mode Decomposition,EEMD)与盲源分离相结合的一种算法,并以桥梁挠度模拟信号为研究对象,收集实测的挠度数据,运用集合经验模态分解及独立分量分析进行分离试验研究,从而精确得到分离桥梁挠度成分中不同时间尺度的作用效应。
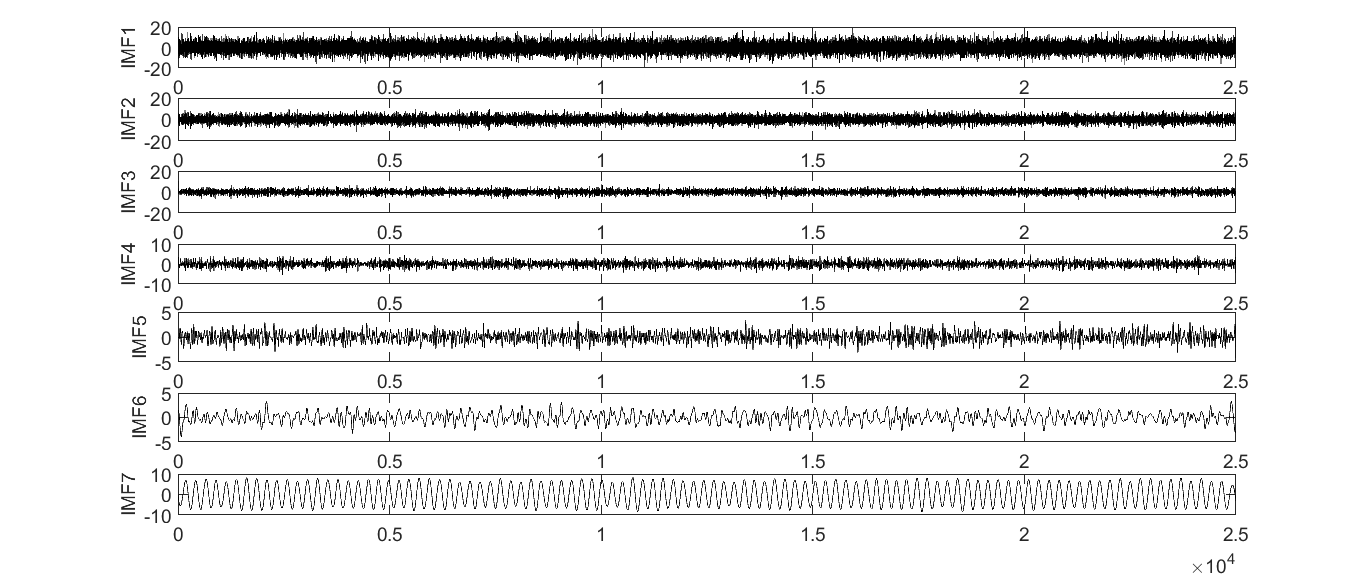
首先,向通过监测所得到的混合挠度信号中加入白噪声,然后对混入白噪声的信号进行经验模态分解(Empirical Mode Decomposition,EMD)。针对这一步骤进行多次循环,最后将得到的多个模态函数分量进行集合平均消除先前加入的白噪声进而得到最终的模态函数分量。利用占优特征值法对源信号进行源数估计,然后采用K-L散度的判别法识别并剔除虚假的IMF分量,并构造出盲源分离算法模型,最后采用经典的盲源分离算法对所得信号进行分离。这对于桥梁的健康监测和避免重大安全事故的发生具有重要理论意义与工程应用价值。
第二章 基于信号分离的理论分析
2.1 EMD基本理论及其改进算法
2.1.1 EMD算法的基本理论
EMD是将复杂的信号函数分解成有限的本征模态函数(Intrinsic Mode Function,IMF)之和的一种算法。通过对IMF分量进行变换,得到非平稳信号完整的时频分布。这种方法具有很高的频率分辨率和自适应性,为信号处理的研究提供了新思路。
1.EMD的应用范围
EMD可用于滤波和去噪过程,由于它具有类似小波的二进滤波器特性,能够克服小波变换使用中的选择小波基难等问题,因而能够方便有效地对非平稳信号进行滤波和去噪。
EMD在信号检测中也是必不可少的,合适的信号处理方法是信号处理与检测的关键。在信号处理过程中,信号的相位或频率时而会发生突变,对于如干扰噪声引起的突变较小的信号,我们很难通过时间位移曲线进行辨识。EMD方法能够分解各模态的瞬时频率,从而定位频率发生突变的时刻,这种方法在结构破坏检测中也是行之有效的。
2.EMD算法的主要问题
EMD能够将多成分的信号自适应地分解为一组本征模态函数(IMF)以及一个残余量,用公式可表示为:
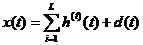 (2-1)
(2-1)
虽然EMD算法具有很好的自适应性,但由于算法是基于经验而成的,所以不可避免会存在一定的问题。首先,EMD算法的分析过程对于噪声干扰非常敏感,这种影响会显著反映在各个IMF分量中,使得IMF分量的波形受到一定程度的影响。此外,由于噪声的存在,信号形态变化的规律性难以保证,这便导致EMD分解之后的分量个数有所增加。
经验模态分解过程中产生的另一个重要问题便是模态混叠,由于瞬间信号的存在,导致同一个IMF分量信息中包含了不止一种信号特征,从而使得分解后的IMF信号的频率、波形相互混叠,增加了提取有效信息的难度。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: