摘 要

随着高速铁路事业的飞速发展，为了适应铁路跨线和特殊地形的需要，我国在高铁线路中建造了大量的简支梁桥，针对高速列车通过简支梁桥的车桥耦合振动问题引起人们的关注。针对这个问题，众多的专家学者采用不同的数值仿真模拟方法开展了相关研究，耦合时变和分离迭代方法是其中的两种方法。虽然以往有针对两种方法各自的研究，但是对于两种方法的对比研究还比较少，因此本文在实现两种方法计算的基础上，对两种方法在计算稳定性、计算精度、计算效率等方面进行了对比研究。受自然科学基金项目（51678576）的支持，本文的主要研究如下：

基于赫兹轮轨分离的接触模型，分别建立列车-轨道-桥梁垂向耦合系统耦合时变方法和分离迭代方法的系统动力方程。

根据谱半径理论讨论分离迭代法稳定收敛的条件。谱半径分析的结果表明：对于轮轨分离模型而言，时间积分步长越小，分离迭代法的计算结果越容易收敛。代入通用简支梁桥的计算参数，得出分离迭代法收敛的边界条件是时间积分步长必须小于3.7/10000 s。

以8节车辆编组的CRH2高速列车通过5跨预应力简支箱梁桥为工程算例，对比验证耦合时变方法和分离迭代方法的计算结果，两种方法的计算结果吻合度较高，达到了计算精度的要求。并研究了耦合时变方法不同动力响应指标对于时间积分步长的敏感程度。结果表明：钢轨加速度对于积分步长最敏感，钢轨位移、车体振动加速度、桥梁位移以及轮轨垂向力等响应指标对时间积分步长的变化不敏感，在1ms的时间积分步长下即可得到相对准确的结果，因此在不关注钢轨加速度的情况下采用较小的积分步长可以提高计算效率，其中时间积分步长采用1ms的计算效率是0.1ms的10倍左右。

关键词：车桥耦合系统；耦合时变；分离迭代；时间步长

Abstract

With the rapid development of the high-speed railway industry, in order to meet the needs of railway crossing lines and special terrain, China has built a large number of simply supported beam bridges in the high-speed railway line. Aiming at the problem of high-speed train passing over simply supported beam bridges, many experts and scholars have carried out related research using different numerical simulation methods. Coupling time-varying and separation iterative methods are two of them. Although there have been studies on the two methods in the past, there are few comparative studies on the two methods. Therefore, based on the calculation of the two methods, the paper studies the computational stability, computational accuracy and computational efficiency of the two methods. Supported by the Natural Science Foundation project (51678576), the main results of this paper are as follows:

Based on the contact model of Hertz wheel-rail separation, the system dynamic equations of the train-orbit-bridge vertical coupling system coupling time-varying method and the separation iterative method are established respectively.

The conditions of the stable convergence calculation of the separation iterative method are discussed according to the spectral radius theory. The results of spectral radius analysis show that for the wheel-rail separation model, the smaller the time integration step, the easier the separation iteration method converges. Substituting the calculation parameters, the boundary condition for the convergence iterative method is obtained. The time integration step must be less than 3.7/10000s.

The CRH2 high-speed train with 8 vehicles is passed through the 5-span simply supported beam bridge as an engineering example. The calculation results of the coupled time-varying method and the separation iterative method are compared and verified. The calculation results have a high degree of agreement and meet the requirements of calculation accuracy. The sensitivity of different dynamic response indicators of coupled time-varying methods to time integration step size is studied. The results show that the rail acceleration is the most sensitive to the integral step size. The response of the rail displacement, the vibration acceleration of the vehicle body, the displacement of the bridge and the vertical force of the wheel and rail are not sensitive to the change of the time integral step, and can be obtained under the integral step of 1ms. A relatively accurate result is obtained, so that the calculation efficiency can be improved by using a smaller integration step without paying attention to the acceleration of the rail, wherein the calculation time of the time integration step is about 10 times that of 0.1 ms.

Key Words: vehicle-bridge coupling system; coupling time variation; separation iteration; time step

目 录

第1章 绪论 1

1.1 研究背景 1

1.2 研究意义 1

1.3 车桥耦合振动问题 2

1.4 车桥耦合振动研究现状 4

1.4.1 车辆模型的发展与现状 7

1.4.2 运动方程的发展与现状 8

1.4.3 外激励源的发展与现状 9

1.5 主要研究内容 13

第2章 列车-轨道-桥梁耦合动力学模型 14

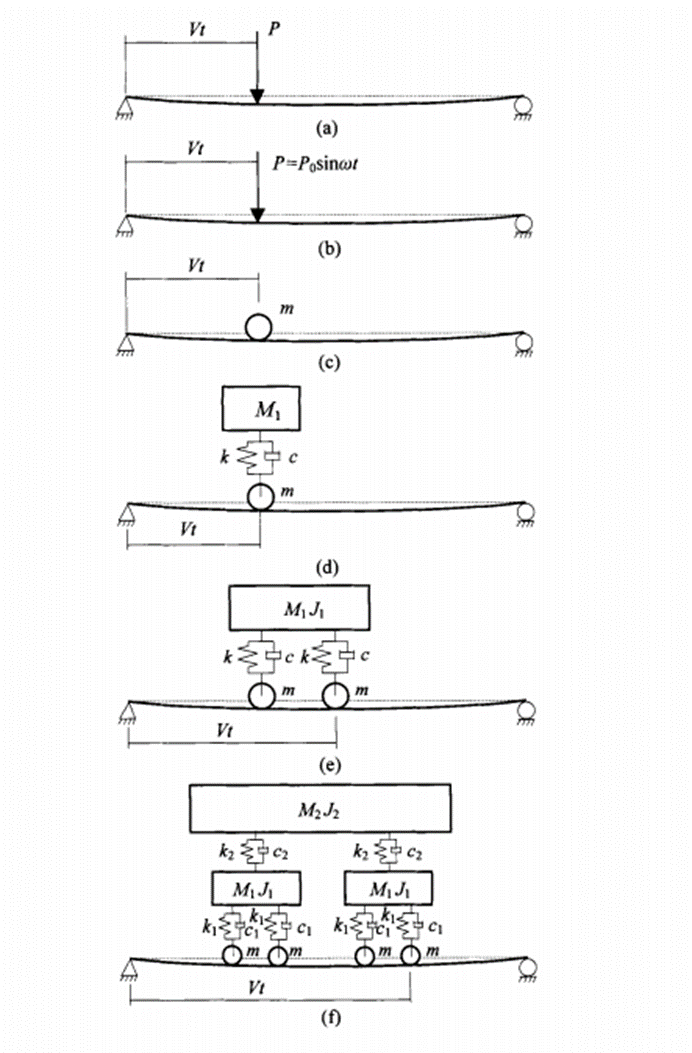
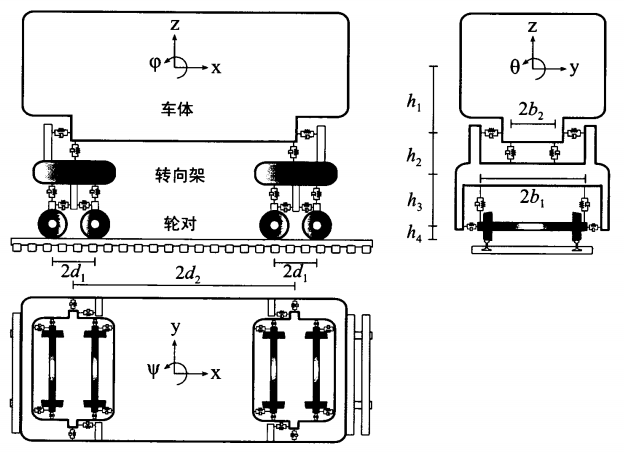
2.1 车辆动力学模型 14

2.2 轨道-桥梁动力学模型 18

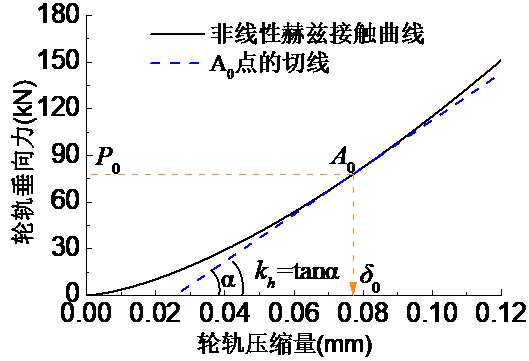
2.3 轮轨接触关系 18

2.4 本章小结 20

第3章 耦合时变方法 21

3.1 耦合时变动力方程的建立 21

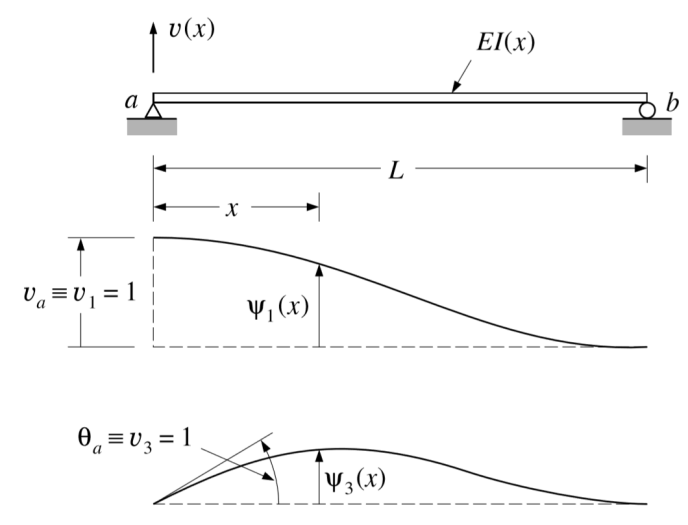
3.1.1 平面梁单元有限元分析 21

3.1.2 轮轨刚度耦合 23

3.1.3 耦合系统荷载向量 25

3.2 Newmark-β积分方法 25

3.3 移动簧上质量模型计算 27

3.4 本章小结 30

第4章 分离迭代法 32

4.1 迭代法动力方程建立 32

4.2 移动簧上质量模型分析 33

4.3 移动簧上质量模型求解 33

4.4 本章小结 36

第5章 时间积分步长对积分稳定性与计算精度的影响 38

5.1 时间积分步长 38

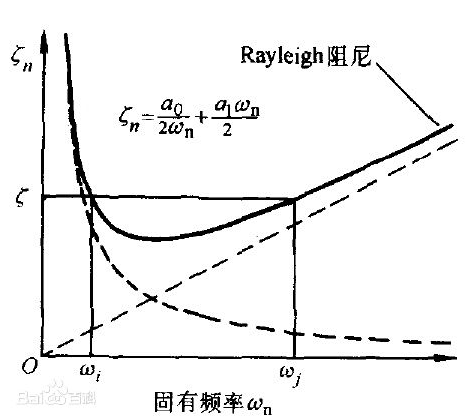
5.2 谱半径分析迭代稳定性 39

5.3 本章小结 43

第6章 桥简支梁工程算例 45

6.1 工程简介 45

6.2 计算参数 45

6.2.1 列车参数 45

6.2.2 桥梁参数 46

6.2.3 计算工况 51

6.3 两种方法的计算结果 52

6.4 不同响应指标积分敏感性分析 58

6.5 本章小结 61

第7章 结论与展望 63

7.1 结论与成果 63

7.2 展望 64

参考文献 66

致 谢 70

绪论

研究背景

幅员辽阔、人口众多是我国的基本国情，建立横跨东西和纵越南北的交通网络势在必行。高速铁路因为其长距离运输速度快、全封闭行车安全性高、舒适环保噪音小等特点，非常适合我国的基本国情和对交通运输的要求。因此高速铁路网的发展在我国有着广泛的应用前景。

正因为高速铁路具有以上的优点，高速铁路对于构筑物的工程要求更为严格。从工程技术的角度出发，高铁选线比公路选线的要求更为严格，例如轨道必须有更高的平顺性，线路必须有更大的转弯半径和更小的纵坡度等参数，这就必然要求在高铁线路中桥梁的比重会明显增大。再从经济发展的角度出发，高速铁路必须穿过人口流动量大、经济发达的地区，只有这样才能带动人口流动与经济流动，发挥高速铁路在经济发展中的纽带作用。但是这些经济发达的地区既有城市规划已经完成，公路、水、电、天然气等线路管网等一系列的人工构筑物牵一发而动全身，因此为了跨越已有的人工构筑物，高架桥梁是必然的选择。

基于上面的跨线要求，我国高架线路的比例与国外相比明显更高。并且目前国内建造的高铁桥梁大部分为预应力简支箱梁桥的形式。因此高速列车通过简支梁桥的车桥耦合振动问题引起人们的关注。

不同速度下的列车会对桥梁产生激励，使桥梁产生振动，这时必须保证桥梁的动力响应不能过大，特别是不能产生共振现象，也就是在车过桥的过程中必须保证桥梁结构的安全性。必须控制桥梁的挠度保证轨道的平顺性，避免因为轨道的不平顺导致列车脱轨，也就是在车过桥的过程中必须保证列车行驶的安全性。在对工程问题进行分析时安全是第一要务，但是随着人们对于更高品质生活的追求，旅途的舒适性也成为人们选择出行方式的重要考虑因素，而列车车体加速度与人们乘车的舒适性密切相关。车体加速度成为人们乘车舒适性的重要评价指标之一。桥梁结构的安全性、列车行驶的安全性、乘车的舒适性三大问题也就是列车-轨道-桥梁耦合振动问题的内涵。车桥耦合振动问题

研究意义

通过以往的研究发现：耦合时变方法和分离迭代方法是求解列车-轨道-桥梁耦合系统的两种数值模拟方法，但是使用两种方法求解系统响应的过程中存在一定的问题。耦合时变方法的计算时间比较长，特别是随着桥梁规模的增大，计算效率问题尤为明显。分离迭代方法在计算中可能会出现计算发散的现象，使得计算结果失真等问题。

当在列车-轨道-桥梁模型深度确定的情况下，不同的数值分析方法在计算的精度、效率和稳定性方法有明显的差异，分离迭代方法与耦合时变方法作为求解车桥耦合振动问题的两种方法因为计算理论的差异从而导致其在实际求解过程中的差异。

在过去针对列车-轨道-桥梁耦合振动的分析中虽然采用了耦合时变方法和分离迭代方法进行求解，但是只是针对两种方法中的一种方法进行研究，针对两种方法的比较研究还比较少。因此本文在实施两种方法求解耦合系统的基础上，进行两种理论方法的比较研究，分析两种方法在计算效率、计算精度和稳定性等方面的不同，为以后的研究提供依据。

车桥耦合振动问题

列车经过各种类型的桥梁对于桥梁来说,列车荷载作为一种外部荷载激励作用在桥梁上，会引起桥梁的振动，使桥梁产生动力响应。桥梁产生的动力响应通过轨道传给列车，反过来影响到列车的振动，这就是列车-轨道-桥梁耦合作用。历史上发生了多起高速列车事故，带来了巨大的生命财产损失。下面通过几组图片来引出车桥耦合振动问题。

2005年日本新干线在尼崎市段发生了严重的列车脱轨事件，事故一共造成107人死亡，400多人受伤的灾难性后果。事故原因是驾驶员为了准点到达而没有在弯道减速导致列车脱轨。

图1.1 日本新干线列车脱轨

2011年“KTX山川”高速列车从釜山出发，因线路的信号系统问题，在将到达光明站的时候，发生了列车脱轨的事故，造成了严重的人员伤亡和财产损失。事故原因也是列车未减速导致列车脱轨，由此可见行车安全的重要性。事故照片见图1.2

图1.2 韩国高铁脱轨事故

1998年德国ICE城际高速列车，列车脱轨并撞击桥梁的桥墩导致桥梁坍塌。这是高速铁路上最惨烈的一起事故，一共造成了101人死亡、88人重伤的严重后果。

图1.3 德国ICE列车脱轨事故

从以上的事故可以看出，列车行驶的安全性是车桥耦合振动最主要的问题，随着列车的提速，行车安全性的保证措施必须更为严格。同时桥梁的安全性也是车桥耦合振动的主要问题之一，因为惯性力的参与，桥梁分析的力学问题由单纯的静力学问题转化为动力学问题，在力学原理上变得更为复杂，求解也变得困难。随着人们生活水平的提高，乘车舒适性成为人们出行选择交通方式的重要考虑，因此乘车舒适性也是车桥耦合振动问题的内涵之一。

车桥耦合振动研究现状

欧洲最早开展列车与桥梁间相互作用的相关研究。1825年英国在斯托克顿和达灵顿之间建成了世界上第一条铁路，车桥耦合振动问题也随之产生。但是那时候由于研究方法和研究手段的限制，人们对于车桥耦合振动的研究还处于假设和经验判断为主的阶段，这时候对于车过桥引起的桥梁响应主要有着两种假设：第一种假设认为列车在通过桥梁的过程中，除了列车的重力之外会对桥梁产生一个附加的冲击力，因为附加冲击力的存在，动力作用下桥梁的动挠度会大于静力作用下桥梁的静挠度。第二种假设认为列车在通过桥梁的过程中，因为列车的高速运动和桥梁刚度的存在，桥梁的响应滞后于动荷载作用的时间，也就是当桥梁还没有出现响应的时候列车已经通过桥梁，在这种情况下，动力作用下的动挠度小于静力作用下的静挠度。为了验证各自的假设，外国的学者首先针对铁路桥梁动力学问题开展了相关研究^{[1, 2]}。

十九世纪中期，Wills^[3]针对一座因为动力作用而倒塌的桥梁进行了研究，探究了桥梁倒塌的原因，分析了该桥梁在动力作用下的响应问题，并提交了关于列车作用引起桥梁动力响应的报告。在这份报告中，他认为桥梁倒塌的原因是列车过桥时引起桥梁的动力响应超过了桥梁的承受能力。在此基础上，他将列车过桥的实际模型抽象成圆球过桥的物理模型，但是此模型中的球和桥都没有考虑质量，也没有得出较精确的数学解。Stokes^[4]在Wills建立的物理模型的基础上，建立了数学模型，并利用级数的方法求解该数学模型，得到了比较精确的数学解。

二十世纪初，Kolousk^[5]认为列车对于桥梁的激励主要是通过轮对产生的，随着每一个轮对上桥，都会对桥梁产生一次激励。而每节车厢每个轮对之间的距离是固定，每节车厢的轮对激励都是一个周期，所以把列车模型抽象成具有周期性特点的移动单个力。在此基础上分析了连续梁、钢桥梁、拱桥三种桥梁模型，应用振型叠加的思想求解桥梁的竖向动力响应。美国对于车桥动力问题的研究手段主要是通过大量的试验得出海量的数据，在这些数据的基础上进行统计分析，得出了一些有益的结论：桥梁发生共振的条件是车轮转动的频率与桥梁自振的基础频率接近；列车作用下引起桥梁的动力响应的主要原因是车轮的冲击力。同时美国在列车过桥的分析报告中也首次提出了冲击系数和临界速度的概念。

二十世纪中期，Inglis^[6]在Kolousk研究工作的基础上，将列车模型抽象成移动的周期性荷载，考虑列车模型和桥梁模型的质量，在此基础上将物理的受力模型用数学的方法转化成振动微分方程的形式，用试算的方法求解车桥的动力响应，求得的结果与试验的实测值接近。Krylov^[7]和Timoshenko^[8]将列车模型抽象成周期性的简谐荷载，研究了在简谐荷载作用下，桥梁的动力响应问题。20世纪60年代，Mise和Kunii^[9]等对前人的理论成果进行了归纳汇总，并提出了一种新的计算方法。Muchnikov在考虑桥梁模型和移动荷载质量的同时，利用数学中积分方程的方法来求解车桥振动问题中桥梁的动力响应问题。

从之前的研究可以看出，由于各种条件的限制，之前的研究对于车辆和桥梁模型的抽象过于简化，又缺少必要的计算工具，导致理论计算的结果往往与实际的结果有较大的偏差。尽管上述的研究存在一定的问题，但是像之前研究中所提出的一些基本概念，例如冲击系数和车桥共振等概念却一直沿用至今。20世纪60年代以后，计算机技术得到了快速发展，有限元理论也逐渐成熟，为工程问题与计算机技术的结合提供了基础。车桥耦合振动问题也越来越深入，人们不再将车和桥隔离开来，仅仅把列车作为激励分析桥梁的动力响应，车桥振动问题作为一个整体分析的观点被大多数专家学者所接受。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：