摘 要

阵列信号处理有两个主要的研究方向，空间谱估计便是其中之一。空间谱估计也被称为DOA估计，即波达方向估计，其主要原理是利用空间阵列接收到信号的参数，然后对其进行一系列处理，以获得目标信号空间谱的相关信息。但传统的DOA估计方法需要大量快拍数来获得较好的估计性能，为了突破奈奎斯特采样定理的限定，有学者提出了压缩感知理论，并将此理论与DOA估计相结合，从而有了基于压缩感知的DOA估计。这使得在少快拍的情况下就能实现良好性能的DOA估计，同时因其高分辨率、强鲁棒性的优点而得到学者的广泛关注。

而现存的一些基于压缩感知的DOA估计也存在一些问题，比如需要知道信源个数、噪声方差等先验参数，这在实际应用中可能难以实现。而本文研究的两种基于压缩感知的自由超参数DOA估计方法——SPICE方法和SBLRVM方法，则不需要知道这些先验参数，而能够在单快拍情况下拥有良好的DOA估计性能，并且对于有鲁棒性。本文针对这两种方法进行了仿真研究，证明了其有效性。并通过不同信噪比时的均方根误差和信源角度较近时的分辨率比较了两者的性能。

关键词：阵列信号处理；DOA估计；压缩感知；自由超参数

Abstract

There are two main research directions in array signal processing, one of which is spatial spectrum estimation. Spatial spectral estimation is also called DOA estimation, which is Direction-of-Arrival estimation. It obtains the spatial spectrum information of the target signal by processing a series of parameters of the received signal of the array. However, traditional DOA estimation methods need a large number of snapshots to achieve better estimation performance. In order to break through the limitation of Nyquist sampling theorem, scholars put forward compressed sensing theory, and introduced this theory into DOA estimation, so that a compressed sensing-based DOA estimation appeared. This makes DOA estimation with good performance in the case of fewer snapshots, and attracts wide attention because of its high resolution and strong robustness.

However, there are still some problems in the existing compressed sensing-based DOA estimation, such as the need to know the number of sources, noise variance and other prior parameters, which may be difficult to achieve in practical applications. However, the SPICE method and SBLRVM method, which are two hyperparameter-free DOA estimation methods based on compressed sensing, need not know these priori parameters, but have good DOA estimation performance in single snapshot, and are robust to coherent signal sources. In this paper, the two methods are simulated and proved to be effective. The performances of the two methods are compared by means of root mean square error (RMSE) at different SNR and resolution at near source angle.

Key Words: Array signal processing; DOA estimation; Compressed sensing; Hyperparameter-free

目 录

第1章 绪论 1

1.1 研究背景及意义 1

1.2 国内外研究现状 1

1.2.1 阵列信号DOA估计的研究发展及现状 1

1.2.2 基于压缩感知的DOA估计的研究发展及现状 2

1.3 本文主要研究工作及内容安排 3

第2章 阵列信号DOA估计的基本原理和方法 5

2.1 关于本文研究的假设 5

2.2 DOA估计的数学模型 5

2.2.1 通常情况下的模型 5

2.2.2 均匀线阵的模型 7

2.3 经典DOA估计方法 8

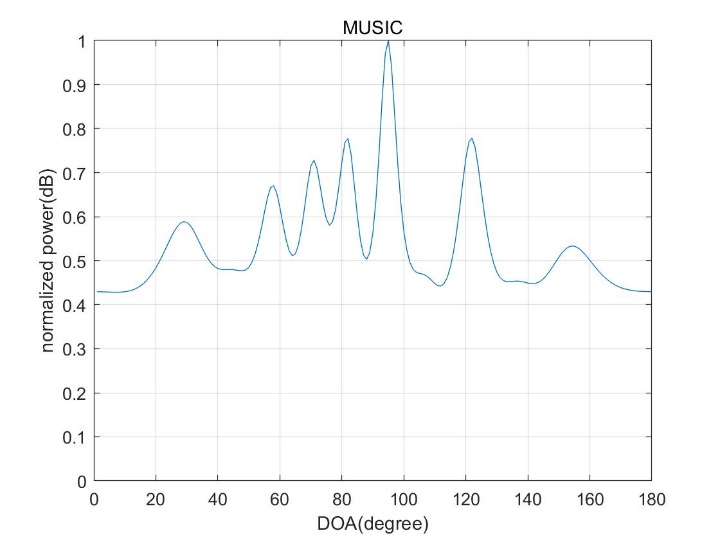
2.3.1 MUSIC算法 8

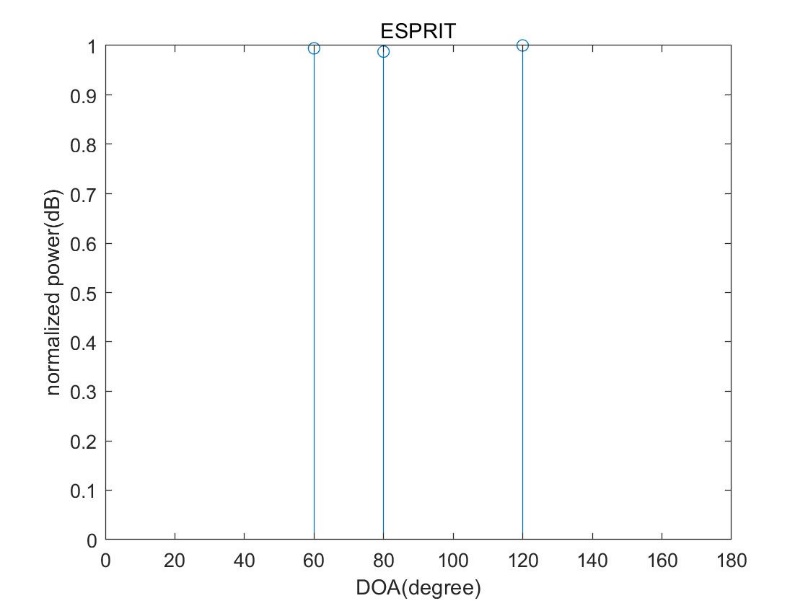
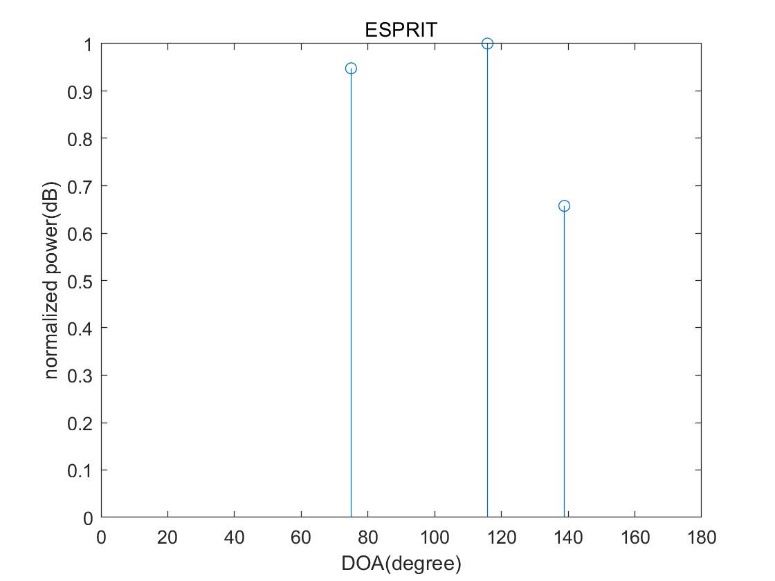
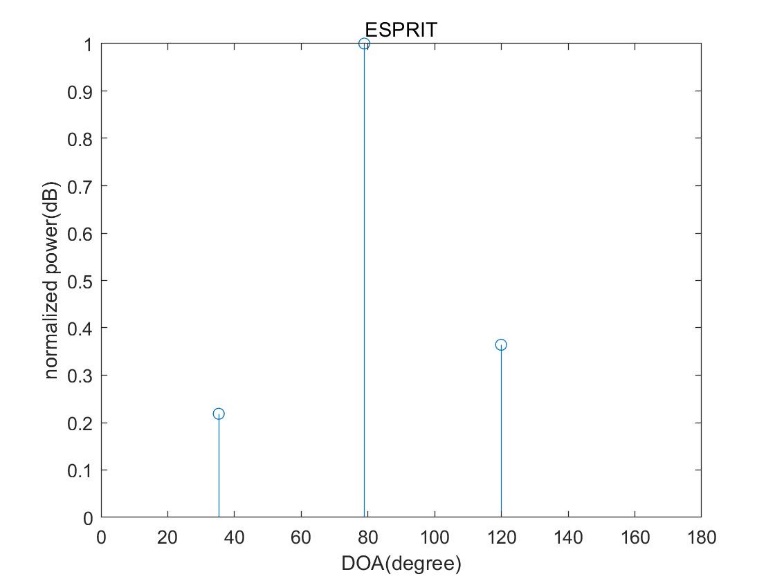
2.3.2 ESPRIT算法 11

2.4 本章小结 14

第3章 压缩感知理论 15

3.1 压缩感知基本理论 15

3.1.1 信号的稀疏表示 15

3.1.2 测量矩阵的设计 15

3.1.3 信号的重构 16

3.2 信号重构算法 16

3.2.1 基追踪算法 16

3.2.2 正交匹配追踪算法 17

3.3 基于压缩感知的DOA估计数据模型 17

3.4 本章小结 17

第4章 基于压缩感知的自由超参数DOA估计方法 19

4.1 数据模型 19

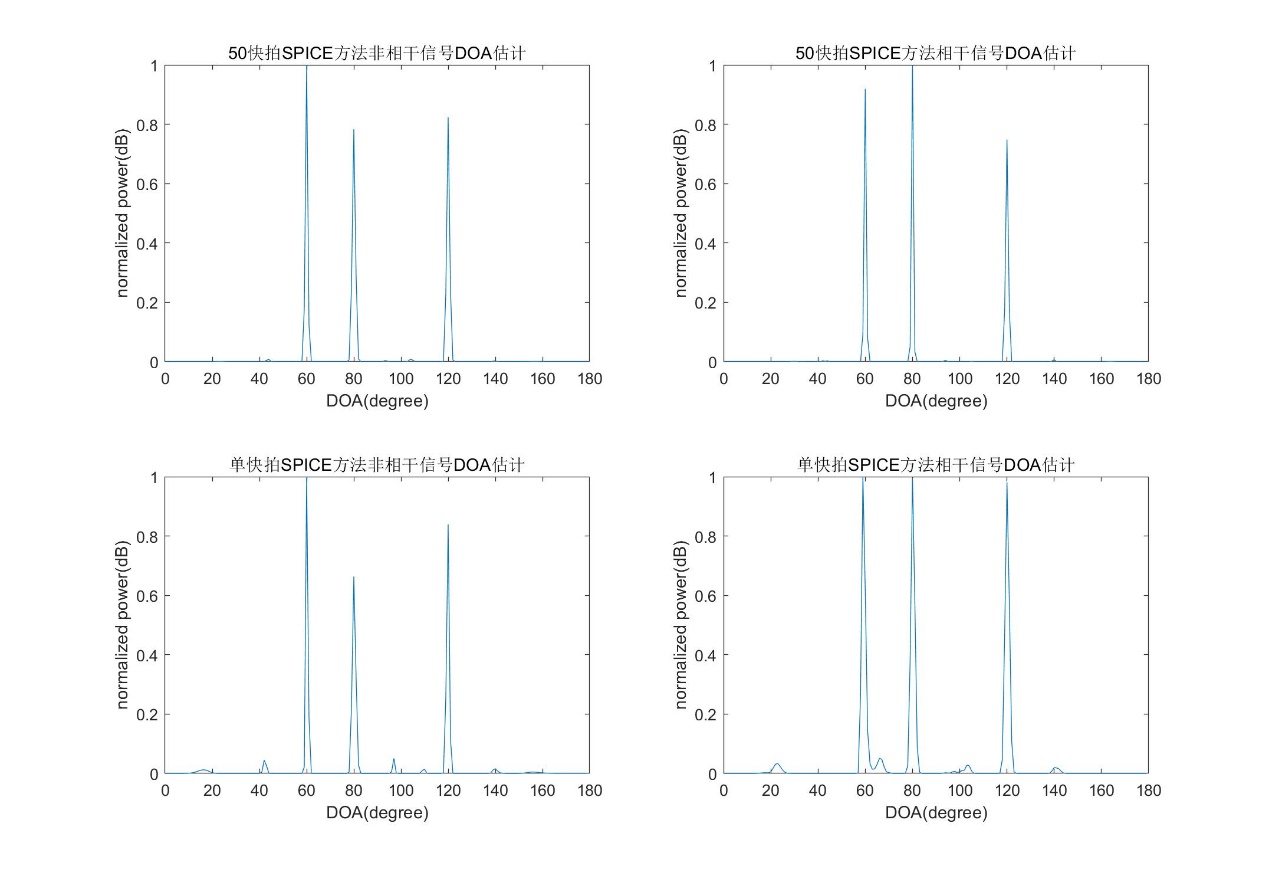
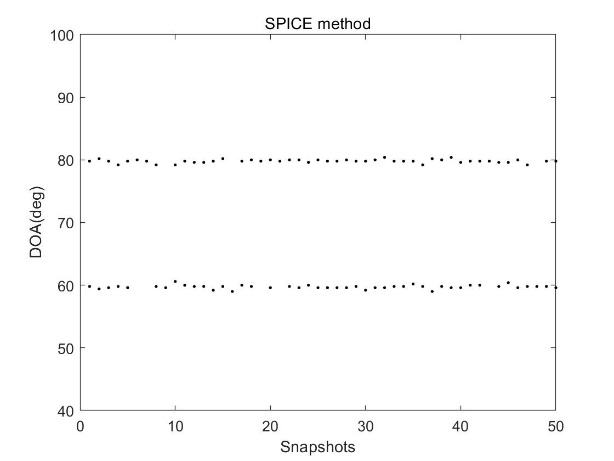
4.2 SPICE算法 20

4.2.1 基本原理及模型 20

4.2.2 仿真结果 22

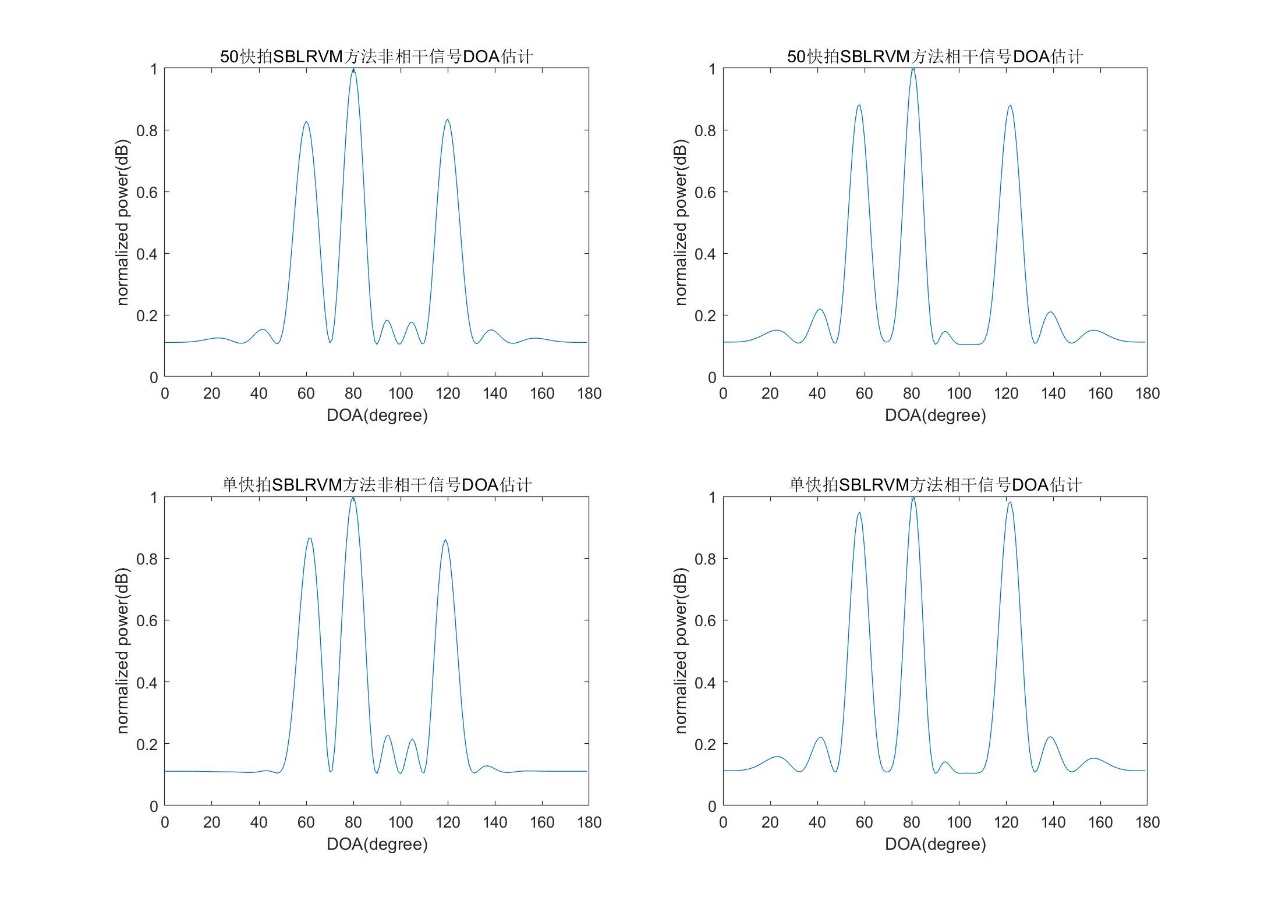
4.3 SBLRVM算法 22

4.3.1 基本原理 23

4.3.2 仿真结果 24

4.4 两种方法性能分析 25

4.4.1 单快拍估计直观对比 25

4.4.2 均方根误差对比 26

4.4.3 分辨率对比 27

4.5 GUI界面 28

4.6 本章小结 30

第5章 总结与展望 31

5.1 工作总结 31

5.2 未来展望 31

参考文献 33

致谢 36

第1章 绪论

1.1 研究背景及意义

随着信息化时代的发展速度越来越快，阵列信号处理在近几十年来的研究中取得了飞速发展，已广泛应用于诸多军事和民用领域，如水下声纳探测、医学成像、蜂窝移动通信、地震勘测等。阵列信号处理的基本思想是，空间中布置有一组按一定规律排布的传感器阵列，用其来接受空间信号，再对接收到的信号进行相关处理获得理想的结果。

阵列信号处理作为空域信号处理的基础，有两个主要研究方向，空间谱估计便是其中之一。其通过对阵列入射信号的参数进行一系列处理，以获得入射信号空间谱的相关信息。与时域中的频谱一样，空间谱也在阵列信号处理有着十分重要的地位，它代表着信号在空间不同方向上的能量分布情况。若能够根据估计获得信号的空间谱，便能够知道信号的波达方向（Direction Of Arrival, DOA）。

空间谱估计也叫作“DOA估计”，它的目标是确定感兴趣的信号的来波方向，即实现入射角度的估计。传统方法主要有常规波束形成（Conventional Beamformer, CBF）算法^[1]、最大似然估计（Maximum Likelihood , ML）算法^[2]、MUSIC(Multiple Signal Classification)算法^[3]、ESPRIT(Estimating Signal Parameters via Rotational Invariance Techniques)算法^[4]等。这些算法为了获得不错的估计性能，经常需要许多的快拍数据。然而，在处理过程中，某些情况下只能对目标得到有限的快拍，并且目标信号可能具有一定的相关性。在这种情况下，DOA估计传统方法的实现性能经常不尽如人意。为了解决这个问题，一种新兴的信号处理理论诞生了，它便是压缩感知(Compressed Sensing, CS)理论。

压缩感知理论通过将问题化为稀疏信号的恢复问题来进行DOA估计，即CS-DOA。它能够突破传统奈奎斯特采样定理的限制，实现在较少快拍数据的情况下就估计出目标信号的相关参数，或是重构出原始信号。由于其高分辨率、强鲁棒性，以及在有限快拍数下的优越性能等许多优点，CS-DOA估计方法得到广泛关注。

1.2 国内外研究现状

1.2.1 阵列信号DOA估计的研究发展及现状

从20世纪60年代开始，DOA估计开始进入研究，经过几十年的发展，已经有了一些优秀成果。

将传统时域傅里叶谱的估计方法简单扩展到空域，就有了首先出现的基于阵列的DOA估计算法即常规波束形成（CBF）算法，也被称为Bartlett波束形成法^[1]。但它会受到“瑞利（Rayleigh）限”的限制，当信号在空间中处在一个波束宽度范围内时，该算法无法对其实现估计。

为了突破“瑞利限”，学者们展开研究，因此从20世纪70年代开始，便有新的突破，即出现了高分辨谱估计方法。主要有：Capon的最小方差法（Minimum Variance Method, MVM）^[5]、Burg的最大熵法（Meximum Entropy Method, MEM）^[6]等。

20世纪70年代末期，子空间类算法的大门被打开，这使得DOA估计算法研究有了突破性进展。根据处理方式的不同，子空间分解类算法可分为两类：一类是以MUSIC为代表的噪声子空间类算法^[3]；另一类是以ESPRIT为代表的信号子空间类算法^[4]。这类算法的基本思想是将接收到的数据划分成信号子空间和噪声子空间，然后利用两个子空间之间的正交性形成“针状”谱峰，这在很大程度上提高了算法的分辨率。

20世纪80年代后期，一种子空间拟合类的算法出现了。其中代表有：最大似然（Maximum Likelihood, ML）算法^[2]、加权子空间拟合（Weighted Subspace Fitting, WSF）算法^[6]等。与子空间类算法相比，子空间拟合类算法有着十分显著的优点，例如在少快拍、低信噪比，或者在相干信源的情况下，能够有更有效的估计性能，可以更好地估计出信号的入射角度。但是，运算量大也是其不可忽视的缺点。

在现实中，除了窄带信号，也存在着宽带信源，这使得上述针对窄带信号的DOA估计方法在宽带信号情况下不能很好的获取有用信息。因此，DOA估计算法也被推广到了宽带信号中，显著成果是将子空间类算法推广到了宽带，主要有三类：非相干信号子空间算法（Incoherent Signal-Subspace Method, ISSM）^[7]、相干信号子空间算法（Coherent Signal-Subspace Method, CSSM）^[8]和投影子空间正交性测试方法（Test of Orthogonality of Projected Subspaces, TOPS）^[9]。

1.2.2 基于压缩感知的DOA估计的研究发展及现状

2006年，在前人关于稀疏表示的想法和研究成果的基础上，Donoho等人首先提出了压缩感知（CS）的概念^[10]。然后，Candès等人运用严谨的数学推算，对压缩感知理论的基本原理加以证明，并得出了稀疏重构的限制条件，其中便包括了著名的有限等距条件(Restricted Isometry Property, RIP)^[11]。至此，压缩感知理论被正式提了出来。

但其实，将压缩感知理论引入运用到DOA估计的研究早些时候便开始了。自从2004年匹配追踪算法的雏形在Karabulut G Z等人的研究中诞生之后，贪婪算法便开始大量运用到了阵列信号DOA估计中，其中就包括高效精准的子空间追踪（Subspace Pursuit, SP）^[12]、匹配追踪（Matching Pursuit, MP）^[13]、正交匹配追踪（Orthogonal Matching Pursuit, OMP）^[14]、正则化正交匹配追踪（Regularized Orthogonal Matching Pursuit, ROMP）^[15]等改进算法。

2005年，Malioutov等人提出一种对信号的有效的稀疏表示方式，称为-SVD^[16]。该算法对优化问题加以求解，获得信号源的方位。在少量快拍的情况下，这种算法也可以精确地估计得到信源DOA，并且对于相干信号也具有直接处理能力。但由于需要较大的运算量，这限制了其在实际中的应用。

2011年，Yin和Chen根据协方差矩阵匹配技术（Covariance Matching Estimation Technique, COMET）^[17]提出了一种称为-SRACV的方法，这是一种基于阵列协方差矩阵稀疏表示的DOA估计方法^[18]。它可以不用知道信源数量这一先验条件，并且对于相干信号也能够处理。然后，Stoica等人也基于COMET技术提出了一种基于协方差稀疏迭代的DOA估计方法（Sparse Iterative Covariance-Based Estimation Method, SPICE）^[19]。这种方法不需要知道信源和噪声功率以及信源数这些先验条件，通过最小化协方差拟合标准来完成估计，能够达到很高的估计精度。这是本文要讨论的DOA估计算法之一。

2001年，由 Tipping M E最早提出了基于稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)理论的DOA估计思想^[20]。这种思想的并在近几年发展成熟。2007年，David P. Wipf 和 Bhaskar D. Rao提出了基于稀疏贝叶斯学习的相关向量机方法（Sparse Bayesian Learning-based Relevance Vector Machine, SBLRVM）^[21]。这是一种全自动相关性确定算法,它基于贝叶斯证据最大化框​​架。这也是本文要讨论的算法之一。

1.3 本文主要研究工作及内容安排

本文介绍了阵列信号DOA估计模型和压缩感知理论，两者相结合得到了基于压缩感知的DOA估计模型，然后在此模型的基础上，详细介绍和研究了两种基于压缩感知的自由超参数DOA估计方法——SPICE方法和SBLRVM方法，在Matlab环境下对两者进行仿真研究，得到信号的波达方向，证明了算法的有效性，并比较两者的性能。

本文内容安排如下：

第1章是绪论，介绍了几十年来传统阵列信号DOA估计以及基于压缩感知的DOA估计（CS-DOA）的研究发展及现状，阐述了本文的研究背景和意义，。

第2章首先提出了本文研究所做的几个假设，然后在此假设基础上介绍了阵列信号DOA估计的一般数学模型，然后介绍了两种经典的DOA估计方法——MUSIC算法和ESPRIT算法，并对其进行仿真研究。

第3章主要对压缩感知理论进行了详细的阐述，介绍了它的基本思想、三个核心部分及信号重构的算法。然后提出了将压缩感知理论应用到DOA估计的一般数学模型，为下文研究打下基础。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：