摘 要

随着现代化进程的发展，大量报废机械、汽车、电器等产品亟待回收处理。为解决在产品回收的过程中存在的拆卸任务分配不均的问题，本文将介绍利用基于分解的多目标进化算法对拆卸线平衡问题（DLBP）进行研究，找到指定条件下的Pareto最优解或解集。

本文首先介绍了研究拆卸线平衡问题的目的与意义，在此基础上分析了相关的国内外研究成果，分析并比较目前成果中的不足；基于多目标优化算法的特点，在考虑零件的拆卸优先级顺序和工作站的实际工作时间不能超过工作节拍的前提下，为拆卸线平衡问题建立了三个待优化目标的数学模型，分别是工作站数目最小化、工作站之间的工作负荷平衡化以及危害性最小化；接下来本文就如何利用MOEA/D算法求解拆卸线平衡问题展开设计，分为总体设计和局部算法设计；最后，本文基于Matlab工具仿真实现了利用MOEA/D算法求解DLBP问题。

经过对已有论文中的数据测试，MOEA/D算法能在较短时间内求解出问题的最佳分配方案。本设计能实现最初设定的目标，验证了MOEA/D算法的可行性和准确性。

关键词：MOEA/D； DLBP； Matlab； Pareto

Abstract

With the development of modernization, a large number of end-of-life machinery, automobiles, electrical appliances and other products are facing the problem of waiting for recycling. In order to solve the problem of uneven distribution of disassembly tasks in the process of product recycling, this paper will introduce a decomposition-based multi-objective evolutionary algorithm to study the disassembly line balance problem (DLBP) and find Pareto optimal solution or disassembly set under specified conditions. It includes considering the working rhythm of the workstation and the priority of parts disassembly.

Firstly, this paper introduces the research background, purpose and significance of disassembly line balancing problem, and analyses the current research results and advantages and disadvantages at home and abroad. Secondly, this paper mainly introduces the basic theory and implementation method of decomposition-based multi-objective evolutionary algorithm, introduces the problem model of disassembly line balancing problem and establishes corresponding objective functions, including minimizing workstations and balancing. Workload between workstations, taking into account the priority order of parts and the time rhythm of workstations; Next, this paper introduces in detail the solution of the disassembly line balance problem by using MOEA/D algorithm, and introduces these designs by using UML use case diagram and flow chart; Finally, this paper introduces the simulation of the disassembly line balance problem by using MOEA/D algorithm based on MATLAB development platform. The research is mainly divided into problem modeling and Pareto optimal solution using MOEA/D algorithm.

After testing, the MOEA/D algorithm can get the best solution of the disassembly line balance problem. The design can basically meet the design requirements, and verify the feasibility and accuracy of MOEA/D algorithm.

Key words: MOEA/D； DLBP； Matlab； Pareto

目 录

摘要 I

Abstract II

第1章 绪论 5

1.1 研究目的及意义 5

1.2 拆卸线平衡问题的研究现状 2

1.3 论文内容安排 3

第2章 拆卸线平衡问题定义与建模 4

2.1拆卸线平衡问题定义 4

2.1.1 拆卸线及拆卸线的基本特点 4

2.1.2 拆卸线的主要分类 5

2.1.3 拆卸线平衡问题 5

2.2拆卸线平衡问题建模 6

2.2.1 模型概述 6

2.2.2 求解思路 8

2.3本章小结 8

第3章 基于MOEA/D的算法设计 9

3.1 多目标进化算法简介 9

3.1.1 多目标优化问题 9

3.1.2 Pareto最优解集 10

3.2 MOEA/D算法 11

3.2.1 MOEA/D算法介绍 11

3.2.2 MOEA/D算法基本原理与实现 12

3.3 总体设计 13

3.4 算法设计 14

3.4.1 问题示例 14

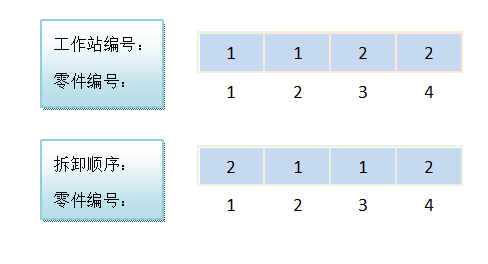
3.4.2 编码设计 14

3.4.3 解码设计 15

3.4.4 轮盘赌选择 16

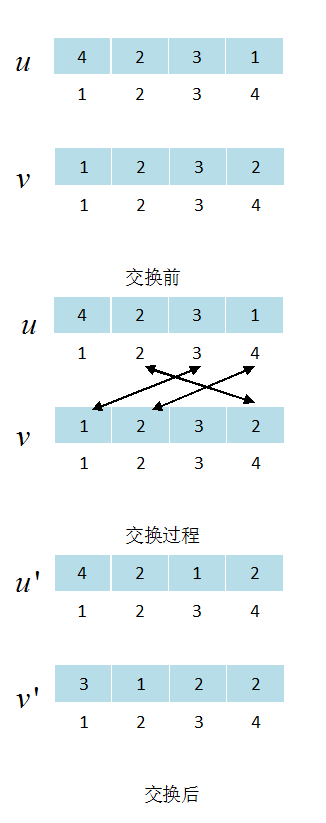
3.4.5 交叉设计 17

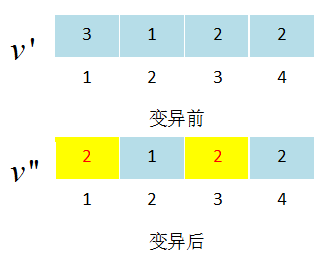
3.4.6 变异设计 17

3.5 本章小结 19

第4章 算法仿真与分析 20

4.1 算例与仿真环境设置 20

4.1.1 仿真环境设置 20

4.1.2 小规模算例 21

4.1.3 大规模算例 21

4.1.4 性能分析指标介绍 23

4.2 仿真结果与分析 23

4.2.1 小规模算例仿真结果 23

4.2.2 大规模算例仿真结果 26

4.3 本章小结 28

第5章 总结与展望 30

5.1 论文总结 30

5.2 研究工作展望 31

参考文献 32

致谢 34

附录A 35

第1章 绪论

1.1 研究目的及意义

随着国家提出“中国制造2025”战略，实现机器的自动化建设，意味着越来越多的机器将面临重建和报废，由此带来的大量机械产品亟待回收处理。另外，经过许多年的能源开采，目前地球资源逐渐面临短缺的问题，所以传统耗能高，效率低的机器也要退出历史舞台，所有这些面临报废的机械产品，并不都是直接弃之不顾，其拥有的有些零部件可以经过拆卸回收利用。而在这个过程中，最重要的就是拆卸过程，实现拆卸过程的平衡化和流水化，将最大限度的提高产品的回收利用率，这样不仅能尽快解决报废产品的回收问题，同时又能加快机械职能化转型。所以，研究拆卸线平衡问题，并提出一种切实可行的最优分配方案对于国家的产业智能化转型具有十分重要的意义。

在产品的拆卸过程中，由于经常需要考虑多方面的因素，比如工作站数目最小化、危害性指标以及工作站之间的负载平衡等问题，使得实际分配的方案往往存在拆卸零件分配不均衡的问题，由此带来的回收利用率低下以及一系列问题，一直是限制实现拆卸过程流水化的重要原因，市场亟需一种准确最优的拆卸任务分配方案。

拆卸线平衡问题是一类复杂的NP-hard问题，因为常常需要考虑多方面的因素，加上对于机械产品来说零件数目通常非常大，其对应的分配方案非常多，这无疑增加了找到最优分配方案的难度。本文以此为研究背景，研究如何基于分解的多目标进化算法MOEA/D来解决多个目标的拆卸线平衡问题。

1.2 拆卸线平衡问题的研究现状

“拆卸线平衡问题的最早是由Gungor和Gupta提出，并给出了相关的数学描述。Gungor和Gupta最初关注的是待拆卸零件对拆卸线的损失问题，基于该问题，提出拆卸线平衡问题。接着，他们俩又加入了产品种类、生产布局方式、任务分配受限性、零部件状况、拆卸操作、需求以及危害性等方面论述了影响拆卸线平衡的各个因素。在此基础上，设计了一种基于多维优先级值累加筛选策略的启发式对问题进行求解。具体思路是：首先，筛选出缝合优先关系约束和工作站节拍约束的任务。然后，从剩余空闲时间、需求数量、最大紧后任务数、零部件危害性、方向改变次数五个方面分别计算每个任务的优先级值，并进行求和。最后，找出优先级值之和最小的任务进行分配”。

“对于拆卸线平衡问题的研究从Gungor和Gupta提出拆卸线平衡问题开始，陆续出现了许多优秀的算法进行求解。主要分为两种：启发式算法和数学规划算法。Avikal提出的传统的启发式算法对于小规模的拆卸线平衡问题可以快速找到最优化的分配方案，但对于大规模的问题显得相对无力；Bentaha提出的数学规划方法同样对于小规模拆卸线平衡问题有很好的优化效果，但对于大规模的拆卸线平衡问题，往往无法给出相对优良的解法。原因在于拆卸线平衡问题的复杂度是随着问题规模呈集合方式增加的，所以，传统的这些算法只能限于求解相对规模较小的拆卸线平衡问题。基于拆卸线平衡问题的特殊性以及启发式算法的优点，人们陆续提出了许多亚启发式算法，其在解决大规模拆卸线平衡问题时表现出了非常好的效果，比如遗传算法、蚁群算法、粒子群算法、人工蜂群算法以及多目标进化算法等在解决大规模拆卸线平衡问题是也能求出最优解。虽然这些算法在求解多个优化目标的拆卸线平衡问题有很好的效果，但是究其本质，都是对多个优化目标施加不同的权重，相当于将多目标问题转化为等效单目标进行求解，这并不符合多目标拆卸线平衡问题的定义” 。

“近些年，在简单拆卸线平衡问题的研究基础上，问题的研究方向慢慢拓展到多品种、复杂布局的拆卸线平衡问题上。Hezer首次提出了并行布置拆卸线平衡问题，并用一种基于网络的最短路模型同时平衡不知多条拆卸线。该方法采用一种枚举策略，逐一筛选所有可行的分配方案，最终得到问题的最优解，但不适合用于对大规模问题的求解”。

基于分解的多目标进化算法（MOEA/D）最早是由Qingfu Zhang等人提出的。该算法将传统的多目标优化问题转化为多个子目标的优化问题。MOEA/D算法是一种优秀的多目标进化算法，其是在利用分解策略，将复杂的多目标或单目标问题转化为多个子问题分别进行优化。这种分解方式十分适合拆卸线平衡这种复杂的多目标问题。并且多目标进化算法是在综合考虑多方面因素得出的Pareto解平面，具有十分良好的实用性。

1.3 论文内容安排

本论文一共分为五章，内容安排如下：

第一章：绪论。主要介绍本文研究拆卸线平衡问题的原因以及拆卸线平衡问题的相关问题，最后阐明了本次论文的内容安排。

第二章：拆卸线平衡问题定义与建模。介绍拆卸线平衡问题的基本概念，并对拆卸线平衡问题进行数学建模，从中提取出可优化的三个目标函数以及求解过程应考虑的一些限制条件。

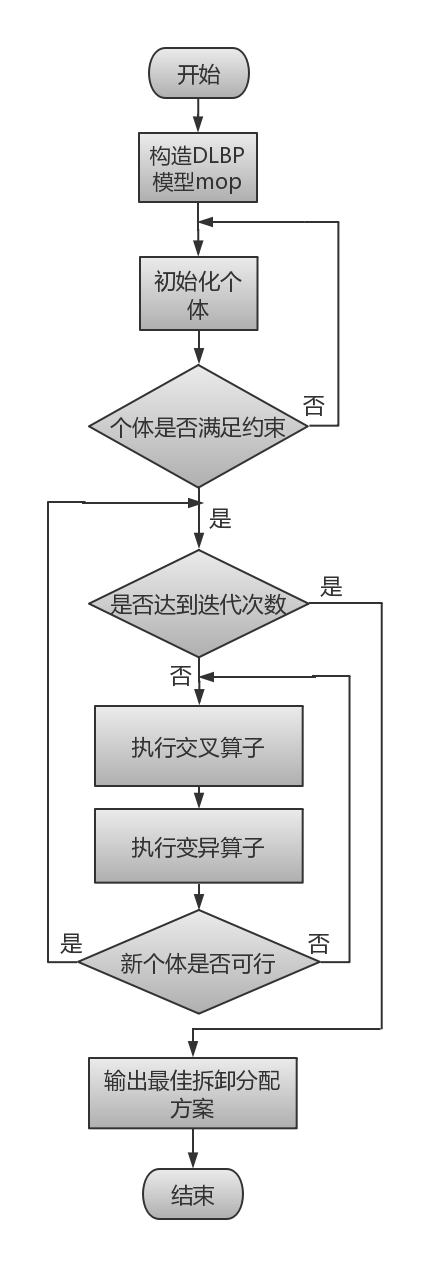
第三章：基于MOEA/D的算法设计。本文详细介绍了多目标进化算法与基于分解的多目标进化算法之间的关系以及基于分解的多目标进化算法的实现步骤，包括多目标进化算法的三种分解策略。并基于MOEA/D算法的特点，给出了利用MOEA/D算法求解拆卸线平衡问题的求解思路。将MOEA/D算法与拆卸线问题模型相结合，设计出能解决拆卸线平衡问题的MOEA/D算法，设计内容包括：整体设计、编码解码、交叉以及变异算子等。并给出整体设计的流程图。

第四章：算法仿真与分析。基于Matlab仿真工具，实现MOEA/D算法对拆卸线示例的任务分配仿真，分别对小规模拆卸线平衡问题和大规模拆卸线平衡问题进行了仿真分析，并同蚁群算法进行对比。

第五章：结论与展望。主要是谈谈在本次设计中的收获与感悟，并对基于本设计更加深层次研究作展望。

第2章 拆卸线平衡问题定义与建模

2.1拆卸线平衡问题定义

2.1.1 拆卸线及拆卸线的基本特点

产品的拆卸是指对于废弃的机械或者人工产品中的可回收部分进行拆卸重新利用的过程。零件拆卸通常是用人工进行拆卸，包括单个工作站的模式以及拆卸流水线的模式。其中单个工作站由于规模小，适用于小型机械产品的拆卸，对于大规模的机械产品，须采用拆卸线的模式进行拆卸，以多个工作站协同作业，共同拆卸一款大型器械开始重新得到重视并应用于工业的流水线拆卸过程。图2.1 为拆卸线示意图

图2.1 拆卸线示意图

拆卸线主要有以下几个特点：

1）专业化程度高。相对于单一的工作站来说，拆卸线是属于流水线作业，每个工作人员只需要完成对某一特定的零件进行拆卸，这样不仅可以较少不同零件拆卸过程中所需要的转换时间，同时可以增强工作人员对于自己所负责零件的熟练度。

2）生产具有节奏性。拆卸线进行拆卸的时候是每隔一段时间才投放一次产品，并不是一次性投放，这样整体保持一定的工作节奏，同时工作人员也保持相应的工作节奏，节省了工作人员每次拆卸都需要重新适应的时间。

3）工艺生产过程的封闭性。因为是采用拆卸线的拆卸方式，所以每个工作人员都相对而言精通单一或几个零件的拆卸，就像传送带分别将不同的零件传到不同的工作人员手中。工艺过程相似程度较低的产品，无法安排在同一个工作站进行拆卸，需要重新分配新的工作站。

2.1.2 拆卸线的主要分类

拆卸线的分类方式主要是根据拆卸产品的属性来分，具体分类如表2.1所示：

表2.1 拆卸线的具体分类

2.1.3 拆卸线平衡问题

拆卸线平衡问题主要解决的问题是在现阶段的拆卸过程中，存在着拆卸任务分配不合理的导致存在很大的资源浪费以及拆卸效率低下。拆卸线平衡问题就是在满足所有的拆卸线任务不违背约束条件的情况下，将拆卸任务均衡的分配给各个工作站，实现工作站的效率最高化，从而达到预期目标。通常情况下，要求实现的预期目标有很多个，包括开启工作站数目最小化，各工作站的工作负荷要均衡以及优先处理危害性高的零部件。

拆卸线问题的一些基本概念：

1）待拆卸零件：待拆卸零件是拆卸线平衡问题不可分割的最小量，待拆卸零件的最终的拆卸顺序就是拆卸线平衡问题的解。

2）零件拆卸时间：零件拆卸时间指的是一个待拆卸零件被拆卸所需要花费的时间，是待拆卸零件的一种属性，不会因为分配的工作站而产生变化。

3）零件拆卸优先级：零件拆卸优先级指的是在产品拆卸过程中，零件i需要比零件j先拆除，则称零件i的拆卸优先级高于零件j。

4）待拆卸零件危害性：一般情况下，废弃的产品的零部件组成都很复杂，可能包括一些对环境或者人体有伤害的零件，需要先行拆卸，所以引进危害性指标来衡量待拆卸零件的危害性。

5）工作站：工作站是待拆卸零件完成拆卸的地方，待拆卸零件被分配到工作站上完成拆卸操作。

6）工作节拍：工作节拍是指一个工作站能最大承受的工作时间，由具体情况而定，每台工作站的情况可能会有不同。本文中假定的所有工作站都具有相同工作节拍。

7）工作站拆卸作业时间：工作站拆卸作业时间指的是某一台工作站所负责待拆卸零件的拆卸时间之和（必须小于工作节拍）。

8）工作站空闲时间：指的是工作站工作节拍与工作站实际分配的待拆卸零件所耗费的拆卸时间之差的平方，其值越小，表示工作站的工作效率越高。

2.2拆卸线平衡问题建模

2.2.1 模型概述

从上一节的介绍中，可以看出拆卸线平衡问题的复杂性。基于拆卸线的一些基本概念以及本研究要实现的目标：工作站数目最小化、工作站之间的工作负荷平衡化以及危害性最小化，本文建立如下数学模型：

假设需要解决的拆卸线平衡问题的规模为n，即有n个待拆卸零件，需要开启的工作站数目为m，每个工作站的工作节拍为C，第i工作站上分配的待拆卸零件实际拆卸时间和为t_i。同时用T_ij表示任务与工作站之间的关系，若T_ij = 1,表示待拆卸零件j被分配到工作站i上。本文从三个方面构建拆卸线平衡问题的模型：工作站数目最小化、工作站之间的工作负荷平衡化以及危害性最小化。带拆卸零件之间的优先关系用P表示，若P_(p,q)=1，则表示零件p需要在零件q之前拆卸。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：