基于聚类算法的手写数字识别方法研究与实现毕业论文
2020-02-17 22:00:46
摘 要
手写数字识别是图像处理和模式识别领域中的研究课题之一。手写体数字识别在财务报表、银行票据、邮政编码、各种凭证以及调查表格的识别等等方面有着十分重要的作用。由于手写数字识别面临着因书写风格不同导致的识别困难使得手写数字识别成为模式识别邻域内具有挑战性的课题。
本文描述了手写数字识别的研究背景和发展状况,给出了三种可行的聚类算法。基于MNIST数据集,通过Matlab平台,辅以Pycharm平台,通过K-Means算法、自组织映射网络(SOM)算法和高斯混合模型(GMM)的EM聚类算法进行实现,并对聚类算法的准确性进行评估。
实验结果显示,K-Means算法平均识别准确率为93.45%,高斯混合模型的EM算法平均准确率为83.49%,SOM算法的平均识别率则为87.86%。此结果表明,基本实现了三种算法对手写数字数据集的识别,但是聚类算法整体识别率不高,有待进一步的改进与优化
关键词:手写数字识别;聚类算法;K-Means算法;SOM算法;EM聚类算法
Abstract
Handwritten digit recognition is one of the research topics in the field of image processing and pattern recognition.Handwritten digit recognition plays an important role in the financial statements, bank notes, postal codes, various vouchers, and the identification of survey forms.Because the handwritten numbers are different in writing author style, the digital images are very random, such as: font size, font tilt and stroke thickness, etc. , making handwritten digit recognition a challenging topic in the pattern recognition neighborhood.
This paper describes the research background and development of handwritten digit recognition, and presents three feasible clustering algorithms.Based on the MNIST dataset, clustering is achieved by Matlab platform, supplemented by Pycharm platform, K-Means algorithm, self-organizing mapping network (SOM) algorithm and Gaussian mixture model (GMM) EM clustering algorithm,and evaluate the accuracy of the clustering algorithm.
The experimental results show that the average recognition accuracy of K-Means algorithm is 93.45%, the average accuracy of EM algorithm of Gaussian mixture model is 83.49%, and the average recognition rate of SOM algorithm is 87.86%. The results show that the recognition of handwritten digital datasets by three algorithms is basically realized, but the overall recognition rate of clustering algorithms is not high, and further improvement and optimization are needed.
Keywords:Handwritten digit recognition;Clustering Algorithm;K-Means Algorithm;SOM Algorithm;EM Algorithm
目 录
第1章 绪论 1
1.1课题研究背景及意义 1
1.2 手写数字识别的难点 1
1.3国内外技术发展与研究现状 2
1.4本文的研究内容及组织结构 3
第2章 算法理论基础 4
2.1 K-Means算法 4
2.1.1基本原理 4
2.1.2算法流程 4
2.1.3算法应用 7
2.2自组织映射神经网络(SOM)算法 7
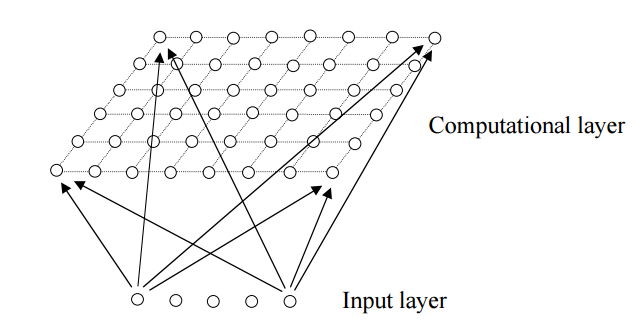
2.2.1 SOM网络结构及应用 8
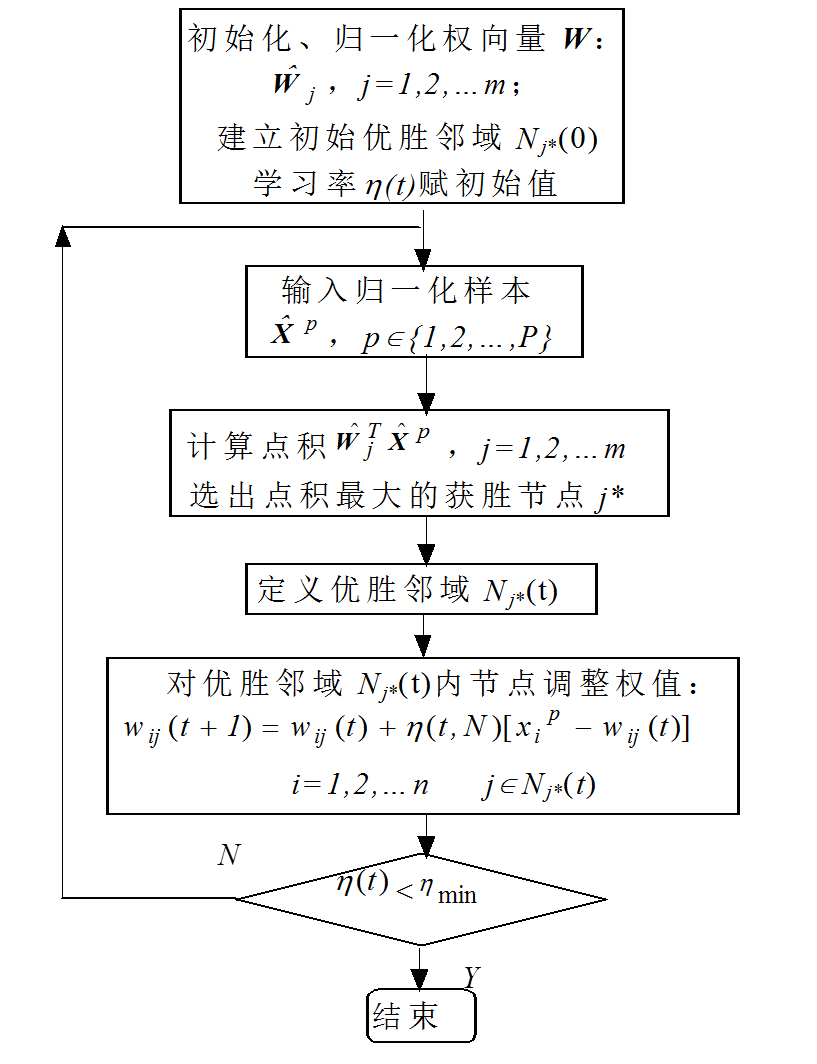
2.2.2 SOM的学习算法 8
2.2.3 SOM设计细节 9
2.3 高斯混合模型(GMM)及其EM算法 10
2.3.1高斯混合模型(GMM) 10
2.3.2 EM算法 11
第3章 手写数字识别算法实现 12
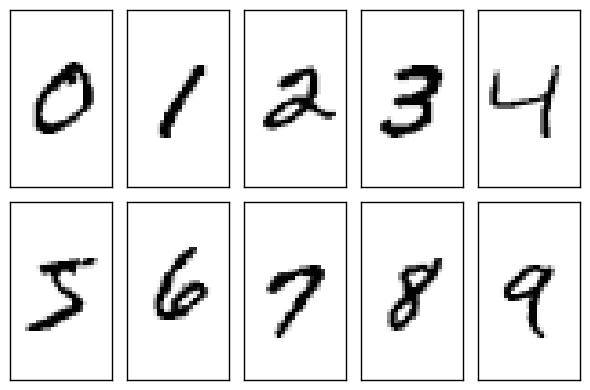
3.1 MNIST数据集 12
3.2 K-Means算法识别 13
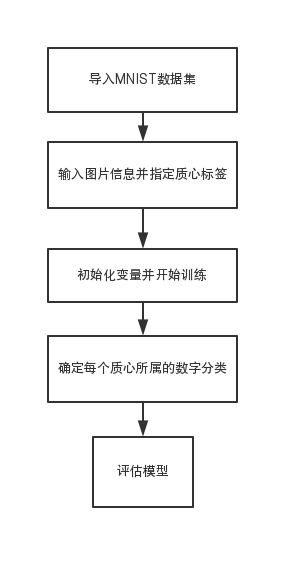
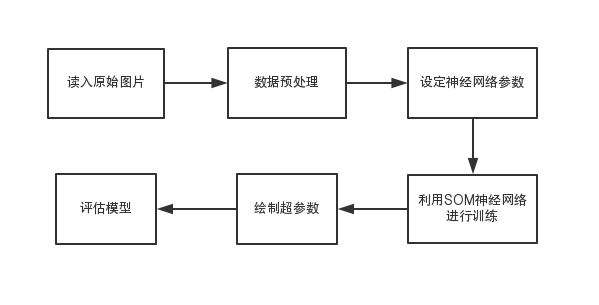
3.3 SOM算法识别的实现 15
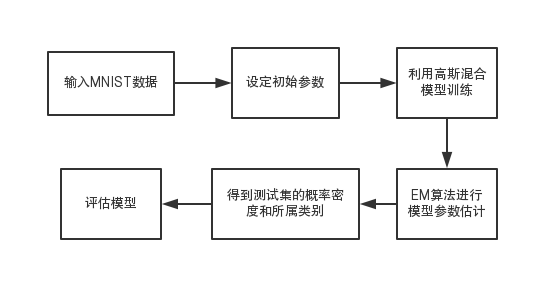
3.4 EM算法及高斯混合模型的建立 16
3.5 三种算法异同点 17
第4章 平台运行测试与结果 18
4.1 K-Means实验结果与分析 18
4.2 SOM算法实验结果与分析 19
4.3 EM算法实验结果与分析 20
4.4小结 22
第5章 总结与展望 23
5.1工作总结 23
5.2对未来的展望 23
致谢 24
参考文献 25
第1章绪论
1.1课题研究背景及意义
图像是信息表达、存储和传输的重要手段之一。随着计算机技术和数字图像处理技术的发展,对数字图像分类和识别技术的需求越发迫切。图像识别应用十分广泛,例如手写识别、人脸识别、车牌识别等等,它是利用AI技术使计算机能够识别图像中蕴含的信息。图像分类和别技术作为图像信息处理的核心问题之一,是一种比较高级的视觉处理任务,因此在整个的图像处理领域都具有非凡的意义,并且具有十分广阔的应用前景。
手写数字识别作为图像分类中的一个实用问题,它所研究的核心问题是:如何利用计算机自动识别出10个阿拉伯数字,由于数字的清晰程度或者个人的书写习惯抑或其他,往往手写体数字的性状、大小、深浅会不一样。
手写数字识别具有十分广阔的前景,在财会、教育和金融等众多的领域具有广泛的应用背景和使用价值。因而,实现手写数字的识别能够为人们的工作和生活带来很大的方便。对该领域的研究具有重要的理论价值:
一方面,手写数字识别的研究自上个世纪五十年代开始,许多研究者在这个领域展开了广泛的研究和探索,并且得到了许多可喜的成就。但是目前为止,机器的识别率和正确率还远远不能达到实际应用的需要。
另一方面,由于手写数字识别所需识别的类别数相对较少,识别率会优先于其他字符识别,有利于做进一步的深入分析及验证一些新的理论。此外,许多新的机器学习、模式识别的理论和算法都以手写数字识别作为具体的实验平台,已验证理论的有效性,评价各种方法优缺点。
数字识别的算法有很多,当前运用较好的主流算法以统计、回归、聚类和分类算法为主,比如Softmax回归、Bagging算法、K-Means算法、支持向量机算法、神经网络算法等。本文主要采用的是聚类算法来实现手写数字识别,包括K-Means算法、SOM算法和EM算法。通过探究各个算法的工作原理,构建相对应的模型,实现对MNIST数据集的识别。
1.2 手写数字识别的难点
在现实生活中,当涉及到数字识别,我们往往都要求识别的整个系统有很高的识别精度,特别是在金融领域有关金额的数字识别如在发票中、支票中填写的金额部分时。因此这对手写数字识别系统的可靠性和识别率提出了不小的挑战,就目前识别技术的发展来看,其中的困难点主要有以下几个方面:
- 阿拉伯数字0-9相较我们常用的汉字和字母而言,它的笔划过于的简单,这也就意味着,它所蕴含的信息就很少,每个不同的数字之间没有特别大的差别,因此在做识别的时候,很难做到准确的区分这些数字;
- 由于人们的知识水平,书写习惯不同等诸多的因素,每个人手写出来的数字会存在着很大的不同,甚至同一种数字的写法也会千差万别,同时也要考虑到每个人在不同时间地点写出来的数字也可能具有差异性,因此识别的过程是个十分具有挑战性的问题;
- 脱机手写数字识别与联机相比又增加了不小的难度,联机识别的过程中可以根据输入者书写笔划的先后顺序信息来做分析识别,反观脱机识别,得到的仅仅是一张张简单的图片,能够用作处理的信息太少,故如何进行脱机手写数字的识别也值得探究。
1.3国内外技术发展与研究现状
最早期的文字识别技术可以追溯到上个世纪50年代初期,最先起源于美国。随着1946年第一台计算机的出现而诞生,发展到现在已然有一百多年的历史。无论是发展的哪个阶段,字符识别在工业,制造业等领域都极为重要,因此字符识别技术也一直深受大家关注。1929年由德国科学家Tausheck率先提出了光学字符识别(OCR)的概念并且获得了这项技术的专利权。在技术发展前期,由于技术人员知识理论的不足,当时的字符识别只能对特定规范下的手写体数字采用模板匹配的方法进行识别。
经过一个多世纪的发展,光学字符识别已成为了模式识别领域最为活跃的研究课题之一。在字符识别的快速发展时期,许许多多新型的识别算法被研究者们提出,而且这些算法还能够有效的提高识别的准确率,其中最为常见的是人工神经网络(Artificial Neural Network ,ANN)和支持向量机(Support Vector Machine ,SVM),而且这些识别算法至今仍然是研究的重点。
随着当今社会信息化进程的迅猛发展,越来越多的领域对手写数字识别有了新的需求,而这些识别系统的性能关键点以及目前发展的瓶颈在于识别的核心算法上,最终是为了能够探究出一种具有零误识率和低拒识率的算法。日本于1967年最先使用手写体数字识别,并且运用到邮政方面的阅读分拣机,取得了很大的成功,并在此基础之上,逐年对识别系统进行改进,到70年代以后已经广泛应用在邮政上。1974年年底,我国完成了国内第一个识别字体限制较少的手写数字识别的实验系统。在此基础之上,中国科学院自动化研究所于1977年8月为我国第一条自动邮政信函分拣流水线提供了手写体数字识别的样机。我国在80年代左右,字符自动识别技术得到了迅猛的发展,由清华大学陈鸣华和阎平凡教授提出的基于数学形态的识别方法,识别的结果是错识率1.49%,拒识率4.9%。经过国内外的研究学者对识别算法不断优化,识别的准确率也变得越来越高。2018年,由新泽西科研所提出的一种基于脉冲神经网络的识别算法,达到了98.17%的准确率。根据最新的报告显示,由我国燕山大学,四川大学,华北电力大学等联合提出的一种改进型的VGG16 神经网络模型,识别准确率高达99,97%,比起传统的识别模型,它的识别率更高,并具有很强的特征提取能力,可以做到识别与分类两项功能。尽管现如今的识别算法已经有很高的识别准确率,但是真正意义上的没有限制的手写体数字识别还有待进一步的提高。
1.4本文的研究内容及组织结构
传统意义上的特征提取和分类两个步骤的识别技术,需要人工设计方案来提取图像的特征,如图像的色彩特征、纹理特征等,这给识别技术带来了很大的工作量,并且图像提取器和分类器的性能直接影响了识别的最终结果。本课题从传统识别技术出发,借鉴学习当下热门的手写数字识别算法,提出了几种可行的聚类算法,可以在一定程度上提高识别的正确率。
本文对手写数字识别问题进行了简要概述以及意义阐明,并且对手写数字识别这项技术的发展和国内外研究状况进行了详细的介绍。在此基础之上,本文主要工作围绕着利用聚类算法处理手写数字识别的问题展开,通过建立相对应模型,完成对MNIST数据集的识别。
第一章为绪论。介绍了研究背景及意义、手写数字识别的国内外研究发展现状以及课题研究难点,并对本论文的研究内容以及论文组织结构进行了说明。
第二章为算法理论基础。本章重点介绍手写数字识别的三种聚类算法,并详细介绍算法中的相关技术细节。
第三章为识别算法实现。本章基于上一章所提到的聚类算法,进行手写数字识别的模型建立,并分析识别实现过程。
第四章为平台运行测试与结果。主要通过MATLAB平台,辅以Pycharm平台,对算法进行测试,并分析测试结果作简要分析。
第五章为总结与展望。对所有完成的工作进行总结,并对算法的进一步改进提出意见。
第2章 算法理论基础
所谓的监督算法,就是输入样本没有对应的输出或标签。而聚类算法则不同,它属于无监督学的习,因为在聚类中目标属性是不存在的,也就是说并不包含那些表示数据类别的分组或者分类信息。聚类(clustering)其实就是按照某个特定的准则(例如距离准则)把需要处理的数据集分割成不同的类别或簇,从而使得在统一类别或簇内的数据元素相似程度尽可能的大,同时不在同一类别或簇的s数据对象的差异性也尽可能地大,即确保聚类后同种类别的数据对象尽可能聚集在一起,不同的数据对象尽可能分离。
2.1 K-Means算法
在本章节的开头,我们提出了一种新的概念——“簇”。这是机器学习中给数据划分成为的不同类别的一种定义。若我们将一个具有M个样本的数据集划分成为K个簇,必然可以得到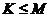 ,同时簇还满足以下几个条件:每个簇至少由一个数据对象构成;每个数据对象属于且仅仅属于一种簇;利用合理的聚类方法对上述条件的K个簇进行划分。下面我们就介绍聚类算法中最为基本的算法——K-Means算法。
,同时簇还满足以下几个条件:每个簇至少由一个数据对象构成;每个数据对象属于且仅仅属于一种簇;利用合理的聚类方法对上述条件的K个簇进行划分。下面我们就介绍聚类算法中最为基本的算法——K-Means算法。
- Means算法是一种基于划分的聚类算法,主要思想是:首先需要给定初始的类簇中心点设为K,随后将每一个数据对象划分到距离其最小的类簇中心点所在的类簇中,当所有的数据对象完成分配之后,根据某一个类簇内部所有的数据对象重新计算它的中心点(取平均值),然后通过不断的迭代、分配和更新的步骤,直到类簇的中心点变化非常小,或者迭代的次数达到设定的标准即可。
2.1.1基本原理
假定给定数据样本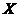 ,包含了
,包含了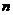 个对象X={
个对象X={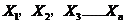 },其中每个对象都具有
},其中每个对象都具有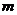 个维度的属性。K-Means算法的目标是将
个维度的属性。K-Means算法的目标是将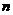 个对象依据对象间的相似性聚集到指定的K个类簇中,每个对象属于且仅属于一个其到类簇中心距离最小的类簇中。对于K-Means,首先需要初始化K个聚类中心,然后通过计算每一个对象到每一个聚类中心的欧式距离,如下式所示
个对象依据对象间的相似性聚集到指定的K个类簇中,每个对象属于且仅属于一个其到类簇中心距离最小的类簇中。对于K-Means,首先需要初始化K个聚类中心,然后通过计算每一个对象到每一个聚类中心的欧式距离,如下式所示
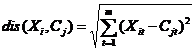
上式中,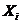 表示第
表示第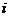 个对象(
个对象(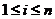 ),
),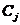 表示第
表示第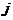 个聚类中心,
个聚类中心,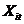 表示第
表示第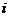 个对象的第
个对象的第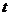 个属性,
个属性,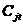 表示第
表示第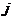 个聚类中心的第
个聚类中心的第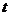 个属性。依次比较每一个对象到每一个聚类中心的距离,将对象分配到距离最近的聚类中心的类簇中,得到K个类簇。
个属性。依次比较每一个对象到每一个聚类中心的距离,将对象分配到距离最近的聚类中心的类簇中,得到K个类簇。
2.1.2算法流程
K-Means基本的算法流程主要由几个步骤完成:
- 首先我们需要从输入的数据集中随机地选取K个数据对象作为初始聚类的中心点,并由这个中心点来代表划分的各个聚类;
- 随后分别计算数据集合中各个数据对象到上述选取的K个中心点的距离大小,而后将数据对象划分到距离其最近的聚类中;
- 然后不断地对聚类中心进行调整,即使得聚类的中心与聚类的几何中心(平均值)相重合。这也是K-Means中mean的含义;
- 最后重复第二、第三步,直到聚类的中心不在漂移,此时算法收敛。
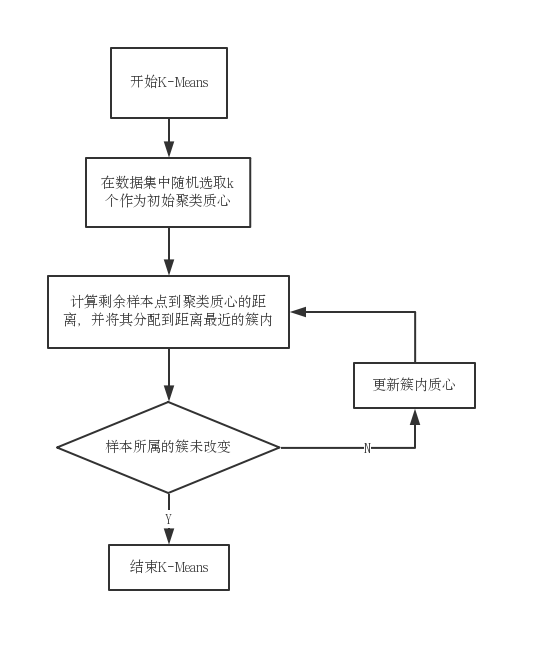
图2.1 K-Means算法流程图
K-Means聚类算法的本质就是在给定的集合元素距离计算方法的前提下,
不断进行聚类迭代和循环运算即可对元素进行聚类划分。由于其算法的基本流程比较的固定,所以在应用过程中,只需要定义合适的距离计算方法即可非常方便地将K-Means算法转化为计算机可执行程序进行上机运行,所以K-Means聚类算法目前而言是聚类算法中最为常用的算法。
由于K-Means算法对初选的K值是很敏感的,计算平均误差就是为了寻求最佳的K值。平均误差会随着K值的选取而改变,随着 K值增大,平均误差会逐渐降低;极限的情况下是每个样本点都是一个类,这时的平均误差E=0,当然这种聚类是没有任何研究价值的。那么哪个K值是最佳选择成为K均值算法的核心问题,这里运用的方法为Elbow method——也就是“肘”方法。对于n个数据集,迭代计算k从1到n,每次聚类完成以后再计算每个点到其所属的簇中心的距离的平方和,可以想象到这个平方和会逐渐变小,知道k无限趋紧于n时,平方和变为0,因为每个点都是它所在簇中心本身。但是在这个平方和变化的过程中,会出现一个拐点也即“肘”点,下图可以看到下降突然变缓时即认为是最佳k值。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: