偏振光在YVO4单轴晶体界面的传输情况分析毕业论文
2020-02-17 22:32:49
摘 要
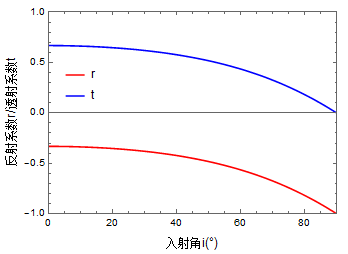
本论文主要基于晶体的双折射效应和电磁场边界条件,利用麦克斯韦方程组和物质方程分析了寻常光和非寻常光在正单轴晶体YVO4界面上折射特性及反射损耗损耗与偏振态变化。
主要工作为:给出任意光轴取向时非寻常光从各向同性介质入射YVO4晶体时的折射方程,得出光轴在入射面内时e光的折射情况;确定入射e光和光轴在法线同侧的一定范围内产生负折射现象,最大入射角为12.8559°,最大负折射角为-6.0531°;利用菲涅耳公式,分析光轴在入射面内时o光和e光在各向同性介质与YVO4晶体交界面和两个单轴晶体交界面的反射率和透射率,分析入射角和光轴角对反射损耗的影响,得出实现零损耗传输时的入射角和光轴角。
结果表明,光轴角会影响负折射角;o光在YVO4晶体界面反射损耗不为零且随入射角增大而增大,e光在空气与YVO4晶体界面入射角为62.5269°时反射损耗为零,在两个光轴方向相同或对称的YVO4晶体界面反射损耗为零。e光反射率为零即对应折射偏振光中e光比例增加,可用于起偏或者偏振度控制。
本文的特色是从公式出发,利用mathematica软件对折射特性和反射率(透射率)进行数值和作图分析,并分析变量之间的依赖关系和特殊情况的值和范围。
关键词:YVO4晶体;折射特性;反射率;透射率
Abstract
Based on the birefringence effect of the crystal and the boundary conditions of the electromagnetic field, the dissipative properties and the reflection loss and polarization state change of the ordinary light and the extraordinary light at the YVO4 interface of the positive uniaxial crystal are analyzed by Maxwell's equations and material equations.
The main work is: giving the refraction equation of extraordinary light on the YVO4 crystal from the isotropic medium when the optical axis is arbitrary, and obtaining the refraction of the e-light when the optical axis is in the incident plane.determining the incident e-light and the optical axis in a certain range on the same side, the Negative Refraction occurs . the maximum incident angle is 12.8559°, and the maximum negative refraction angle is -6.0531°. Using the Fresnel formula, the o-light and e-light are suitable when the optical axis is in the incident plane. The reflectivity and transmittance of the interface between the isotropic medium and the YVO4 crystal and the interface between the two uniaxial crystals are analyzed. The influence of the incident angle and the optical axis angle on the reflection loss is analyzed, and the incident angle and the optical axis angle at the time of zero loss transmission are obtained.
The results show that the optical axis angle affects the negative refraction angle,the reflection loss of the o-light at the YVO4 crystal interface is not zero and increases with the incident angle. The reflection loss of the e-light at the surface of air and YVO4 crystal is 0 when the interface angle is 62.5269°. The reflection loss at the interface of the YVO4 crystal which is the same or symmetric in the two optical axes is zero. The e-light reflectance is zero, that is, the proportion of e-light in the corresponding refracted polarized light is increased, and it can be used for polarization or polarization degree control.
The characteristics of this paper are to use the mathematica software to perform numerical and graph analysis of refractive properties and reflectivity (transmittance), and to analyze the dependence between variables and the value and range of special cases.
Key Words:YVO4 crystal;refraction property;reflectivity;transmissivity
目 录
第1章 绪论 1
1.1 负折射研究进展 1
1.2 YVO4晶体及应用 2
1.3 本文研究目的和内容 2
第2章 YVO4晶体折射特性 4
2.1 单轴晶体及双折射 4
2.2 折射角公式 7
2.2.1 o光折射角公式 7
2.2.2 e光折射角公式 7
2.3 YVO4晶体折射 10
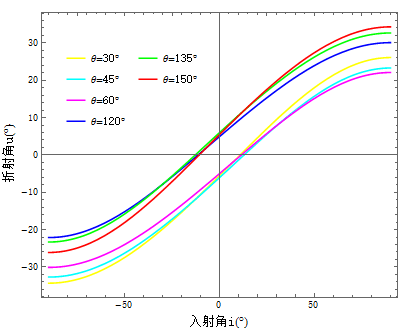
2.3.1 e光折射角分析 11
2.3.2 负折射入射角范围 13
2.3.3 负折射折射角范围 15
第3章 YVO4晶体反射率与透射率 16
3.1 单轴晶体界面上的菲涅耳公式 16
3.2 o光反射率与透射率的计算 18
3.3 e光反射率与透射率的计算 20
3.3.1 空气与YVO4晶体界面的反射率和透射率 20
3.3.2 两单轴晶体界面的反射率和透射率 24
3.4 偏振光传输后的能量损耗和偏振态变化 30
3.4.1 能量损耗 30
3.4.2 偏振态的变化 31
第4章 结论 33
参考文献 34
致 谢 36
第1章 绪论
1.1 负折射研究进展
负折射在上世纪60年代被理论预言,到几十年后首次才在实验中被观测到,因负折射有与正常折射有相反的性质,对负折射的研究及应用也越来越多。人们到目前为止,只在以下三种情况下观察到了负折射现象:1.在由一些金属环和棒所构造出的负折射材料(左手材料)的界面处;2.在光子晶体的界面处;3.在各向异性晶体的界面处[1]。2001年,DavidSmith等教授利用铜复合材料首次制造出有负介电常数和负磁导率的在微波波段物质,并且观察到了其中的负折射现象。2003年,S.Foteinop- oulou教授在爱德华州立大学发布了关于光子晶体负折射理论的仿真和研究结果。之后具有负折射率的介质在各个光波段都被证实,现阶段对负折射率材料的研究已经能够运用到信息量的存储、移动通信电磁吸收隐身等诸多军用或民用领域[2]。直到2004年,Liu等人发现了光束从各向同性介质入射到单轴晶体也会出现负折射现象,并对单轴晶体的负折射现象进行了分析,并且得出要实现晶体负折射现象的入射角范围,近年关于负折射的研究主要集中在各种新型负折射率超材料(如等离子体)中的负折射现象[3-5]。然而并不能直接在自然界中得到负折射率物质和光子晶体,并且光子晶体比普通单轴晶体难加工,而所有各向异性晶体都可产生负折射[3],与左手材料和光子晶体中所观察到的负折射也有着本质上的差别,对各向异性晶体负折射的研究和应用有很大的前景。
在单轴晶体界面产生的负折射现象,是因为入射角在一定范围内时光束能流发生了负折射,而不是单轴晶体本身具有负的介电常数和磁导率,因为单轴晶体的主折射率均都是正值[6]。单轴晶体的负折射现象来源与单轴晶体各向异性性质,与负折射率材料中出现的负折射现象本质完全不同。虽然利用负折射率材料的负折射能够实现完美透镜的效果,让大角度入射的光线经材料后完美会聚与一点,而无像差。但在单轴晶体负折射只有入射角在一定的范围内才会出现[7],大角度入射的光束不能聚焦,光束传输在单轴晶体中传会出现像差,故单轴晶体不能做成完美透镜[8]。尽管如此,单轴晶体负折射现象在理论上依旧能够运用于很多光学器件,实现光束的偏折,对单轴晶体负折射的应用价值依旧值得深入研究。图1.1为负折射现象的演示图,其中入射光线和折射光线在法线同侧,利用负折射能够实现与正折射完全不同的光线偏折。
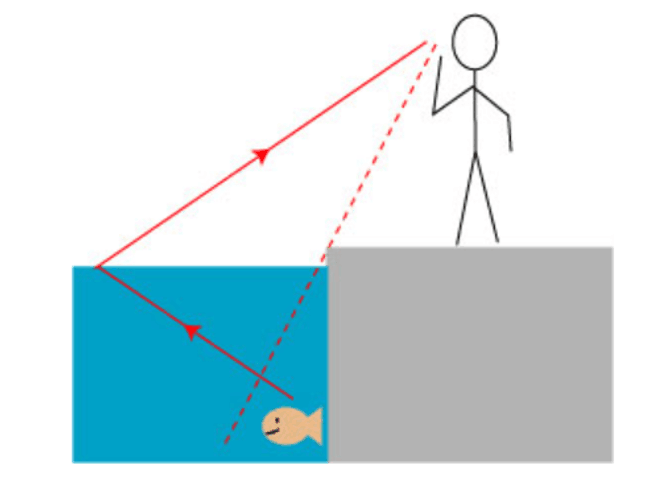
图1.1 负折射现象
1.2 YVO4晶体及应用
近年来新开发了一直非常良好的双折射晶体—YVO4晶体,该晶体是一种正单轴晶体,且在可见光附近波段范围内具有很好的透光性,透光光谱范围为0.4um-5um,且其机械物理性能强和温度稳定性好,相比于其他双折射晶体且有较大的主折射率值和双折射率差。相比于与其他常用的双折射晶体,和方解石相比,方解石易潮解、硬度较低,光学特性较差,而YVO4晶体硬度高,机械加工性能好,且不溶于水;与金红石相比,金红石偏硬,而YVO4较易加工,成本低,适用于大批量生产;与铌酸锂晶体相比,虽然两种晶体具有很相似的物理特性和机械特性,但YVO4的主折射率差是铌酸锂晶体主折射率差的三倍以上。YVO4晶体的这些优良特性使其在近年来迅速的成为了有非常良好的应用前景的双折射材料,并已经开始广泛的应用于光电产业中。
双折射现象指一束光一定条件下在各向异性晶体界面发生折射时,将会产生两束折射光[9]。而YVO4晶体由于具有非常良好的双折射晶体,现在主要应用于在各种分光和偏光光学器件上,如光环形器、光隔离器、光分束器、偏光器等,尤其是双折射效应应用于医学、应力诱导双折射和光纤技术中[10]。同时,对YVO4晶体掺入相关激光器增益介质可组成效率很高的固体激光器,其发射截面大,有大的吸收带宽和吸收效率[11]。虽然所有的各向异性介质都可表现出双折射特性,但是只有双折射率(|no-ne|)较大的介质表现出来的双折射现象更明显,故YVO4晶体在光学器件领域具有很好的应用前景,YVO4晶体折射特性与零损耗条件能够为其作为波导、分光偏光元件和环形器等应用提供理论依据。
1.3 本文研究目的和内容
在使用晶体制作光学器件时,都会涉及光在晶体界面上的入射与出射问题,因此需要考虑光从空气入射晶体界面,或由晶体内部入射另一晶体界面时的反射与透射特性[12]。
本文研究目的为:推导YVO4晶体界面上o光和e光折射角公式,获得特定光轴角度时晶体的折射和分光情况,分析o光和e光在YVO4晶体界面的反射损耗,确定零损耗条件,以便设计晶体偏光或分光应用中所需的条件。
本文主要研究内容为:o光和e光从各向同性介质入射到YVO4晶体的折射特性,包括o光折射角公式,光轴方向任意(光轴在入射面内和不在入射面内情况)时e光光线折射角关于光轴方向角和入射角公式,分析光轴平行入射面和垂直入射面情况下折射角,利用软件得出折射角与光轴角和入射角关系,由折射率公式可求得产生负折射入射角范围和负折射角范围。推导单轴晶体界面的菲涅耳反射和透射公式,分析o光e光由空气入射到YVO4晶体界面的反射系数(率)、透射系数(率),分析e光反射率为零时条件,进一步分析当两光轴都在入射面内时偏振光由一单轴晶体入射到另一单轴晶体时的反射率和透射率,确定零损耗条件和偏振态的变化。根据研究得出的折射特性分析正单轴晶体YVO4晶体作为波导的实际应用,折射特性对其的影响,得出最佳条件。
YVO4晶体折射特性
2.1 单轴晶体及双折射
单轴晶体只有一个光轴,当入射光束沿着光轴方向传播时不会发生双折射现象,单轴晶体的主相对介电系数为
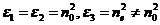 (2.1)
(2.1)
且称主折射率negt;no的晶体为正单轴晶体,称主折射率nelt;no的晶体为负单轴晶体[12]。
一束单色平面入射光在各向异性晶体界面上会产生两束折射光,这就是双折射现象。在晶体内,这两束光分别被称为o光(寻常光)与e光(非寻常光),o光的折射服从折射定律,而e光的折射则不遵从折射定律,o光和e光都是线偏振光,且它们的偏振方向互相垂直[12]。
从麦克斯韦方程组出发,分析光波在晶体中的双折射现象,若各向异性介质晶体均不导电、非磁性,且晶体中不存在自由电荷,则麦克斯韦方程组可表示为
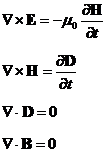 (2.2)
(2.2)
对于各向异性晶体,电位移矢量D和电场矢量E方向不相同,故物质方程为
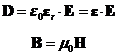 (2.3)
(2.3)
单色平面光波方程为[13]
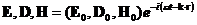 (2.4)
(2.4)
将(2.3)式和(2.4)式带入(2.2)式,化简得
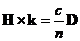 (2.5)
(2.5)
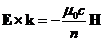 (2.6)
(2.6)
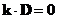 (2.7)
(2.7)
 (2.8)
(2.8)
其中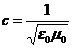 ,
,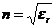 ,k为波法线单位向量。 由(2.7)式和(2.8)式可知,k和D都与H矢量垂直,k和E都与H垂直,所以E、D、k在垂直于H矢量的平面内,并且D
,k为波法线单位向量。 由(2.7)式和(2.8)式可知,k和D都与H矢量垂直,k和E都与H垂直,所以E、D、k在垂直于H矢量的平面内,并且D
矢量和E矢量在一般情况下不同向[12],如图2.1为单轴晶体中e光示意图。
![MTXMF0SX25%3S1~]N%NZ6~S](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw1659_2020217223243417.png)
图2.1 单轴晶体中的e光
图中光波法线k与光轴夹角为μ,e光光线与光轴夹角为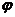 ,光波与光线离散角为α。
,光波与光线离散角为α。
联立(2.5)式和(2.6)式,消去H,可以得到
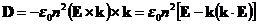 (2.9)
(2.9)
将(2.8)式写成分量形式
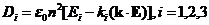 (2.10)
(2.10)
将(2.2)式代入(2.9)式,整理可得
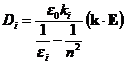 (2.11)
(2.11)
将(2.11)式代入(2.7)式后可得
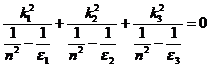 (2.12)
(2.12)
因为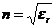 ,所以上式也即
,所以上式也即
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
![QFPO]TGZRZ67$H9ZYXY0YAQ](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw1659_2020217223243877.png)
![TQ2N9MMCAHKA5M@X]86Q99W](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw1659_2020217223244640.png)
![`3@E@]25HC9MTQCA}TTY[MJ](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw1659_2020217223244856.png)
![AXYA%J5EELCD9X]0OLGPOPD](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw1659_2020217223245185.png)
![0T{NC]%%FMID89D9DMVPL`V](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw1659_2020217223245358.png)