摘 要

金属薄膜材料是利用蒸发法、溅射法或者化学气相沉积法，在基底表面沉积或制备的物理层。它的光学性质与体材料光学性质截然不同，薄膜厚度降低至纳米级时，就会出现的全新物理特性。尤其在膜厚度低于30nm时，其折射率随厚度变化更加剧烈，了解其变化的趋势，就能更好的理解金属薄膜的微观介电性能。所以本文利用椭圆偏振法测量厚度低于30纳米的金属薄膜的折射率和介电常数，通过结果分析讨论其折射率与厚度的关系。主要工作内容包括：

1. 对椭圆偏振法的机理进行理论分析与仿真计算，理解并掌握椭圆偏振法测薄膜厚度和折射率的基本原理；
2. 建立膜厚度与介电常数和折射率的理论分析模型，找出膜厚度改变时可能影响介电常数和折射率的所有因素；
3. 在相同条件下制备不同厚度的金属薄膜，通过椭圆偏振法测量其厚度、介电常数和折射率。通过所得结果分析折射率和介电常数随膜厚的变化趋势，并分析其影响因素。

实验结果表明金膜的折射率随厚度的减小而增大，介电常数的实部和虚部都会随着薄膜厚度的减小而增大，并且厚度越薄，其折射率和介电常数变化就越大。

关键词：超薄贵金属薄膜；椭圆偏振法；折射率；介电常数

Abstract

The metal thin film material is a physical layer deposited or prepared on the surface of the substrate by an evaporation method, a sputtering method, or a chemical vapor deposition method. Its optical properties are very different from those of bulk materials. When the film thickness is reduced to the nanometer level, new physical properties appear. Especially when the film thickness is less than 30nm, the refractive index changes more sharply with thickness, and the change trend of the film can better understand the microscopic dielectric properties of the metal film. Therefore, the refractive index and dielectric constant of metal films with thickness less than 30 nm are measured by ellipsometry. The relationship between refractive index and thickness is discussed by the results. The main work includes:

1. Theoretical analysis and simulation calculation of the mechanism of ellipsometry; understand and master the basic principle of ellipsometry to measure film thickness and refractive index;

2. Establish a theoretical analysis model of film thickness and dielectric constant and refractive index to find out all the factors that may affect the dielectric constant and refractive index when the film thickness changes;

3. Metal films of different thicknesses were prepared under the same conditions, and their thickness, dielectric constant and refractive index were measured by ellipsometry. The results show that the refractive index and dielectric constant change with the film thickness, and analyze the influencing factors.

The experimental results show that the refractive index of the gold film increases with the decrease of the thickness. The real and imaginary parts of the dielectric constant increase with the decrease of the film thickness, and the thinner the thickness, the refractive index and dielectric constant. The change is greater.

Key words: ultra-thin precious metal film; ellipsometry; refractive index; dielectric constant

目 录

第一章 绪论 1

1.1 贵金属纳米薄膜的折射率特性 1

1.2 金属薄膜的制备与检测方法 1

1.2.1 金属薄膜材料的制备 1

1.2.2 金属薄膜折射率的检测 2

1.3 论文的研究内容与章节安排 3

第二章 椭圆偏振法传感模型和介电常数仿真 4

2.1 椭圆偏振法的传感模型 4

2.2 介电常数模型的建立 6

2.2.1介电常数与厚度的关联模型 7

2.3 贵金属薄膜介电常数仿真 8

2.4 本章小结 11

第三章 椭偏仪测量超薄贵金属薄膜折射率实验 12

3.1 超薄贵金属薄膜制备 12

3.1.1 镀膜准备 12

3.1.2 利用磁控溅射镀膜机镀膜 12

3.2 椭偏仪测超薄贵金属薄膜 14

3.2.1 椭偏仪实验系统 14

3.2.2 超薄贵金属薄膜折射率的测定 15

3.2.3 实验结果与误差分析 15

3.3 本章小结 19

第四章 总结与展望 20

参考文献 22

致谢 24

第一章 绪论

1.1 贵金属纳米薄膜的折射率特性

贵金属纳米薄膜材料是一种光学性质与体材料存在不同的材料，当这种薄膜材料的厚度减少到纳米级时，它会显现出原来没有的全新的物理现象。这使得纳米级的金属薄膜材料的研究成为了研究热点。许多学者对超薄贵金属材料的研究，都旨在研究它的介电性能，希望借此让这种材料在微电子领域得到更广泛的应用。而有关超薄贵金属薄膜的光学性能尤其是有关超薄贵金属薄膜折射率的研究尤为稀少。而由于金属薄膜材料的光学性能具有其它薄膜材料不可替代的优越性，因此在光电器件中有着广阔的应用空间^[1]。这使得对于金属薄膜材料的光学性质的研究显得十分重要。

纳米级金属薄膜的折射率会随着厚度的减小而发生突变，尤其在30nm以下这种变化显得尤为明显。造成这种现象的主要原因是当金属薄膜厚度小于其电子的平均自由程时，其电导率和折射率会因为尺寸效应和体积效应而发生巨变。本文旨在研究30nm以下的贵金属薄膜材料的折射率与其厚度的关系。

1.2 金属薄膜的制备与检测方法

以下是几种最通用的制备和测量金属薄膜折射率的方法。通过比较这些方法，选择出合适的制备与检测方法。

1.2.1 金属薄膜材料的制备

金属薄膜的厚度一般在零点几纳米至几十纳米之间。大约是几个原子层至几百个原子层的厚度^[2]。制备金属薄膜的方法有很多，这些方法总体上可分为两个大类：化学方法和物理方法。化学方法包括：化学气相沉积法^[3]、电镀法^[4]等。物理方法包括：真空热蒸发法^[5]、磁控溅射法^[6]等。金属薄膜材料的光学常数与制备方法和制备工艺息息相关，优异的制备方法制备出的金属薄膜更具有测量的意义。下面主要介绍这制备薄膜的物理方法，并比较它们的优缺点。

真空热蒸发法属于物理气相沉积方法。它是一种将固体材料也就是靶材料置于高真空环境中加热，使之升华或蒸发，借此沉积在基底上获得薄膜材料的方法。它具有设备简单、易操作、成膜质量和成膜速率快的优点。一般用于给熔点不高且对成膜质量要求不高的材料镀膜。这种方法最大的缺点就是成膜质量不高，所成薄膜与基底的粘附性较差，尤其是非常薄的薄膜。本实验需要制备30纳米以下的薄膜。为了实验结果的准确性。故不选用此方法。

磁控溅射法也属于物理气相沉积法。这种方法将涂层材料做为阴极，利用氩原子轰击靶材，产生溅射，再通过磁场和电场控制，使更多的靶材粒子溅射到基底上形成沉积层。磁控溅射法具有很高的成膜速度，因此这种方法被广泛应用于工业镀膜中。而且用这种方法制备的薄膜与衬底有很强的粘附性，并能制备热蒸发法不能制备的高熔点，低蒸气压的物质膜。成膜的质量和连续性较好，表面粗糙度也较低。十分符合本实验的薄膜需求。故选用此方法镀膜。

近年来，随着科技的发展，国内外对真空热蒸发法和磁控溅射法的研究也取得了一定的进步。对于真空热蒸发法，需要解决的主要问题是加热器的寿命问题。国内外已采用寿命较长的氮化硼合成的导电陶瓷材料作为加热器，来提高加热器的寿命。在日本甚至有使用特殊材料的坩埚，可以大大提高加热器的寿命。而对于磁控溅射法，自上世纪70年代该技术问世以来，就取得了迅速的发展。近年来，随着计算机技术的发展，磁控溅射镀膜机也朝着自动化，智能化的方向发展。在应用方面，真空热蒸发法一直被用来制作熔点不高的金属薄膜，比如国内的唐秀凤教授就采用了真空热蒸发法在ITO基底上制备WO3薄膜^[7]。而磁控溅射法一般用于贵金属薄膜的制备，比如武秉晖教授就采用了直流磁控溅射法在烧结钕铁硼磁极表面镀覆不同厚度的Tb膜^[8]。磁控溅射法制备的薄膜在质量上要明显优于真空热蒸发法。

1.2.2 金属薄膜折射率的检测

金属薄膜材料的折射率是金属薄膜材料的光学常数之一，它是金属薄膜材料的光学性能的重要表征。因此准确测量金属薄膜材料的折射率对我们分析金属薄膜的光学性质有重大意义。测量技术不断改进，测量的精度也就逐步提高。在这期间有不少优异的测量方法问世。比如椭圆偏振法、棱镜耦合法和干涉法。他们各有各的优点与不足。下面就简要介绍这几种常用的测量金属薄膜折射率的方法。

椭圆偏振法是利用一束入射光照射样品表面，通过检测和分析入射光和反射光偏振状态从而获得薄膜厚度及其折射率的非接触测量方法^[9]。它的厚度和折射率的重复性精度十分之高，分别可以达到0.01纳米和万分之一。而且适用的材料非常之多，比如半导体、金属薄膜和具有多层膜结构的材料。这种方法还是一种无损测量方法，不会在测量时对待测膜产生损耗。但是，具有较高精度的椭偏仪设备结构复杂，操作不易上手，价格昂贵，其实验数据的处理过程十分漫长而繁琐，而且其实验结果的准确性还与实验者十分能熟练操作仪器有关。本次实验对实验精度有很高的要求，所以本次实验才使用这种方法测目标金属薄膜的折射率和厚度。而且椭偏仪测超薄薄膜的已经有了许多国内外的研究，例如Sarah M. Eichfeld用椭圆偏振法快速测定超薄WSe₂、Chanyoung Yim用椭圆偏振法研究二氧化硅薄膜的光学性质和Hsiang-Lin Liu用椭圆分光光度法研究单层过渡金属双卤代烃的光学性质。他们的文章都提到了椭圆偏振仪快速，高效和不会破坏薄膜本身的优点。

棱镜耦合法利用了光学隧道效应，它通过在待测薄膜表面摆放一组耦合棱镜，使入射光照射到需要测量的薄膜上，通过测量和处理不同入射角的反射光来判断波导耦合角，再通过波导耦合角来求解被测薄膜厚度和折射率。由于需要在膜表面摆放棱镜，可能会对待测膜造成损耗。这种方法的精度很高，折射率精度可达千分之一。现在市面上也有全自动化的棱镜耦合测量仪，但由于容易对膜表面造成不可逆转的损耗，所以本次实验不用此方法。近年来，棱镜耦合法一般用来测复合材料的折射率，比如杨天新教授的棱镜耦合法确定条形波导的渐变折射率分布的研究中就使用了棱镜耦合法来测量条形波导样品的折射率^[10]。

干涉法使利用等厚干涉条纹来测量薄膜折射率和厚度的一种方法。这种方法所使用的设备简单，操作方便，计算简单。由于这种方法需要判别条纹错位量，测量精度往往不高。但本次实验要测得膜都非常薄，都低于30纳米。所以不宜采用此方法。近年来，干涉法一般用来测量液体或气体的折射率。比如国内的高旭教授就采用了极管干涉法设计了一个液体折射率测量的光学系统^[11]。

1.3 论文的研究内容与章节安排

本次研究课题的目的在于利用椭圆偏振法测量由磁控溅射镀膜机制备的超薄纳米金属薄膜的光学常数，通过实验结果分析讨论光学常数与厚度的关系。实验方法是利用磁控溅射镀膜机制备不同厚度的薄膜，再用椭圆偏振法确定薄膜厚度和折射率，最后将数据进行处理，探讨折射率和厚度的关联与内在因素。

章节安排：

第二章进一步阐述椭圆偏振法测定薄膜厚度和折射率的基本原理，并建立介电常数模型，利用matlab仿真从理论上探讨金属薄膜变薄对其光学常数尤其使折射率的影响；

第三章是实验部分，先用磁控溅射镀膜机来制备实验所用的金属薄膜；再通过椭偏仪测量薄膜的厚度和折射率，得到实验数据；最后处理实验结果并分析实验误差；

第四章是总结与展望。

第二章 椭圆偏振法传感模型和介电常数仿真

2.1 椭圆偏振法的传感模型

实验室中的椭偏仪有两种测量模式：反射模式和透射模式^[12]。它们测量薄膜的原理都是根据入射光经过待测薄膜表面反射或透射后，出射光对于入射光来说发生的偏振态的变化来确定薄膜的厚度和光学参数。

在椭偏仪反射测量模式^[13]中，入射光以一定的入射角入射到待测薄膜上。待测薄膜对于入射光的电场分量E_p(平行于入射光)和E_s(垂直于入射光)有着不同的透射和反射系数，经待测膜反射后的出射光在偏振态上一定会发生变化。我们就可以根据这种变化来确定薄膜的厚度和光学参数。入射光在单层的金属薄膜表面的反射如图2.1所示。

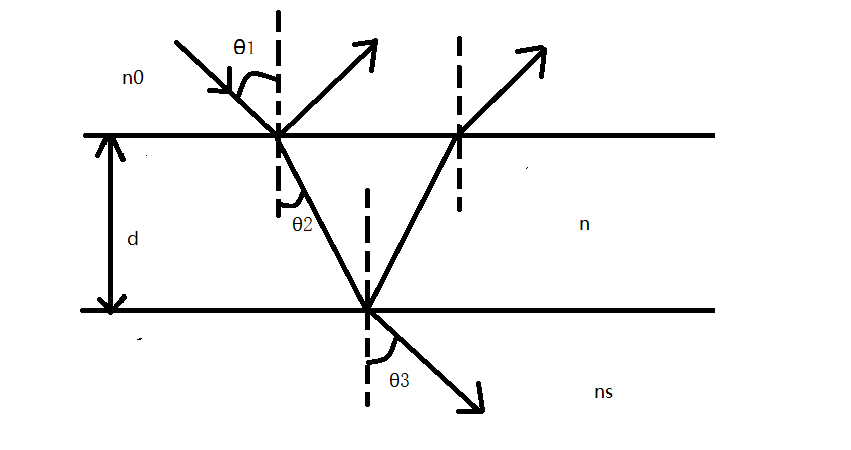
图2.1 偏振光在单层膜上的反射示意图

如图2.1所示，n₀、n和n_S分别表示空气、待测薄膜和衬底材料的折射率；θ₁、θ₂、θ₃ 分别表示从空气入射到薄膜的入射角，光线在薄膜中的折射角，从薄膜入射到衬底材料的折射角。当入射光以入射角θ₁从空气中入射到待测薄膜上时，入射光在薄膜的上下表面发生了多次反射和折射。每次反射和折射后，光的振幅和相位都会发生变化。

根据相位差公式

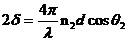（2. 1）

和菲涅尔公式

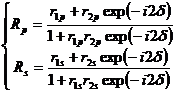（2. 2）

得到反射系数比ρ

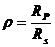（2. 3）

其中，λ为真空中光的波长；r_1p，r_1s，r_2p，r_2s分别表示P分量和S分量在薄膜上表面和下表面上进行一次反射的反射系数。

由（2.1）~（2.3）式可得：

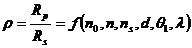（2. 4）

通过求解上面的方程可以求出复指数X的值进而求解出薄膜的厚度d：

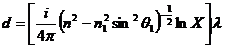（2.5）

由上述原理可以看出，要想求薄膜的厚度和折射率必须得到入射光和反射光的反射系数比ρ，而反射系数比ρ不能直接求出，我们要引入两个重要的参数ψ和Δ^[14]。他们与ρ的关系如下：

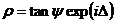（2. 6）

（2. 7）

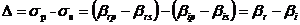（2. 8）

ψ和Δ是椭偏参数。它们具有实际的物理意义：ψ的正切表示光经过薄膜表面反射前后P分量和S分量的振幅的衰减比；而Δ表示P分量和S分量的位移之差^[15]。这两个参数可以直观地反映入射光经薄膜反射前后偏振态发生了怎样的变化。而且这两个参数都可以从实验中测出。这就表明在一定条件下，只要能从实验中测得这两个椭偏参数，就可以得到薄膜的厚度和折射率。

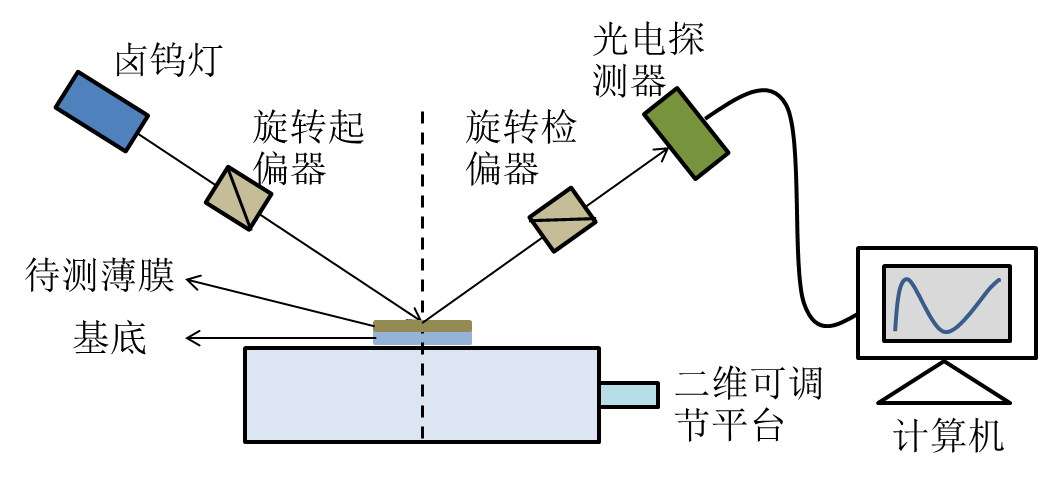
椭圆偏振法测量薄膜厚度的系统如下图所示。

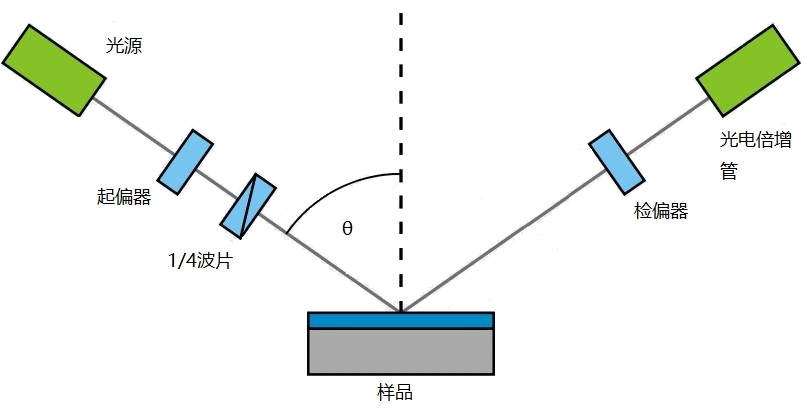
图2. 2 椭圆偏振法测薄膜厚度系统示意图

系统中需要测量的量有起偏器的方位角P和检偏器的方位角A。它们与椭偏参数ψ和Δ有如下关系。

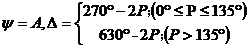（2. 9）

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：