摘 要

热固性树脂基复合材料热压成型的过程较为复杂,确定合理的工艺参数决定着制件的质量，也直接影响着生产成本。传统工艺通常采用做试验摸索的方法,也就导致了材料研制周期较长、成本较高和可靠性低等问题,制约着热固性树脂基复合材料的实际应用。近年来由于数字技术的快速发展,通过建立数字模型、进行数值模拟大大减少了制造成本以及研制时间，是目前研制树脂基复合材料低成本、高质量的一种较高效的方法。

本文基于有效应力准则与达西定律建立了厚L形复合材料层合板流动压实数值模型，通过建立复合材料平板模型，计算结果与实验数据对比，验证了模型的正确性。运用欧拉流线方程建立了符合L形复合材料层合板模型的曲线坐标系，利用Comsol软件进行计算分析，分析了厚L形复合材料平流动压实固化行为，分析了复合材料流动压实行为对纤维体积分数与有效应力的影响。

关键词：复合材料；L形构件；流动压实；有限元

Abstract

The process of hot pressing molding of thermosetting resin matrix composites is complicated. Reasonable process parameters determines the quality of the workpiece, and also directly affects the production cost. Traditional processes usually use the method of experiment and exploration, which leads to the problems of long material development cycle, high cost and low reliability.It restricts the practical application of thermosetting resin matrix composites. In recent years, due to the rapid development of digital technology, the establishment of digital model, numerical simulation has greatly reduced manufacturing costs and development time, is currently the development of resin matrix composites low cost, high quality of a more efficient method.

This paper is based on the effective stress criterion and Darcy's law.In this paper, a numerical model of flow compaction of thick L-shaped composite laminates is established, and the correctness of the model is verified by establishing the composite plate model and comparing the calculated results with the experimental data. It uses Euler flow equation to establish a curve coordinate system, which conforms to the model of L-shaped composite laminated plate, and the calculation and analysis of the flat flow compaction of thick L-shaped composites are analyzed by using Comsol software, and the influence of composite flow pressure on fiber volume fraction and effective stress is analyzed.

Keywords:Composites; L-shaped components; Flow compaction; Finite element

目录

第1章 绪论 1

1.1 背景介绍 1

1.2 国内外研究现状 1

1.2.1 流动-压实研究 2

1.2.2固化过程研究 2

1.3 本文研究内容 3

第2章 热固性复合材料流动压实固化模型及验证 4

2.1 热-化学模型 4

2.2 固化反应模型 5

2.3 流动压实模型 5

2.4 树脂粘度模型 6

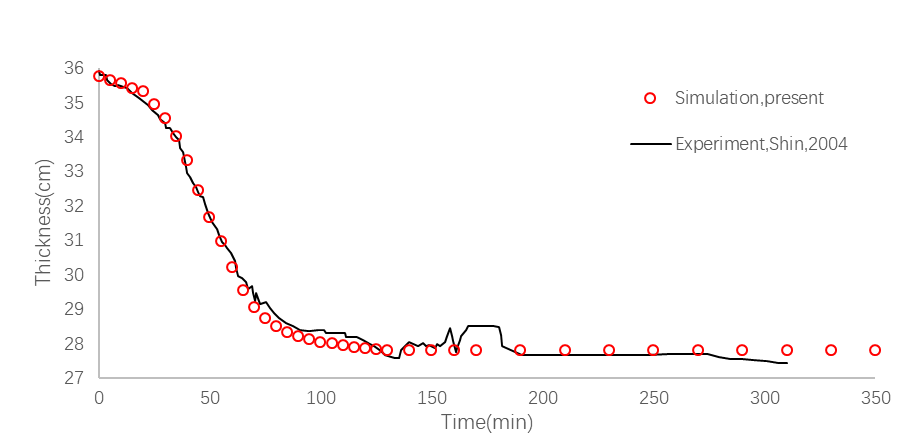
2.5 模型验证 7

2.6 平板流动压实行为分析 9

2.7本章小结 11

第3章 L形单向板构件固化流动-压实行为分析 12

3.1 数值分析模型 12

3.2 曲线坐标系的构建 13

3.3 结果分析 14

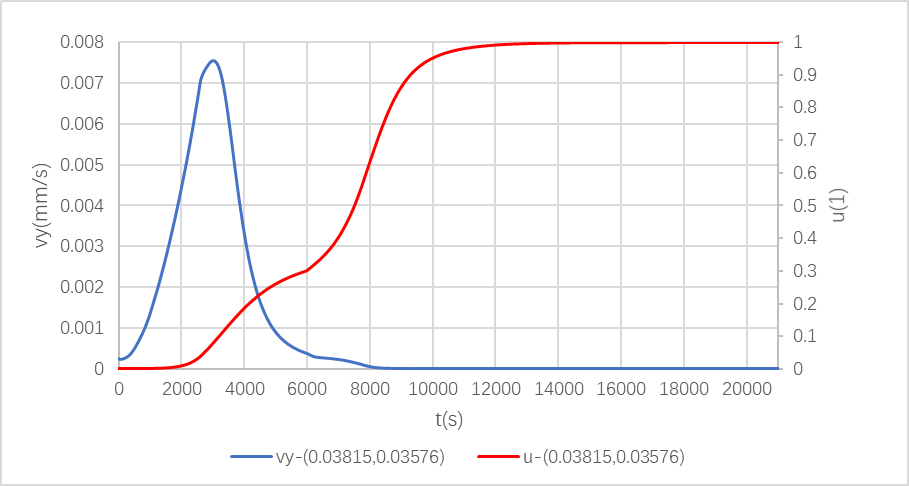
3.3.1 变形分析 14

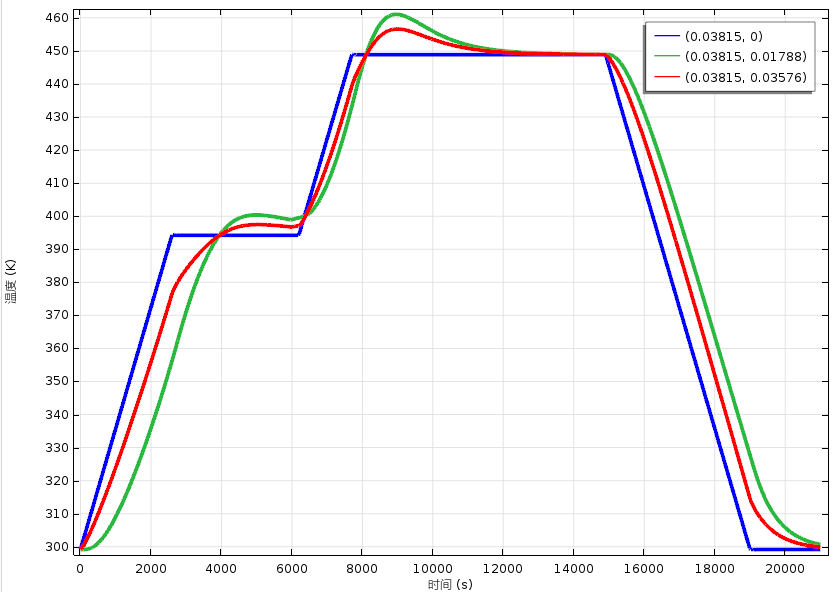
3.3.2 固化度、温度及粘度分析 15

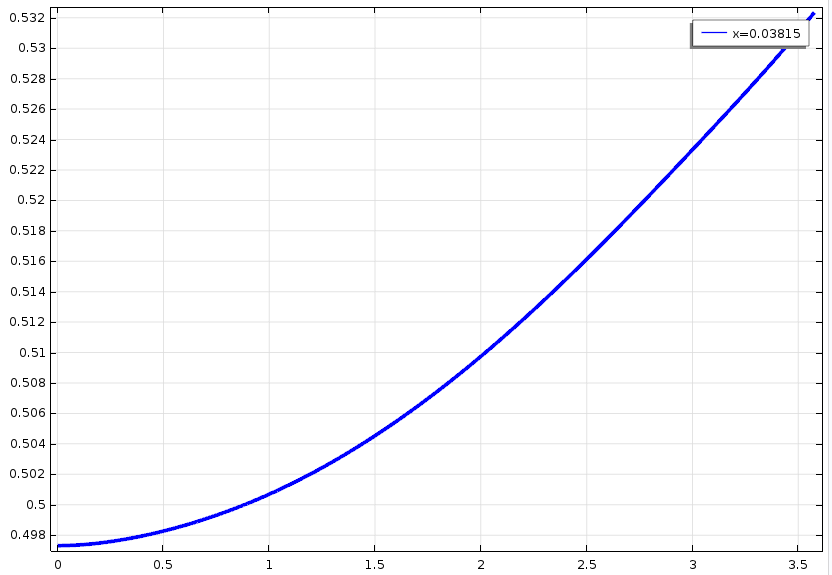
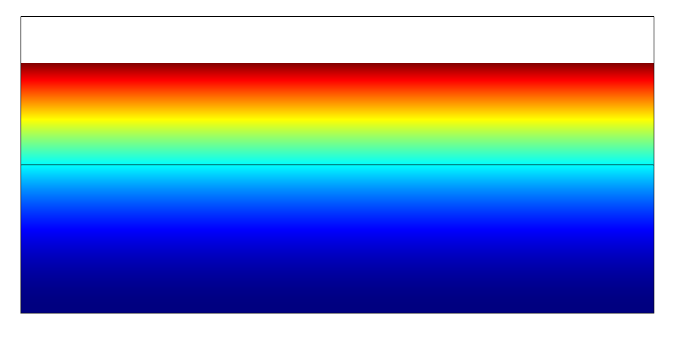
3.3.3 纤维体积分数与有效应力分析 17

3.4 本章小结 20

第4章 总结与展望 21

4.1 总结 21

4.2 展望 21

参考文献 22

致 谢 24

第1章 绪论

1.1 背景介绍

热压固化成型是生产最终形状的纤维增强聚合物部件的过程。为了设计合理的固化工艺提高产品质量，热压成型处理的数值模拟和优化已经在工业中得到广泛应用。在固化过程中，根据预定的温度周期加热，同时根据预定的压力周期加压。当树脂粘度变得足够低时，施加的压力将多余的树脂从复合材料挤压至吸胶层，同时纤维床被逐渐压实。施加的热量增加了复合材料的温度，导致固化过程的发展，树脂粘度会相应地的变化。

复合材料固化过程模拟使用基于物理的模型来模拟，并预测固化过程中各物理-化学参数的演化。例如纤维体积分数，树脂压力，厚度，固化度，温度等性质。

由于固化周期对层压复合材料的质量有很大程度的影响，因此为每种应用选择固化周期很重要，必须进行优化。因此，为了适当地为每种应用选择合适的参数，必须采用固化过程的一些基本模型并进行优化。

纤维增强复合材料在一级结构中的应用前景在一定程度上取决于构件的制造是否经济高效。航空航天复合材料的材料成本大约是目前使用的铝材料的十倍。但是，复合材料能够制造出形状复杂、紧固件和零件较少的大型结构板。对于这些类型的结构, 不同的结构元素, 如表面, 框架和加固件的制造仅在一次制造工艺中完成, 大大降低了制造成本。因此，可以通过减少与组装结构部件相关的劳动力和其他成本来补偿材料的较高成本。是否能够完成成本的控制，完全取决于是否能够提供一个良好的制造工艺的设计。这样的工艺应该产生出满足设计公差的高质量结构, 因为大型主要结构的拒绝成本相当高。如今, 大型复合材料部件通常都是以高品质为目标而制造的。但是, 需要解决有关再现性、可预测性和尺寸公差水平的问题。

1.2 国内外研究现状

近些年来，许多学者在这些方面展开了大量的研究工作。目前在复合结构制造中使用的加工参数和固化周期通常源于经验，主要是迭代实验测试的结果。当前工艺开发方法的两个主要缺点是：需要进行广泛的实验测试以确定适当的固化周期，以及发现适合于一种应用的给定材料的固化周期通常用于不同材料或用于不同应用中的相同材料是不适用的。为了更好地研究树脂基复合材料在研制过程中固化、树脂流动、压实过程，使用数值模拟的方法是现今研究树脂基复合材料的常用手段。复合材料固化过程中固化变形的发展受到多个内在因素以及外在因素的影响，数值分析过程中，对这些因素的处理方式，将直接影响到计算的正确与否。大多数的研究者只针对关心的模块进行数值分析，而忽略整个固化过程相关的材料性质变化，以及多场耦合效应。对复合材料固化成型过程中的热-化学-应力耦合分析较为成熟，但大多数忽略了树脂的流动-压实问题，而对于固化过程中树脂的流动现象研究较少，与实际成型过程有一定距离。

1.2.1 流动-压实研究

在多孔介质中最早的固化和流动理论是Terzaghi^[1]提出的一维固化模型。继Terzaghi的一维理论之后, 又有了四个三维巩固理论被提出。第一个被称为Terzaghi 的三维理论, 是由 Terzaghi^[2]、 Rendulic^[3]和Barron^[4]提出的。第二个理论是由Biot^[5-7]提出的, 第三个是由Tan^[8]提出的。第四个是由Heinrich和Desoyer^[9]提出的。在这四种固化理论中, Terzaghi和Biot的理论是目前较为广泛运用的。

Cryer^[10]比较了Terzaghi和Biot 的三维固化理论对受静水压力作用下土壤饱和球体的研究结果。他的结论是, 对于在恒定加载条件下的一维固化 (这是在平面复合材料部件和结构制造过程中遇到的通常情况), 这两种理论是相同的。

固化理论认为多孔介质是固体颗粒的骨架, 封闭的空洞可能充满气体、液体, 或者两者兼而有之。多孔介质本身被认为表现得像弹簧。

在早期的一个模型中，Loos和Springer^[11]假设纤维压实是顺序的，从一个边界处的层开始。其他人认为纤维压实是分布性的，尽管在空间上变化，但在整个体积中发生。 然后Smith和Poursartip^[12]对这两个模型进行了比较，得出结论：顺序压实模型是后一种分布式压实模型的一个特例。其他工作包含了热性能和渗透性条件的本构模型。

Gutowski^[13]等人提出的“挤压海绵”模型，外界压力是由纤维和树脂的层压板共同承担，树脂承担的压力将推动树脂流经纤维床。因此, 树脂将沿垂直和平行模具表面的方向流出。由于纤维含量和孔隙比的变化, 纤维床的渗透率在过程中发生了变化。树脂的粘度是树脂温度和转化率的函数, 在工艺过程中也会随时间而变化。当树脂流出复合材料时, 树脂含量和层压板厚度降低。在层压板被压实后, 纤维床承担了更多的载荷。在固化结束时, 施加的外界压力全部由纤维床承担, 树脂压力降至零。

关于树脂流动模型与纤维压实模拟，目前主要存在两种理论,一种是 Loos 和 Springer^[11]提出的 “波浪式” 密实模式, 即 Sequential compaction 模型,在整个热压过程中树脂承担了全部外压而纤维层不承担压力且没有相互作用;另一种是Dave和Gutowski^[14-16] 等人提出的 “渐进式”密实模式,即 Squeeze sponge模型,外加压力由树脂和纤维共同承担。许多研究者根据 Squeeze sponge模型对热压工艺进行了数值模拟。

1.2.2固化过程研究

国内许多学者也对热固性树脂基复合材料进行了许多研究。Xie等^[21]考虑了高压釜中的框架模板和强制对流现象等因素，建立了高压釜中的固化度场、温度场仿真模型。在此基础上，对航空工业中的复合材料结构和材料体系进行了模拟和热分析。此外，对升温速率进行了研究，研究发现，增加保温时间和周期数可以显著改善温度场的均匀性，从而提高加热效率和温度场的均匀性；黄其忠^[19]等研究了复合材料先进网格结构固化工艺的温度场模拟，基于ANSYS软件开发了用于模拟复合材料固化过程中温度-固化度耦合场变化程序；Domínguez等^[20]利用DSC技术研究不同剂量的催化剂下，聚糠醇生物树脂的非等温固化动力学，为改进设计制造聚糠醇复合材料的固化周期，有一定的指导意义。Zhang等^[21]利用三维有限元模型的开发，模拟分析了环氧树脂构件固化过程中温度和固化度的发展。基于通用有限元软件ABAQUS，与实验数据对比验证，得到了准确的数值计算结果，成功地模拟了热对流换热系数和温度固化周期对固化温度和固化度的影响。陈淑仙等^[22]采用有限元方法，建立了热固性树脂基复合材料固化过程温度和热应力场分析的数学模型，进行了三维非稳态数值求解。通过与已有实验结果的比较，验证了数学模型和计算方法的正确性，并指出采用对称铺层可降低层合板内部温度梯度和热应力。Lander ^[23]等以数值模拟的方法阐述纤维层间特殊的纤维方向以及层合板整 体受压是如何导致褶皱产生的。Hubert^[24]等采用实验的方法研究两种采用热压罐成型工艺制作的碳纤维树 脂基复合材料在不同的树脂排出条件和模具条件下，层合板厚度、质量、局部纤维体 积分数的变化, Yoo^[25]等采用布拉格光栅传感器测量碳纤维树脂基复合材料应变，采用有 限单元法模拟分析环氧树脂的相变，并测定固化点对固化过程进行精确的模拟。

1.3 本文研究内容

本文通过建立厚L形复合材料层合板数学模型，计算结果与实验结果进行对比，验证了模型的正确性，建立了符合L形复合材料层合板模型的曲线坐标系，利用Comsol软件进行计算，分析了厚L形复合材料层合板固化过程中的流动-压实行为，研究了复合材料流动压实行为对纤维体积分数与有效应力的影响，预测了特定温度工艺与压力工艺条件下厚L形复合材料层合板的变形。

第2章 热固性复合材料流动压实固化模型及验证

2.1 热-化学模型

复合材料在固化的过程中温度分布以及固化度分布本质上是一个具有内热源的非线性热传导问题。瞬态热传导的控制方程,包括由于放热固化反应而产生的内部热，其热传导方程可以用傅里叶热传导定律和能量平衡原理建立数学模型，其表达式为：

(2.1)

其中：为复合材料的密度，为复合材料的比热，T为温度，t为时间；、、分别为复合材料在x、y、z方向上的热传导系数；为热生成率，可以表达为：

(2.2)

其中：为单位质量树脂固化总反应放热，为树脂密度，为纤维体积分数，为固化度，为固化速率，它与反应的热量一起决定了固化过程中的热释放率。

复合材料的密度和比热可基于混合法则计算：

(2.3)

(2.4)

其中，为纤维密度,为树脂体积分数。

对于3501-6树脂，其密度是关于固化度的函数，比热与热传导系数是关于温度T与固化度的函数，其表达式可以写作：

(2.5)

(2.6)

(2.7)

AS4碳纤维的密度不受温度影响，为常数，比热容和热传导系数为温度的线性函数，可以表达为：

(2.8)

(2.9)

(2.10)

由于复合材料的热传导系数具有各向异性，其垂直于纤维方向的热传导系数与平行于纤维方向的热传导系数不同，可以用Springer-Tsai模型进行计算，垂直于纤维方向上的热传导系数可以表达为：

(2.11)

(2.12)

平行于纤维方向的热传导系数可以表达为：

(2.13)

2.2 固化反应模型

AS4/3501-6复合材料固化反应动力学模型为

(2.14)

式中：

(2.15)

其中：是树脂体系的反应速率常数，是树脂体系的频率因子，是树脂固化反应活化能。在t=0时刻时：

=0 (2.16)

2.3 流动压实模型

当一个被不可压缩流体 (树脂) 充满的多孔纤维床在石墨/环氧复合材料的加工过程中受到压缩时, 树脂由于固化而通过纤维床的现象与当水在土壤内饱和而受到压缩应力实际情况相似。无论是纤维床还是饱和水土壤, 体积的减少几乎完全是由于液体含量的降低和固体成分的体积减少, 孔隙中的液体可以忽略不计。

层压复合材料的固化类似于通过多孔介质的流动现象。因此, 达西定律可以用来描述固化过程中层压板中的树脂流动。对于含有不可压缩流体的多孔介质在孔隙内的固化, 通过平衡方程给出应力, 如下所示:

(2.17)

其中，是外界压力，是树脂承担的压力，纤维网格上的有效纤维应力。

Dave等人^[16]采用有限差分法研究了层压板厚度的影响以及轴向与横向流动的影响,在他的模型中,流动阻力被认为可以忽略不计, 层压板界面的压力等于真空袋中的压力。从他的模拟中得出的主要结论是, 考虑到层压厚度, 在达到凝胶点之前，树脂压力下降到真空袋压力。对于较厚的层压板, 压力衰减较慢。层压板在轴向和横向上都存在树脂压力梯度。对于厚层压板, 大部分流动是轴向的。对于薄层压板来说, 大部分的流动都是横向的。

他给出了微分控制方程，通过求解流动方程来评估树脂压力分布：

(2.18)

其中，为纤维沿x,y,z方向的渗透率，是体积变化系数，可以表达为：

(2.19)

其中，e为单位体积的孔隙率，其表达式为：

(2.20)

Shin和Hahn^[26]给出了纤维体积分数与有效纤维应力之间的关系：

(2.21)

其中，, a, b 是经验常数。这些常数是通过假设复合材料遵循与 Dave 工作中描述的堆叠纤维相似的压缩行为来确定的。

纤维床的渗透性描述了多孔介质对流体流动的阻力。在层压板固化过程中，树脂流动会导致纤维体积分数的变化。因此, 纤维床的渗透率是纤维体积分数的函数。

Carman-Kozeny 方程通常用于描述可变孔隙度介质的渗透率，沿平行于纤维方向(x方向)的纤维床渗透率的表达式为：

(2.22)

沿垂直于纤维方向(y、z方向)的纤维床渗透率的表达式为：

(2.23)

其中，、为Carman-Kozeny常数，为纤维半径。

2.4 树脂粘度模型

树脂的粘度影响着树脂流速，是树脂温度和固化度的函数, 在工艺过程中也会随时间而变化。在树脂液体阶段, 树脂粘度受到两个主要现象的影响：首先是分子的生长大小, 这增加了树脂粘度。二是温度对分子流动性的影响。因此, 树脂粘度μ取决于T和α。 在文献中发现了不同的树脂粘度模型方法。Dusi等人^[27](1987年)和Lee等人^[28] (1982年)提出了以下经验关系:

(2.24)

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：