摘 要

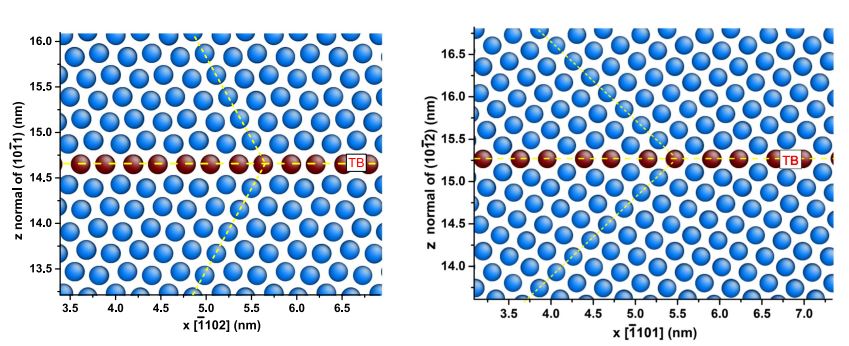
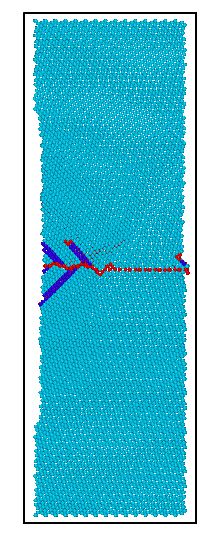
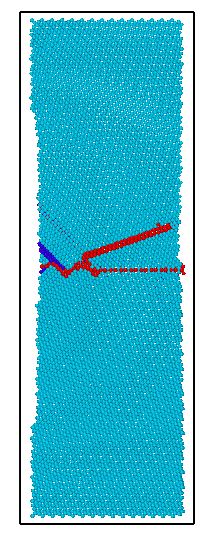
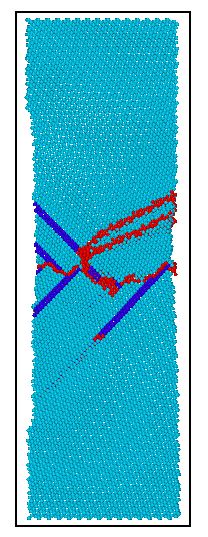
镁及其合金近年来受到了广泛的关注，这不仅仅因为镁具有很多的优点，更与镁中存在的多种缺陷及其变化机理有关。镁作为一种典型的密排六方结构的金属，孪生和位错是其最主要的变形机制，而孪晶界是一种很常见的缺陷，因此研究孪晶界对镁晶体变形行为及力学性能的影响就显得很重要。本文采用分子动力学模拟软件LAMMPS对含不同孪晶界类型和不同孪晶界间距的镁晶体模型进行单向拉伸模拟，探究不同模型在拉伸过程中的微观变形机理，重点讨论了孪晶界间距对镁拉伸屈服强度及变形行为的影响。模拟结果表明：含有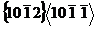孪晶界的模型，基面层错的形成及扩展是导致塑性变形的主要机制，含有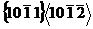孪晶界的模型，塑性变形行为与锥形位错的萌生及扩展及孪晶界的迁移和分叉有关；两种孪晶界的引入均导致镁拉伸屈服强度降低，孪晶界间距越小，屈服强度越低。本文将对镁及镁合金力学性能的研究提供一定的理论参考。

关键词：分子动力学模拟；孪晶界间距；位错；力学性能

Abstract

Magnesium and its alloys have attracted extensive attention in recent years, not only because of its many advantages, but also because of various defects and their changing mechanism. As a typical hexagonal metal, twinning and dislocation are the main deformation mechanism. As a common defect, it is very important to study the effect of twin boundary on the deformation behavior and mechanical properties of magnesium. In this paper, the unidirectional tensile simulation of magnesium model with different twin boundary types and spacing was carried out by molecular dynamics simulation software LAMMPS. The micro-deformation mechanism of different twin boundary during tensile process was investigated, and the effect of the spacing of twin boundary on the tensile yield strength and deformation behavior of magnesium was discussed. The simulation results show that the main mechanism of plastic deformation is the formation and expansion of the basal plane stacking faults in the model with 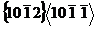twin boundaries. The model with 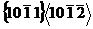twin boundaries is related to the initiation and expansion of conical dislocations and the migration and bifurcation of twin boundaries. The introduction of both twin boundaries results in the reduction of tensile yield strength of magnesium, and the smaller the spacing between twin boundaries, the lower the yield strength. This paper will provide some theoretical reference for the study of mechanical properties of magnesium and magnesium alloys.

Key words: molecular dynamics simulation; twin boundary spacing; dislocation; mechanical properties

目录

摘 要 I

Abstract II

第1章 绪论 1

1.1 研究背景 1

1.2 国内外研究现状 1

1.3 研究内容 2

1.4 预期目标 2

第2章 分子动力学模拟理论 3

2.1分子动力学基本思想与方法原理 3

2.2分子动力学方法的基本方程 4

2.2.1牛顿方程 4

2.2.2哈密顿运动方程 5

2.3系综简介 6

2.3.1微正则系综（NVE系综） 7

2.3.2正则系综（NVT系综） 7

2.3.3等温等压系综（NPT系综） 7

2.3.4巨正则系综（VT系综） 7

2.4边界条件 7

2.4.1周期性边界条件 8

2.4.2自由边界条件 8

第3章 孪晶界对镁晶体变形行为的影响 10

3.1建模和模拟方法 10

3.1.1建模 10

3.1.2模拟方法 11

3.2含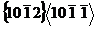孪晶界镁晶体的拉伸模拟 11

3.2.1含一条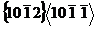孪晶界镁晶体的拉伸模拟分析 11

3.2.2含二条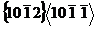孪晶界镁晶体的拉伸模拟分析 13

3.2.3含三条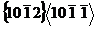孪晶界镁晶体的拉伸模拟分析 16

3.3 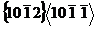孪晶界间距不同镁晶体模型的拉伸模拟比较 18

3.4含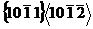孪晶界镁晶体的拉伸模拟 20

3.4.1含一条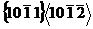孪晶界镁晶体的拉伸模拟分析 20

3.4.2含二条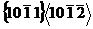孪晶界镁晶体的拉伸模拟分析 22

3.4.3含三条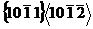孪晶界镁晶体的拉伸模拟分析 24

3.5 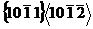孪晶界间距不同镁晶体模型的拉伸模拟比较 27

3.6 本章小结 28

第4章 结论与展望 29

4.1 主要结论 29

4.2 工作展望 29

参考文献 30

致谢 32

绪论

研究背景

纯镁的密度很小，只有 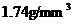，是工业用金属中最轻的一种，由于其弹性模量小，在外力作用下能够产生较大的变形以吸收能量，故可用于制造承受冲击载荷的零件。镁合金的比强度、比刚度、抗冲击性较铝合金高，抗震能力强，多用于导弹、卫星和装甲车部件等，被誉为“21 世纪绿色工程材料”。我国是世界上镁资源最丰富的国家，原镁年产量超过50万吨，产能、产量和出口均位居世界前列。随着新世纪的到来，工业进一步发展，绿色能源更加被重视镁作为一种绿色工程材料，其开发应用空间将进一步扩大，而镁资源也将发挥更加重要的作用。然而镁及其合金的应用因其较低的强度和延伸性受到极大的限制，而这都与它的初始形变机理相关，因此对镁及其合金变形的研究备受欢迎。

孪生对镁的塑性变形有很多方面的作用，也是镁合金的主要塑性变形方式之一。孪晶界在金属中很常见，能够使材料表现出较好的力学性能。研究发现，可以通过引入孪晶界来获得高强度合金，一个显著的例子就是通过在细晶铜中引入高密度的生长孪晶,使材料拥有较高的强度,同时还能保证良好的断裂伸长率。因此探究孪晶界对镁的变形行为和力学性能的影响显得尤为重要。

国内外研究现状

目前对于镁的应用主要受限于其强度和延展性，相关的研究也主要集中于此。Xin等人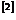的研究表明，高速变形促进了孪生的产生，初始取向对孪生的形核具有重要影响。由于镁合金很强的各向异性力学性能及应变硬化行为，少量{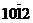}拉伸孪生的发生可以引起明显的屈服现象；Wang等人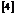研究了AZ31 镁合金在以孪生主导的塑性变形中的力学行为。结果表明，当压缩孪晶是一种重要的变形机制时，总应变要大于0.15。因此，尽管压缩孪晶内部存在应变局域性，但在断裂前仍能适应相当大的变形。{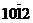}孪晶发生在塑性变形开始时，这些孪晶消耗并重新定向有利的晶粒；Zu等人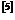研究了不同晶格取向的镁单晶初始塑性变形行为。结果表明，载荷与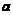方向或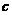方向的夹角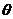影响镁的初始塑性变形和演化，当夹角趋向于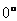时，在拉伸和压缩荷载下都出现了孪晶；Song等人研究了镁的孪生行为,结果表明纳米级孪晶镁孪生区的厚度对镁的屈服强度和杨氏模量有极大影响；单智伟等人的研究表明，如果迁移中的{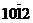}孪晶界遇到障碍物, 那么孪晶界可以通过另外一种方式绕过。上面这些研究均表明孪晶界与镁的力学性能有极大联系。因此，为提高镁的力学性能，对孪晶界的深入研究是十分有必要的。本文的焦点基于此，研究含有不同类型、不同间距孪晶界对的镁在单向载荷作用下的变形过程及相关力学性能。

研究内容

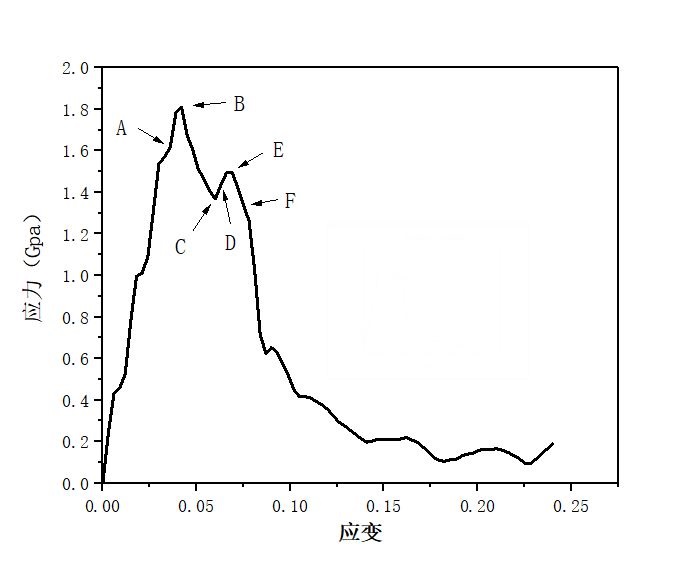
本文利用分子动力学模拟软件LAMMPS研究不同孪晶界间距对镁的基本力学性能和变形行为的影响。主要研究内容包括：用LAMMPS 结合合适的作用势，模拟含有不同孪晶界间距的镁在单向拉伸作用下的微观变形机理，分析应力-应变曲线的变化过程，讨论镁内部缺陷的形成、演化过程。充分考虑孪晶界间距对屈服应力、流动应力及微观变形机理的影响。

预期目标

本论文通过计算不同孪晶界间距对镁的变形行为的影响，结合拉伸载荷下的应力—应变曲线分析材料微观结构的转变，观察镁模型内部缺陷成核、演化过程，讨论了孪晶界间距与镁拉伸强度之间的关系。从微观尺度对镁的拉伸破坏行为做进一步的解释。

分子动力学模拟理论

2.1分子动力学基本思想与方法原理

分子动力学方法的基础是分子力场，它通过计算机模拟的方法求解运动方程并分析体系的结构和性质。早在1957年，分子动力学模拟就己经实现。在分子动力学模拟发展早期，研究重点主要基于分子动力学模拟算法与应用．但对其理论基础研究的较少，重视程度不够。早期的数值积分算法强调计算效率和精度而忽略了运用差分方法的过程中误差的积累，这就使得差分算法有可能失稳甚至严重影响模拟结果的可靠性。

由于分子动力学方法是通过原子体系内部的运动学规律以确定体系原子的位置，因此需要建立原子的运动方程并进行求解从而得到原子在某个时刻的坐标。动力学的基本思想在于设定原子间的相互作用和作用的对象和条件也即势函数和系综。分子动力学基本原理是建立包含多个原子钢球粒子模型的物理系统，由于每个粒子满足经典牛顿力学定律或者拉格朗日方程，可以对粒子建立牛顿动力学方程，求解方程从而得到所有粒子在各个时刻的坐标，最后根据统计物理方法描述原子的运动特性以及系统的整体或局部特性。如图 2-1 所示为分子动力学计算流程图。

分子动力学的模拟程序包含以下几个步骤：

（1）

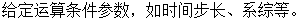
（2）

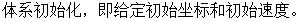
（3）

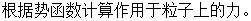
（4） 根据体系粒子的基本信息求解牛顿方程，直到计算体系满足所给判定条件。

（5） 分析所得物理量，计算测量值平均值，结束模拟。

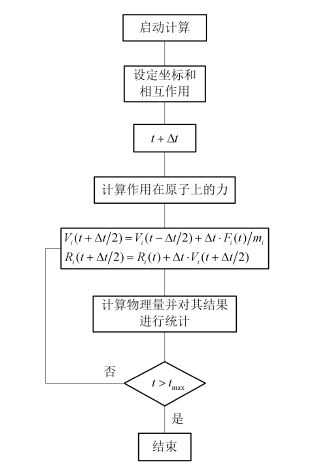
图2-1 分子动力学计算流程图

2.2分子动力学方法的基本方程

2.2.1牛顿方程

在微观尺度上，原子核占据了原子的大量质量，那么在计算模拟过程中就可以把原子看作是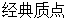，而分子体系就可以被看作是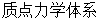。由可得分子体系的运动方程为

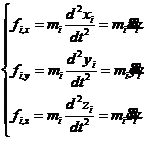（2-1）

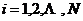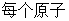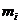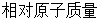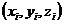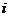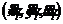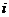式中，，用来标注分子体系中的；表示每个原子的；t表示时间；表示原子的位置坐标； 表示原子的位置坐标相对于时间的二阶导数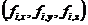；表示作用于原子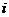上的力在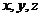坐标轴方向上的分量。可以通过计算分子内相互作用力和分子间相互作用力进而求得作用于原子上的力。另外也可将式（2-1）用矢量式表示为

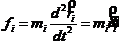（2-2）

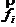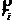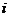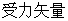上式中，和分别表示原子的与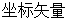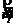；表示坐标矢量相对于时间的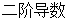。与式（2-1）完全相同，式（2-2）同样也代表3N个方程。

2.2.2哈密顿运动方程

由前述可知，分子动力学可以看做是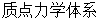，这个体系由存在着相互作用的原子组成。对于分子体系来说，不管是哪种相互作用，这个体系中原子之间的相互作用总是保守力。而原子可以看做是质点，由质点构成的保守力体系的哈密顿函数可以写成如下形式

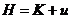（2-3）

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：