基于近场动力学方法的动态裂纹扩展毕业论文
2020-02-18 10:04:38
摘 要
在大部分的工程材料和结构中,由于结构不合理或材料本身存在缺陷和微裂纹,材料在服役过程中会产生较高的局部应力,进而导致缺陷与微裂纹的扩展和增殖。这些裂纹可能会导致材料的破坏和失效,并威胁到整个结构的安全。因此,研究裂纹扩展与材料失效在工程材料应用与结构设计领域具有重要意义。由于基于经典连续介质力学理论的网格类数值方法在处理裂纹扩展这类不连续问题时存在困难,本文采用基于键的近场动力学理论构建脆性材料的线弹性材料模型,并对含预置裂纹的二维板在外载荷作用下的I型裂纹扩展问题进行了数值模拟研究。本文的主要工作如下:
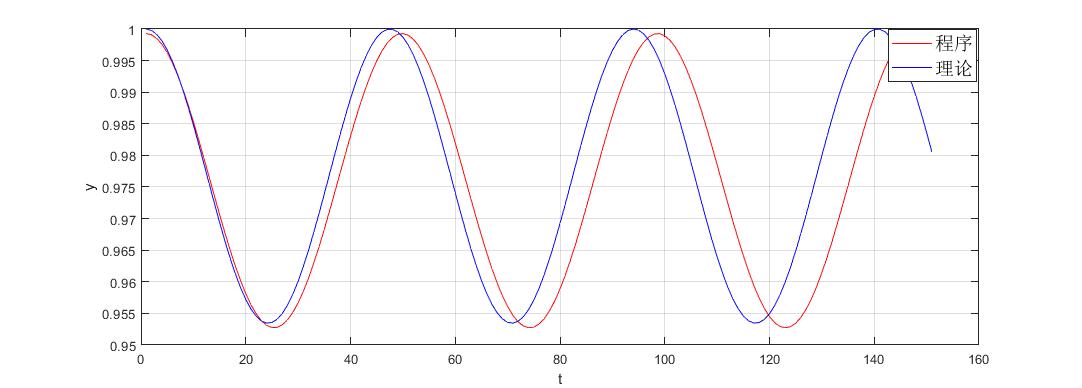
1、采用基于键的近场动力学理论,根据脆性材料线弹性材料模型(PMB模型),编写二维线弹性材料近场动力学计算程序,并使用该程序计算了悬臂梁在自由端集中外载荷作用下的力学响应。通过将近场动力学计算结果与理论解和ABAQUS有限元解对比,证明了所编写近场动力学程序的正确性。
2、基于已验证的程序对预制裂纹的二维杜兰玻璃板I型裂纹扩展过程进行了数值模拟研究。通过更改外载荷大小,研究裂纹扩展过程与应变率之间的关系。结果表明,当载荷较小时,裂纹呈直线型扩展,并且不发生裂纹分叉。随着外荷载与应变率的增大,裂纹的分叉次数与总的裂纹数量也随之增大。通过对相同时刻裂纹扩展过程中的应变能密度进行可视化对比,可以发现,裂纹尖端附近伴随着弹性应变能集中现象。
本文克服了传统连续介质力学求解裂纹扩展的困难,且研究成果可为后续利用基于态的近场动力学理论进一步研究裂纹扩展提供基础。
关键字:基于键的近场动力学,弹脆性模型,悬臂梁振动,裂纹扩展
Abstract
In most engineering materials and structures, due to structural irrationality, defects and microcracks in the material itself, there will produce stress concentration during service, which may lead to the expansion and proliferation of defects and microcracks. Those cracks can cause damage and failure of the material and thus threaten the safety of the entire structure. Therefore, it is of great significance to study crack propagation and material failure in the field of engineering materials application and structural design. Because the grid-based classic numerical methods those based on classical continuum mechanics theory have difficulties in dealing with discontinuities such as crack propagation, in this paper we use the bond-based Peridynamics theory to construct a linear elastic material model of brittle materials. The numerical simulation of the crack propagation of the two-dimensional plate with crack under the external load is carried out. The main work of this paper is listed as follows:
Under the framework of the bond-based Peridynamics theory, the calculation program of two-dimensional linear elastic material is written, incorporating the Prototype Micro Brittle(PMB) model of brittle material linear elastic material model. The program is used to calculate the cantilever beam mechanical response under the free end external load. By comparing the Peridynamics calculation results with the theoretical solution and the ABAQUS finite element solution, the correctness of the written Peridynamics program is proved and verified.
Based on the verified program, the numerical simulation of the crack propagation process on the two-dimensional Duran glass plate with pre-notch was carried out. The relationship between the crack propagation process and the strain rate was studied by changing the external load. The results show that when the external load is small, the crack expands linearly and there is no crack branching. As the external load and strain rate increase, the bifurcation probability of cracks and the distribution density of cracks also increase. By comparing the strain energy density visually during crack propagation at the same time, it can be found that the elastic strain energy concentration phenomenon is accompanied by the crack tip.
This paper overcome the difficulties that traditional mechanical methods have to solve crack propagation, and the research results can provide a basis for further research on crack propagation by using state-based theory.
Key Words:Bond-based Peridynamics, PMB Model, cantilever beam vibration, crack propagation
目录
第1章 绪论 1
1.1研究的背景、目的和意义 1
1.2国内外研究现状 1
1.3本文的主要研究内容 2
第2章 近场动力学理论与后处理工具 3
2.1 近场动力学理论 3
2.1.1 基于键的近场动力学理论 3
2.1.2 弹脆性模型(PMB) 5
2.2 后处理工具 6
2.2.1 MATLAB数据处理 6
2.2.2 Tecplot可视化软件 6
第3章 近场动力学程序实现与验证 7
3.1 近场动力学程序实现 7
3.1.1空间离散及时间离散 7
3.1.2变量 7
3.1.3数据存取 9
3.1.4功能函数 10
3.1.5 断键判断 10
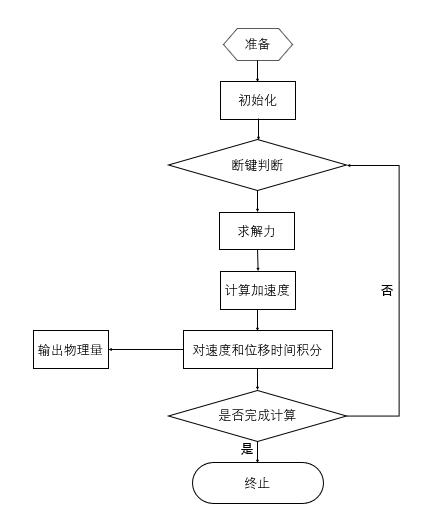
3.1.6 程序流程 11
3.2 近场动力学程序验证 12
3.2.1 悬臂梁的数值模型 12
3.2.2 悬臂梁的理论解 14
3.2.3 数据对比与验证 15
3.3 对比与小结 20
第4章 预置裂纹二维板的I型裂纹扩展研究 21
4.1 数值模型 21
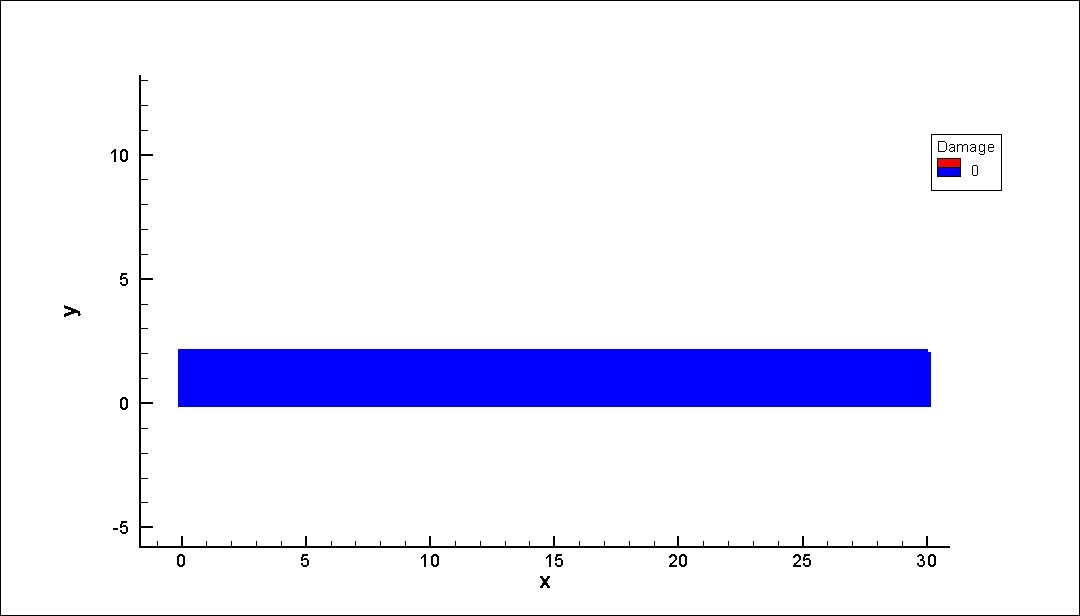
4.1.1 二维平板模型 21
4.1.2 模拟参数 22
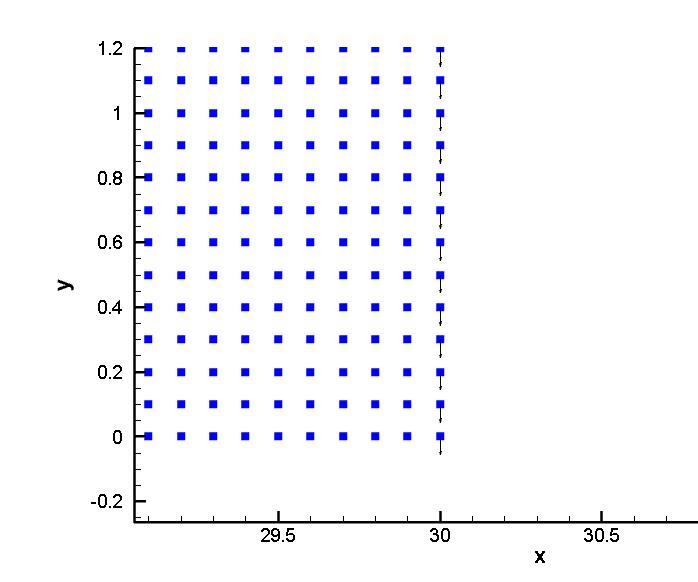
4.1.3 预置初始裂纹 22
4.2 二维板I型裂纹动态扩展过程 23
4.3 外载荷变化对裂纹扩展路径的影响 27
4.4 小结 31
第5章 总结与展望 32
5.1 总结 32
5.2 展望 32
参考文献 33
致 谢 34
第1章 绪论
1.1研究的背景、目的和意义
在大部分的工程材料和结构中,都不可避免的存在缺陷。如金属材料本身存在疏松、非金属夹杂物等缺陷,在制造钢材过程中会产生初始轧制裂纹;在金属容器的制造过程中,由于工艺不良等原因会产生大量的细微焊接裂纹;由于结构不合理或材料本身存在缺陷,在使用过程中会导致这些缺陷附近产生较高的局部应力,进而导致裂纹形成与扩展。这些缺陷的存在并不一定会立刻危及结构的安全性或可靠性,但在材料和结构的长期服役过程中,这些缺陷和裂纹可能会在特定外部条件下产生严重的后果,甚至威胁到整个结构的安全。
历史上,因为材料内部的裂纹形成和裂纹扩展导致材料失效,并因此引发过许多重大工程事故。1998年6月3日上午11时左右,德国城际快车ICE884次列车—“威廉·康拉德·伦琴”号发生严重脱轨事故,12节车厢以接近200km/h的速度撞击到雷贝拉大街的一座混凝土公路桥的桥墩上,导致整座桥倒塌,造成101人死亡。事故发生后经过调查发现造成事故的最重要原因是:列车车轮原本是单铸铁一体成型,因为车身震荡与噪声问题,后改为车轮外由一层20mm厚的橡胶包裹,再外套一个相对薄的金属车轮,而由于工作人员的疏忽没能检查出该车轮内侧存在一道微细裂纹,在列车高速运行的过程中,裂纹不断扩展,最终导致出故障的车轮完全断裂,造成无法挽回的后果。
因此,除了在实际服役过程中对材料早期裂纹进行必要防范之外,研究并预测裂纹在外载荷作用下的动态扩展和因此而导致的材料失效对工程材料的应用就显得尤为重要,明确复杂条件下的裂纹生成与扩展规律对工程结构设计和材料的应用具有非常重要的指导性意义。
1.2国内外研究现状
经典的连续介质力学模型是以位移分量的偏微分方程为基础、基于连续性假设建立的,这样会导致在不连续处(裂纹、缺陷等),位移的偏导数不存在,产生奇异性。此时应用经典连续介质力学预测裂纹尖端的应力则会变为无穷大,必须引入附加的外部准则来消除这一错误。而传统的有限元法、有限单元法、有限差分法的理论基础就是连续介质力学,它们在裂纹扩展后必须重新划分网格,因此通常无法模拟材料的离散破坏和裂纹的扩展。为解决以上困难,基于传统有限单元法(FEM),Wagner G J等人提出了扩展有限元法(XFEM)[1],但是应用到复杂裂纹问题时,效果依然不理想,利用连续理论求解非连续问题存在不可避免的矛盾。
研究人员也尝试了各种无网格解法,如光滑粒子动力学(SPH)[2]和无网格伽辽金法(EFGM)[3]等,但是始终克服不了连续性与不连续问题这一关键矛盾,并且要对材料破坏过程中数量庞大的裂纹进行追踪研究,也是极其困难的。而无网格法中的经典分子动力学(MD)[4]方法,在模拟宏观材料行为时会受到求解尺度的限制,导致计算消耗时间长、计算效率低下等一系列问题。
常用的数值方法都含有或大或小的缺陷,有些还有特定的使用范围,研究人员迫切需要能够综合各种方法的优点的通用理论。
为了解决这一根本矛盾,美国 Sandia 国家实验室的Silling教授在2000年提出了近场动力学(Peridynamics,PD)理论[5]。近场动力学理论是将固体离散为空间域内一系列包含物理信息的质量点,利用节点力的积分代替运动方程中的空间导数。PD理论的本构模型相对简单,本构模型一旦确定,当断裂能达到一定值时,域内任意位置的裂纹的萌生和扩展可以自发产生,不需要引入任何额外的裂纹扩展准则,此外PD理论提出了“近场尺寸”(Horizon)的概念,在PD理论中,处于近场尺寸范围内的质量点之间会产生相互作用力。因为PD理论中采用积分方程代替了偏微分方程,因此PD 理论不需要位移场连续可微,在多尺度模拟和裂纹问题上具有突出的优越性。近年来许多专家学者在PD领域上取得了大量的研究成果,逐步完成了PD方法的理论体系的构建[6][7],并成功应用于多尺度材料和结构的力学分析中,也逐渐开发了Peridigm等近场动力学计算软件,使PD方法应用在越来越多的工程领域。
1.3本文的主要研究内容
由于PD方法在研究裂纹扩展问题上的优势,因此本文在近场动力学理论框架下,构建理想弹脆性(PMB)材料模型,并对裂纹动态扩展进行数值模拟。主要研究工作包括:
- 用基于键的近场动力学(PD)理论实现理想弹脆性方程,运用C语言编写PD计算程序,并调试成功。
- 用编写的PD计算程序试算悬臂梁自由振动力学算例,并与悬臂梁自由振动解析解及ABAQUS仿真的结果对比,验证程序的正确性。
- 建立二维平板预制裂纹的数值模型,模拟均布受拉载荷作用下的断裂过程,并将断裂过程可视化。
- 分析其裂纹动态扩展过程,并探讨作用力大小等因素对平板裂纹扩展的影响。
第2章 近场动力学理论与后处理工具
2.1 近场动力学理论
近场动力学理论—Peridynamics(下文简称PD),来源于希腊词根“near”和“force”。PD基础理论是2000年由美国 Sandia 国家实验室的Silling教授提出[5],早期叫做“Bond-based”(基于键)理论,这个理论可以较好地解决一些不连续问题,但是基于键的PD理论对材料的泊松比有限制,无法反映很多材料的泊松效应,且不能表示剪切,因此Silling于2007年将理论完善[6],提出了“State-based”(基于态)理论,并将“Bond-based”(基于键)理论作为一种特殊情况包含其中。基于态的理论引入了应变梯度和应变张量,可以直观描述弹塑性材料的本构关系,并完整的将连续介质力学的概念继承了下来,使得近场动力学理论应用范围越来越广阔。
本文的内容将围绕基于键的PD理论展开。
2.1.1 基于键的近场动力学理论
基于键的近场动力学理论可以看做是宏观下的连续的分子动力学,其核心在于基于非局域思想建模,将运动方程由一个积分形式表达。如图2.1所示,如果一个物体占据了空间域R,则在任意时刻t,空间域R内任意一物质点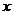 与其周围一定范围
与其周围一定范围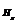 内的每一物质点
内的每一物质点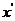 存在相互力的作用,满足方程:
存在相互力的作用,满足方程:
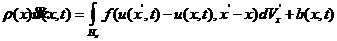 (2.1)
(2.1)
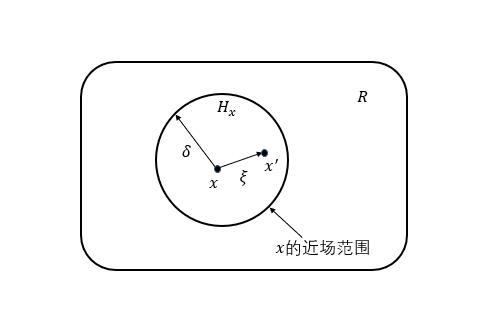
图2.1 近场动力学示意图
其中,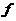 表示材料点
表示材料点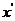 对材料点
对材料点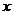 的作用的应力矢量函数,单位是每单位平方体积;
的作用的应力矢量函数,单位是每单位平方体积;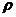 为材料点的质量密度;
为材料点的质量密度;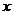 为物质点的位置;
为物质点的位置;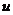 为物质点的位移;
为物质点的位移;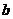 是单位体积物质所受外荷载,即外力密度;
是单位体积物质所受外荷载,即外力密度;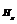 是以物质点
是以物质点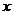 为圆心,
为圆心,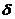 为半径的球域,称作近邻范围,即:
为半径的球域,称作近邻范围,即:
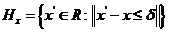 (2.2)
(2.2)
由公式(2.1)可知,PD理论中,物质点之间的本构力函数包含了材料的所有属性,而不是以传统的应力应变关系出现,运动方程中也不存在空间导数,从而无论位移场是否连续,均不会影响方程的求解。
如果将参考系中两个粒子的相对位置记作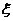 ,相对位移记作
,相对位移记作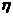 ,则有:
,则有:
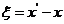 ,
,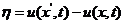 (2.3)
(2.3)
基于以上定义,则当前时刻两粒子的相对位置为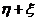 ,矢量
,矢量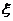 命名为“键”(bond),
命名为“键”(bond),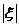 为变形前作用键的长度,
为变形前作用键的长度,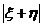 为变形后作用键的长度,如图2.2所示。作用在有限距离的“键”的概念是基于彼此直接接触的粒子之间的接触力产生的,这是近场动力学理论与经典连续介质理论的根本区别。
为变形后作用键的长度,如图2.2所示。作用在有限距离的“键”的概念是基于彼此直接接触的粒子之间的接触力产生的,这是近场动力学理论与经典连续介质理论的根本区别。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: