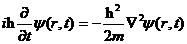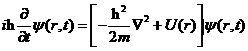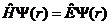硼化钛的剪切变形机制的第一性原理计算毕业论文
2020-02-18 10:04:46
摘 要
本文采用基于密度泛函理论的第一性原理计算方法,利用软件Vienna ab-initio Simulation Package(VASP)计算了二硼化钛的基本材料性质,研究了二硼化钛在不同方向的剪切外荷载下的力学行为,分析了其相应的微观变形机制。计算结果表明,二硼化钛在不同方向上的弹性性质有差异,反映出较强的各向异性,同时它的抵抗剪切变形的能力较弱,延展性较低。二硼化钛的电子结构表明,它的电子能量呈局域化不均匀分布,B-2p轨道和B-2s轨道存在杂化现象,提高了键能及体系抵抗变形的能力。B-B键和Ti-B键是结构承受外荷载及抵抗变形的关键,它在剪切荷载下的断裂情况影响结构的稳定性,不同滑移系下,当应变达到临界应变时,化学键断裂,此后结构的应力迅速减小,结构破坏。研究二硼化钛在剪切载荷下的变形行为,对于理解它的力学特性以及扩展其应用具有重要的理论指导意义。
关键词:二硼化钛;第一性原理;力学性质;电学性质;剪切变形机制
Abstract
In this paper, the first principle method based on density functional theory is adopted to calculate the basic material properties of titanium diboride by using Vienna ab-initio Simulation Package (VASP). The mechanical behavior of titanium diboride under shear load in different directions is studied, and the corresponding microscopic deformation mechanism is analyzed. The results show that the elastic properties of titanium diboride in different directions are different, which reflects the strong anisotropy, and its resistance to shear deformation is weak, and its ductility is low. The electron structure of titanium diboride shows that its electron energy is localized and unevenly distributed, and hybrid phenomena exist in B-2p orbital and B-2s orbital, which improves the bond energy and the system's resistance to deformation. B-B bond and Ti-B bond are the key factors for the structure to bear external load and resist deformation. The fracture of them under shear load affect the stability of the structure. Under different slip systems, when the strain reaches critical strain, the chemical bond breaks, and then the stress of the structure decreases rapidly and the structure is destroyed. The study of the deformation behavior of titanium diboride under shear load has important theoretical significance for understanding its mechanical properties and extending its application.
Keywords: titanium diboride; first principles; mechanical properties; electrical properties; shear deformation mechanism
目录
摘要 I
Abstract II
第1章 绪论 1
1.1研究背景 1
1.2 国内外研究现状 2
1.3 研究内容 2
1.4 预期目标 3
第2章 第一性原理 4
2.1 第一性原理简介 4
2.2 波函数及薛定谔方程 4
2.3 近似简化方法 5
2.3.1 Born-Oppenheimer近似 5
2.3.2 Hartree-Fock近似 6
2.4. Thomas-Fermi模型 7
2.5 密度泛函理论 7
2.5.1 Hohenberg-Kohn定理 7
2.5.2 Kohn-Sham 方程 8
2.5.3 局域密度近似(LDA)方法 8
2.5.4 广义梯度近似(GGA)方法 9
2.6 本章小结 9
第3章 硼化钛晶体结构及优化 10
3.1 晶体模型 10
3.2 结构优化 10
3.3 优化结果 11
3.4 本章小结 11
第4章 硼化钛的力学性质和电学性质 12
4.1 计算模型 12
4.2 力学性质 12
4.2.1 弹性常数 12
4.2.2 弹性模量 13
4.3 电学性质 14
4.4 本章小结 15
第5章 硼化钛的剪切变形机制 16
5.1 剪切变形行为 16
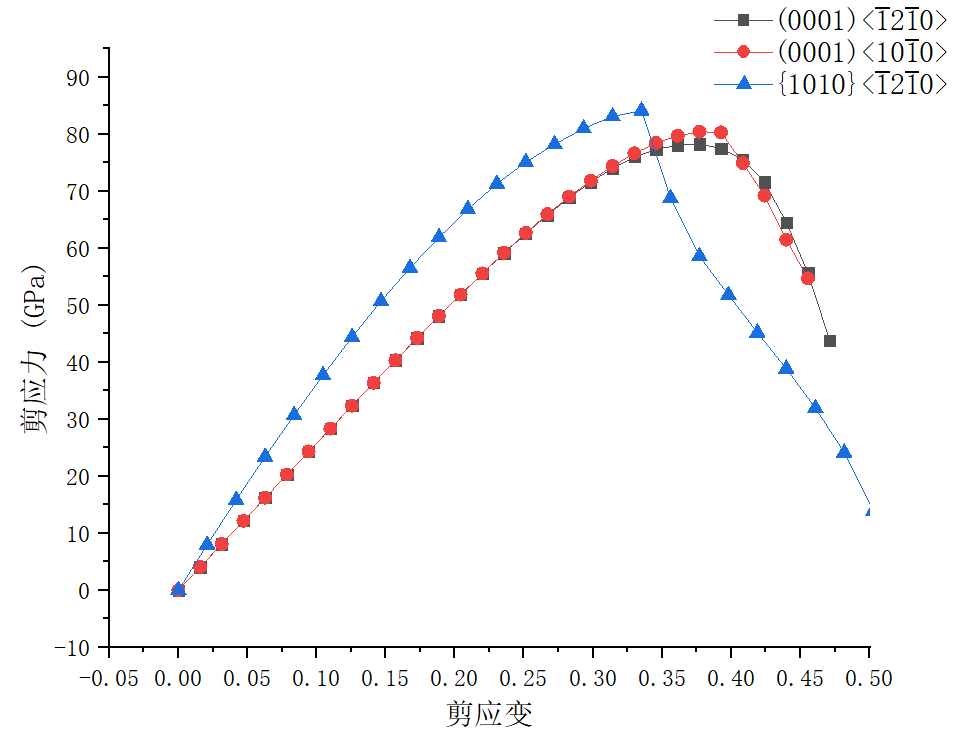
5.1.1 应力与应变关系 16
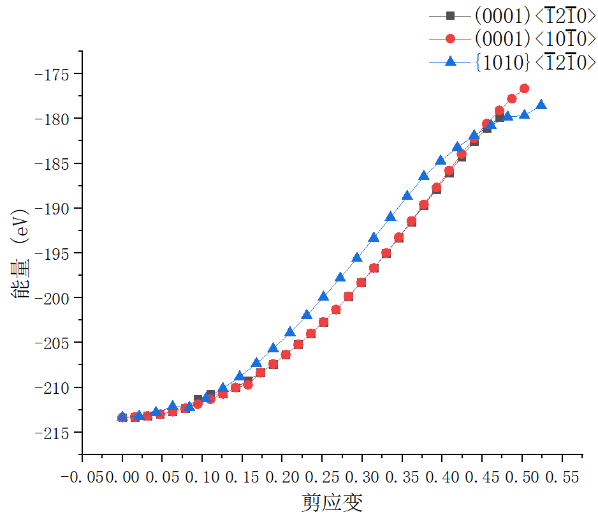
5.1.2 能量与应变关系 17
5.2 微观变形机制 18
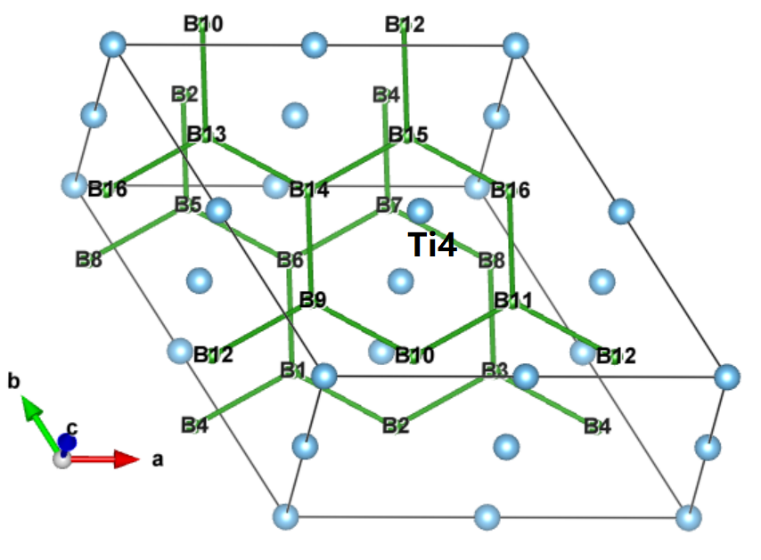
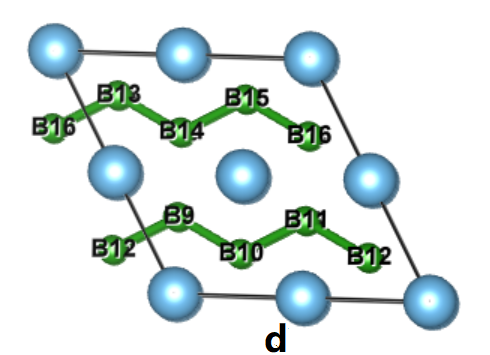
5.2.1 原子间距和键长分析 18
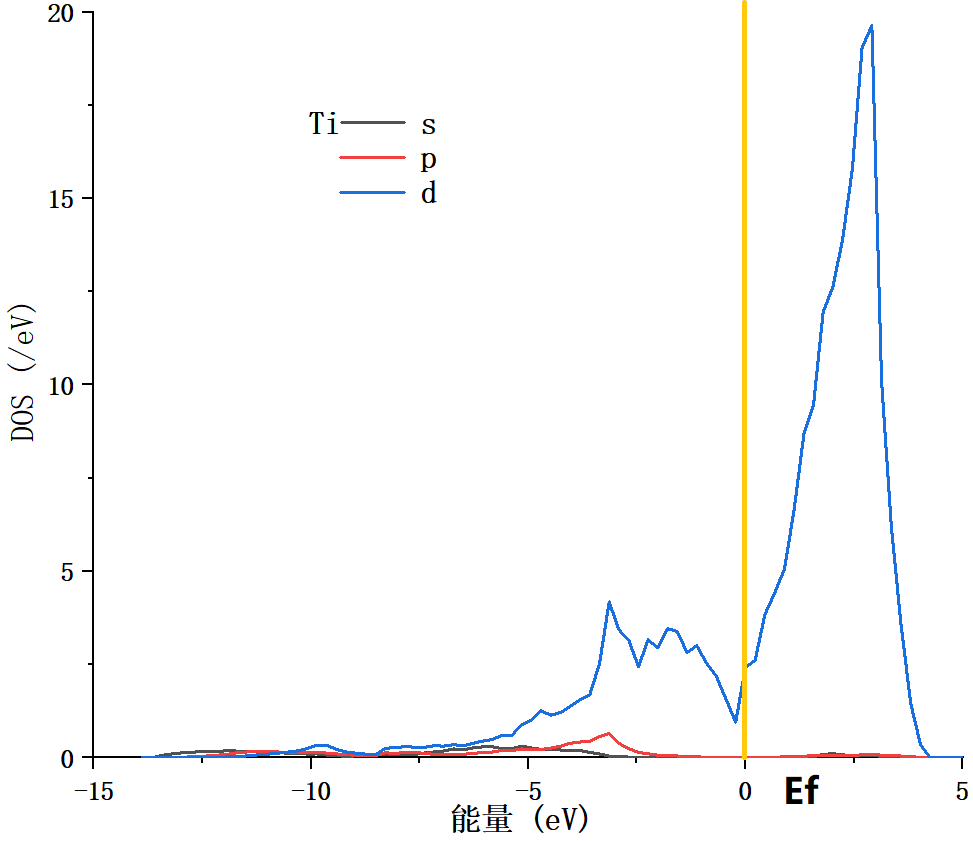
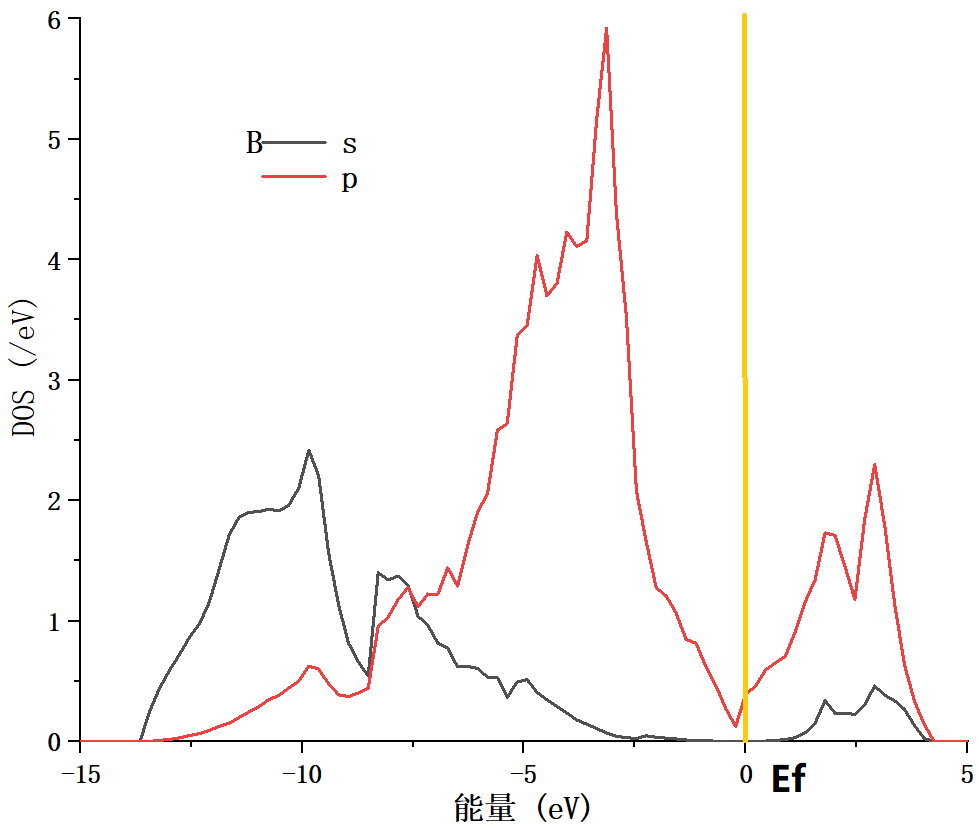
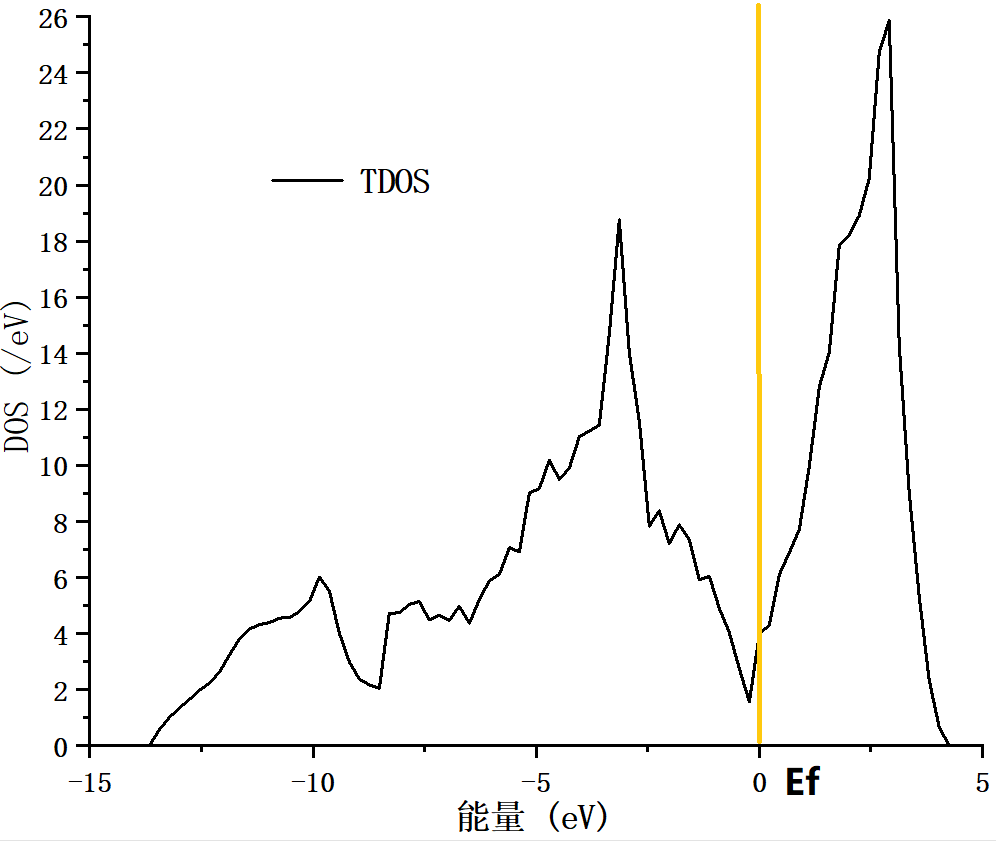
5.2.2 电子态密度变化 21
5.3 本章小结 23
第6章 总结与展望 24
6.1 主要结论 24
6.2 工作展望 24
参考文献 25
致谢 27
第1章 绪论
1.1研究背景
硼化钛近年来以其硬度大、熔点高、耐磨性良好、导电性高、耐腐蚀性好、热力学稳定性高以及电阻率低等优良特性得到了广泛的关注,主要应用于抗冲击装甲、切割工具、耐磨零件、晶粒细化剂、填充剂、各种高温结构材料、电解槽电极[1]、涂层镀层[2]、超大规模集成电路[3]等领域。此外,由于研究手段的日益精进和实际应用需求的多元化,纳米尺度的硼化钛晶体也成为人们的关注热点。根据Efimova K A[4]等人的实验结果,二硼化钛纳米颗粒可以在碳-氢等离子体流中由钛-硼和二氧化钛-硼粉末混合物制得,产物二硼化钛纳米粉体可应用于碳阴极可润湿性涂料之中。一种改良的高温自蔓延反应稀释法也被人提出,这种方法可以克服纳米级二硼化钛多晶体颗粒传统制备方法难以调控的不足,能够投入低成本、高产率的大范围工业化生产之中[5]。而王晓玲[6]在其研究成果中提出,通过调节熔盐介质中金属热还原法的原料种类及配比、熔盐组成等条件,可生产出不同纯度及形貌的TiB2粉体,这种方法更进一步实现了纳米颗粒尺寸的细化。
硼化钛通常是指硼和钛所形成的化合物,其存在形式多种多样,目前已知的包含TiB2、TiB、Ti3B4、Ti2B等形态,不同形式下的晶体结构也各不相同。二硼化钛(TiB2)作为其中化学性质最为稳定、应用最为广泛的一种化合物,也是本文的主要研究对象,它的密度为4.52 g/cm3,熔点为2980℃,热压硬度为1800~2700 kg/mm2,室温下导电率为1510-6Ω•cm,热膨胀系数为8.110-6m/m.k,抗弯曲刚度为450-575MPa,硬度为24Gpa[7],这些性质使得二硼化钛在新型材料、机械加工工艺、冶金、军事设备等工业领域都发挥着重要作用。童豪[8]等人利用二硼化钛导电性良好的物理性质,将其添加至导电性能较差的聚酰亚胺中,制备PI/TiB2复合材料薄膜,改善了材料的热稳定性和力学性能,使得实际应用的安全性有所提高。唐海[9]等人的研究结果表明TiB2作为添加剂能够促进浇注料的致密化,使其强度等力学性能得到大幅度提高。
二硼化钛表现出的优良性能与其晶体结构及电子结构密切相关。二硼化钛为C32型结构的六方晶系准金属化合物,结构中硼原子层和钛原子层交替堆叠形成网状结构,其成键类型也十分复杂,这种成键方式造成二硼化钛晶体结构中层内化学键强于层间化学键,故而其宏观上具有弹性各向异性的特征,且它在正应力作用下的抗变形能力大于在剪应力作用下的抗变形能力[10]。由此可见,较低的剪切强度使二硼化钛的应用受到限制,所以对其剪切变形机制的研究十分重要。因此,本文将采用第一性原理计算方法研究二硼化钛在不同滑移系中的剪切强度,进一步探究其剪切变形机制。
1.2 国内外研究现状
目前硼化钛的相关研究主要集中于对其晶体结构、力学、热力学、电子性质进行理论仿真计算。第一性原理基于量子力学理论,仅通过多粒子体系自身的固有属性,由薛定谔方程得到基本性质参数,计算精确度较高,现已被广泛用于分析材料的基本性质[11]以及在外载荷作用下的力学行为和变形机制。TiB2中不仅包含 Ti2 与 B-混合键、 B-与 B-间的σ键,还存在B-2pπ电子构成的离域大π键,钛原子层中Ti-Ti键的共价键级小,结合力弱;硼原子层中B-B键的共价键级大,结合力强;钛原子与最邻近硼原子间的Ti-B键的共价键级较大,结合力较强,而与次邻近硼原子间不存在键合,结合力较弱[12] 。Sun L[13]等人通过分析硼化钛的弹性常数,说明其具有各向异性的弹性性质,它的层内化学键比层间化学键强,并且硼原子通过sp2杂化剪切价电子,形成了由六边形网络组成的分层子晶格 。Tian J[14]等人系统研究了高温高压对硼化钛晶体结构、力学和热力学性质的影响,结果表明,硼化钛在压力下力学性质稳定,其体积模量、剪切模量和刚度随着压力的增加而提高,因此压力有利于提高硼化钛材料的塑性。Zhang X[15]等人研究了部分过渡金属二硼化物的理论强度,结果表明TiB2在(0001)晶面上具有最低剪切强度,同时基于硼六边形相对刚度所获得的B-B键长度可以作为表征二硼化物对基平面滑移或棱柱平面滑移的择优取向性的指标。Panda K B[16]等人采用全势线性缀加平面波方法(FLAPW)及广义梯度近似方法进行TiB2单晶独立弹性常数及多晶模量的计算,并分析了原子弛豫产生的效应、结构内部化学键及电荷密度分布,结果表明,变形后的内部原子弛豫对单晶弹性常数有显著影响,TiB2具有各向异性弹性特征,B-B共价键是其中最强的化学键,也是弹性常数最大值C11的主要来源。上述研究均对二硼化钛的基本性质及滑移系进行了详细的分析,但缺少对于微观层面变形机理的描述,因此本文着重于此进行分析。
1.3 研究内容
本文利用第一性原理软件Vienna ab-initio Simulation Package(VASP)分析二硼化钛的基本材料性质,并研究它在不同方向的剪切载荷下的力学行为及对应的微观变形机制,主要研究内容为:
1.硼化钛晶体结构
利用Material Studio软件,根据空间群、原子空间坐标、晶格常数等参数,建立硼化钛三维立体晶体结构模型。
2.硼化钛的力学性质和电学性质
首先利用VASP软件,采用投影缀加平面波赝势,交换关联函数为广义梯度近似方法下的PBE形式,设置一系列能量收敛性参数,结构弛豫的计算采用共轭梯度法,布里渊区k点的产生采用Monkhorst-Pack方法,对硼化钛初始结构模型进行几何弛豫,使得体系处于最低能量状态,得到优化后的模型。然后对晶格常数优化后模型展开计算,获得弹性常数、电子态密度等重要的材料性质参数,进而分析硼化钛在基态下的力学性质和电学性质。
3.硼化钛的剪切变形机制
分析硼化钛的晶体结构,了解其在剪切外荷载下的滑移系。在此基础上,对硼化钛进行剪切模拟,得到应力-应变曲线,能量-应变曲线、晶格常数-应变曲线和电子局域函数图等,进一步分析其相关变形行为以及对应的微观变形机制。
1.4 预期目标
本文通过VASP软件对二硼化钛晶体进行优化,然后对优化后的模型展开静态计算,得到弹性常数、弹性模量、电子态密度等重要材料参数,由此分析其电、力学性质。此外,对二硼化钛体系进行剪切变形模拟,从微观层面解释它的剪切变形机制。
第2章 第一性原理
2.1 第一性原理简介
第一性原理是属于原子尺度范畴的计算方法,它仅借助材料的基本物理常量、构成成分以及结构特征,通过近似简化进而获得体系的基本性质及行为状态,其主要理论基础为密度泛函理论,实际运算主要通过计算机程序进行,既可应用于对已有体系结构性质的具体描述,也可以进行新型特殊材料的设计。密度泛函理论的核心假设是一个多粒子体系的性质仅与其粒子密度空间分布相关,在此框架之下,复杂体系波函数求解十分困难的问题得到解决,运用第一性原理进行材料基本物理性质精确、高效率的计算成功得到实现。
2.2 波函数及薛定谔方程
第一性原理是在量子力学的基础上衍生发展起来的理论体系,而在量子力学当中,微观粒子及其体系的运动状态是通过以时间及位置为基本变量的波函数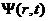 进行表达的,其中比较特殊的为定态波函数
进行表达的,其中比较特殊的为定态波函数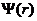 ,它仅与空间位置有关。自由粒子波函数的数学表达式为
,它仅与空间位置有关。自由粒子波函数的数学表达式为
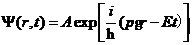 (2.1)
(2.1)
1926年,薛定谔方程的发表拉开了量子力学的帷幕,其本质为微观粒子波函数满足的波动方程。当质量为m的自由粒子不受外力作用时,其波函数满足以下薛定谔方程
| (2.2) |
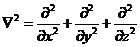 (2.3)
(2.3)
当速度较低的非相对论粒子受到势能函数为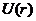 的外力场作用时,薛定谔方程的形式变为
的外力场作用时,薛定谔方程的形式变为
此时,能量 | (2.4) |
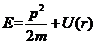 (2.5)
(2.5)
如果粒子处于在不随时间变化的稳定势场,进一步引入哈密顿算符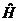 及能量算符
及能量算符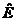 ,
,
可得如下形式的定态薛定谔方程
| (2.6) |
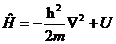 (2.7)
(2.7)
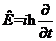 (2.8)
(2.8)
对以上方程式(2.4)运用分离变量法,将波函数转换为仅含时间变量的函数与仅含位置变量的函数之乘积
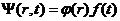 (2.9)
(2.9)
进行求解得到其本征函数表达形式为
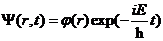 (2.10)
(2.10)
以上均为单个粒子的运动相关方程,若将其扩展至含有N个粒子的体系,则体系的薛定谔方程变为 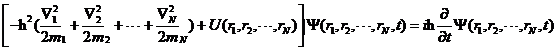 (2.11)
(2.11)
2.3 近似简化方法
2.3.1 Born-Oppenheimer近似
Born-Oppenheimer近似将体系波函数的求解分离开来,单独进行电子波函数和原子核波函数的计算。由于原子核在质量及尺寸上远大于电子,而其运动速度远小于电子,因此,当研究电子运动时,认为原子核处于静止状态,电子绕核运动,考虑其势能及动能;当对原子核状态进行分析时,认为电子能够在极短的时间内迅速完成运动,故而周围电子的具体空间分布情况无需考虑,波恩和奥本海默假设计算时只有原子核的势能对波函数产生影响。这一近似处理实现了原子及电子间坐标的相互独立,不同原子核间的相互作用也可单独进行处理,极大地降低了计算复杂度。
在此近似条件下,体系总波函数满足
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: