摘 要

本文主要对磁活性弹性体的驱动方式进行了分析讨论，既通过理论计算给出定量地分析也通过有限元仿真给出了定性的理解。对于椭球形的磁性颗粒在磁场中受到磁力矩的作用发生旋转进而引起基体的变形的行为，通过计算、推导、演化，最终对于磁力矩得到了较为精确的数学表达式，得出磁力矩与颗粒形状、磁场、颗粒以及基体材料属性之间的关系。为以磁活性弹性体为代表的磁性智能复合材料的制备、操纵提供了理论依据。然后又通过有限元分析了几种铁磁性椭球体颗粒在平行磁场中的非均匀磁化、磁场分布、磁力分布、磁力矩数值、周围基体的变形以及应力分布。得出了磁性椭球形颗粒在磁场中所受力矩与颗粒形状之间的关系。

关键词：磁活性弹性体、磁力矩、椭球形颗粒、有限元分析

Abstract

In this paper, the driving mode of Magnetoacitve Elastomers is analyzed and discussed. Quantitative analysis is given by theoretical calculation and qualitative understanding is given by finite element simulation. For the deformation of the matrix caused by the rotation of the ellipsoidal magnetic particles under the action of magnetic moment in the magnetic field, a more accurate mathematical expression of the magnetic moment is obtained through calculation, derivation and evolution, and the relationship between the magnetic moment and the shape of the particles, magnetic field, particles and the properties of the matrix material is obtained. It provides a theoretical basis for the preparation and manipulation of magnetic intelligent composites represented by magnetically active elastomers. Then the non-uniform magnetization, magnetic field distribution, magnetic force distribution, magnetic moment value, deformation of surrounding matrix and stress distribution of several ferromagnetic ellipsoidal particles in parallel magnetic field are analyzed by finite element method. The relationship between the force moment of magnetic ellipsoidal particles in magnetic field and the shape of particles is obtained.

Key words: Magnetoacitve Elastomers, Magnetic Torque, Ellipsoid Particle, Finite Element Analysis

目录

第一章 绪论 1

1.1磁活性弹性体简介 1

1.2磁活性弹性体的磁力行为与局部变形 1

1.3目前国内外研究概况 2

1.4 本文研究的内容及目标 3

第二章 颗粒磁力矩作用对局部变形的影响 4

2.1 理论分析 4

2.1.1 颗粒的磁能与磁力矩 4

2.1.2 刚体颗粒旋转带动基体变形及其弹性储能 8

2.1.3考虑磁力矩效应的力磁耦合行为分析 9

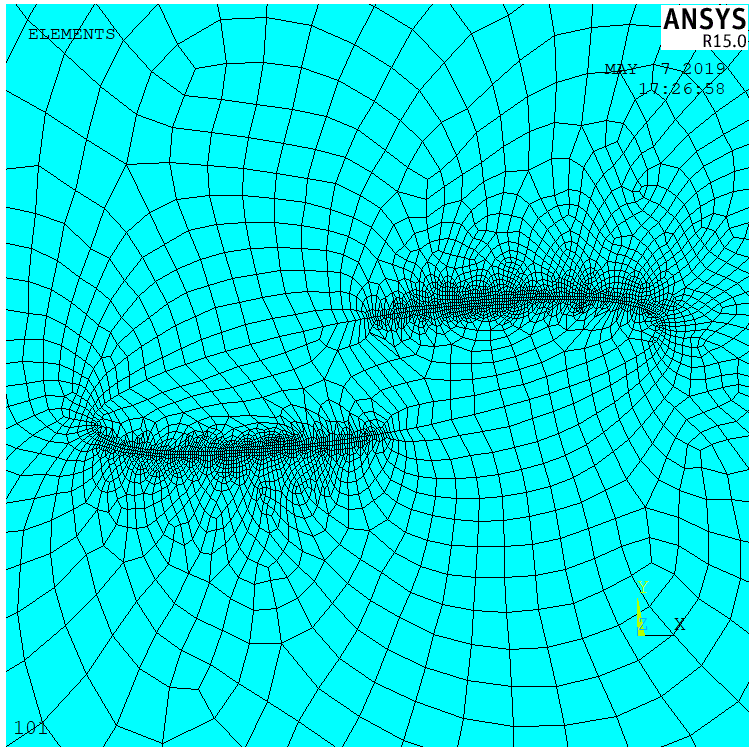
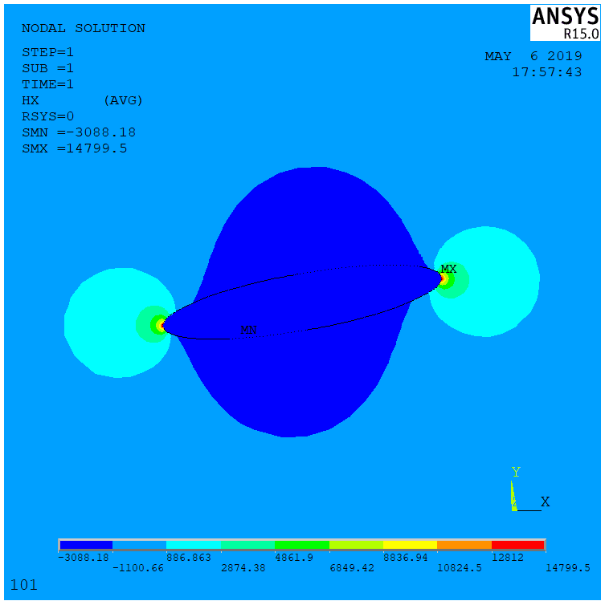
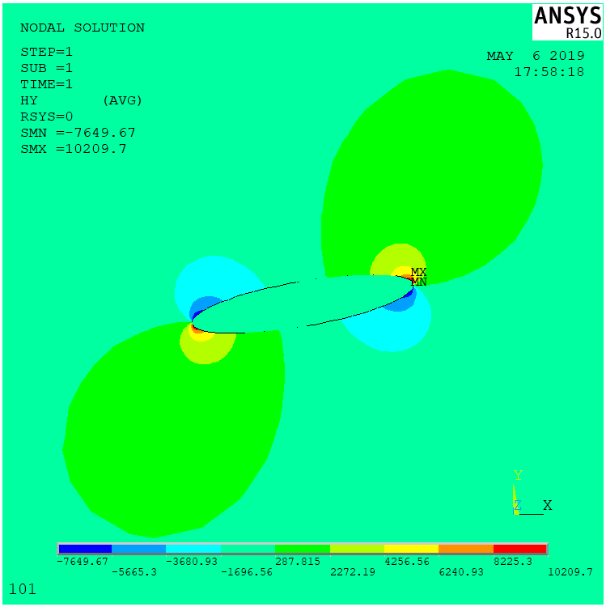
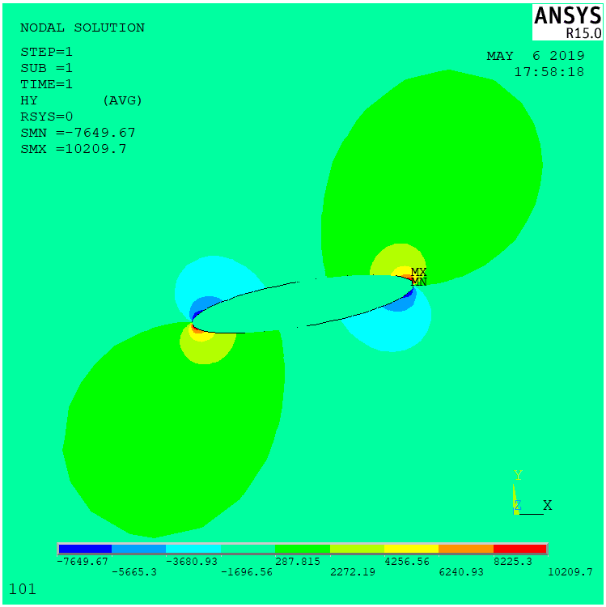
2.2 数值模拟 9

2.2.1 数值建模流程 10

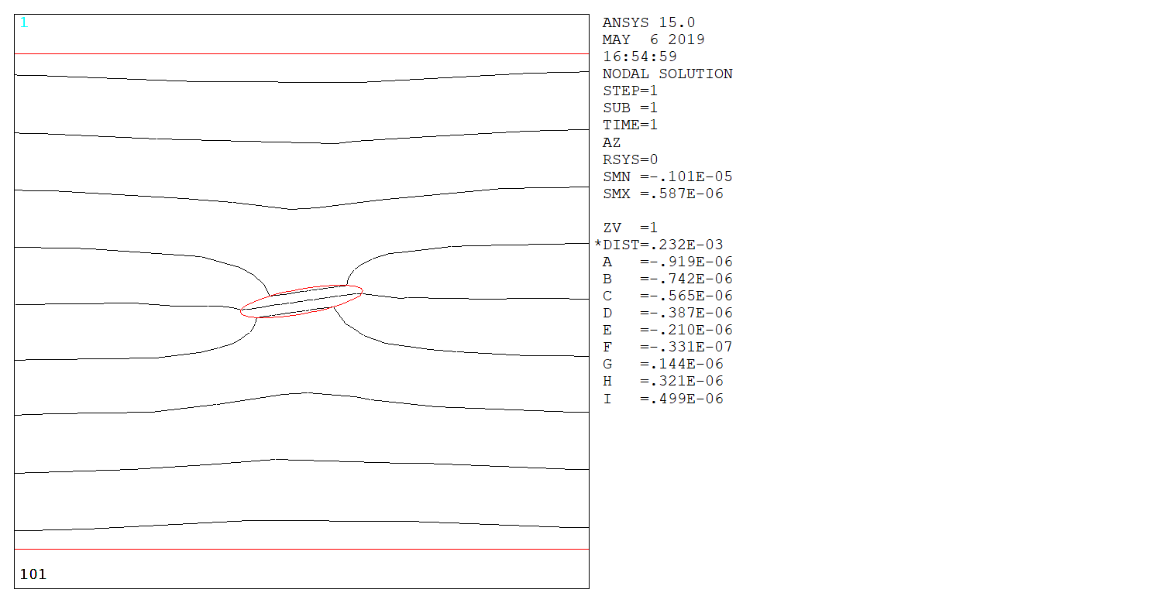
2.2.2 算例与结果分析 15

第三章 结论 23

3.1理论推导结果分析 23

3.2有限元仿真结果分析 23

参考文献 25

致谢 27

第一章 绪论

1.1磁活性弹性体简介

随着现代工业的迅猛发展和当代科技的飞速进步，人工智能已经成为脍炙人口的主题，在此潮流推动之下，柔性智能复合材料因其与生物机体非常接近的材料属性以及非凡的智能控制方式而倍受关注。其中，以磁活性弹性体(Magnetoacitve Elastomers, MAEs)为代表的磁性颗粒增强智能复合材料，因其优良的磁弹性性能、丰富的磁致响应和非接触的控制模式成为近年来的研究热点^[1-3]。

磁活性弹性体（MAE）是一种具有明显磁流变效应的复合材料^[4]，这种复合材料都以软物质为基体以磁性材料为夹杂。当磁性颗粒被磁场磁化时，它们能够在磁场的作用下在基体中移动。有关研究表明，在MAE中观察到一个相对延伸率高达100%的异常大磁致伸缩，弹性模量异常增加，磁场中的介电常数显著增加^[5,6] 。已有研究表明，该类材料除了可以产生磁致伸缩这类均匀变形的行为，更是可以通过特殊微结构设计实现磁致弯曲等非均匀变形行为^[7]。

磁活性弹性体应用极其广泛，在流变学、生命科学、光学和建筑材料等方面都有很强的利用价值。由于磁活性弹性体反应灵敏，形状改变易于控制、变形可逆的优良特点，可以被用作机械减震、液体流动密封、人工肌肉等^[7]。

1.2磁活性弹性体的磁力行为与局部变形

磁活性弹性体丰富的磁致力学响应行为是内部磁力、微结构演化与变形三者相互作用的宏观表现。复合材料的内部磁力主要来源于磁化颗粒：在磁场作用下，一方面微磁结构引起的铁磁性与形状不对称引起的偏磁性会使颗粒受到磁力矩的作用，另一方面磁化产生的扰动磁场使得分布颗粒间存在磁性相互作用力^[7,9]。当磁力离散地作用于磁性颗粒增强复合材料内部时，形成所谓的磁致应力^[10]。该应力不仅可以协助基体抵抗或促进机械荷载带来的变形，在宏观上呈现出磁流变效应，而且可以带动周围基体产生变形，在宏观上产生磁致应变响应^[11]。

特定微结构的磁性颗粒增强复合材料在外加磁场作用下产生非均匀变形的根本原因在于：颗粒分布、取向等微结构的不均匀性，会导致内部的磁场分布不均，颗粒系统因此会受到非均匀的磁力作用，促使复合材料产生非均匀变形；与此同时，颗粒分布、取向等微结构会发生演化。

磁活性弹性体继承了磁流变液的磁敏特性, 但是其工作原理和应用范围与磁流变液相比都有了很大的差异. 磁活性弹性体的磁性颗粒在制备完成后就被固化在基体中, 施加磁场后颗粒无法自由移动, 无法发生磁流变液的“相变" 现象, 因此其力学性能也无法像磁流变液那样随着磁场的改变发生巨大的变化^[2]。

1.3目前国内外研究概况

对外加磁场敏感的材料越来越受到工业界和研究人员的关注和应用。嵌入在基底内的可磁化粒子的重新排列会导致材料变形并改变其固有特性。为了更好地预测材料的性能，需要进一步了解磁负载下颗粒的影响。F. Vogel等人研究了两种不同的方法来确定在一个通用领域内产生的磁力和扭矩。对这两种方法进行定性和定量比较，提出了一种比另一种更适合使用的方案。还描述了一种计算产生磁力矩的方法。这些后处理过程利用了大变形磁弹性问题的磁标量势公式的结果，在几个例子中演示了它们的应用，这些例子涉及嵌入在载体矩阵中的单颗粒和双颗粒系统。结果表明，在给定一组选定的边界条件下，作用于颗粒上的磁力和转矩受其形状、尺寸和在载体内的位置的影响^[12]

G. Ethiraj等人提出了一种方法来模拟磁流变弹性体(MRES)在有限应变下的宏观磁弹性模型，磁流变弹性体的结构以模块化的方式来描述基于微机械的成分。考虑到微观尺度上的复合性质，他提出了一种本构关系式，用于为磁化刚性铁颗粒的能量和可变形聚合物网络的弹性能提供两个微观结构的内核。后者是通过变形梯度的弹性-磁乘积分裂来实现的。根据复合材料的空间磁化强度矢量，提出了一种包含磁致伸缩变形的左分解方法。将标准各向同性链统计量映射为各向异性统计量。该方法允许采用模块化格式的聚合物微机械各向同性网络模型，并将其应用于各向异性耦合磁力学响应。特别是。这样的公式允许包含基于网络的弹性的微型球体模型。这已成功地应用于橡胶类聚合物的建模。讨论了有限磁弹性变分公式中统一建模结构的细节. 并给出了耦合问题的有限元素实现方法，并通过求解面向子的边值问题，展示了该问题的建模能力^[13]。

Evan Galipeau等人研究了具有周期性和随机分布的圆形和椭圆形纤维的磁活性弹性体（MAEs）的行为。对于具有周期性微观结构的MAE，建立了有限元模型，确定了矩形和准六角形单元的MAE的局部场和有效特性。对于具有随机微观结构的MAE，利用最近发展的理论推导出有效响应的封闭式表达式。特别是，确定了在磁场存在下对纯剪切载荷的响应，这两个磁场都与纤维的几何轴对齐，并研究了变形、浓度、颗粒形状和分布对复合材料的磁致伸缩、驱动应力和磁感应刚度的作用。结果表明，在浓度范围内，耦合效应为二阶。这与这些效应主要是包裹体之间相互作用的结果是一致的。还明确地证明了，当在对准载荷条件下，这些MAE的磁机械耦合不仅取决于磁化率，而且，至关重要的是，取决于其变形的导数。因此，发现磁弹性效应可能是非常不同的，即使对于具有类似有效磁化率的复合材料也是如此^[14]。

Oleg V等人讨论了软磁弹性体中的磁致伸缩效应：在无机械载荷的均匀磁场作用下样品的拉伸与收缩。定性分析表明，电场对介质有双重影响，其中一种机制在宏观尺度上起作用，另一种机制来自细观过程。从本质上讲，后者是由铁磁颗粒组合中存在的短程空间有序的“结构”所定义的。利用数值模拟方法对这一结论进行了图解说明。首先，它是在一个充满线性可磁化粒子的二维弹性阵列上完成的。结果表明，确实存在着控制复合材料中磁致伸缩的符号和大小的簇。换言之，具有相同基质/填料含量的两种复合材料，其性能可能因其介电尺度结构而不同。此外，为了得到更真实的描述，模型被扩展到一个随机分布在弹性矩阵中的球形粒子的三维阵列。虽然一般结论成立，但定量结果相差很大^[15]。

开发具有复杂的操作灵敏度和行为自适应调节功能的传感器系统是一个实际的科学和技术挑战。像磁敏弹性体（MSE）这样的智能材料被认为是解决这一问题的一个潜在方案，因为它们的机械性能可能受到外部磁场的控制。T.I.Volkovaa研究了均匀磁场作用下含MSE磁性软粒子的弹性和阻尼特性。在测量固定梁自由弯曲振动的第一特征频率的基础上，从理论上和数值上分别计算了固定梁的有效杨氏模量。结果表明，该参数和光束的第一特征频率随外加磁场的大小而单调增加。研究结果旨在研制一种具有自适应磁控灵敏度范围的加速度传感器，用于环境外部机械刺激的检测^[16]。

Karl A.Kalina等人对具有结构化和非结构化颗粒分布的磁流变弹性体的变形相关行为进行了数值研究。为此，进行了有限元模拟，以计算不同试样的有效磁化强度和宏观驱动应力，这些试样具有真实的微观结构和不同的机械预载荷。由于所提出的微尺度模型是基于磁力学边值问题的连续公式，因此在微结构中可以明确地解决局部磁场和机械场。有限应变的考虑导致了耦合场问题的有限元实现，并给出了一致线性化方案。为了更好地理解实际试件的变形依赖行为，对链状结构进行了研究。结果表明，链状结构中各组分之间的相互作用会产生不同的材料响应，这取决于它们的位置。这些发现被用来解释机械预载荷对具有结构化和非结构化粒子排列的样品行为的影响。我们的所有研究结果都与对包含结构化颗粒分布的磁流变弹性体进行的实验研究结果一致^[17]。

1.4 本文研究的内容及目标

磁活性弹性体的有效变形行为是通过局部磁场控制引起的局部变形积累获得，因此有效的控制磁活性弹性体的磁控力学行为，其内部的微观结构设计至关重要。若要合理设计材料的内部微观结构，就需要对微观机制开展基础性研究。本论文以理论建模为主体，辅以有限元分析验证这种模型在几种特定情况的案例，重点分析非球形颗粒因其自身的非均匀磁化带来的磁力矩效应所引起的旋转带来的周围基体变形规律，初步建立夹杂颗粒形状、颗粒和磁场偏角与颗粒所受磁力矩间的关系，进而可以进一步的分析材料的有效变形行为。

第二章 颗粒磁力矩作用对局部变形的影响

2.1 理论分析

本节通过对磁活性弹性体中颗粒磁力矩作用的研究讨论分析，得出了关于所研究椭球体颗粒储存的的磁能及其受到的磁力矩的表达式，结合椭球体颗粒在基体中所固有的弹性恢复力矩的表达式，进而得出颗粒磁力矩作用对局部变形影响的规律。

2.1.1 颗粒的磁能与磁力矩

磁性椭球体颗粒在磁场中，由于受到磁力矩的作用，使颗粒旋转到能量最低的地方。在这种情况下，磁力矩是以Nm为单位表示的

（2.1）

同时，磁力体力扭矩（）可以等效为由施加在力臂上的磁力产生。在这种情况下，磁体扭矩可以用施加于颗粒体的磁力（）和该力作用点距离支点（旋转点）的位移矢量r表示为

(2.2)

在磁力矩作用下，颗粒体具有一定能量的永磁偶极子。在存在局部磁场的情况下，颗粒的永久偶极子与局部磁场的任何偏差都将以较高的能量状态（）存在，根据

(2.3)

这里，是颗粒磁矩，以A为单位，B是以T为单位的磁通量密度。磁矩近似为，其中M是颗粒体的磁化强度，V是颗粒体的体积。颗粒体的磁化方向是由初始磁化过程中材料的排列决定的，通常对应于某个首选的物质的原子晶体中的转轴。其中因此

=- (2.4)

在磁性颗粒体中，颗粒材料内没有永久磁偶极子，在局部磁场下提供转矩。对于非磁性介质中的顺磁性颗粒，磁化强度以低磁性为线性尺度。这里是粒子的形状校正磁化率，例如球形校正磁化率为。在较高强度的磁场下，顺磁材料的自旋最大限度地耦合，并在饱和磁化强度(即)达到上限。为了充分描述在这种系统中的顺磁性颗粒的磁化，可以使用Langevin等式：。这里，且。在这种情况下，顺磁偶极子上的转矩平衡。

(2.5)

各向同性顺磁性材料不会因其偶极矩与局部磁场的相互作用而产生磁矩。然而，如果存在几何或磁各向异性，则仍然可能存在不同类型的扭矩。

如果顺磁性颗粒具有几何各向异性，则颗粒排列的能量与最小化磁化体的内部阻力。由局部原子自旋产生的内部场（）被邻近的原子感受到。如果附近的原子位于磁场的方向上，原子的旋转就一起工作，以增加内部磁场。然而，如果附近的原子垂直于磁场的方向，则原子的自转相互作用，产生退磁磁场，从而减少内部磁场。顺磁性物体的内部磁场可以确定为

（2.6）

式中G是一个退磁因子，它完全依赖于颗粒的几何形状以及颗粒与其所处的场成的角度。如果这个颗粒是球形的，那么它与磁场的关系是完全对称的。对于非球形颗粒，G需要针对每个可能的方向分别确定。许多杆状，纤维，针和病毒可以被近似看作扁长球体（长轴是a，两个短轴是b），当一个方向的半径很大（a/bgt;5）,在这种情况下，长轴完全对齐时和长轴垂直于局部场时的退磁系数可分别近似为^[7]。颗粒在每个可能的方向上存在的能量可以通过内部场中每个原子自旋的能量对整个体积上积分来解决。对于低强度场，可以表示为

（2.7）

因此，方程（1）顺磁性的力矩在一个扁长的椭球体上变成

(2.8)

另一方面，假设椭球体颗粒两个长轴为b，一个短轴为a，当长轴与短轴比较大（b/agt;5）时，可近似为扁平球体。在这种情况下，退磁系数可以确定为^[7]。颗粒的能量和力矩可以通过将粒子整个体积内的内场中每个原子自旋的能量积分为

（2.9）

(2.10)

在扁长的和扁平的顺磁性颗粒都有的情形中，颗粒的长轴与此处场的方向偏离角时，磁力矩最大。

相反，磁力产生的力矩是由磁分布力产生的，磁力作用点相对于支点的力臂。在这种情况下，磁性体扭矩（）源于施加在颗粒体上的磁力。施加在物体上的磁力需要磁场梯度并产生扭矩

(2.11)

磁体力矩通常要求将磁力与颗粒的旋转尺寸相对于颗粒的体积进行积分。许多磁性聚合物薄膜的研究往往由于磁体力矩的存在和膜的几何力矩的存在而变得复杂。

本文所计算的模型是，给夹杂着磁性颗粒（顺磁性颗粒，体积为V，其内部场强为）的非磁性软物质施加一个磁场强度为的磁场，这里只研究磁场，因此忽略热损失和其他影响，如热搅拌和重力。同时为了数学上的简单性，假设颗粒和基体两种介质是线性的，且基体是各向同性材料，颗粒只有磁性上是各向异性的，颗粒内部的储存的磁能变化可以用下式计算

(2.12)

其中，分别为颗粒和基体的磁导率。当U为正时，场中的储存能量减小，当U为负时，场中的储存能量增加。利用该方程，导出机械力及其影响，并对其意义进行了定量描述。

在两种介质的边界上，磁通量通常是折射的，颗粒为介质1，基体为介质2，和分别是两种介质内部的磁场强度的切向分量，以及和为其二者法向分量，他们遵循这种关系。

（2.13）

（2.14）

从等式（2.12），（2.13）可以得出，对于场的切向分量引起的储能变化为

（2.15）

因此作用在边界上的力为

（2.16）

由于，因此边界上的机械应力为

（2.17）

同样，对于场的法向分量引起的边界上机械应力为

（2.18）

球体内部的磁场强度为

（2.19）

代入等式（2.12）并积分，可得球形颗粒存在，引起的储能变化为

（2.20）

r是球性颗粒的半径。而对于和球形颗粒同体积的椭球体颗粒，椭球体内部的磁场强度为

(2.21)

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：