摘 要

宇宙学中，哈勃常数H₀是一个非常重要的参数。哈勃常数由哈勃定律给出，这是上个世纪天文学中最为伟大的发现之一。由于近些年许多H₀ 的测定结果的数值总体的一致是令人十分满意的，以至于近来目前对H₀的测量估计在局部上的争议却显得越来越重要。

本文借助公共可用包CosmoMC，使用蒙特卡罗方法（Monte Carlo Simulation，简称MC）和马尔科夫链（Markov Chain ，也简称MC），对52组哈勃参数H(z)进行数值模拟和参数边缘化处理，分别在平直空间∧CDM模型、非平直空间∧CDM模型和平直空间ωCDM模型这三种模型下测量在中间红移0.07lt;zlt;2.36范围内，进行参数边缘化的限制以确定如今的哈勃常数H₀。三个模型分别给出（1σ误差和2σ误差）：、和。这些测量的H₀值与最近给出宇宙中确定的较高的值更为一致。三种模模型给出的数值相互比较契合但与Plank 2015项目的宇宙微波背景数据给出的H₀=67.8±0.9 km·s⁻¹·Mpc⁻¹对比差异是并不小。对这样的差异进行了分析，所得结果对于CDM模型的扩展和发展具有重要的指导意义。

关键词：暗能量；宇宙学参数；哈勃定律；哈勃常数

Abstract

In cosmology, the Hubble constant H₀ is a very important parameter. The Hubble constant, given by Hubble's law, is one of the greatest discoveries in astronomy of the last century. Due to the overall agreement of the values of many H₀ measurements in recent years, it is very satisfactory that the local disputes on the measurement and estimation of H₀ become more and more important. In this paper, with the help of a public available packages CosmoMC , using Monte Carlo method(MC) and Markov Chain (MC), H (z) parameters of 52 Hubble marginalisation of numerical Simulation and parameter processing, respectively, in the spatially-flat ∧CDM model, the general (non-flat) ∧CDM model and the spatially-flat ωCDM model under these three model measurement in the intermediate redshift 0.07 lt; z lt; 2.36 within the scope of marginal limit parameters are carried out to determine the Hubble constant H₀ now. Three models are given (1σ and 2σ): ：、 and . The H₀ values from these measurements are more consistent with the higher values recently given in the universe. The values given by the three models agree with each other but are not too small compared with the results of the Plank 2015 CMB data, which showed H₀=67.8±0.9 km·s⁻¹·Mpc⁻¹.The differences are analyzed, and the results have important guiding significance for the development of CDM model.

Key Words：Dark energy; Cosmological parameters; Hubble's law; The Hubble constant

目录

第1章 绪论 1

1.1 哈勃常数的发现 1

1.2.1 哈勃常数的历史 1

1.3哈勃常数的近况 2

第2章 ∧CDM模型和ωCDM模型 5

2.1 CDM的意义 5

2.2 ∧CDM和ωCDM 11

第3章 统计分析与总结 12

3.1 数据来源 12

3.2 统计与分析 13

3.3总结与展望 17

参考文献 18

致谢 20

第1章 绪论

宇宙学中，哈勃常数H₀是一个非常重要的参数。哈勃常数由哈勃定律给出，这是上个世纪天文学中最为伟大的发现之一。

1.1 哈勃常数的发现

在1929年，埃德温·哈勃(Edwin Hubble)开展了对河外星系的视向退行速度与距离的关系的研究。哈勃使用当时仅有的能使用的46个河外星系的视向退行速度，并且46个中仅有24个能够推算出距离，其中作为样本。样本中的星系的视向退行速度最高的也不超过1200km·s^-1，然后设法合理地估计了星系与地球之间的对地距离之后，哈勃得出河外星系的视向退行速度与距离之间大致的线性正比关系。而这一线性正比关系，此后便称为哈勃定律，其中v_f为对河外星系的视向退行速度，d为对地距离，H₀就是著名的哈勃常数。实际上，当时哈勃推导出的河外星系视向退行速度与距离的线正比关系结果并不是十分清晰，个别星系的数据与结论的拟合存在比较大的弥散。尽管如此，该结论仍然在当时造成了整个学界的轰动，因为一直以来，学界都认为宇宙是静止不动的，但若考虑红移是由星系视向运动的多普勒效应引起的，那么该结论则表明，星系正在远离我们，而且距离越远的星系其远离的速度越大。在广义相对论出世之后，哈勃定律通常就被解释为宇宙膨胀的必然结果。哈勃定律的发现推翻了长期以来学界所默认的宇宙静止模型，随之揭示出的是一个宇宙膨胀模型，因此其对于推动了现代宇宙学的发展具有重大作用。

1.2.1 哈勃常数的历史

虽然哈勃常数是最能够被测量的宇宙学常数之一，但是H₀的一致值却是在哈勃第一次测量之后的70多年之后才开始出现。下面的图1.1显示了哈勃常数的测定值随时间演变的历史，这是径向速度和距离之间的比值，单位是千米/秒/百万秒（km·s⁻¹·Mpc⁻¹），因为它是由Lemaitre Georges，H. P. Robertson和Edwin Hubble在1920年代后期首次确定的。值得注意的是，第一点实际上是来自G.Lemaitre于1927年发表的一篇论文，该论文基于哈勃导出并发表的星系距离导出的。第二个来自H.Robertson，也主要基于哈勃的数据。哈勃自己终于在1929年以500 km·s⁻¹·Mpc⁻¹的速度进行了发表。此外，荷兰天文学家Jan Oort很早就认为哈勃的规模出现了问题，并且发布了290 km·s⁻¹·Mpc⁻¹的值，但这基本上被遗忘了。

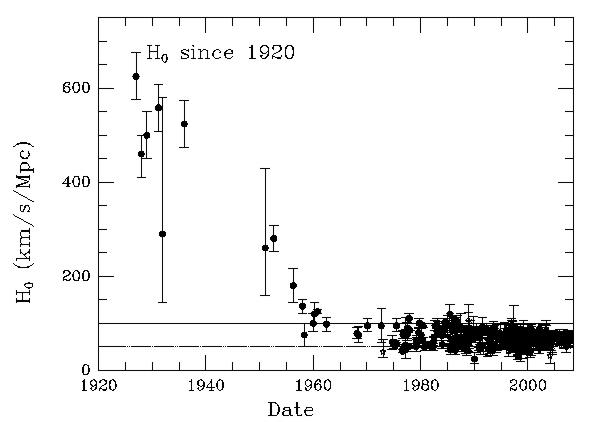
图1.1 哈勃常数的测定值随时间演变的历史

哈勃的价值的第一次重大修订是在上个世纪五十年代由于W. Baade发现了人口II星。接下来是对混淆等的其他修正，在1960年代早期几乎将接受的值降低到大约100 km·s⁻¹·Mpc⁻¹。该图显示了现代（哈勃空间望远镜，Hubble Space Telescope，HST）的测定结果，包括引力透镜作用的结果和Sunyaev-Zeldovich效应作用的应用。注意最近的收敛值接近65 ± 10 km·s⁻¹·Mpc⁻¹（每百万光年约13英里每秒）。

1.3哈勃常数的近况

2001年wendy freeman等人就把H₀=72±8 km·s⁻¹·Mpc⁻¹（一个σ误差包括系统误差），作为哈勃太空望远镜重点项目H₀值的合理总结。同年（2001），J. Richard Gott III等人将中位数统计应用与由John Huchra编制的包含331组H₀数据的汇编列表^[1]，并得出H₀=67±3.5 km·s⁻¹·Mpc⁻¹。在接下来的十年中，中位数统计不断被应用与John Huchra编制的更大的H₀数据汇编列表。2003年Gang Chen等人使用461组数据得出H₀=68±3.5 km·s⁻¹·Mpc^{−1 [2]}。2011年Gang Chen和Bharat Ratra使用553组数据得出H₀=68±2.8 km·s⁻¹ mpc^{−1 [3]}。

近些年来许多H₀的测量结果和这些结果在大致上是一致的。例如，2013年，G. Hinshaw等人^[4]通过威尔金森微波各向异性探测器（Wilkinson Microwave Anisotropy Probe ，WMAP)最后得出H₀=70.0±2.2 km·s⁻¹·Mpc⁻¹。同年，Jonathan L. Sievers等人^[5]通过Atacama宇宙学望远镜和长达7年的宇宙微波背景各向异性数据给出H₀=70.0±2.4 km·s⁻¹·Mpc⁻¹（于2015年Éric Aubourg等人^[6]；另见于2015年Ross等人；2016年L’Huillier和Shafieloo两人^[7]；于2016年Jose Luis Bernal等人^[8]；于2016年Vladimir V. Luković等人^[9]） 而且由重子声振荡（BAO），la型超新星和宇宙微波背景的数据给出H₀=67.3±1.1 km·s⁻¹·Mpc⁻¹。2015年，Plank 2015项目的宇宙微波背景数据（cosmic microwave background，CMB）^[10]给出H₀=67.8±0.9 km·s⁻¹·Mpc⁻¹。

虽然这些结果的一致性是令人十分满意的，但近来一些对H₀的测量估计在局部上存在更大差异。Adam G. Ries等人在2011年给出H₀=73.8±2.4 km·s⁻¹·Mpc^{−1 [11]}而George Efstathiou于2014，他认为H₀=72.5±2.5 km·s⁻¹·Mpc^−1[12]是更好的表示。W. L. Freedman等人在2012年给出H₀=74.3±2.1 km·s⁻¹·Mpc^−1[13]然而Adam G. Riess等人在2016年给出的H₀=73.24±1.74 km·s⁻¹·Mpc^{−1 [14]}。

如何去理解这种差异是很十分重要的。例如，H₀的值和不确定性会影响对其他宇宙学参数的观测限制（参见，如Lado Samushia等人与2007年^[15]；Gang Gang Chen等人于2016年^[16]）；根据目前的宇宙学数据，具有三种轻中微子的粒子物理标准模型更符合较低的H₀值，并且很难与较高的H₀值相协调；H₀值的局部和总体之间的差异也许表明∧CDM模型需要扩展（参见，如Di Valentino等人，2016年^[17]）。

这里我们使用哈勃参数h（z）（其中z是红移），加以测量以确定哈勃常数。H（z）数据以前也有用于约束其他宇宙学参数（参见，如Lado Samushia和Bharat Ratra于2006^[18]；Gang Chen和Bharat Ratra 于2011^[19]；Salvatore Capozziello等人于2014^[20]；Gang Chen等人于2015年；Xiao-Lei Meng等人于2015^[21]），包括测量早期非相对论物质主导时代和当前暗能量主导时代之间的宇宙学减速加速过渡过程的红移（Moresco等人于2016^[22];也同样见Licia Verde等人于2014^[23]）早期尝试从H（z）数据测量H₀。在这里，我们比Licia Verde等人（2014）^[23]使用更多的数据（本文使用了52组数据）来获得更高的红移，因此对H₀的限制更为严格。

我们发现，我们的H(z) 与H0值更符合用中值统计方法或CMB各向异性或BAO测量所确定的较低的值，也更符合只有三种光中微子并没有“暗辐射”的粒子物理标准模型的预测。影响哈勃常数H（z）测量的系统误差与影响CMB和BAO测量的系统误差有很大不同。十分有趣的是这四种技术产生的H₀值非常相似。

为了确定H₀，我们使用两种不同的暗能量模型∧CDM（Peebles于1984）和ωCDM（Peebles和Bharat Ratra于1988；Bharat Ratra和Peebles于1988）分析了Juan Magana于2018年发表论文中的h（z）数据^[24]。在所有情况下，我们都从一维似然度测量H₀，该似然度由所有其他参数的边缘化确定。（对其他参数的限制，如当前的非相对论物质密度参数，是相当合理的。）

在下一节中，我们将总结我们使用的模型以及CDM的参数。在第三章节，我们展示了我们的测定的H₀。最后的总结将在最后第三章的第三节。

第2章 ∧CDM模型和ωCDM模型

2.1 CDM的意义

∧CDM(∧冷暗物质)或称Lambda-CDM模型是一个参数化的宇宙大爆炸宇宙模型，模型中包含三个主要元素组成：第一，用希腊字母∧标记的宇宙学常数和暗能量；第二，理论上假设存在的冷暗物质（CDM）；第三，普通物质。在宇宙大爆炸假说理论中，∧CDM模型被称为是该假说理论的标准模型。不仅如此，∧CDM模型在宇宙大爆炸假说中也经常被称作索引模型，这是因为它尝试了解释对宇宙大尺度结构、宇宙微波背景辐射（CMB）以及宇宙加速膨胀的超新星观测。当前，该模型是能够对这些现象提供融洽合理解释的最简单模型。由于它是最简单的模型，它可以很好地解释宇宙的以下性质：

·宇宙微波背景的存在和结构

·星系分布中的大尺度结构

·氢(包括氘)、氦和锂元素的丰度

·从遥远的星系和超新星发出的光中观测到的宇宙加速膨胀过程

∧CDM模型假定广义相对论是宇宙学尺度上正确的引力理论。它出现在20世纪90年代末，作为一个宇宙学索引模型，在一段时间的研究后，不同的宇宙学性质的观测出现相互矛盾，并且没有对宇宙的能量密度的组成展示出令人满意的一致性。

∧CDM模型中的∧意思为宇宙学常数^[25]。它是解释当前宇宙观测到的加速膨胀的暗能量项。通常宇宙学常数用表示，它表示的是在当前宇宙中，暗能量在一个平直时空的宇宙的能量的占比。现在认为这个数值约为0.74，即表明当前宇宙中有74%左右的能量是以暗能量作为形式存在的。。

在罗伯森-沃克（R-W）度规^[26]下，从广义相对论的爱因斯坦场方程出发，可以得到R（t）的动力学方程（取光速c=1）

其中，p分别是宇宙质量的能量（质量）密度和压力，称为宇宙学常数。这个常数就是爱因斯坦1917年求解R（t）时，为了避免宇宙的坍塌或者膨胀，而人为地加上的一个常数。当时爱因斯坦认为，若没有这个常数，动力学方程表明，即宇宙空间整体加速度不为零，整个宇宙就不是当时学界认为的静态宇宙，而是一个动态的宇宙，这两者是相矛盾的，以至于爱因斯坦为了平衡引力效应的作用，加上了一个正号项，即宇宙学常数项。如此看来，宇宙学常数的物理意义理应是宇宙间的某种未知的斥力作用，而这种未知斥力就联系到了暗物质。实际上，截至目前已经有了足够多的证据表明了暗物质的存在，例如各种星系的质光比远大于1，漩涡星系平展延伸的转动曲线，更有十分著名的于星系团中广泛存在的并且已经观测证实的引力透镜现象。种种观测事实表明，星系和星系团的质量中存在着占比相当大的不发出电磁辐射的暗物质。

暗物质就按其本质来分类是分为两大类：重子暗物质和非重子暗物质。重子参与电磁作用，其本身是能够发出电磁辐射的，但由于条件因素的缺乏，未能发出电磁辐射从而不被人类所探测到，因而成为了重子暗物质。例子有不发光的行星、死亡了的恒星如温度极低的白矮星、黑矮星，以及没有引起核聚变的暗弱褐矮星等。实际上，WMAP的观测结果表明。重子暗物质占比在整个宇宙的暗物质中是很少的，整个宇宙的暗物质的主要成分或者说是绝大部分都是非重子暗物质。非重子暗物质不发光的原因是它不参与电磁作用，它们被称为WIMPs（Weakly Interacting Massive Particles），即有质量弱作用粒子。这种粒子之间，以及这种粒子于其他种类的粒子之间，只有引力作用和弱相互作用。截至目前人类依然没有找出这些有质量弱作用粒子到底是什么粒子，寻找该种粒子的过程仅是停留在通过猜测给出候选者（表2.1）的阶段。

表2.1 一些可能的非重子暗物质粒子候选者