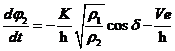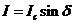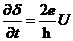基于约瑟夫森结的相位量子比特的理论模拟毕业论文
2020-02-18 10:32:03
摘 要
未来发展计算机芯片,我们必将涉及到量子领域,若我们能够合理利用量子系统,反而能够使量子计算机成指数倍的提高计算效率。本文主要介绍了量子计算机的核心量子比特的其中一种超导相位量子比特。首先简单介绍了量子计算机相对于经典计算机有着很大的发展空间,然后扩展了宏观量子信息、退相干性和约瑟夫森结等知识。
宏观量子现象,即是在宏观上能够观测到的量子效应,只有我们能够观测的量子效应我们才能够设计为量子比特。约瑟夫森结就是现在一种很好的观测宏观量子现象的载体。约瑟夫森结组成就是两超导体由很薄的绝缘层隔开,我们就能够通过库伯对隧穿绝缘层的效应来观测宏观量子效应。最后利用约瑟夫森结设计了一个超导相位量子比特电路,并通过量子力学方面的计算来讲解系统,将系统看作小球在势垒中的运动,给出了能级图,直观解释库伯对隧穿变化的原因,之后还讲解了如何操控和观测量子比特,在电路中,我们只需要改变偏置电流再测量结端电压就能够测出量子比特中存储的信息是0还是1。
关键词:量子计算机;宏观量子现象;约瑟夫森结;超导量子比特
Abstract
In the future, the development of computer chips will inevitably involve the quantum field. If we can make rational use of the quantum system, we can make the quantum computer exponentially improve the computational efficiency. In this paper, we mainly introduce one of the core quantum bits of quantum computer, superconducting phase quantum bits. Firstly, it briefly introduces that quantum computer has a great development space compared with classical computer, and then expands the knowledge of macroscopic quantum information, decoherence and Josephson junction.
Macroscopic quantum phenomena are quantum effects that can be observed macroscopically. Only the quantum effects that we can observe can we design quantum bits. Josephson junction is a good carrier for observing macroscopic quantum phenomena. The Josephson junction consists of two superconductors separated by very thin insulating layers. We can observe the macroscopic quantum effects through Cooper's effect on tunneling insulating layers. Finally, a superconducting phase quantum bit circuit is designed using Josephson junction, and the system is explained by the calculation of quantum mechanics. The system is regarded as the movement of a small ball in the barrier. The energy level diagram is given to explain the reason why Cooper tunnels change intuitively. Then, how to manipulate and observe the quantum bit is explained. In the circuit, we only need to change the bias current to measure again. Measuring the terminal voltage can determine whether the information stored in the qubit is 0 or 1.
Key words:Quantum computers; macroscopic quantum phenomena; Josephson junctions; superconducting quantum bits
目 录
摘 要 I
Abstract II
第1章 绪论 1
1.1 量子计算机 1
1.2 宏观量子现象 1
1.3 退相干性 2
1.4 量子比特的发展现状 2
1.5 本文的主要内容 3
第2章 约瑟夫森效应 4
2.1 约瑟夫森结 4
2.2 约瑟夫森效应 4
2.3 小结 6
第3章 超导量子比特 7
3.1 超导电荷量子比特 7
3.2 超导磁通量子比特 8
3.3 超导相位量子比特 8
3.4 混合性超导量子比特 10
3.5 小结 10
第4章 超导相位量子比特电路 11
4.1 电路结构 11
4.2 能级结构 12
4.3 操控测量方法 14
4.4 量子比特耦合 15
4.5 小结 16
第5章 结论 17
参考文献 19
致谢 21
第1章 绪论
1.1 量子计算机
上个世纪60年代人们就提出过著名的摩尔定律,即电子芯片的集成度在每一年到两年内会翻一番。在后来的几十年中芯片的发展基本都印证了这个定律,但是我们不难想到摩尔定律终究会被终结。因为在当前经典计算机的背景下,随着芯片集成度的提高,一般都要伴随着晶体管的尺度越来越小,且不说能不能保持减小尺度的制作,当尺度减小到一定的量级时,就会出现量子效应,这样曾经的以经典物理理论为基础的经典比特就会出现问题,为了能够继续提高芯片的集成度,人们需要寻找新的方向。直到宏观量子效应的提出和实现,人们终于找到出路,既然量子效应避无可避,何不直接加以利用,借助宏观量子现象,人们提出了量子计算机的概念[4]。
最初,人们为了观测量子现象而研究宏观量子效应。直到1982年美国物理学家费曼提出了量子计算的概念,于是20世纪80年代发展出了量子计算和量子信息这些交叉学科大大拓展了宏观量子效应的前景。我们现在所用的计算机的存储系统像光盘、磁盘等等,都是利用一些经典物理现象来定义比特0和1(比如高电位为1低点电位为0等).同时我们也知道在量子力学中,我们一般把某个时间的态写为
| (1.1) |
其中的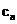 就可以用来代表我们所需要存储的信息(一般来说2态系统更加适合作为量子比特,类似经典比特只有0和1两态),光是一个量子比特相比与只有2个信息的经典比特就能存n个信息,若我们还有另一个相同的量子比特,他们一起的系统的状态就可以写为
就可以用来代表我们所需要存储的信息(一般来说2态系统更加适合作为量子比特,类似经典比特只有0和1两态),光是一个量子比特相比与只有2个信息的经典比特就能存n个信息,若我们还有另一个相同的量子比特,他们一起的系统的状态就可以写为
| (1.2) |
这样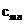 的数量直接就扩大到了
的数量直接就扩大到了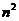 个,依次类推,量子比特的信息存储量和量子比特数量成指数倍增长,对于k个量子比特我们就能够得到
个,依次类推,量子比特的信息存储量和量子比特数量成指数倍增长,对于k个量子比特我们就能够得到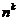 个存储信息,而且提高信息存储量之后,我们也可以通过设计算法来提高计算机的计算速度,所以相比经典计算机,量子计算机能够实现飞跃式的进步。
个存储信息,而且提高信息存储量之后,我们也可以通过设计算法来提高计算机的计算速度,所以相比经典计算机,量子计算机能够实现飞跃式的进步。
1.2 宏观量子现象
宏观量子现象,顾名思义就是在宏观上能够观测到的量子效应,例如我们耳熟能详的薛定谔的猫假设就是较早时期,薛定谔想通过宏观现象观测量子效应的一种假想实验。现阶段在低温环境下,已经发现了多种宏观量子现象,比如液态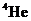 在饱和蒸汽压下温度降到2.172K时发生超流相变,或者超导体的温度低于临界温度时发生的波色-爱因斯坦凝聚现象。而我们所要涉及的约瑟夫森效应也与超导体的宏观量子现象有着直接的关系,虽然说超导中的库伯对本身就是一种宏观量子效应,但是电子在超导体中的自由度太高,并不能代表宏观量子现象的变化。
在饱和蒸汽压下温度降到2.172K时发生超流相变,或者超导体的温度低于临界温度时发生的波色-爱因斯坦凝聚现象。而我们所要涉及的约瑟夫森效应也与超导体的宏观量子现象有着直接的关系,虽然说超导中的库伯对本身就是一种宏观量子效应,但是电子在超导体中的自由度太高,并不能代表宏观量子现象的变化。
想要观测宏观量子现象就需要一个独立的宏观变量,例如超导体中的相位和电荷数,超导体中的电子在费米球附近形成库伯对并且凝聚到一个能量基态上。这种能量基态可以用一个宏观波函数来表示
| (1.3) |
其中n和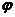 即可以分别表示超导体的电荷数和相位,在下面会具体介绍这两种变量。其中约瑟夫森结就是这样一个能够测量超导体的相位或电子数的工具。
即可以分别表示超导体的电荷数和相位,在下面会具体介绍这两种变量。其中约瑟夫森结就是这样一个能够测量超导体的相位或电子数的工具。
1.3 退相干性
众所周知,在开放的量子系统中的量子相干性会因为与环境发生量子纠缠而随着时间逐渐消失,这种效应即为量子退相干。对于量子计算机来说,量子信息的处理过程主要就是通过量子态的相干叠加来完成的,通常来说,量子比特要保持较长时间的相干性是非常困难的,通常我们需要在短时间之内完成观测,之后便会逐渐发生退相干。所以在设计量子比特时,我们需要足够的相干时间[9]。
目前实验上较好的量子比特的相干时间大约为10微秒,我们只能够进行两量子位逻辑门的计算。如果要超越现在的电子计算机的水平,量子计算机估计需要一千多个量子比特所构成,当然以现在的水平来说还相差非常远。因此消减退相干是量子计算中非常重要的一环。
现在一般对抗退相干的方法主要有两个思路:一是通过优化超导电路的物理结构使其最大程度的阻隔环境带来的影响。二是通过超导量子比特之间的可控耦合灵活的设计量子计算的编码,从而降低量子逻辑门的运输时间,从而间接地对抗退相干。
1.4 量子比特的发展现状
早在几十年前人们就已经提出了量子比特的理论设想,只是苦于实验条件的限制一直存在与理论和预言中。20世纪80年代时期,诺贝尔物理学奖获得者莱格特第一次提出的可以利用超导约瑟夫森结来观测宏观量子现象。随着实验和样品加工技术的发展,人们也逐渐观测到了能级量子化和量子隧穿等宏观量子现象,成功验证了莱格特的想法也为量级计算机带来了一段研究热潮。
目前主要的量子比特设计方法有核磁共振、光腔、离子阱、量子点、超导材料等,其中理论上暂时只有量子点和超导体等固态材料才能够实现集成,是未来更好的选择和发展方向,也是如今研究的主流方向。不过至今量子计算机的研究仍然还处在实验室阶段,这其中主要的原因即是刚刚所提到的相干性的问题,量子系统较为脆弱,周围的环境很容易会影响到量子相干性,导致我们能够操控、观测并使用的比特非常少。
现在在量子方面一般只能做到2到3个量子比特,超导量子比特则能够实现10个左右的量子计算,加拿大的D-Wave公司和谷歌公司曾经合作制作了一台利用量子退火效应计算的16比特量子计算机[4]。由于苛刻的实验条件,国内对超导量子计算机的研究距欧美国家还有一定差距,一般研究则集中在理论方面。
1.5 本文的主要内容
本文主要是介绍了量子计算机的基本概念,然后简单介绍了约瑟夫森效应和利用约瑟夫森结所制作的三种超导量子比特的基本原理,并利用约瑟夫森结来设计一个超导相位量子比特电路,给出观测和控制的方法然后耦合了两个相位量子比特。
第2章,介绍了约瑟夫森结的构成和两种约瑟夫森效应的原理和对应的现象,通过费米方程计算出约瑟夫森第一方程和第二方程,再通过两个方程推导了直流和交流约瑟夫森效应。
第3章,介绍了三种利用约瑟夫森结的超导量子比特以及其各自的优缺点和混合超导量子比特,其中超导电子比特利用电荷数来定义,超导磁通量子比特和超导相位量子比特则由相位来定义。
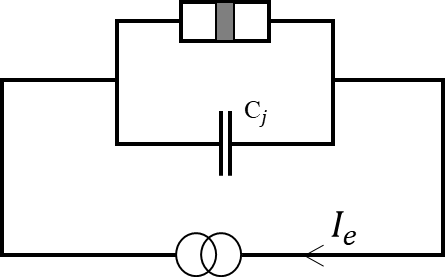
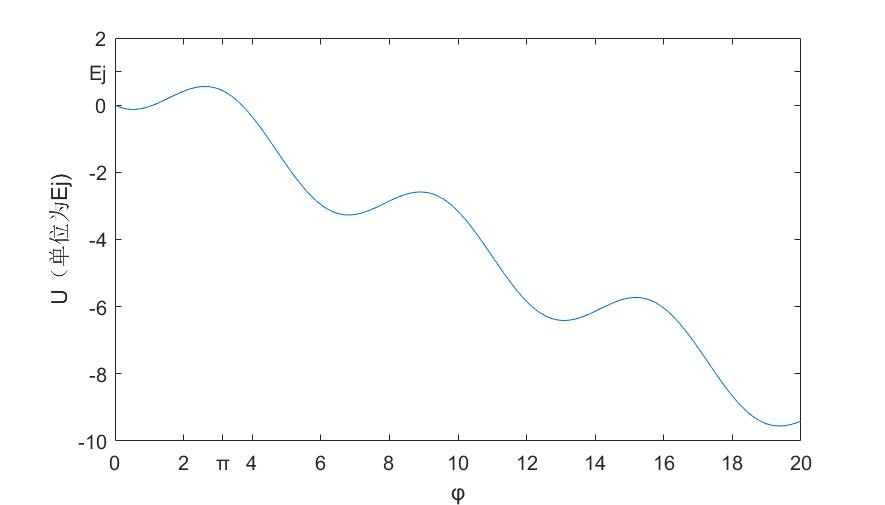
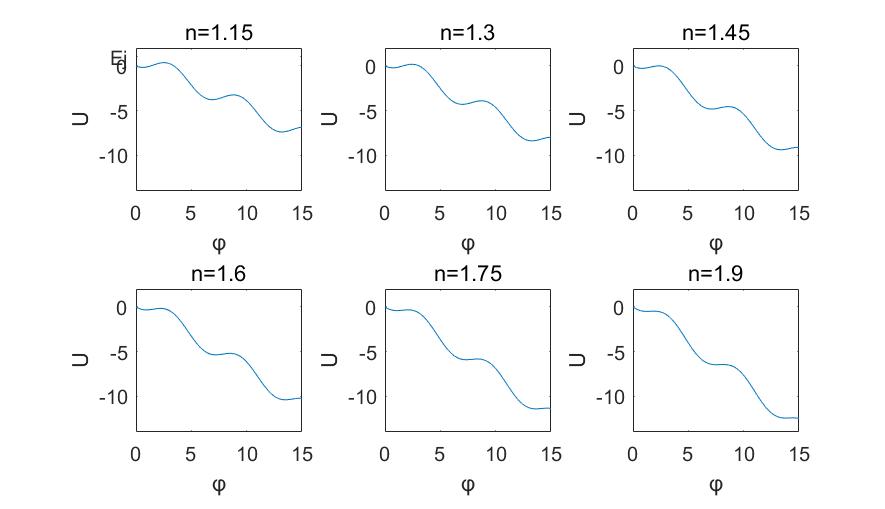
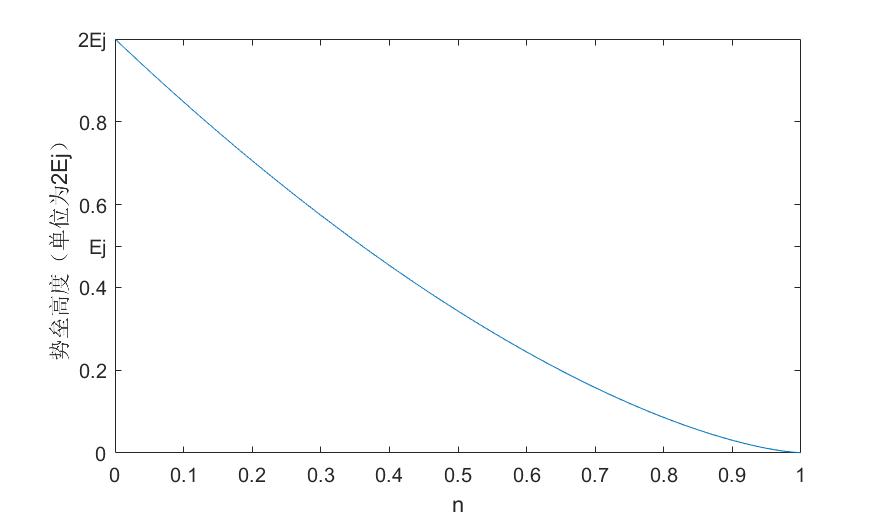
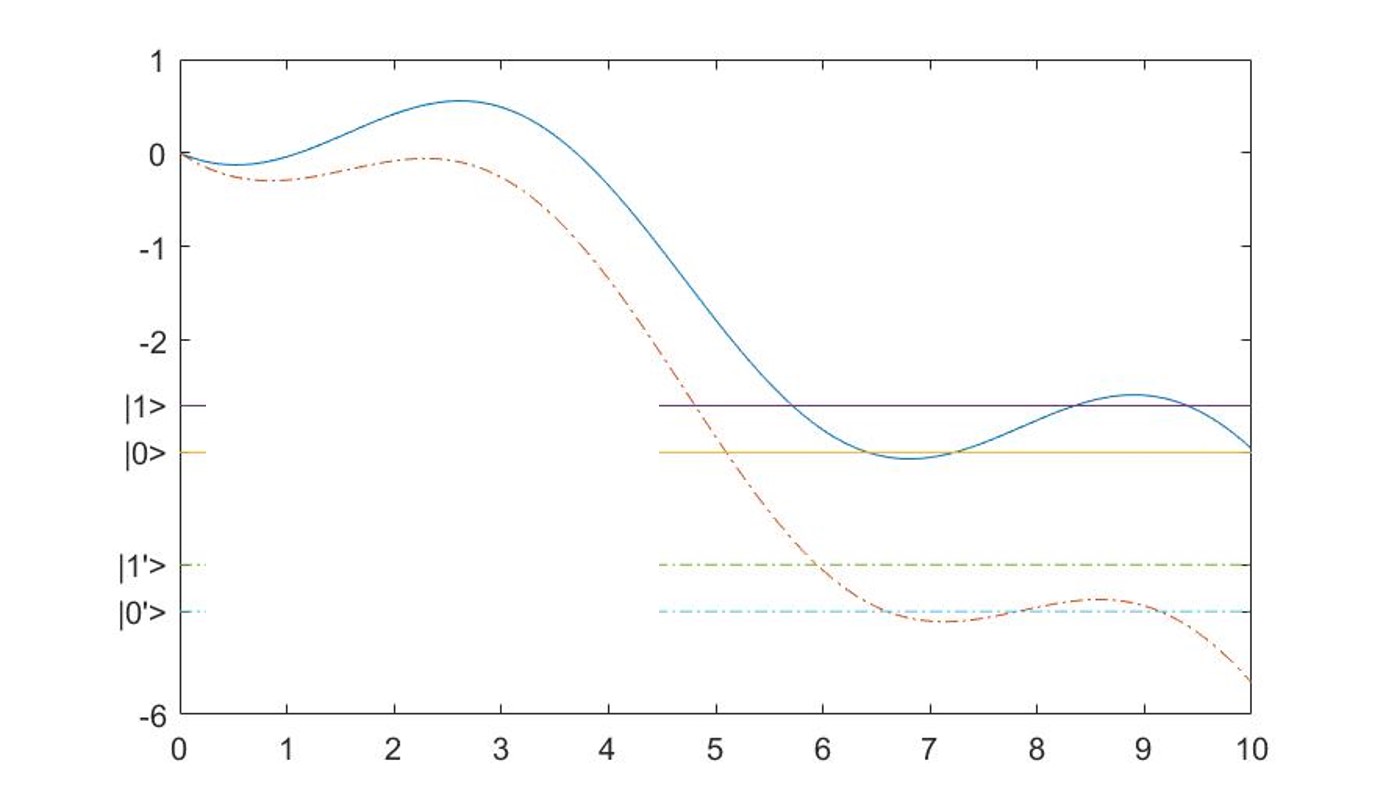
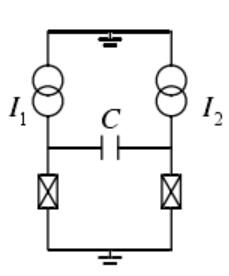
第4章,利用约瑟夫森结设计了一个超导相位量子比特电路,通过哈密顿量给出小球模型的势能形式并画出曲线图和不同偏置电流下势能曲线的变化图,利用微波辐射控制信息、约瑟夫森结两边电位来观测信息,利用电容耦合两个相位量子比特。
第5章,总结研究过程和不足,对未来的发展方向和可改进的地方提出意见。
第2章 约瑟夫森效应
2.1 约瑟夫森结
简单来说约瑟夫森结就是SIS隧道结,即两边为超导体,中间用非常薄的绝缘介质连接,当绝缘层薄到10埃左右,隧道结就会出现库伯对的隧穿现象,即库伯对穿过绝缘势垒后仍然保留着配对的状态,从而形成超电流,大小能够通过约瑟夫森方程给出。这时在宏观上的表现为电流无阻通过中间的绝缘层,即SIS结两端并没有电压降。不过这种结一般只能够承受几十微安到几十毫安的电流,超过的话则会出现电压降而失去超电流现象,我们将该电流大小称之为临界电流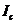 。
。
其实,当结区两端出现电压时,除了单电子隧穿效应之外,还会出现交变超导电流,于是会产生从结区向外辐射的电磁波,该电磁波在微波的波段范围。这种特性也称之为交流约瑟夫森效应,在下面 约瑟夫森效应中有更详细的介绍,虽说叫做交流约瑟夫森效应,约瑟夫森结两端所加的仍是直流电,当有电压存在时,结两端的超导题相对的就有电位差,即这两对超导体的凝聚态不再处于同一能量水平上。所以为了满足能量守恒,在电子对隧穿进入结的另一侧则伴随着能量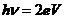 的光子辐射出去。
的光子辐射出去。
约瑟夫森结有着广泛的应用:利用约瑟夫森结组成的超导环制作的超导量子干涉仪,在下面的超导磁通量子比特中有涉及到,是一种非常敏感的磁强计。它能偶测出非常微弱的磁场像人体中的心脏磁场、肺部磁场、大脑神经磁场等,为医学事业也能提供突出的贡献;约瑟夫森效应能够提供一种具有完全再现性的频率和电压转换,我们可以将该频率定义标准值来进行精确的计算,即约瑟夫森电压标准;当然,就像本文主要介绍的,约瑟夫森结还能够用于设计超导量子比特。
想要制备约瑟夫森结这样精细的结构也非常困难,像比较典型的“夹层”型约瑟夫森结,其制作的方法一般是在一块干净的玻璃板上铺一层厚度大约几百纳米的超导金属薄膜,形成薄膜后再利用氧化方法使金属薄膜表面形成绝缘的氧化膜,之后再镀另一层超导金属膜。过程看似简单,但是由于绝缘层的厚度需要只有几纳米量级只有几个原子的厚度,在制作时候,氧化层容易产生漏洞从而达不到绝缘的效果。而且我们经常希望绝缘层的厚度变化要尽可能的小,所以想要制作一个特定参数的约瑟夫森结可以说非常困难[5]。
2.2 约瑟夫森效应
之前说过,在约瑟夫森结中,只要绝缘层的厚度薄到几纳米的量级,就会发生库伯对隧穿的现象,这就是约瑟夫森效应。1962年约瑟夫森从理论上预言了隧道效应后[23],两年后他就进一步给出了描述这种库伯对隧穿的基本方程[24],即约瑟夫森第一和第二方程。下面简单推导一下两个方程。
通过第一章的公式(1.3)我们可以得到两边的超导体(分别用n为1和2表示)的宏观波函数分别为
| (2.1) |
其中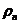 表示对应超导体中的库伯对密度。因为两边库伯对能够隧穿发生耦合,则
表示对应超导体中的库伯对密度。因为两边库伯对能够隧穿发生耦合,则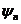 满足耦合的薛定谔方程
满足耦合的薛定谔方程
| (2.2) |
其中K表示耦合强度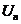 表示库伯对的能量。若结两端存在电压V并取绝缘层为零势能点,则
表示库伯对的能量。若结两端存在电压V并取绝缘层为零势能点,则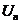 可表示为
可表示为
| (2.3) |
将能量(2.3)和波函数(2.1)带入薛定谔方程(2.2)并计算可以分别得到,实部相等
| (2.4) |
和虚部相等
| (2.5) |
从(2.4)我们可以看到两边库伯对密度随时间变化率为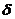 的正弦函数且两边变化率互为相反数,代表库伯对互相隧穿,而超导电流密度正比于库伯对时间变化率
的正弦函数且两边变化率互为相反数,代表库伯对互相隧穿,而超导电流密度正比于库伯对时间变化率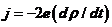 ,于是得到电流与相位
,于是得到电流与相位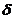 的关系即为约瑟夫森第一方程为
的关系即为约瑟夫森第一方程为
| (2.6) |
其中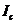 为约瑟夫森临界电流
为约瑟夫森临界电流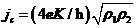 ,
,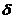 为约瑟夫森结绝缘层两边的超导波函数的相位差。
为约瑟夫森结绝缘层两边的超导波函数的相位差。
如果约瑟夫森结两边是同种超导体,即上面的方程中都满足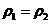 ,于是(2.5)两式可以互相消除得到约瑟夫森第二方程
,于是(2.5)两式可以互相消除得到约瑟夫森第二方程
| (2.7) |
其中2e表示载流子是由两电子组成的库珀对,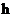 为约化普朗克常数,U为约瑟夫森结两端的电压。
为约化普朗克常数,U为约瑟夫森结两端的电压。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:
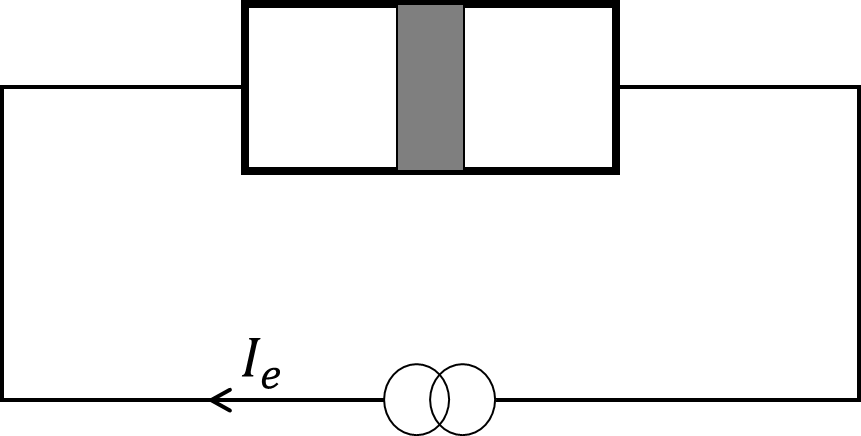

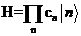
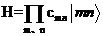
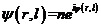
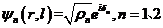
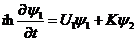 ,
,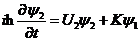
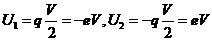
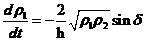 ,
,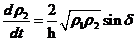
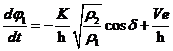 ,
,