基于MATLAB的模拟退火算法实现及其工程应用毕业论文
2020-02-18 10:38:19
摘 要
本文借助了科学计算语言MATLAB来实现模拟退火算法,首先通过编制算法程序解决了经典多项式非确定性难题——旅行商问题,试验得到的最终优化路线与理论最佳结果相比,差距较小;接着利用模拟退火算法对船舶航速问题进行优化处理,以降低整个航程的主机燃油消耗量为最终目标,将整个航程分段处理,在MATLAB上求得各分段航程的最佳航速,试验优化后的主机燃油量降低了3.0%,节油效果明显,为船舶公司的节能提供了理论基础和实现思路。
论文主要研究了模拟退火算法以及利用MATLAB软件实现该算法的过程。
研究结果表明:基于MATLAB的模拟退火算法能够比较快速准确的找到全局最优解,较传统的算法更迅速、准确、实用性更广。
关键词:模拟退火算法、Metropolis准则、MATLAB、旅行商问题、分段航速优化
Abstract
In this paper, the scientific computing language MATLAB is used to realize the simulated annealing algorithm. Firstly, the classical polynomial nondeterministic problem -- traveling salesman problem is solved by programming algorithm. Then the simulated annealing algorithm optimization problem of ship speed, in order to reduce the fuel consumption of the entire voyage host as the ultimate goal, the whole voyage segmentation processing, on the MATLAB each section for the best speed of the voyage, test host fuel quantity was reduced by 3.0% after optimization, oil-saving effect is obvious, for the shipping company provides the theoretical basis and implementation approach for energy conservation.
This paper mainly studies the simulated annealing algorithm and the process of realizing the algorithm with MATLAB software.
The results show that the simulated annealing algorithm based on MATLAB can find the global optimal solution quickly and accurately, which is faster, more accurate and more practical than the traditional algorithm.
Key Words: simulated annealing algorithm, Metropolis criterion, MATLAB, traveling salesman problem, section speed optimization
目录
第1章 绪论 1
1.1 选题背景及研究意义 1
1.2 国内外研究现状 2
1.3 本文研究内容 3
第2章 模拟退火算法 4
2.1 模拟退火算法介绍 4
2.2.1 模拟退火算法 4
2.2.2 Metropolis准则 5
2.2 模拟退火算法的基本思想 6
第3章 基于MATLAB的模拟退火算法实现 7
3.1 旅行商问题概述 7
3.2 基于MATLAB的模拟退火算法实现 7
3.3 旅行商实例 8
第4章 分段航速优化 10
4.1 船舶航速优化的背景 10
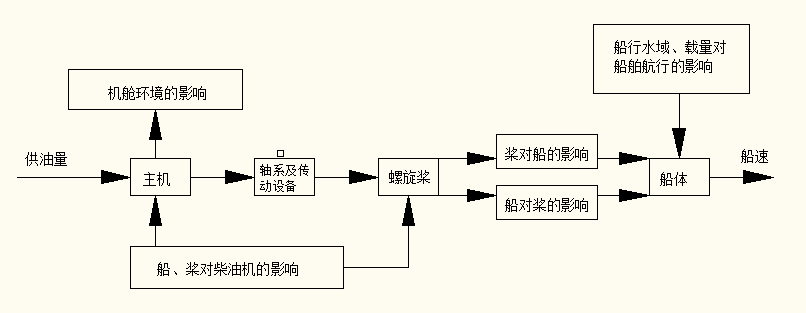
4.2 船机桨能量传递关系 10
4.3 试验船舶参数 11
4.4 船舶阻力 12
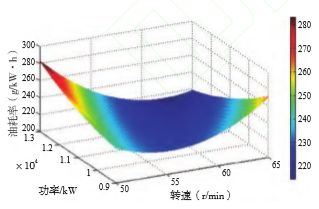
4.4主机燃油消耗率数据库 13
4.5 船舶主机油耗量模型 14
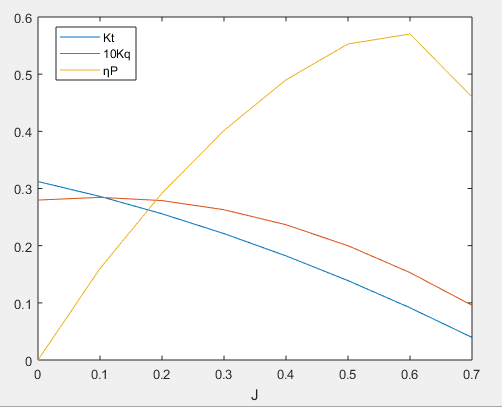
4.5.1螺旋桨淌水特性 14
4.5.2 船速与主机转速模型 15
4.5.3 航程油耗计算 15
4.6 分段航速优化模型的建立 16
4.6.1 优化航速介绍 16
4.6.2 分段优化航速模型 17
4.7 船舶航速优化试验 17
第5章 结论与展望 19
5.1 结论 19
5.2 展望 19
参考文献 20
致谢 22
第1章 绪论
1.1 选题背景及研究意义
随着社会的发展,人们对工程优化问题的解决提出了全新的和更高的要求,例如系统控制更加精准、生产调度问题上一步到位、模式识别更加迅速等。在这种大环境下,传统的优化技术明显不能满足我们的生产需求,所以人们迫切地需要全新的计算方法和高效的优化技术。在这种背景下,各种智能优化算法随之诞生[1]。
从上世纪末开始,人们通过模仿大自然种种现象的过程,分析其背后的原理,据此提出了大量先进的优化算法。其中就包括模拟人体免疫系统的信息处理机制,提出了人工免疫算法;模拟生物遗传的规律,提出了遗传算法;模拟蚁群的觅食行为,提出了蚁群算法;模拟物体退火的过程,提出了模拟退火算法等。由于这些先进算法具有模拟智能的特点,在此统称为智能优化算法。和传统的优化算法相比,智能优化算法原理都非常简单易懂,实现起来也很方便迅速;此外,这些算法在复杂的优化问题上表现优异,无论是其算法的收敛性还是搜索速度,都是大大优于传统优化算法。正是因为这两点,智能优化算法在工程优化问题上得到迅速推广和应用,引来越来越多的人投身于对此的研究热潮[2]。
模拟退火算法作为智能优化算法之中的一员,在当今VLSI设计、图像识别处理、生产调度等方面扮演着越来越重要的角色。由于其计算过程简单,方便学习理解;适用性广,可应用于各类优化问题上的优点,本文选取其作为研究对象,从算法本身理论出发,对其原理和基本思想进行了系统阐述和深入的分析,方便读者全方面深入地了解模拟退火算法。
MATLAB 作为一种计算机科学语言,由于其对数值分析快速精准、矩阵计算方便、数据可视、建模简单等优点,为科学工程领域的计算分析提供了强大有力的支持。在模拟退火算法的实现过程中,MATLAB其强大的矩阵处理能力、优秀的绘图功能以及迅速的数值分析处理计算能力都给我们模拟退火算法的实现提供了巨大的帮助和支持[3]。
本文对基于MATLAB软件实现模拟退火算法的方法进行了介绍,并以经典的旅行商问题作为案例进行讲解,能够让读者对模拟退火算法有了初步的认识;其次将该方法应用于航速优化问题上,表明了算法在现实工程案例问题上优秀的处理能力。在将来遇到类似工程案例需要寻找最优解的问题上,我们就可以考虑运用模拟退火算法来解决问题,具有很强的实际性。
1.2 国内外研究现状
早在上世纪八九十年代,Dolan等人[4]、Hong-ming等人[5]、Floquet等人[6]和Cardoso等人[7]对于模拟退火算法在化工过程的用途上进行了摸索,并成功将算法应用到化工过程的稳态设计与合成。2005年,Richard Faber,Tobias Jockenhövel和George Tsatsaronis将算法用于对能源化工过程的动态优化,选择MATLAB作为DAE求解器,在SA算法中,DAE求解器总是收敛的,减少了DAE求解时间。而在具体实例的分析中,发现并行变分法能有效提高动态优化问题的模拟退火收敛性,和以前的顺序方法相比有着更低的迭代量进而减少了计算时间[8]。2014年,Hajar Bagheri Tolabi和Shahrin Md. Ayob用MATLAB软件实现了一种基于模拟退火算法的元启发式方法,可以检测全局太阳辐射的数值,研究成功后,用来估算伊朗6个不同气候城市水平表面月平均日太阳辐射,在城市的气候研究上发挥了作用[9]。同年,Changxing Zhang等人提出了一种基于CSM的的不稳定热响应试验的历史无关算法,为了缓解不适应问题,在MATLAB中进行反演计算,得到参数估计的上下界,提高了参数估计的可靠性,拥有了比一般的叠加算法更快的计算速度和更精确的计算结果。在热率不稳定的现场,热响应测试估算地面导热系数的体积热容与实测吻合较好,较传统算法,减少了成本和时间[10]。
与此同时,国内也愈来愈重视对模拟退火算法的研究。徐雷于1989年成功将模拟退火算法运用于模式识别中来,效果显著[11]。胡山鹰等人在1997年更进一步地完成了对有约束问题的探讨,在原有的无约束非线性规划问题上,形成了完整的对非线性规划问题全局优化的解决办法[12]。1999年,王子才等人提供了一种基于混沌变量的混沌模拟退火优化算法,改进后的算法极大地提高了全局优化问题的求解效率[13]。传统方法获得良好的PID参数是相当困难的,为此任妮等人利用模拟退火算法来对PID参数进行优化,以MATLAB作为仿真工具,在超调量和传统方法相同的情况下,模拟退火方法所需的调节时间明显得到减少,适用于并行处理[14]。至此,虽然国内对模拟退火算法的研究历史较短,但是在科研前辈们的辛苦专研下,模拟退火算法开始慢慢发展并且逐渐地应用于国内生产生活的方方面面。
近年来,我们不再满足单一模拟退火算法给我们带来的便利,而是更多地将眼光放在了多种智能优化算法相结合的层面。在2015年,Mohammad Shokouhifar等人把遗传算法和模拟退火算法相结合,提出了一种基于演化的多目标判据来简化含MOSFET的模拟电路的符号分析,和传统的简化准相比控制了最终的简化错误率[15]。国内,苏镜吾根据遗传算法易过早收敛的缺点和模拟退火算法保留不符合适应度要求解的缺点,将两者智能算法结合起来,发挥各自算法的优势,更有效的实现了对PID参数的优化[16]。汤伟等人为了获得较单一智能优化算法更为理想的对PID参数的控制效果,将模拟退火算法和粒子群优化算法相结合,提出了一种模拟退火粒子群混合算法,最后试验结果表明,对PID的控制效果更优异,更好地满足了现实生活的需求[17]。从近年来模拟退火算法的发展趋势中,我们不难看出,单一的智能优化算法又再一次达不到我们全新的要求,在未来我们的研究方向会更偏向于混合优化算法上,通过发挥各自算法的优势,避免算法本身的局限性,更优地更全面地解决实际工程案例问题。这无疑是智能优化算法的一种全新进展,希望有兴趣的读者能够投身于这份伟大的事业中来。
1.3 本文研究内容
本文从学习模拟退火算法出发,对算法研究透彻后;学习掌握MATLAB软件的用法,并用其成功解决模拟退火算法经典案例——旅行商问题;在此基础上将算法应用于对船舶航速的优化,以获得目标船舶更低的主机燃油消耗量,以此说明算法的可行性和有效性。本文各章节具体研究内容如下:
第1章:阐述了当前工程优化问题的大环境和本文研究的内容——模拟退火算法及其在MATLAB上的实现,并结合国内外的研究现状分析,说明了模拟退火算法在当今社会乃至未来都将起到举足轻重的作用,以此表明研究模拟退火算法的必要性。
第2章:详细全面的介绍了模拟退火算法的主要内容、实现路线以及算法所涉及到及其重要的Metropolis准则,为下文解决经典案例提供了理论基础和思路。
第3章:从旅行商问题eil51案例本身出发,比较详细地讲解了算法每一步在MATLAB上是怎么具体实现的,最后成功地在软件上实现算法,最终结果与标准结果对比后分析不足之处。
第4章:选取30万吨级的VLOC船舶作为本文研究的对象。根据《民用船舶动力装置原理与设计》一书中提及的船机桨匹配关系作为基本理论[18],获得了船机桨各功率之间传递关系图;通过目标船历史数据分析,建立了主机燃油消耗率数据库;以整航程主机燃油消耗量最低作为寻优目标,将航程根据工况不同分段处理,通过改变分段航程的船舶航速,以获得最低的燃油消耗量,从而达到船舶节油的目的。
第5章:总结对模拟退火算法的学习研究以及本文试验结果的分析,以此指出自身不足之处和对未来的展望。
第2章 模拟退火算法
2.1 模拟退火算法介绍
2.2.1 模拟退火算法
退火,在自然界,是指一种物体逐渐降温的物理现象。温度越低,代表着物体的能量也越低;温度达到最低的话,物体也就达到了能量最低的状态。这无疑跟我们所要寻找工程问题最小解(造价最低、耗能最少、路线最短等)的目的不谋而合。对此,模拟退火成为我们解决优化问题的一种方向。
模拟退火,顾名思义,就是模拟物体逐渐降温的过程。在具体寻优问题上,我们可以发现模拟退火和物理退火的众多相似性,如表2.1所示。
表2.1 物理退火和模拟退火的比较
物理退火 | 模拟退火 | 物理退火 | 模拟退火 |
粒子状态 | 解 | 能量 | 目标函数 |
能量最低态 | 最优解 | 冷却 | 控制参数的降低 |
熔解过程 | 设定初温 | 等温过程 | Metropolis抽样过程 |
模拟退火算法就是将自然界物理退火现象中的过程和前后状态应用于我们解决问题的过程。退火前要先加热,固体内部粒子剧烈运动,这时粒子状态是无序的,就类似实际问题的最初各种解决办法;慢慢降温过程中,粒子趋于稳定,就好比我们筛检解的过程;到最终粒子相对静止后,我们也就获得了最优化的解。简而言之,模拟退火算法是一种受到大自然启发而出现的先进优化算法,它可以在大范围内求得问题最优化的解。
我们将实际寻优问题简化为一个毫无规律的函数(如图2.1所示),而我们所要求得的就是函数最小值作为我们的最优解。某一时刻我们获得了A点的解,我们模拟退火求解的话,就好像在A点所在凹形内慢慢下降,在温度达到最低时,我们也求得了凹形的最低点C,这时我们的求解过程就结束了(因为无论朝哪个方向努力,结果只会越来越大),最终我们只能找到一个局部最优解C。但是从全局看C显然不是我们的最优解,在实际问题更加复杂的情况下,我们如果只找到初始解所在的凹型最优解的话,显然是不符合我们提出模拟退火算法的最初目的的。这时我们就需要用到模拟退火算法的核心思想——Metropolis准则。
2.2.2 Metropolis准则
Metropolis准则最早在1953年由美国物理学家 N.Metropolis 和同仁发表《Equation of state Calculations by Fast Computing Machines》文章中所提及,它是一种以一定概率接受劣于原有解(即恶化解)的准则[19]。开始状态为i,在温度为T时,产生新状态j,若Ejlt;Ei,则将j设为新的状态;否则,若概率 p=exp[-(Ej-Ei)/kT]大于[0,1)区间的随机数,则仍将j设为新状态;若不成立,则将i设为新状态。Metropolis准则的数学表达式为:
(2-1)
基于Metropolis准则的模拟退火算法优化过程,可以避免搜索求解过程中陷入局部极小,并最终趋于问题的全局最优解。接着上面的模拟寻优函数(图2.1)来说明,到C点后,在温度没有达到最低时,我们还可以继续得到解D(恶化解),此时Dgt;C,由Metropolis准则的可确定新解D是否被接受,当我们接受D作为我们新的解后,再继续求解过程中我们还可能依次接受新解B、E、F,到最后,我们就可能“爬过”CG之间的“大山”,得到图上最优解G。
 由式(2-1)可知,接受概率P与温度T有关系,温度越高,接受概率P也就越高,当温度趋于0时,接受概率P近似于0。在算法刚开始运行时,我们可以接受恶化解概率高,意味着我们可以搜索目标解的范围也就越大,与我们大范围求解的前提一致;算法运行快结束时,我们基本不能接受恶化解了,直到算法结束,我们也就获得了最优解。
由式(2-1)可知,接受概率P与温度T有关系,温度越高,接受概率P也就越高,当温度趋于0时,接受概率P近似于0。在算法刚开始运行时,我们可以接受恶化解概率高,意味着我们可以搜索目标解的范围也就越大,与我们大范围求解的前提一致;算法运行快结束时,我们基本不能接受恶化解了,直到算法结束,我们也就获得了最优解。
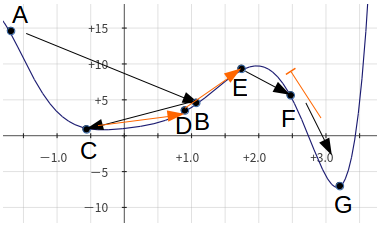
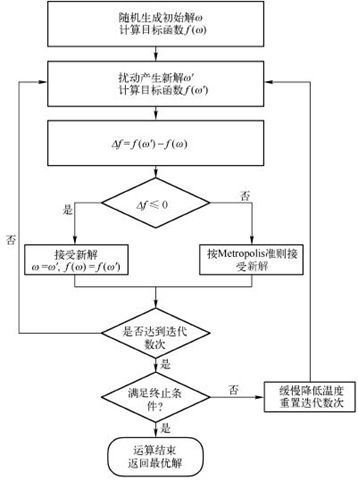
图2.2 模拟退火算法流程图
图2.1 Metropolis准则示意图
2.2 模拟退火算法的基本思想
- 初始化:足够大的初始温度(一般大于1000℃),足够小的终止温度(一般小于0.1℃),初始温度时对应问题的初始参数,温度递减函数q(qlt;1),每一个温度时的迭代循环次数即Metropolis链长L;
- 外循环:每一次循环对应着相同的T值,T值按照递减函数慢慢减少,循环次数根据初末温度以及递减规律得出;
- 内循环:内循环次数为L;
- 通过扰动产生新的参数;
- 计算,其中为参数的评价函数;
- 若 lt;0,则接受成为新解,否则以概率exp(- /kT)gt;rand接受成为新解,其中rand为(0~1)的随机数,k为固定值,据情况而定,除上述以外情况,仍保留作为下一次循环的旧参数;
- 重复步骤(4~6)L次,选出最后结果作为当前温度下的最优解;
- 温度按递减函数减少一次,此时的为步骤7产生的解,为此时对应的参数;
- 重复步骤(3~8),直到最终温度小于步骤1设定的终止温度;
- 最终解为最后一次外循环步骤7产生的解。
上述模拟退火算法的基本思想可用流程图(如图2.2所示)表示。
第3章 基于MATLAB的模拟退火算法实现
3.1 旅行商问题概述
旅行商问题(TSP)是一种非确定性多项式难题,长期以来一直是一种基于线性规划和非线性规划的离散或组合优化技术领域的一个有趣问题。它具体的概述是:给定n个城市相互之间的距离,某一旅行商从某个城市出发,要求抵达每个城市一次且仅一次,最后回到出发城市,怎样安排路线才使其所走路程最短。换成数学模型来说,就是寻找n 1个数据的最小值,数据来源是城市之间的距离,其中n 1个数据不重复代表两个城市之间的距离,其数学表达式为:
(3-1)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
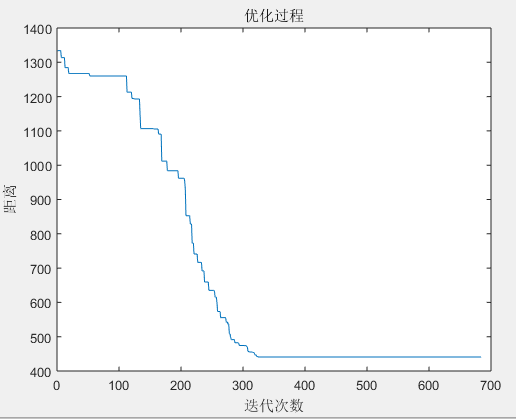
相关图片展示:
![C:\Users\Administrator\AppData\Roaming\Tencent\Users\2264530805\TIM\WinTemp\RichOle\J8N4TR)4C{]O%V19PB][$}G.png](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw4299_2020218103816335.png)
![C:\Users\Administrator\AppData\Roaming\Tencent\Users\2264530805\TIM\WinTemp\RichOle\$Y`~5]XDSR$SIAA)HL[XP`B.png](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw4299_2020218103816346.png)
![C:\Users\Administrator\AppData\Roaming\Tencent\Users\2264530805\TIM\WinTemp\RichOle\]MEA`Z[G2B5L)T01MJM66BV.png](http://www.biyelunwen.org/wp-content/uploads/2020/02/lw4299_2020218103816365.png)