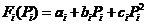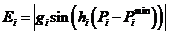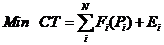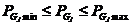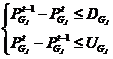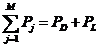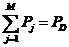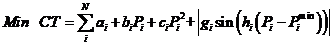电力系统经济负荷分配智能算法优化研究毕业论文
2020-02-18 11:00:29
摘 要
本文首先建立了带阀点效应的经济负荷分配数学模型,详细地分析比较了遗传算法和差分进化算法之间的差异和优劣。采用差分进化算法五种不同的变异策略算法与传统的遗传算法,计算了分别在3、13和40机组经济负荷分配中各个机组的输出功率,分别经过 50次独立运行,通过对结果的相互比较,证明采用差分进化算法优化所求的解具有很高的稳定性。并且分析在解决不同维数问题时,差分进化算法不同变异策略的优劣性。实验结果表明,本文方法是一种有效解决大规模电力系统经济负荷分配问题的方案,可广泛应用于电力系统其他优化问题。
本文特色在于横向分析了差分进化算法的五种不同的变异策略,提出在使用差分进化算法解决低维数问题时可以优先考虑“DE/current-best/1”变异策略,解决高维数问题时可以优先考虑“DE/rand/1”变异策略。
关键词:经济负荷分配;阀点效应;差分进化算法;变异策略
Abstract
Firstly, a mathematical model of economic load distribution with valve-point effect is established, and the differences and advantages between genetic algorithm and differential evolution algorithm are analyzed and compared in detail. Five different mutation strategy algorithms of differential evolution algorithm and traditional genetic algorithm are used to calculate the output power of each unit in economic load distribution of 3, 13 and 40 units respectively. After 50 independent operations, the results are compared with each other, which proves that the solution optimized by differential evolution algorithm has high stability. And the advantages and disadvantages of different mutation strategies of differential evolution algorithm in solving different dimension problems are analyzed. The experimental results show that the proposed method is an effective solution to the economic load distribution problem of large-scale power system, and can be widely used in other optimization problems of power system.
In this paper, five different mutation strategies of differential evolution algorithm are analyzed horizontally. It is proposed that DE/current-best/1 mutation strategy can be given priority when using differential evolution algorithm to solve low-dimensional problems, and DE/rand/1 mutation strategy can be given priority when solving high-dimensional problems.
Key words: economic load distribution; valve point effect; differential evolution; mutation strategy
目 录
摘 要 Ⅰ
Abstract Ⅱ
第1章 绪论 1
1.1 研究背景与目的 1
1.2 国内外研究现状 2
第2章 经济负荷调度问题的数学模型 5
2.1 阀点效应的数学模型 5
2.2 经济负荷的约束条件 6
2.2.1 发电机的运行约束 6
2.2.2 机组出力爬坡约束条件 6
2.2.3 电力平衡约束条件 6
2.3 建立经济负荷分配问题数学模型 6
第3章 智能算法原理分析 8
3.1 智能算法背景 8
3.2 差分进化算法与遗传算法的差异 8
3.3 差分进化算法概述 9
第4章 差分进化算法求解ELD问题 12
4.1 求解3机组经济负荷分配问题 12
4.2 求解13机组经济负荷分配问题 13
4.3 求解40机组经济负荷分配问题 16
4.4 本章小结 19
第5章 总结与展望 20
5.1 本文总结 20
5.2 未来展望 20
参考文献 21
致 谢 22
第1章 绪论
1.1 研究背景与目的
随着市场经济的蓬勃发展,电力产业也成为了国民经济的重要部分,我国人民生活水平和需求的日益提升,对于电力需求量的增加也是情理之中。电力系统面临着调峰困难,电网建设落后等实际性的困难,所以当务之急需要增强电网对于电力生产的规模,以及扩大电力建设的规模。电力产业对国民经济和国家发展有着巨大的影响力,仅国家电网一家在2018年全球企业榜中就排名第二位,所以对于电力系统规划分配的任务研究是当前电力研究的重点,对于社会发展有着重大的现实意义。
电力系统规划分配中,经济负荷调度(ELD)是重要的内容之一,其的主要任务就是满足安全和一定质量要求的条件下得出最符合经济性、环保性的负荷分配方案,即合理地利用现有的能源和设备,以最小的运行成本和环境成本来满足用户对于电力的需求。它不仅关系到能源消耗, 而且对环境污染和环境保护具有重要意义。在火力发电厂,为了最大限度地减少燃料消耗,同时满足需求和运行限制,对发电机组进行优化,可以经济地运行电力系统,并减少SO2和NOx等污染物的排放[1]。
电力系统是一个复杂的整体结构,其数学模型难以表达,一般的优化算法只能够胜任求解凸函数,线性系统的任务。而所需要进行计算的电力系统积极负荷一般都为大规模的非凸非线性系统,这种情况下一般的算法难以进行直接的计算,为了得到最后的结果,通常要对求解的精度和约束条件的要求进行折中,例如对于非线性系统,可以强行将其线性化,或是选择性的忽略一些影响因素比较小的约束条件来达到求解的目的。但是这些操作难免都会带来误差,最终导致处理大型系统时初值无法确定,最终算法难以收敛。非线性规划对于函数的连续性要求很高,甚至有些算法要求函数可导,但是如果简单将不连续变量通过函数计算进行规整,难免会产生一定的误差。还有很重要的一点,非线性规划很容易陷入局部最优解中,有时全局最优解和局部最优解之间差距有可能会非常大,从而导致规划的对象投资增大。另一方面,规划问题本身拥有很高的复杂性,我们难以对优化函数的所有特性做出全面的把握,因此寄希望于简单的通过设置初值的方式求得全局最优解是不合实际的。在实际应用中,使用动态规划引入各种约束条件,可以考虑离散变量和随机因数,在理论上动态规划能真正获得最优整体方案,但是也仅仅局限于低维数的问题,当处理大规模问题,很容易陷入维数灾难[2]。
由此可见,电力系统规划的困难主要存在于两个方面:首先就是对复杂的非凸、非线性规划问题缺乏有效的求解工具;其次是根据不同的电力工业模式,需要建立不同的求解模型。
经济负荷分配是一个复杂的问题, 一直都受到国内外学者的普遍关注,它具有成本函数、阀点效应、传输损耗和禁止区域,同时,它还有高维、非线性、不可微分和多约束等特点。传统上, 经济负荷分配问题的成本函数是用二次函数描述的, 并使用拉格朗日乘法器、线性规划、动态规划等数学方法求解。然而,这些数学方法要求目标函数是连续的和可导的。在解决ELD问题时, 这些方法容易陷入局部最优,收敛速度慢,难以较好地解决经济负荷分配问题。
1.2 国内外研究现状
相较于国内,国外在这方面的研究较早,并且着力于研究优化理论算法,其中最主要的有线性规划法,等微增法,动态规划法,拉格朗日松弛法等。近年来,随着人工智能算法的发展,一些学者又提出了将人工智能算法应用于电力系统的经济负荷优化调度问题中,其中较为突出的算法有遗传算法,粒子群算法,混沌算法,模拟退火算法,粒子群优化算法,免疫算法等。在实际系统开发方面,德国西门子公司编译的负荷优化软件在德国、韩国等国家都有了相对成熟的应用[3]。
此外,在一些发达国家,自上个世纪八十年代以来,他们在经济负荷优化调度问题上[4]。尤其随着全球经济的发展,在全球范围内,全球电力市场开始大刀阔斧进行改革,电力市场呈现一种百花齐放的态势,电力企业过去一家垄断的格局不再,电力行业开始呈现生机勃勃的竞争场面。
由于经济负荷调度优化对提高发电企业的经济效益和改善机组系统安全运行有着至关重要的作用,因此,国内外学者已经对ELD问题的难点进行了大量的理论研究,并对此提出了许多行之有效的解决方案。B. El-sobky, Y. Abo-elnaga, A. Elsaid和A. Foda提出了一种求解非线性约束多目标优化问题的新算法。该算法将一个多目标问题转化为一个单目标问题,基于I-SHOT和STEM方法的混合方法,将其称为松弛-顺序混合优化技术。将单目标约束优化问题转化为无约束优化问题,采用主动集策略和罚分法相结合的方法。在算法中加入期望域全局策略,解决了获得的无约束问题,保证了全局收敛性。该算法在标准的IEEE30总线6发电机测试系统上进行了测试。将所提出方法的结果与文献报道的结果进行比较。比较表明,所提出的算法有效地解决经济负荷分配问题。Leena Daniel, Krishna Teerath Chaturvedi和Mohan Lal Kolhe提出了一种时变动态经济负荷调度模型,在该模型中,对每一特定的时间间隔进行负荷调度计算,首先用传统的lambda迭代技术对其进行测试,然后将结果用于训练人工神经网络,该模型是基于Levenberg-Marquardt算法,与其它算法相比,该模型具有较好的性能。Farid Mohammadi和Hamdi Abdi提出了一种改进的乌鸦搜索算法,该算法通过对乌鸦的创新选择和飞行长度的自适应调整来改进乌鸦搜索算法。改进的乌鸦搜索算法是一种基于群体的技术,基于乌鸦在寻找食物来源时的智能行为。在改进的乌鸦搜索算法中,每只乌鸦都会在需要的时候把食物藏在隐蔽的地方。此外,每只乌鸦都会在环境中寻找更好的食物,它们会跟随其他乌鸦去它们的藏身之处。提出改进的乌鸦搜索算法在原有的乌鸦搜索算法中发展了乌鸦的搜索能力,并引入了一种乌鸦选择目的地的新方法。为了说明改进的乌鸦搜索算法在经济负荷分配问题中的适用性,将其应用于五种不同的知名测试系统。从求解质量、鲁棒性和计算时间等方面与其它方法进行了比较,表明该方法具有比其它方法优越的性能[5]。
在上个世纪五十年代,我国就在电力负荷调度方面开始进行了研究,提出了 “等微增率”负荷调度,但是这种算法局限性太大,随着电网规模的迅速发展,这种方法难以处理复杂程度大大上升的电网系统,想仅仅依靠人工的计算得到优化的最优解显然是十分困难的,所以对于机组调度优化问题的研究具有重大的现实意义。近年来,电力市场的不断发展、改革,机组的优化调度问题在国内也引起了各电力系统部门和学者的重视。
华中科技大学的侯云鹤、鲁丽娟、程时杰等人提出了一种改进的广义蚁群算法,能够顺利应用于复杂的非凸、非线性电力系统经济负荷分配问题。这种改进的粒子群算法是一种通用的优化算法,在处理约束条件非线性化、目标函数非凸的问题是收敛性很好,且容易实现并行运算。基于随机分析理论,证明了该算法依概率收敛至全局最优,且收敛性于粒子群的初始分布无关[6]。
四川大学的邱晓燕,李锐,孟鹏提出了一种自适应遗传算法解决微电网负荷优化分配,其微电网数学模型考虑了运行的约束条件、负荷需求、微电源的燃料消耗、维护成本与启动成本,以及动态的网络损耗和购电、售电价格等等,运用基于市属编码的改进自适应遗传算法对模型进行求解,结果验证了此种算法在微电网中应用的有效性[7]。
上海交通大学的王昕,邓益慧等人将改进的人鱼群算法应用于机组负荷优化中,解决了传统人工鱼群算法计算到全局最优解时速度变慢,搜索效率降低的问题,更快更准确地获取全局最优解[8]。
东南大学的刘飞龙、司风琪、韩朝兵将负荷优化分配在电网与发电厂两个层次进行分解,建立了网、厂两级负荷优化分配模型,并采用自适应惯性权重和混沌优化搜索方法,算法有较高的效率[9]。
广西大学的陈碧云,韦杏秋,陈绍南,刘柏江提出一种基于交互式多目标处理方法的多种群遗传算法来解决电力系统经济问题中的多目标问题。该算法通过追求最小总体协调度,即寻求满足总体协调度的最短“欧氏距离”,来获得决策者的满意理想值;算法还引入精英策略和移民策略,提高寻优范围和效率,且能有效克服标准遗传算法通过迭代次数终止迭代、易早熟的缺陷。此算法在解决多目标、非线性和多约束问题上有着较强的全局收敛能力[10]。
安徽电力调度控制中心的李有亮提出了一种改进的自由搜索算法,该算法借鉴了高等群居动物的活动行为,同时兼备了各种演化算法的优点,具有较高的智能性。其算法在搜索半径内自适应调整,结合其他优化算法的交叉操作、精英保留策略,最终获得全局最优解[11]。
目前为止,实际负荷优化系统的开发也引起了各个企业的广泛关注,清华同方电子有限公司,西安热工研究院等研究机构都在积极响应行业号召,加入到系统研发制作中。值得一提的是,北京华电天仁电力控制技术有限公司开发的负荷优化分配系统模块已在中电神头第二发电厂有着较为成功的应用。这预示着我国在荷优化系统的开发已取得阶段性成功。
我国电力需求量不断地增加,随之电网中负荷峰谷差也不断增大,对于电力调峰的操作也愈加困难。在上个世纪电网建设并不发达的时期,调峰任务一般只需要使用中小容量的老机组就能够胜任,这些机组在当时基本能够满足调峰的需要,且操作比较简单,启动和停机的速度都较为快速。但进入新世纪,由于电网建设进程突飞猛进,峰谷差的增大使得中小容量的老机组已经无法参与调峰,这促使着一批较大容量机组开始得到应用,如我国的300MW机组已经开始低负荷运行调峰,而以前的一些中小型容量机组也随之走下历史舞台。尽管我国将大容量机组参与调峰,但实质并没有制造专门用于调峰的单元汽轮机,而是基本负荷机组改造的降负荷运行,所以在负荷峰谷差不断增大的情况下,我国电网的调峰面临的问题更加严峻。
现阶段,我国对负荷分配优化的研究还集中在对于算法的改进和模型的修正上,而往往忽视了一些值得研究的影响因素,例如结合机组的机械特性,或者负荷的动态特性同样值得研究。目前,一些国内学者也开始研究应用多目标的优化方法实现机组负荷的优化分配,考虑多个目标的负荷优化分配使优化结果更符合实际工程需要。
第2章 经济负荷调度问题的数学模型
2.1 阀点效应的数学模型
经济负荷调度问题是在电力负荷和电力系统安全的情况下,通过合理分配机组的输出, 最大限度地降低火电厂的总成本。该单元的燃料成本数学函数与发电机的参数有关,国际电工学会推荐使用二次函数拟合[12],将机组耗量曲线表示如下:
| (2.1) |
其中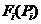 和
和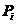 分别为燃料成本和第i台机组的输出功率。
分别为燃料成本和第i台机组的输出功率。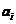 ,
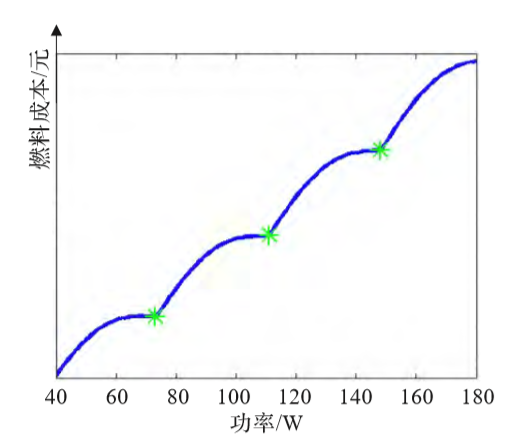
,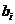 和
和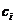 是该单元的成本参数。
是该单元的成本参数。
 在实际系统中, 除了机组的燃油成本影响电力系统的成本外, 还有许多因素对电力系统的成本产生影响,如输电损耗、油耗特性、阀点效应、ELD约束条件等。在这些因素中, 阀门点效应对优化精度有很大影响。当发电机的进气门突然打开时,会对发电机的消耗特性曲线产生波纹效应。这就是所谓的阀点效应[13]。在考虑阀点效应时,发电机的消耗曲线如图2.1所示。
在实际系统中, 除了机组的燃油成本影响电力系统的成本外, 还有许多因素对电力系统的成本产生影响,如输电损耗、油耗特性、阀点效应、ELD约束条件等。在这些因素中, 阀门点效应对优化精度有很大影响。当发电机的进气门突然打开时,会对发电机的消耗特性曲线产生波纹效应。这就是所谓的阀点效应[13]。在考虑阀点效应时,发电机的消耗曲线如图2.1所示。
图2.1 计阀点效应的消耗曲线
忽略阀点效应会明显影响燃料成本结果的精度。因此第i个单元的阀点效应可以定义为:
| (2.2) |
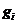 和
和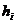 是二量单元的阀点效应系数。具有阀点效应的ELD问题的数学模型函数可由(2.3)给出。
是二量单元的阀点效应系数。具有阀点效应的ELD问题的数学模型函数可由(2.3)给出。
| (2.3) |
在式(2.3)中,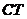 是电力系统的总成本, N是电力系统中单位承诺的数量。本文针对ELD问题,忽略了电力系统的传输损耗,并考虑了三个主要约束条件。
是电力系统的总成本, N是电力系统中单位承诺的数量。本文针对ELD问题,忽略了电力系统的传输损耗,并考虑了三个主要约束条件。
2.2 经济负荷的约束条件
2.2.1 发电机的运行约束
在电力系统的经济符合分配问题中,必须考虑到发电机的约束条件,即
| (2.4) |
式中,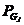 、
、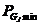 、
、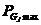 分别为发电机有功出力及其下限与上限。负荷分配的结果必须保证各个机组所发出的有功功率在其规定的有功出力上下限之间。
分别为发电机有功出力及其下限与上限。负荷分配的结果必须保证各个机组所发出的有功功率在其规定的有功出力上下限之间。
2.2.2 机组出力爬坡约束条件
爬坡约束是与时间相关的微分型约束问题:即供电网在供电时,电力需求每时每刻都处于动态变化中,为了保证供电系统的稳定性,提高电网的响应速度,发电机组(发电厂)在相邻两个时间段内的有功功率差值不应大于该机组在此时段内所能升功率或能降功率的最大值,即
| (2.5) |
式中,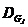 为机组j在相邻时段出力容许的最大下降值;
为机组j在相邻时段出力容许的最大下降值;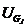 为机组j在相邻时段出力容许的最大上升值。
为机组j在相邻时段出力容许的最大上升值。
2.2.3 电力平衡约束条件
电力平衡约束是指发电机的有功功率之和等于系统总负荷与总网损之和,即
| (2.6) |
式中: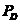 为系统总负荷,
为系统总负荷,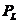 为系统总网损。网损一般采用潮流法及B系统数法求得。当电力系统覆盖密集是可以忽略网损,本文在计算中忽略了网损,故电力平衡约束条件可以简化为
为系统总网损。网损一般采用潮流法及B系统数法求得。当电力系统覆盖密集是可以忽略网损,本文在计算中忽略了网损,故电力平衡约束条件可以简化为
| (2.7) |
2.3 建立经济负荷分配问题数学模型
根据前文所建立的数学模型,当考虑进气门打开时的阀点效应,不考虑网络损耗的前提下,目标函数为:
| (2.8) |
同时约束条件满足式(2.5)(2.7)。
第3章 智能算法原理分析
3.1 智能算法背景
模拟自然选择、突变和遗传运算的智能进化算法(IEA)本质上是多维并行性。它不需要目标函数是连续的和可导的。它适用于解决非线性和不可微分的问题, 在解决这些问题方面具有良好的性能和鲁棒性。因此,近年来,国际能源机构经常被用来解决ELD问题。
差分进化算法(Differential Evolution,DE)由Rainer Storn和Kenneth Price于1996年为求解切比雪夫而提出,其也属于进化算法的一种,利用实数编码求解优化问题。该算法通过初试种群的不断随机进化从而达到全局搜索最优解的目的,因其易用性、稳健性和强大的全局寻优能力而为大众所知,并被广泛应用在数据挖掘、约束优化、聚类优化、非线性优化控制、神经网络优化、滤波器设计和天线方向图等领域[14]。在被提出当年的ICEO竞赛中,差分进化算法脱颖而出成为全场运算最快的算法。