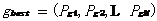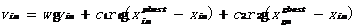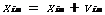粒子群优化算法在移动机器人路径规划中的应用毕业论文
2020-02-18 11:57:35
摘 要
在过去的几十年中,移动机器人作为一种实用度极强的无人驾驶机器设备,在多个领域都有着极大的应用市场。为机器人规划出一条可行路径,是实现其功能的基本保证,也是机器人领域研究的一个最基本、最关键的问题。鉴于路径规划的重要性,在过去的几十年中,移动机器人路径规划获得了越来越多的研究兴趣,机器人的各项性能也越来越得到重视。如何令机器人在工作空间中安全高效的工作也成为了该领域中有待钻研的问题。移动机器人想要获得较高的使用安全性,首先要考虑的问题就是避障问题,即如何在复杂的工作环境中为机器人规划出一条安全的、可避开所有障碍的路径。这对于提高机器人工作的安全性具有重大意义。因此,也成为本论文研究的基本出发点。
本文旨在利用粒子群优化算法为移动机器人在复杂工作环境下规划出一条安全的避障路径。粒子群优化算法可以这样描述,通过预设的粒子(个体)之间的相互交流合作来寻找全局最优解。它应用在路径规划中是十分有效的,可以通过仿真验证其有效性和可行性,并且可以通过对算法的改进,不断的缩短寻找最优路径所需时间,不断的提高所寻路径的安全性。
关键词: 粒子群算法 移动机器人 路径规划 可行性规则
ABSTRACT
In the past few decades, mobile robot, as a highly practical unmanned machine equipment, has a great application market in many fields. Planning out a feasible path for robot is the basic guarantee to realize its potential basic functions, and it is also the most basic and key problem in robot research. In view of the importance of path planning in the past few decades, mobile robot path planning has gained more and more research interest, and the performance of robots has been paid more and more attention. How to make robots work safely and efficiently in the workspace has also become a problem to be studied in this field. In order to obtain higher safety, the first problem to be considered for mobile robot is obstacle avoidance, that is, how to plan a safe path for robot to avoid all obstacles in the complex working environment. This is of great significance to improve the safety of robot work. Therefore, it also becomes the basic starting point of this paper.
This paper aims to use particle swarm optimization (pso) to plan a safe obstacle avoidance path for mobile robots in complex working environments. Particle swarm optimization algorithm can be described by the preset mutual exchanges and cooperation between the particles (individual) to find the global optimal solution, used in path planning is very effective, and can verify its validity and feasibility through the simulation, and can be modified through the algorithm, continuously shorten the time required to find the optimal path, constantly improve the security of the search path.
KEY WORDS: Particle Swarm Optimization, Robot,Path Planning, feasibility principle
目录
第1章 绪论 1
1.1 研究背景及意义 1
1.2 国内外研究现状 1
1.3 课题的研究方法及内容 3
第2章 基本粒子群算法 4
2.1 粒子群优化算法简介 4
2.2 粒子群算法基本思想 4
2.3 基本PSO算法模型 5
2.4 粒子群算法参数分析 8
2.5 基本粒子群算法的缺陷与参数改进法则 9
2.6 本章小结 12
第3章 粒子群算法在移动机器人路径规划上的求解 13
3.1 引言 13
3.2 移动机器人路径规划的基本问题 13
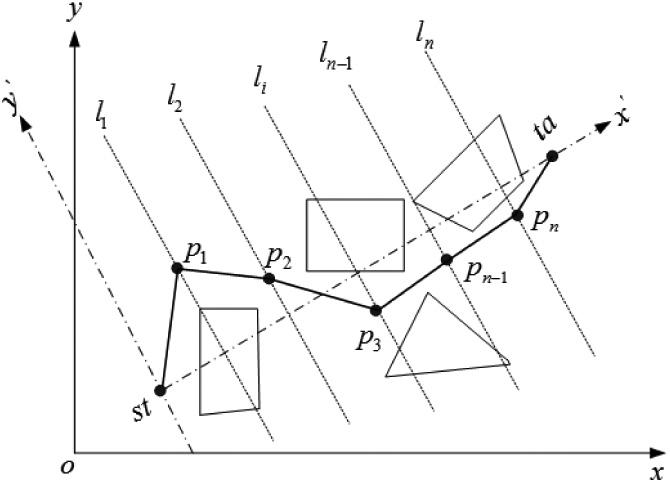
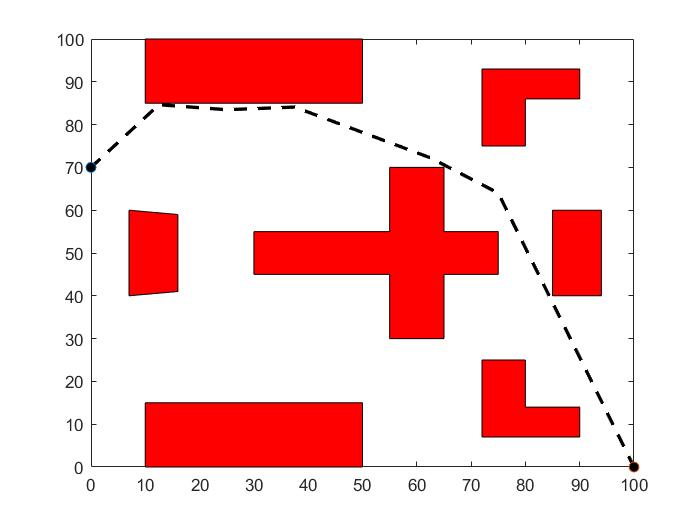
3.3 工作空间的建模 14
3.4 移动机器人路径规划问题建模 15
3.5 约束条件的处理 16
3.6 本章小结 18
第4章 仿真及数据分析 19
4.1 引言 19
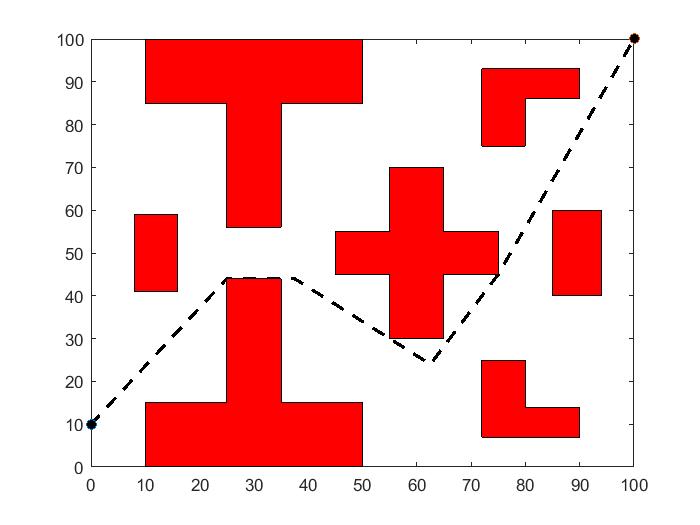
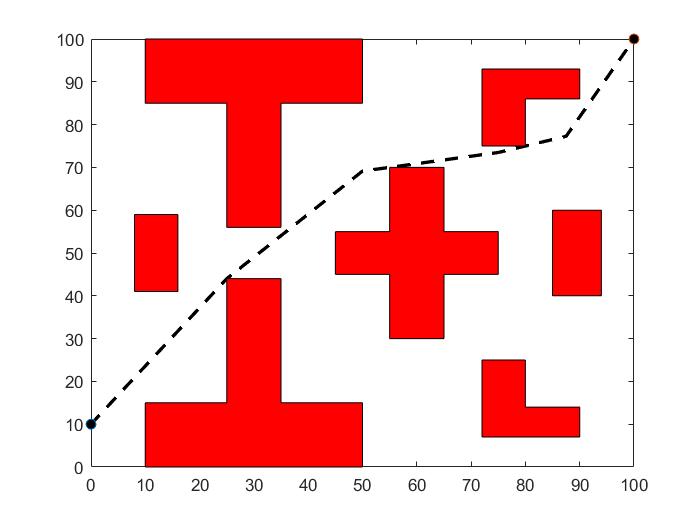
4.2 数值仿真1 19
4.3 数值仿真2 21
4.4 数值仿真3 23
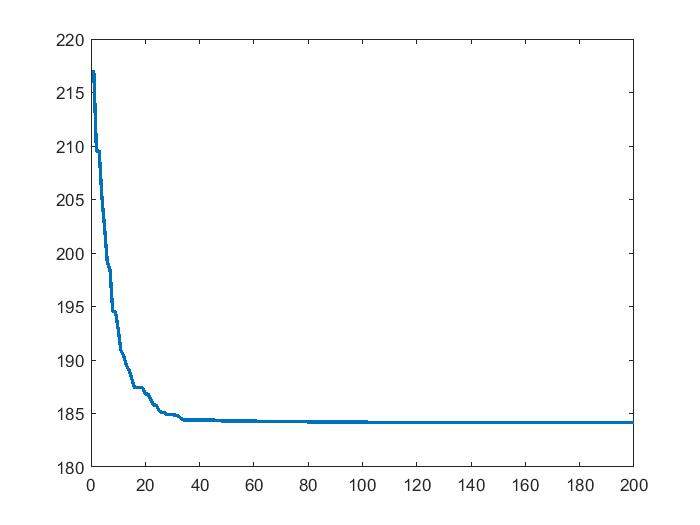
4.5 数据处理 25
4.6 本章小结 26
第5章 总结与展望 27
参考文献 28
致谢 29
第1章 绪论
1.1 研究背景及意义
随着时代的不断发展,越来越多的特殊工作环境随着工业的进步而出现,所以机器人的存在变得极为重要。移动机器人作为一种实用性极强的无人驾驶的机器人设备,在工业领域有着不可估量的发展潜力。移动机器人(Mobile Robot,MR),本质上是一种自动执行工作的机器装置。通常在人类预先设定的程序控制下行动,同时机器人的行动也要遵守科学家制定的原则纲领。移动机器人的主要任务之一就是在特定的场合做特定的工作。在生产行业、建筑行业,或是危险的军事环境,移动机器人具备优秀的移动能力,在代替人类进行危险,恶劣(如辐射环境下,有毒气体环境下)环境下作业和人类难以进入的(狭小空间,涵洞,水下)环境作业相较于普通机器人有着更大的机动性以及灵活性,所以为移动机器人规划出一条避障的路径对提高移动机器人工作的安全性具有极大意义,存在很大的研究价值。
导航技术一直以来都是移动机器人研究中的核心问题,其中不可忽视的一个环节便是其路径规划问题。无论机器人使用哪一种方法进行导航工作,都离不开路径规划这一核心问题,所以该问题也被诸多研究人员所重视。
路径规划问题是指被规划目标按照某一特定的要求例如路径长度,所需时间或所消耗能量去搜索路径,其实就是在特定要求下寻得特定起点到终点的最优无障碍路径。路径规划首先要根据问题中已知条件和环境信息建立合理的模型,再利用可以使用的算法寻得从起点到终点的最有无障碍路径。较好的算法还可以最大程度地解决规划中的不确定因素和结果的误差,使机器人受到最小的其他因素的影响。在全世界研究人员的共同努力下,移动机器人路径规划的成果在不断的增多,许多难题也已经被陆续攻克。
本文旨在利用粒子群算法为机器人在较为复杂的工作环境下规划出一条无碰撞最优路径。粒子群优化算法(Particle Swarm optimization,PSO)是模拟自然界中鸟类种群寻找食物的群体行为的起来的一种算法,它是一种基于种群中个体协同合作的随机搜索算法。在算法中,优化问题的每一个解都类似于自然界中鸟类种群的一个个体,通过迭代寻找移动机器人的任务问题中的最佳路径。
1.2 国内外研究现状
近些年来,随着机器人行业的飞速发展,国内外的研究者们对于粒子群优化算法在移动机器人路径规划中的应用也变得越来越成熟,所以大多数的研究者们都在不断的寻找一种令移动机器人自我进行路径规划的方法。首先对障碍环境进行建模,再选用粒子群优化算法作为规划所用算法,得到移动机器人在特定工作环境中的最优无障碍路径。
戴博,肖晓明等人提出针对于特定环境的路径规划方法,方法主要有以下两种:首先是环境整体的全局规划,即知道全部的环境信息;另一种是局部规划,即有部分环境信息未知[1]。于红斌,李孝安提出要想求得对于特定环境的路径规划的最优解,要尽可能掌握详细的全局信息[2]。到目前为止,各国学者已经对全局路径的规划问题提出了许多解决方法,但这些方法大多数受到机器人信息存储方式和路径规划时间的约束,计算量较大,实时性较差,无法很好的应用于全局路径规划问题。如何对全局路径规划方法做出新的改进,能在较短的时间内规划出最优的避障路径,是许多学者一直以来的研究目的所在[3-4]。
最初由国外两位著名学者Eberhart和Kennedy提出了粒子群优化算法(Particle Swarm optimization,PSO)。作为一种模拟自然界鸟类种群寻找食物时的飞行模式的仿生算法,PSO算法具有多个优点,其使用简单,鲁棒性较好,算法收敛速度较快,对于预设种群的规模也没有较高的要求,所以在移动机器人路径规划中十分实用[5]。
国内学者秦元庆,孙德宝等人首次将PSO引入到移动机器人路径规划中来,该方法首先使用迪杰斯特拉算法求得链接图的最短路径,然后引入PSO,其作用是对寻得路径中所有的节点位置进行二次优化,实现路径的两次优化[6]。但由于秦等人所做的研究无法完全体现环境的全部信息,所以最终优化过的路径不一定是全局的最优路径。该方法的缺点在于一定程度上限制了PSO的全局寻优能力。
随后移动机器人路径规划也有了具体的定义,指机器人在工作环境中能够自动寻得最优得无障碍路径进行躲避障碍。针对于优化准则从初始点到目标点的无障碍碰撞的最优路径搜索[7],也印证了这样一种思想。粒子群算法应用于路径规划后,是将自然界生物群落信息交流共享的进化思想转变为路径规划中每个粒子个体通过相互合作与信息交流来寻找全局路径得最优解[8]。
近些年来,传统的粒子群算法在移动机器人路径规划问题中已经取得了许多成果。但是传统的粒子群优化算法有早熟收敛的特点,很容易陷入局部最优解,并且有收敛速度慢的问题。在某些情况下不容易找到全局最优解来支持移动机器人的路径规划。西安科技大学的李珊曾利用粒子群优化算法对移动机器人路径规划问题进行了多方面的研究:将一个新的因子项加入到粒子的速度更新公式当中去,这一新的因子项被称为“进步因子项”,并把实验中超出初始空间的粒子统一处理,进行随机初始化,这样就可以提高所寻得最优解的质量。但是该研究有这样一个缺点,实验选取了较为简单的全局环境,不具备实际的工作情况[9]。燕山大学的李宝霞引入模糊算法辅助,对移动机器人的路径规划做出新的研究,但是仿真时,实验过程同样不具备实际的工作情况[10]。
考虑到粒子群算法和移动机器人路径规划有着一种本质上的关联,本文使用粒子群算法进行移动机器人路径规划,并将根据基础算法的缺陷进行算法的改进,以提高寻得最优路径的质量,并通过仿真验证其可行性。
1.3 课题的研究方法及内容
本文已改进的基本PSO算法为基本工具,主要针对移动机器人路径规划问题开展研究工作。
第一章 主要阐述本文得研究背景及意义,对移动机器人路径规划及粒子群算法的国内外研究现状作出了阐述,同时简单阐述文章组织结构。
第二章 主要对基本PSO算法进行改进,从基本粒子群算法的基本思想及原理开始介绍,随后阐述其重要参数及算法模型,最后结合算法缺陷进行改进,提出改进法则。
第三章 将粒子群算法应用在移动机器人路径规划问题中进行求解,首先进行工作空间的建模,然后对移动机器人路径规划问题进行建模,并列出其约束条件。
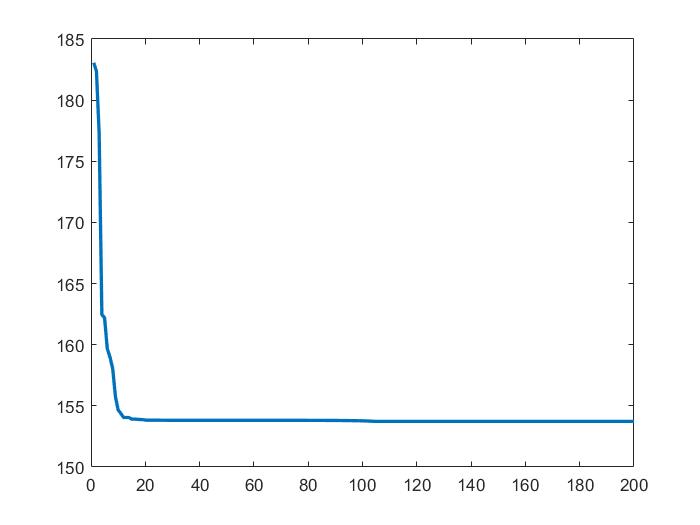
第四章 进行仿真及数据分析,对基本PSO算法和改进PSO算法仿真进行对比,并通过数据处理分析对比结果。
第五章 总结本文的研究工作,并对今后的研究工作进行展望。
第2章 基本粒子群算法
2.1 粒子群优化算法简介
粒子群算法(PSO),也被称为粒子群优化算法。该算法实质上其实是一种进化计算技术(evolutionary computation),算法大概有二十几年的历史,最早在1995年由Eberhart和kennedy两位博士提出。粒子群算法的开创源于研究者们对大自然中鸟群捕食行为的研究,是人们受到自然界中鸟类种群活动特性的启发后,基于群体智能创建的一种简化模型。PSO的起源是模拟鸟群的捕食行为,在自然界中有这样一个场景:在随机的自然环境中,有一群鸟在该环境下无目的性的随机搜寻未知地区的食物。整个区域内有且仅有一块食物,即只存在一个最优解。所有的个体都不知道最优解在哪一个区域,但是有这样一个已知条件,所有的鸟都掌握着这样的信息,自己距离食物的距离,自己此时的具体位置。那么对于所有个体来说,搜寻目前距离食物距离最短的鸟的周边区域是找到该空间中唯一食物的最快方法。
从自然界中鸟类种群觅食过程中得到启示的PSO算法可以很好的使用在优化问题的解决中。在算法中,优化问题的每一个解都可以看作自然界鸟类种群中的一只鸟,优化问题的解的集合就是整个鸟群,每一个粒子都拥有一个自己的适应值,值由一个被优化的函数决定。每个粒子在搜索空间中所飞行的距离和方向由粒子本身的速度决定,最后,整个搜索空间中的全部粒子就根据当前时刻处在最优位置的粒子在整个空间中进行搜索。
本章从粒子群算法的起源出发,对基本算法进行详细的介绍,其中内容包括算法的基本法则,原理,参数分析,框图等,并根据基本PSO算法的缺陷进行改进。
2.2 粒子群算法基本思想
一直以来科学家对自然界中动物的群体行为都有着浓厚的研究兴趣,粒子群算法最初的研究思想同样来源于此。著名的生物学家,计算机图形学家Craig Reynolds曾开发出正则计算模型(类鸟程序 birds program)。当时该模型通常被用于影视作品的特效制作中,他曾经在1987年提出了一个著名的在所有鸟群研究领域十分著名的的鸟群聚集模型,在他所构造的仿真环境中,每一个个体遵循以下三条原则:
- 首先避免与邻域个体相冲撞;
- 所有个体匹配邻域个体的速度;
- 被选中个体飞向鸟群中心,并且整个群体飞向目标。
在仿真中仅仅使用这三条简洁的原则,就可以模拟十分接近自然界中鸟类种群飞行的现象。粒子群算法基本思想的确立,就是受到了自然界中鸟类群体行为的启发,对其进行了系统的研究,不断的建立环境模型并仿真。他们主要对Frank Heppner的模型进行了修正,使得尽可能多的粒子进入解空间并寻求最优解。
使用粒子群算法时,首先初始化一个粒子种群,种群内含有随机数量的粒子,然后通过数学中的迭代计算寻找所需的最优解。在每一次的迭代中,粒子通过这样的方式来更新自己的位置及速度。在PSO算法中,有两种极值的存在,每一个粒子自身所能寻到的最优解,我们通常称作个体极值(pbest)。另一个极值是整个粒子群中所有粒子所能寻到的最优解,就是全局极值(gbest),这两个值便是粒子更新的参照依据,每一个粒子在整个空间中的速度会不断的改变,以确定自身下一步的走向,并尽可能的向着两个极值所指向的解空间移动。
在利用PSO算法求解某些优化问题时,一般需要遵守以下几个基本法则:
- 邻近法则:该法则要求种群具有一定的时空计算能力,即在一定的计算时间里,该法则要求种群对搜索的环境具有一定的计算和分析能力。
- 品质法则:在粒子种群对搜索环境的复杂度进行计算后,该法则要求群体能够 对环境的质量或品质做出评估。评价群体中每个个体的最优适应值和群体的全局适 应值是该法则的具体体现。
- 多样性法则:为了搜索到品质更好的解,该法则要求群体中的粒子在搜索的初 期尽量分布在搜索环境的不同地方,而非过分地集中于某些局部的搜索环境。
- 稳定性法则:稳定性法则要求群体的搜索行为具有一定的鲁棒性,即要求群体 中的每个个体或者大部分个体在搜索的过程中尽量保持类似的搜索行为。作为一种 随机搜索算法,PSO算法的稳定性对算法的性能有着重大影响。PSO算法的收敛性是 稳定性法则的一个最具体体现。
- 适应性法则:在有限的计算时间多项式里,适应性法则要求群体中的每个粒子 都具有自适应调整各自搜索行为的能力。动态调整粒子的全局和局部搜索能力是该法则的一个重要体现。
2.3 基本PSO算法模型
粒子群算法模型可以这样形象的描述:在一个我们预设的空间中,有这样一群粒子,他们是没有质量体积的质子,粒子之间可以相互交流信息,进行个体间的合作,通过不断的寻找,交流,确定最后的解区间,并且通过我们对参数的调整可以不断的寻求最优解。
在基本PSO算法中,群体中的每个个体称为一个粒子,代表待优化问题的一个潜在解。对于一个n维优化问题,每个粒子被赋予一个速度和位置向量,分别表示为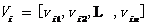 和
和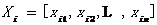 。在搜索的过程中,每个粒子根据自身的搜索动态和群体中其他粒子的搜索动态调整各自的运动状态,从而保证每个粒子逐步向问题的最优解方向靠近。为了直观的展现算法的粒子公式,我们可以假设一种情景:
。在搜索的过程中,每个粒子根据自身的搜索动态和群体中其他粒子的搜索动态调整各自的运动状态,从而保证每个粒子逐步向问题的最优解方向靠近。为了直观的展现算法的粒子公式,我们可以假设一种情景:
假设有一个M维的目标搜索空间,其中有一个由N个粒子组成的群落,其中第i个粒子在M维空间里的位置表示为:
| (2.1) |
第i个粒子在M维空间里的飞行速度表示为:
| (2.2) |
适应值表示为:
| (2.3) |
第i个粒子目前搜索到的最优位置我们将其称为粒子的个体极值,表示为:
| (2.4) |
整个粒子群目前为止可以搜索到的最优位置则被称为全局极值,表示为:
| (2.5) |
其第m维分量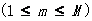 将会有如下公式,并根据下列公式进行变化:
将会有如下公式,并根据下列公式进行变化:
| (2.6) | |
| (2.7) |
其中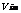 表示粒子i飞行速度矢量的第m维分量,
表示粒子i飞行速度矢量的第m维分量,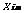 表示粒子i空间位置适量的第m维分量,
表示粒子i空间位置适量的第m维分量,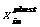 表示粒子i位置矢量的第m维分量整个空间中所经历的最好位置,
表示粒子i位置矢量的第m维分量整个空间中所经历的最好位置,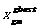 表示粒子群目前在解空间中所经历的最好位置。
表示粒子群目前在解空间中所经历的最好位置。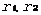 表示介于零到一之间的随机数,
表示介于零到一之间的随机数,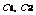 表示加速度系数,
表示加速度系数,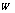 表示惯性权重。
表示惯性权重。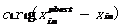 表示“认知项”(cognitive term),其实是粒子先前的速度,该项与粒子本身的认知经验有关,
表示“认知项”(cognitive term),其实是粒子先前的速度,该项与粒子本身的认知经验有关,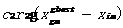 表示“社会项”(social term),是用来代表空间中所有粒子之间的空间信息共享和它们之间的相互合作。
表示“社会项”(social term),是用来代表空间中所有粒子之间的空间信息共享和它们之间的相互合作。
公式中的认知项表示了整个空间中所有粒子(个体)之间的竞争,社会项表示了整个空间中所有粒子(个体)之间的信息交流与合作,这样又回归到了仿生学的自然模型中。通过空间中所有粒子(个体)之间的竞争与合作,整个粒子群(种群)才能不断的向更优的趋势发展进化。回到算法中,所有粒子各司其职,又不乏竞争与合作,才能让整个问题的解决得到更好的令人满意的结果。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示:

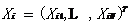 ,
,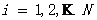
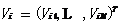 ,
,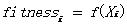
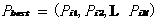 ,
,