6061铝合金粉末模压成形本构模型研究毕业论文
2021-03-11 23:19:30
摘 要
确定粉末成形材料的本构方程是揭示多金属混合粉末动态成形致密机理和规律的基础,对混合粉末进行压缩实验,建立6061铝合金混合粉末压制本构方程,探究Drucker-Prager Cap(DPC)模型方程中剪切曲面部分模型参数;帽屈服面部分模型参数与以及弹性模量E、泊松比v与相对密度的关系和摩擦系数μ与轴向力的关系,对研究其粉末压制成形规律、优化模具及工艺参数设计具有重要意义。
本文基于修正的Drucker-Prager Cap模型,对6061铝合金混合金属粉末进行轴向压缩实验,径向压缩实验以及单轴模压实验。根据轴、径向压缩实验两个实验过程中采集的载荷-位移曲线获得的压块破坏时的轴向压缩力和最大粉碎力,得到压块的轴向压缩强度和径向压缩强度,并确定了6061铝合金粉末的DPC模型中剪切屈服曲线,得出不同相对密度的参数摩擦角β和内聚力d。根据单轴模压实验测得粉末压制加载和卸载过程中上、下冲头应力—应变曲线和压模外壁环向应变,结合处理数据得到的静水压力p与等效应力q的关系,径向应力—轴向应力曲线和轴向应变—轴向应力,最终通过理论计算得到确定了修正的DPC模型帽型屈服曲线,得出不同相对密度的参数帽偏心率R、演变参数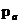 和静态压缩屈服应力
和静态压缩屈服应力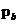 。结合三个实验的数据也得到不同密度的弹性模量E、泊松比v与摩擦系数μ。而且还探究了本构参数与压块相对密度之间的关系和摩擦系数与轴向力的关系,并得到了本构参数相对应的表达式和摩擦系数随轴向应力变化的规律 。
。结合三个实验的数据也得到不同密度的弹性模量E、泊松比v与摩擦系数μ。而且还探究了本构参数与压块相对密度之间的关系和摩擦系数与轴向力的关系,并得到了本构参数相对应的表达式和摩擦系数随轴向应力变化的规律 。
本文探究出了内聚力d、摩擦角β、帽偏心率R、演变参数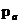 和静态压缩屈服应力
和静态压缩屈服应力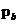 、弹性模量E、泊松比v八个参数与相对密度之间的关系;摩擦系数
、弹性模量E、泊松比v八个参数与相对密度之间的关系;摩擦系数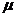 与轴向应力的关系这对6061铝合金粉末建立其密度相关的DPC模型有很大的帮助,对粉末成形过程中的模具设计和工艺参数具有重要意义。
与轴向应力的关系这对6061铝合金粉末建立其密度相关的DPC模型有很大的帮助,对粉末成形过程中的模具设计和工艺参数具有重要意义。
关键词:6061铝合金粉末;修正的Drucker-Prager Cap模型;本构参数;弹性模量;泊松比;摩擦系数
Abstract
Determining the constitutive equations of powder compaction is the basis of revealing metal powder compaction forming dynamic mechanism and law, doing the compression experiment,establishing the constitutive equations,studying the relationship between the parameters in the Drucker-Prager Cap (DPC) model,the elastic modulus E, the Poisson's ratio v and the friction coefficient and the relative density play an important role in the study of forming law and the optimization of die and parameters.
In this paper, the Drucker-Prager Cap model is presented to simulate the compaction behavior of 6061Al powders, and axial compression tests, radial compression tests and uniaxial single-ended compaction tests have been done. The axial compressive force and the maximum crushing force of the briquettes obtained during the two loads during the experiment are obtained by the load - displacement curve obtained by the axial and radial compression experiments. The axial compressive strength and the radial compressive strength of the compact are obtained,the shear yield curves of the DPC model of 6061 aluminum alloy powder were determined, and the parameters of friction coefficient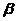 and cohesion of different relative density were obtained.According to the uniaxial compression test, the stress-strain curves of the upper and lower punctures and the circumferential strain of the outer wall of the die are measured during the loading and unloading of the powder.With the relationship between the hydrostatic pressure p and the equivalent stress q, the radial stress-axial stress curve and the axial strain-axial stress,the modified DPC model cap shape yield curve by theoretical calculation and the eccentricity R, the evolution parameter
and cohesion of different relative density were obtained.According to the uniaxial compression test, the stress-strain curves of the upper and lower punctures and the circumferential strain of the outer wall of the die are measured during the loading and unloading of the powder.With the relationship between the hydrostatic pressure p and the equivalent stress q, the radial stress-axial stress curve and the axial strain-axial stress,the modified DPC model cap shape yield curve by theoretical calculation and the eccentricity R, the evolution parameter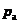 and the static compressive yield stress
and the static compressive yield stress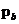 with different relative densities are obtained.The elastic modulus E, Poisson's ratio v and the friction coefficient of different densities are also obtained by combining the data of the three experiments. But also we explore the relationship between the eight parameters and the relative density of the briquettes.And the expressions of the constitutive parameters and the law of the friction coefficient with the axial stress are obtained.
with different relative densities are obtained.The elastic modulus E, Poisson's ratio v and the friction coefficient of different densities are also obtained by combining the data of the three experiments. But also we explore the relationship between the eight parameters and the relative density of the briquettes.And the expressions of the constitutive parameters and the law of the friction coefficient with the axial stress are obtained.
This paper explores the relationship between Cohesion d, friction angle β, cap eccentricity R, evolution parameter and static compression yield stress, elastic modulus E, Poisson's ratio v and the relative density; friction coefficient μ and the relative density.It is very helpful to establish the DPC model of 6061Al,and is important to mold design and process parameters of powder molding process.
Key Words: 6061 aluminum alloy powder;modified DPC model;Constitutive parameters;Elastic Modulus;Poisson's ratio;friction coefficient
目 录
摘 要 III
Abstract IV
第一章 绪论 1
1.1 研究背景 1
1.2 粉末成形的研究现状 1
1.3 课题来源 3
第二章 实验原理 5
2.1本构模型 5
2.2 参数的求解方法 7
2.2.1 摩擦角β、内聚力d的求解方法 7
2.2.2 帽形屈服面(R,pa,pb和α)参数的求解方法 9
2.2.3 弹性模量E、泊松比v的求解方法 11
2.2.4 摩擦系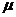 数的求解方法 13
数的求解方法 13
2.3 实验材料 13
2.4 实验设备 13
2.5 实验方法 14
第三章 单轴压缩和径向压缩(巴西圆盘)实验 16
3.1 实验工装模具 16
3.2 单轴压缩和径向压缩(巴西圆盘)实验过程 16
第四章 单轴模压实验 18
4.1 实验工装模具 19
4.2 单轴模压实验过程 20
第五章 实验数据处理和结果分析 22
5.1 内聚力d、摩擦角β 22
5.2 DPC帽型参数(R、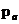 、
、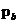 ) 24
) 24
5.2.1空压实验 24
5.2.2 实验数据预处理 24
5.2.3 径向应变转变为径向应力 25
5.2.4 DCP模型帽型参数求取 26
5.2.5 结果 27
5.3 弹性参数E、泊松比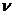 28
28
5.4 摩擦系数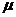 31
31
5.5误差分析 32
第六章 全文总结 33
参考文献 34
致 谢 36
第一章 绪论
1.1 研究背景
铝是地壳中其中一种分布最广泛的元素,排在氧元素和硅元素后面,位列第三位。但是对于金属元素来说,铝则是排在第一位。6061铝合金是Al-Cu-Mg-Si系铝合金的一种,密度低的同时,也有较高的强度与刚度。另外还具有很好的抗腐蚀性,良好的塑性和优秀的加工性能,价格低等优点。它普遍应用在各种强度高,耐腐蚀的工业结构件,例如在航空航天上的固定设备,电子电器上的定位设备,同时在自动化生产中,许多机械零件都是由6061铝合金材料制造。粉末冶金已经有很久的历史,最早可以从上世纪40年代说起。它与传统铸造法相比,除了环保节能、接近净成型等优势,还可以有效避免成分偏析,确保合金具有均匀稳定的性能。粉末冶金是用金属粉末或金属粉末与非金属粉末的混合物作为原材料,通过成形和烧结来制造出金属材料、复合材料以及各种类型制品的工艺过程[1]。粉末成型应用广泛,成型精密,因为粉末成型得到的制件已经很接近所需要产品的要求,故能很大程度上减少了后期的加工,节约了能源和材料,实现环保的同时有高效益。利用传统铸造方法与机械加工方法无法制备的材料和难以加工出的零件,它却可以简单解决,而且能够实现大批量的生产,令工业届很受重视。其不仅应用于计算机行业,还在汽车、能源、生物以及军事等领域广泛涉及,有广阔的发展前景。粉末冶金的成形方法(即粉末压制)有许多种,有钢模成形、等静压成形、连续成形、注射成形以及高能成形等,其中钢模成形法,又称模压法在工业生产中备受关注,应用广泛。模压法是先将粉末放进钢模内,通过模冲对粉末单向或双向加压使其致密成型。因此本课题重点研究6061铝合金粉末压制行为,通过模压、径向压缩(巴西圆盘)以及单轴压缩实验建立6061铝合金粉末压制Drucker-Prager Cap (DPC)本构方程,得到相关材料参数与相对密度的变化规律建立铝合金粉末压制本构方程以及得到材料弹性参数和摩擦系数变化规律,对研究其粉末压制成形规律、优化模具及工艺参数设计具有重要意义。
1.2 粉末成形的研究现状
当把金属粉末内每一颗颗粒都当作致密体时,用传统的塑性力学可以说明金属粉末的变形行为。但是因为金属粉末是由大量颗粒构成的,其中必定和产生一定的微小孔隙,因此它是一个非连续体。连续体的变形是非常复杂的,如果要清楚知道它的整体变形的话,不仅要从每个颗粒的变形情况来入手研究,而且还要根据颗粒间相互的协调关系来研究,也就是用非连续性的介质力学理论来解决塑性变形和塑性致密问题。但是到目前为止,非连续介质力学的基本理论还缺乏一定的研究,对它的理论说明还不是非常的完善,所以现在我们要研究粉末体塑性理论,先把粉末体当作是一个可以压缩的连续体来研究,同时遵循体积不变原则和质量不变定律[2]。粉末材料和致密材料相同,它们的塑性理论都是以屈服准则作为理论的中心要点,屈服准则对粉末的成型来说,是一个非常重要的条件。如果要求粉末对于不同的应力状态,变形体内某点可以进入到塑性状态,同时保持其塑性状态不断进行,那么就必须遵守这一重要的条件。对粉末成型进行研究时,我们一般采用广义的塑性力学模型,也叫作土塑性力学模型。因为土体与粉末材料有极其相似的地方,就是在它们发生屈服时,它们的体积是可以变化的,因此利用土塑性力学理论来建立粉末材料压制成形的模型是可行的。
在土塑性力学方面,Coulomb是最早在这方面进行研究的科学家,同时他也在这方面取得了一定的成就。在1773年,Coulomb基于他的研究提出了Coulomb屈服准则和连续体极限平衡的概念[3]。在1952年,Drucker 和 Prager也对材料的屈服准则进行了研究探讨,在前人Mohr-Coulomb屈服准则的基础上扩充了屈服准则,提出一个新的屈服准则模型[4]。该模型在主应力空间中表现的是一个圆锥面,另外在子午面和π平面上,形状是一个米塞斯圆。可是Drucker 和 Prager提出的这个模型有它还没完善的地方,就是金属粉末的压制所需的压力远远比土力学中的压力要大,如果应用上述屈服准则进行研究,金属粉末会出现体积增大的情况,这是与现实不符的。所以在1957年时一个新的模型——弹塑性材料硬化模型再一次让Drucker等人提出,就是在Drucker-Prager 圆锥面的基础上加上了一个椭圆帽,将屈服准则模型更好地完善了[5]。另外Sandler和Rubin在实验中,发现压缩角会在实验时变软,由此他在这个现象的引导下,在他们的《CAP模型的算法和模块化子程序》一文中提出了一种修正的硬化规律算法子程序,来防止发生变软的状况[6]。同时Gu 和 Kim等创建了帽子模型,材料为MH-100铁粉,它的模型参数也通过相关实验得到验证,同时对该模型做了大量的应变模拟和变形模拟,得到的载荷-位移曲线与压坯件密度变化与实验数据基本一致[7]。很好地验证了模型的预测能力。Rahman 和 Ariffin加入了温度这个因素,考虑了温度对材料产生的影响,在帽子模型的基础上提出了热力耦合模型。




