金属玻璃结晶诱导剪切模量变化与热量释放之间的关系

国立师范大学物理系 列宁街86号 沃罗涅日，俄罗斯，394043

学院固体物理RAS，莫斯科区，切尔诺戈洛夫卡，142432，俄罗斯

物理研究所，中国科学院，北京，100190

文章信息

文章历史 收于2016年4月2日 修订时间2016年5月11日 接收于2016年6月1日 登网2016年6月10日

关键词：金属玻璃，结晶，剪切模量，缺陷

摘要：众所周知，金属玻璃的结晶伴随着强烈的热释放。目前的文献认为这种现象在一般意义上是因结构排序和相关过程焓变降低造成的。对于结晶诱导的热释放的唯一具体解释是在最近的间隙原理理论和弹性偶极子模型的基础上提出的。这次工作所展现的热释放的测量和剪切模量的变化是发生在一系列Zr和Pd基的金属玻璃的结晶上的。所进行的试验分析进一步明确支持了热释放是由于间隙原子的失去造成的，与在玻璃熔体中的熔体“缺陷”（弹性偶极子）冻结及其弹性能量的耗散类似。整体分析认为，结晶时剪切模量的变化控制了热释放，从而构成这些量之间的普遍关系。

1. 介绍

一般经验认为金属玻璃的热处理（MGS），以及所有其他玻璃，都会导致不同的热效应。前两种热效应是由玻璃态的结构驰豫决定的，这定义了1）热释放低于玻璃化的转变为温度T_g2）热吸收高于过冷液态Tg，第三种热效应是以玻璃结晶为条件，导致的一种强烈的热释放。第三种热效应的绝对数值远大于前两种。

与此同时，这三种热效应的物理性质至今仍不清楚，并且构成了一个广泛的争辩话题。对于先前提到的1）和2）的热效应的起源，一个很受欢迎的概念是由van den Beukel和SIetama提出的，他们认为玻璃态的热效应取决于“自由体积”的总数，这导致无论是热释放还是热吸收都根据于驰豫动力学来解释。这个概念，一方面有后续的调查支持，但是，另一方面，被多方面所批判。

另一个在MGS中的热效应是由最近的文献所提出的。这个理论认为热释放/吸收低于或接近结构松弛的Tg，这可以被退火/结构生成单元（缺陷）类似于简单金属中的哑铃（分裂）缺陷所解释。这个想法是建立在间隙原理理论上的，该理论认为简单金属的熔化是通过间隙原子的快速生成而形成的。这些热效应是建立在基本单原子晶体结构上的以及它们被文献重复引用的在熔化过程中的重要作用。最近在铝单晶体上的实验为这种熔化机制提供了强有力的支持，这与间隙原理理论的预测很吻合。这些“效应”在液态保留着他们自己的个性，而且再通过计算机对液态和玻璃态的多次模拟中，这些效应可以被称为“线弦”。据说这些线弦与间隙原子在晶体中的特征相类似。此外，间隙原子的线弦描述被间隙原子理论的原始版本采纳。这个概念液态有少许间隙原子“缺陷”推动了平衡态和过冷态的液体的特定性质的成功解释。

熔融淬火冻结了一部分这些“缺陷”在固态玻璃中。这可以假设他们和母体晶体状态保持了相同的基本性能特点。事实上，非晶铜的分子动力学模拟表明这种结构包含了纳米大小的区域，这里有特定的内部应变场和低频振动模式，这完全与Cu晶体的间隙原子所创造的相同，虽然这些区域不能被认定为确定的拓扑元素。在MGS中的一些松弛现象成功描述了假定的热处理导致的类间隙原子浓度“缺陷”冻在金属中的变化（综述，参见文献[33]）.特别的是，任何“缺陷”浓度的变化导致“缺陷”形成焓的释放/吸收，这推动先前提到的热效应是可以被系统阐述的。这表明并证实了这种方法解释了在MGS结晶过程的热释放并且更多的是提供了一个关于结晶放热动力学的深刻精确的解释。这意味着在结构弛豫和晶化的MGS发生热影响的性质是通过间隙原子“缺陷”相关的弹性能量，消耗热量在结构弛豫（Tg以下）和结晶。在玻璃化转变温度区域，间隙原子总量“缺陷”的数量增加导致了热吸收。

另一方面，分裂原子代表一个点对称的局部原子模型的“弹性偶极子”的特定情况，这低于周围的材料的点对称性。认为弹性偶极子与施加的应力相互作用并限定一定量的冷冻弹性能量。 它们的浓度或能量的任何变化（例如，由于相互取向的改变）然后导致放热或吸热。这个框架概念是最近基于非线性弹性宏观理论发展来的。这给予热效应和间隙原子理论很相似的分析表达式，尽管他们的出发点完全不同。

在这项工作中，我们测量了基于一些Zr和Pd基的MGS的结晶热，并将他们和利用间隙原子理论和弹性偶极子模型所计算出来的内部能量所比较。这些量之间有一个很好的对应关系。得到的结果对于理解结晶诱导热释放弹性能量的耗散与间隙原子理论“缺陷”和玻璃熔体产生的冻结的弹性偶极子给予了强有力的支持。由间隙原子理论和弹性偶极子的模型表明，结晶热释放是由玻璃和母体晶体剪切模量所控制，这可验证所有在调查研究中的MGS，一些可以区分这些量之间的通用关系。

1. 实验

玻璃态的Zr56Co28Al16, Zr55Co25Al20, Zr46Cu45Al7Ti2, Zr65Al10- Ni10Cu15, Pd40Cu30Ni10P20, Pd41.25Cu41.25P17.5 and Pd40Ni40P20（百分比）有熔体吸附（Zr基的MGs）和熔喷法（Pd基的MGs）被选为这次调查实验的研究对象。所有的玻璃态通过X射线衍射保证是完整定型的。差示扫描量热法是利用日立exstar DSC 7020仪器在Ar气氛中进行。室温下的GRT的MGS的初始剪切模量由参考文献【40-44】得知。剪切模量的温度依赖性是由电磁声变换方法测得的，采用5*5*2立方毫米的样品振动共振，根据G=Grt*f^2/f0^2, 频率为f =500-600kHz（忽略密度变化为1%），其中f0是初始的室温横向振动频率。相对误差取决于G/Grt，增加了10ppm，接近于室温的100ppm,接近于Tg,

在0.013Pa真空中测得的剪切模量。

1. 结果

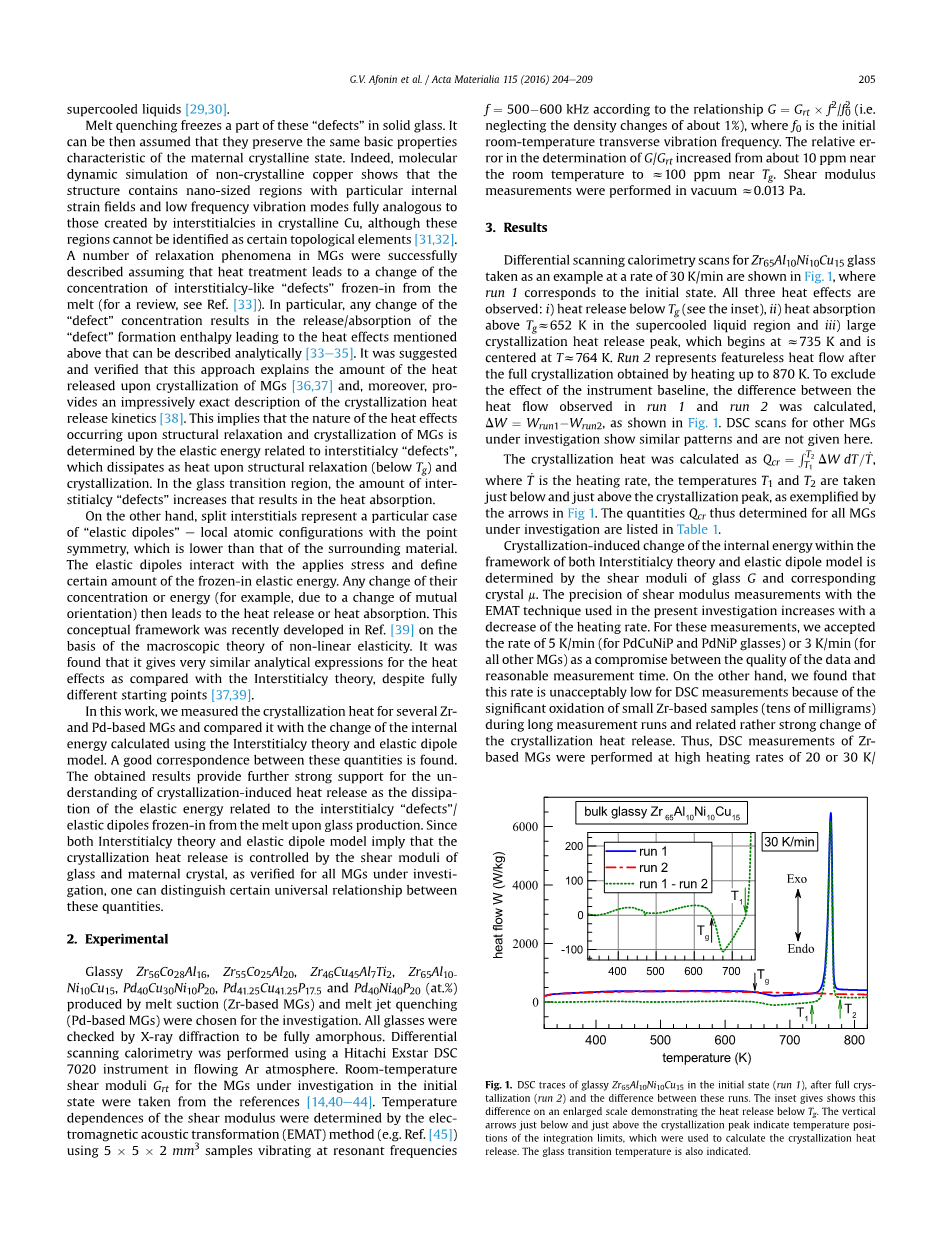
差示扫描量热法Zr65Al10Ni10Cu15玻璃态为例的速度在30 K / min的如图1所示，其中运行线条图示1对应于初始状态。所有的三个热效应可以被观察到：1）热释放低于Tg（见插图）2）过冷液体区域的热吸收高于Tg = 652 K，3）大量结晶放热峰，开始在 735 K，并集中在T = 764 K。线条图示2表示了在加热到870k的全结晶后得到的普通热流量。排除仪器基线的影响，热流量的差值可以通过线条1和线条2计算得到，Delta;W=W_run1-W_run2,如图一所示，

DSC扫描其他的在研究调查下的MGS与此有相同的模式，这里就不给出了。

结晶温度由公式Qcr=.,这里的T.是加热速率，温度T1和T2是在结晶峰的正下面和正上方，如图1中的箭头。所有研究对象的MGS测得的Qcr 的量列在表一中。

间隙原子理论和弹性偶极子模型的结晶诱导的内部能量的变化是由玻璃的弹性模量G和对应晶体mu;决定的。剪切模量的精确度测量是由EMAT技术通过在现有调查中增加一个逐渐减小的速率来测得的。对于这些测试，我们接受5 K / min的速率（PdCuNiP和PdNiP玻璃态）或3 K / min（所有其他MGS）作为数据的质量和合理的测量时间之间的折衷。另一方面，我们发现用DSC测量的速率低的无法测出，因为小Zr基样品在长测量时间内和相关的结晶热释放中显著氧化。因此，对于Zr基的DSC测量是在20或30K/min的高加热速率下测得的。对于Pd基，氧化不是那么明显，因此，在DSC中的加热速率为3或5K/min也是可以的。

图示1.玻璃态的Zr65Al10Ni10Cu15初始状态见曲线1，经过充分结晶（曲线2）以及这两条曲线的差距。插图展示了在扩大规模下热释放低于Tg的差值。结晶峰的下上方的垂直箭头表示的是温度的位置和积分限制。玻璃化转变温度也表示如此。

表一.研究对象的MGS的参数：密度为rho;，析晶热Qcr,结晶前的弹性模量G，结晶后的弹性模量mu;，剪切磁化系数beta;i,（间隙原子理论），剪切磁化系数beta;ed（弹性偶极子理论），浓度缺陷c,晶化退火，每种缺陷的结晶热Q_CR^d，每种缺陷的结构驰豫热Q_SR^D,间隙原子生成焓H_i。

图二展示了典型的玻璃态的Zr基和温度相关性的剪切模量。结构松弛曲线G（上面的虚线），玻璃化转变温度迅速降低（如箭头所示）。结晶开始于Tcr=706K，在G=27.0GPa，T=T_cr，mu;=37.6GPa,稍高于Tcr, 剪切模量开始急速上升，结晶诱导剪切模量变化，因此，Delta;G_cr=mu;-G=10.6GPa,如图2。这是剪切模量G和mu;决定的如上所述的结晶热Qcr, 这是现有研究的兴趣点所在。其他所有玻璃态的Zr基的剪切模量揭示了相同的模式。表一所示的是结晶前的剪切模量G 和结晶后的剪切模量mu;。

Pd基在研究中显示和Zr 基的MGS 相比有更大的粘弹性。在这种情况下，使用EMAT技术所测量的剪切模量可能达到Tg 20K的温度，在这个温度下，由于温度内耗的快速增大而导致共振曲线的快速展宽，同时其高度的急剧下降，使得测量系统无法自动跟踪谐振频率。测量信号丢失后，加热仍然持续到660K，便可得到完全结晶结构。待冷却到室温后，对结晶样品进行第二次测量。然后，结晶诱导的剪切模量变化Delta;G_cr=mu;-G，估计在结晶起始温度TCR（由DSC测定在相同的加热速率）和在相同温度下的玻璃的外推剪切模量G和结晶样品的剪切模量mu;之间的差异，如图3所示。基于Pd基的G和mu;的数值在表一给出。

1. 讨论

4.1理论背景

让我们比较一下获得的结晶热Qcr和剪切模量变化Delta;Gcr的数值和间隙原子理论和弹性偶极子模型的预测值。

忽略在结晶过程中的密度变化，初始玻璃晶态每个单元体积的内部能量和参考晶体的差值rho;Delta;U是可以用间隙原子理论计算出来的，（1），这里的rho;是密度，G和mu;是分别是玻璃态和初始晶态的剪切模量，beta;_i是无量纲磁化系数，用定义，ε是切应变。beta;_i这个定义表明，这个数量反映了原子相互作用势的非谐性。而剪切磁化系数是可以通过比较玻璃态实验热流量和间隙原子理论中计算出来的热流量来比较。 （2）这里的G和mu;分别是玻璃态和参考晶体的温度相关剪切模量。beta;_i作为一个拟合系数，人们发现，这个方程W(T)很好的描述了玻璃态和结晶态实验热流量。所有的beta;_i均可从文献中获得，并且在这项工作中导出的四舍五入为整数的值记录在表一中。可以观察到，不同的玻璃态的剪切磁化率是相差不大，平均为。特定的beta;_i估测误差在6-7%。

弹性偶极子模型认为，内部能量的变化可以表述为内部应变膨胀，通过玻璃态生产中冻结的弹性偶极子产生。修改后的模型中玻璃晶的转变产生的内部能量的变化可由下面公式获得：（3），这里的Omega;_t=1.38是一个平均形式因素，这考虑到了结构中不同的弹性偶极子类型和剪切磁化系数beta;_ed定义为，这里的Upsilon;4是拉梅弹性行数的四次方。就如在间隙原子理论中的剪切磁化系数beta;_i一样，beta;_ed在方程中是由原子间相互作用势的非谐性测定的。可以看出，公式（1）和（3）的内部能量的变化，通过间隙原子理论和弹性偶极子模型计算的是比较接近但不完全相同，特别的，他们的剪切变化率是不同的即beta;_edne;beta;_i。

修改后的弹性偶极子模型框架的热流量由下列公式给出，（4），表达式中的剪切磁化系数beta;_i和beta;_ed分别有公式（2）和（4）给出，他们的关系如下：（5）。把关系式（5）到表达式（3）中，最后找到由弹性偶极子模型给出的内能变化：（6）。这个公式可以直接的由间隙原子理论推出的内部能量变化（1）相比较。

玻璃晶化时发生的体积变化对内能的变化贡献不大。然后，每单元体积的玻璃态和参考结晶状态的内部能量变化rho;Delta;U的差值由方程式（1）和（6）给出，这应该被视为单位体积结晶热。即rho;Delta;U=rho;Qcr。这个方程可用来作为结晶热和结晶时剪切模量变化的比较。

4.2实验对比

首先，相对误差的量的确定rho;Qcr和rho;Delta;U应该被估测出。我们所能接受的密度和结晶热的误差分别在2%和5%，以至rho;Qcr误差大约为7%。由间隙原子理论框架推导出的内部能量变化的相对误差（方程式1）由给出。对于Zr基来说，，，对于晶态 Zr56Co28Al16，。对于Pd基来说，d G /G . d mu;/mu;，由于上述的外推过程（图3），结晶温度附近的误差明显较大。我们估计这个误差大概在2%而且这个估测值是可以被接受的。弹性偶极子模型（方程3）对于相对误差给出了更为复杂的表达，这里省略了。 d G /G . d mu;/mu;（不同于Zr基和Pd基）和Omega;t同样给出，同时d beta;_ed/beta;_ed=1/17，这个表达式对于d rho;Delta;U/rho;Delta;U也有相同的相对误差。

图4显示了由（1）（6计算的）结晶诱导改变的内部单位体积的能量，作为调查研究中的所有玻璃态单位体积的rho;Delta;U和函数表达式。如上所述的相应的误差条，可以看出，间隙原子理论和弹性偶极子模型给出的内部能量变化的值非常接近于玻璃态结晶内部能量的变化值。这证实了早期的结论，不同的弹性和热现象，这些方法给出了非常相似的结果。同时也注意到，剪切磁化系数beta;_i和beta;ed 在间隙原子理论和弹性偶极子模型中的差别小于10-15%，详见表1.

图四还显示了通过原点绘制的统一斜率直线。很明显的看出，这条线提供了一个很好的近似rho;Delta;U 的数据集。通过所有数据点和原点，用最小二乘法绘制出了同样的斜率线。可以得出结论，通

全文共7504字，剩余内容已隐藏，支付完成后下载完整资料

英语原文共 6 页，剩余内容已隐藏，支付完成后下载完整资料

资料编号：[143924]，资料为PDF文档或Word文档，PDF文档可免费转换为Word