英语原文共 7 页，剩余内容已隐藏，支付完成后下载完整资料

有机物封装微纳光纤谐振腔

【摘要】文章提出了一种制作微型光学电路，并用一种低折射率的有机物封装微纳光纤的简单方法。这里论述的例子为采用含氟丙烯酸甲酯的微型硅纤维环形谐振腔。在文中，我们对其的制备问题以及初步的实验结果进行了介绍，并对认识Q值的目前局限，封装的低折射率有机物在未来谐振器的Q值中所扮演的角色进行模拟。预计通过这项技术，我们使用市售的聚合物制造出半径为100mu;m的高Q值谐振腔。

关键词：光谐振器 集成光路 微米光纤 纳米线

1. 导言

光学谐振器一直是众多光谱仪等光学器件如过滤器,延迟,或激光等中的一块基本构件。同电子器件的发展趋势相同，尽管现在处于一个比较成熟的阶段，光电学仍向着小型化和集成的方向发展。这带来了许多挑战和机遇。尤其的，许多基于微谐振器的新设备和功能最近被提出或证实。举几个例子，包括调节器[1]、开关[2],[3]、激光[4]、生物传感器[5]和类似电磁诱导透明效应[6]。目前人们正在探索几种技术使光学微电路得以实现化。比如在玻璃[7]、聚合物[8]、半导体[9]、玻璃微珠上光刻写电路[10]，基于表面等离子体共振金属电路[11]，光子晶体[12]，微纳米线半导体[13]或玻璃[14]。

自从被发现[14]，玻璃微纳光纤谐振器凭借其独特的低损耗，易于制备的特点得到了人们的密切关注。到目前为止，这种谐振器被证实只能存在于空气或水中[15]，或者是加入气凝胶[16]、MgF2[15]的低折射率的物质中。本文旨在说明微米光纤谐振器也可以存在于固态基质中。文章首先论述空气中的微米光纤谐振腔，然后说明有机物封装微米光纤谐振腔最初示范，最后讨论谐振器的发展潜力和模拟条件。

1. 空气中的微型谐振腔

微纳光纤谐振器是光学纤维谐振器的微型版本[17]，但微米光纤谐振器的结构更为简单，因为微纳光纤中由于衍射产生的大消逝场通过横向的联系具有非常高效的耦合效应。实际上，通过折叠微型纤维本身，我们可以得到一个微米光纤环。实验室条件下，由于静电力和范德华力的存在，通过折叠微纳光纤得到的微米光纤环能够得以保持。

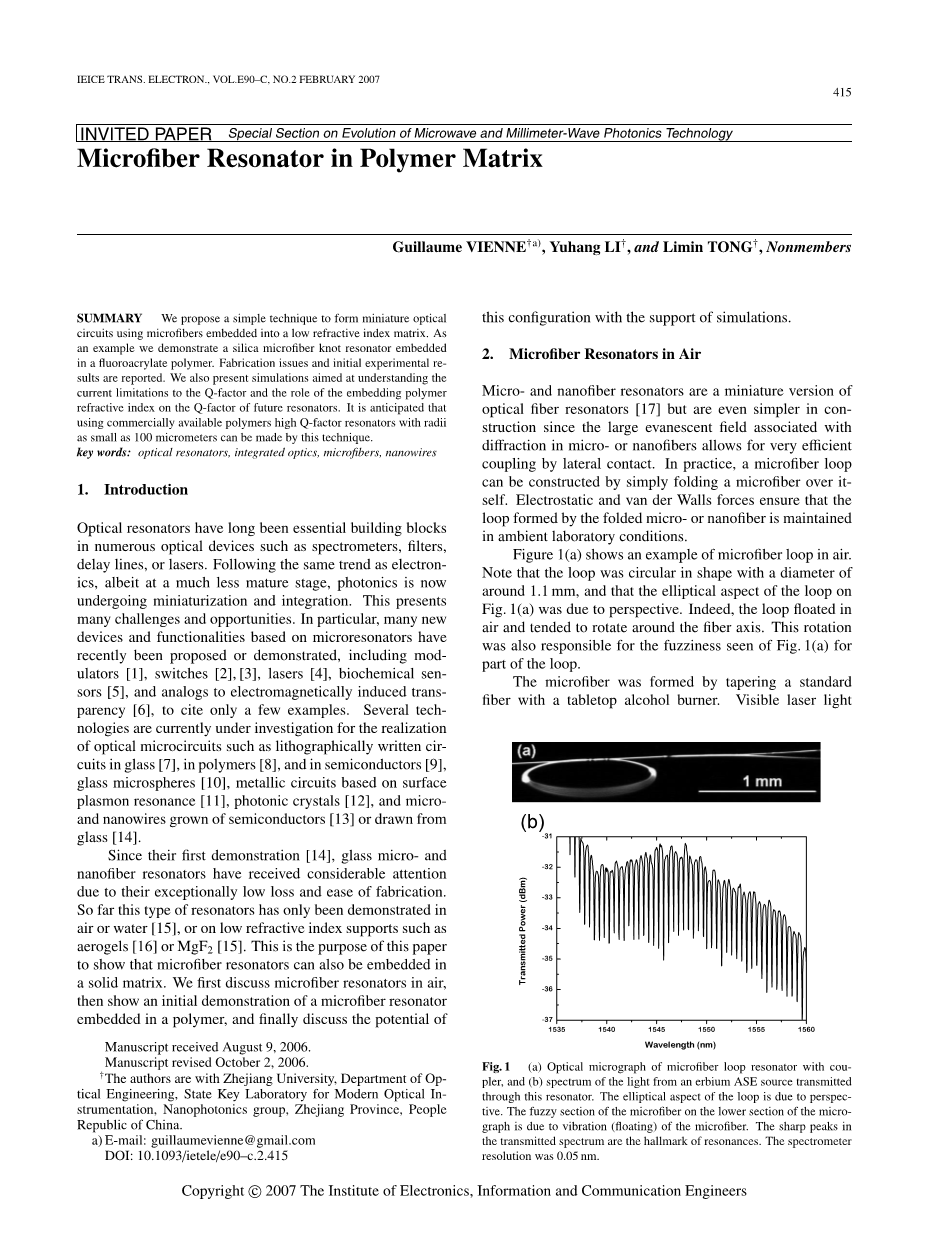
图片1(a)为空气中得到的微米光纤环。我们注意到这个环的形状为直径1.1mm左右的圆形，由于视觉影响，它看起来像是椭圆。事实上，微米光纤环可以悬浮在空气中并且有围绕着光纤轴旋转的趋势。图1(a)中光纤环的一部分看起来比较模糊，因而我们所说的这种旋转的存在是可靠的。

图1

(a)为微型纤维耦合谐振腔的光学显微图像,(b)光源为铒ASE的谐振腔透射光谱。纤维环椭圆的形状是由于角度造成的。显微图片下方微型纤维模糊的部分是由微型纤维的振动造成的。透射光谱中尖锐的峰是谐振器存在的标志。光谱仪的分辨率为0.05nm.

在桌面酒精灯灼烧下逐渐拉伸标准光纤，我们可以得到微米光纤。由于可见激光发射锥使得微型显微可视化，于是我们可以在光学显微镜下对纤维进行打结。我们将末端附有涂层的纤维放置在显微镜载玻片上，然后用两个平行的裸露的显微支撑微型纤维。这两根纤维不会阻碍我们的操作，却可以抑制微型纤维的悬浮。一个纤维环可以通过手动操作两个显微操纵器，包括用手柄逐步拉伸纤维得到。使用显微操纵器控制微型纤维的末端，使其先打成一个环形。然后将纤维的自由末端穿过这个环形成一个结。最初结的直径大约为1cm。将微型纤维的自由端和放置在显微操纵器上的锥形纤维粘合在一起，这样显微结会变紧，从而能够达到预期的直径。图1中展示的显微结直径大约为1.1mm,构成这个节的微型纤维的直径大约为3.3mu;m。铒ASE光源发出的光在通过尖锥发射进入微米纤维环。微型纤维的两端被支撑着，放置并与耦合装置中另一个锥形的标准光纤相接（如图1的右侧(a)），收集透射光并将其导入光学光谱分析仪（ANDO AQ6315）。透射光谱如图1中(b)所示。光谱的总体变化遵循ASE光源光谱，而梳状结构是由谐振产生。谐振峰位的等距间隔，即自由平普范围是0.5nm。在波长范围内谐振峰的半高宽是衡量Q值的一个因素，即谐振腔储存能量的能力。近期，Sumetsky et al.发现一种可以承载高达120000Q值的微型谐振器[18]。最近，我们也报道发现了一种可用来代替微米纤维环的微型纤维结，它是一个错综复杂的区域而不是一个简单重叠的部分，具有耦合效应。这种纤维结比微米纤维环更加稳定，并且具有类似的性能[15]。直径在几毫米到几十微米范围内的微型谐振器已经被证实可以由直径在几微米到几十纳米范围内的光纤制备得到。微纳米谐振器发展前景是具备较高Q值以及通过其极大地消逝场实现超灵敏感应[18]。

1. 聚合物中的微型谐振腔

微纳光纤谐振腔处于空气介质下的主要缺点是它对环境扰动的极度敏感性，哪怕是风或者周围的灰尘。空气中的微纳光纤的浮动可以通过支撑物减轻，但即使在有支撑物的情况下，它的机械稳定性依然很差。此外，来自灰尘的污染也是一个问题。将微纳米光纤环封装在固态基质中有利于它在实验室以外环境中的实际应用。

为了保证光在微米光纤中的传播方向，周围的物质应当比光纤具有更低的折射率。到目前为止最常见的光学纤维材料是Si,它具有相对较低1.44—1.55的折射率。氟化玻璃和聚合物具有更低的折射率，因此适合做包层材料。本文中，我们所选的纤维材料为Si,包层材料为一种紫外光固化氟聚合物EFIRON PC-373[19]。

从显微镜载玻片上剪取一小片玻璃，涂覆上一层EFIRON PC-373，接着在汞灯下照射10s(Mejiro Genossen MUA_165在365nm处可传递3800mW/cm²的能量)。一根标准的光纤可拉伸为直径5mu;m的微米光纤。将微米光纤在空气中打结的具体过程在第二部分有描述。接着，将光纤结用聚合物基质进行固定，并用一滴EFIRON PC-373封装，再经过一秒的紫外固化处理。最终微型纤维谐振腔就可以被完全的封装在坚硬的聚合物中，得到很好的保护。需要注意的是，环形结构并不适用这个过程，当纤维被侵入在水中时，在力的作用下微型纤维相邻的部分相互吸引，耦合区域在很大程度上被削弱，使得环不能够保持。图2(b)所示的绞合部分是获得谐振器必不可少的结构。我们尝试比较空气与有机物封装两种条件下谐振器的特性，却得不到一致的结果。造成这种错误的主要原因可能来自耦合器输出时用于谐振腔传输到光学光谱分析仪能量的不稳定性。

图2 光学微米光纤中的谐振腔结构

(a) 氟化丙烯酸酯封装微型硅光纤谐振腔。频率为ND:YAG激光2倍的绿光传入微米光纤。(b)谐振腔中变焦耦合器(绞合区域)。光纤结直径为1.15mm。微型纤维直径5mu;m。

实际上，包覆有聚合物的谐振器的输出耦合发生了移动，它的传输也因此改变。这个问题说明了空气条件下微型纤维结构的不稳定性，并促使我们的研究向耦合的方向扩展。在下文中我们想要阐明文章推崇的有机物封装微米光纤谐振器确实具有我们想要的功能。

图3是铒ASE光源发射的光在图2所示有机物封装微米光纤谐振器的光谱图。在1450-1650nm的波长范围内我们可以观察到谐振现象，尽管当前的实验设备，1480nm以下的和1620以上的噪音使得实验现象很模糊。根据图4我们可以进一步分析实验结果。

图3

铒ASE光源发射的光在图2所示有机物封装微米光纤谐振器的光谱图。光谱仪分辨率为0.05nm。局部放大图集中在1500、1550、1600nm附近。

图4为自由光谱范围对应的波长，它们的计算可以根据下面这个公式：

其中 是波长； 是谐振腔的直径， 是谐振器材料的折射率， 是折射率随波长的变化率。 取1.15mm(测量值)。折射率和硅的色散来自于参考文献[20]。方程可以解释材料的色散但不能解释波导色散。我们也可以在忽略色散的条件下将计算值化成比方程1更简单的形式。

由于色散只有轻微的影响，因此这个简化的方程足以和测量结果吻合。

图4说明了谐振的消失比对应的波长的关系。

图4

(a)自由光程范围 (b)消失比 (c)图3光谱分析中Q值对应的波长 图(a)也绘制了由方程1、2计算得到FSR值。

消失比在整个可测量范围内高于6分贝。在1560nm附近的峰值接近10dB.曲线的确切形状有待分析，而峰可能是由于位于中心1560nm处的聚合物透射窗口造成的。图4说明了在整个波长范围内Q值的微小变化。Q值在11000到14000范围内变化。尽管这里的实验结果是仍是初步的，但令人鼓舞的是，我们看到这些值只比空气中的最优良的微型纤维谐振腔的Q值低一个数量级（见sect2）。在sect4中，我们将对于Q值进一步讨论。

可以发现谐振峰随着UV固化后发生了改变，但很快就保持稳定（在3分钟之内）。我们发现当UV光源照在树脂上，不论其是否已经聚合，总会引起谐振峰值波长的转变。造成这种UV转变的原因在这里并没有阐明清楚，可能是由于在紫外光的照射下聚合物的折射率发生了改变。这样一个有趣的效应并没有什么实际意义，但我们应该记住的是UV固化后，至少等待几分钟再测量谱的稳定值是十分必要的。

而在空气中，未封装的谐振腔的性能很快退化主要是由于微型纤维表面沉积了灰尘。为了证明聚合物封装技术可以保证稳定性，我们每隔24小时通过聚合物封装谐振器测试透射光谱。结果如图5所示。可以看到再次期间光光谱只发生了轻微的变化。我们观察到的主要差异是在24小时后谐振光谱-0.025的漂移。造成漂移的也许是由于测量不准确，因为这低于光谱分析仪的分辨率，即0.05nm。在领域的应用还需要更长期成熟的研究。

图5

图2所示有机物封装谐振腔经过1h、25hUV固化的谐振谱。图中也包含经过25hUV曝光，漂移 0.025nm的光谱。

1. 拟合及讨论

在这个部分我们将要解决上述有潜力的技术的局限性。

我们首先在图6中阐释了第三部分的实验结果。

根据参考文献[21]，结的透光率可以建立以下的方程式：

其中 是相位因子，即 （这里引入一个相位 ）， ， 分别代表耦合损失、电耦合系数和一个循环的总振幅损失（同参考文献[21]中的概念一样）。在图6中，对测量光谱和基于方程3的最佳拟合进行了比较。最佳拟合指数即为图中的数字。这次拟合非常接近于测量光谱。从获得参数可以发现我们距临界耦合较远， 与 相等（见参考文献[21]）,消失比达到最大值。这也许可以解释为什么测量的消失比（见图4(b)）相对来说比较低。

根据[22]可以计算出Q值：

这里 是总损失，是

的总和。

图6

图2 中纤维结测量值和发射功率随波长的变化。点划线是实验数据，实线是对方程3的拟合。纤维结的直径D为1.15mm（测量值）。拟合参数即为数字所示。 ， 分别代表耦合损失、电耦合系数和一个循环的总振幅损失（同参考文献[21]中的概念一样）。

这两项通过最佳拟合参数进行计算。Q值根据方程4-方程6计算，为1.21times;10⁴ ，这与由半峰宽（见图4）计算的结果十分吻合。通过将微型纤维打结我们观察到它的光散射增加了。表明这个过程中收到了污染。从这个现象我们可以认为 可以显著下降，因此Q值可以增加。但最有启示意义的是限制Q值的主要因素来自耦合 。确实，电耦合系数为0.249远达不到最佳值。理想情况下，它应该接近于1以确保具有足够的密度来建立空腔。对于一个给定直径的纤维结，耦合器的长度不能随意改变。一方面，耦合强度取决于消逝场的范围，它随着微型纤维直径的减小而增大。低的电耦合系数也许是由于在这次试验中使用的微型纤维直径较大（5mu;m）。以后，我们会使用更细的纤维来制备谐振器来增加电耦合系数。我们注意到有趣的一点，由于相比较下指数降低，当包裹微型纤维谐振腔的包层材料由空气变为聚合物时，消逝场的范围变大了。这也就意味着聚合物封装的谐振器的耦合长度比空气中的耦合部分更短。这对于小纤维结尤其重要，它的缠绕部分非常短。在这种情况下耦合长度需要变短以接近全交叉耦合（K→1）才能得到高的Q值。另一方面把包裹材料由空气变为有机物对吸收和辐射损失没有有利的影响。这是接下来要讨论的课题。

微纳光纤的损失比起波导光刻写或表面等离子体波导要低得多。已经证实损失低至1dbm-1[23]，我们认为基于对纤维显微结构的研究，这个数字还可以进一步减小[24]。这对实现极高Q值的微纳纤维谐振器提供了发展的空间。

下面我们研究了聚合物的存在如何影响微型纤维谐振器的Q值，假设可以实现完美的交叉偶合（忽略K对于Q值的贡献）。包裹材料折射率指数的实部和虚部都发挥作用：折射率指数的实部影响弯曲损耗，而虚部通过消逝场影响吸收损耗。

所有的固体材料的折射率都比空气大（n=1）。包层材料的折射率对于微型化都是一个重要的参数，因为弯曲损耗增加了包层和内芯间的相对折射率。在图7中我们画出了不同包层材料Q值对谐振腔半径的图（我们认为谐振器是圆形）：空气中（n=1），Telon AF2400（n=1.29）[25],EFIRON PC-373(n=1.37)。光学波长可认为是1.55mu;m。弯曲损耗可以根据[26]中导出的解析公式据算得到。我们应该注意是这个公式基于弱逼近，并且结果应该通过充分的计算来进一步修正，它对于推导一般准则仍然有用。

图7

Q值对空气中的超细纤维环（实线），在Teflon中（虚线），在没有损耗的PC 373中（点线），在损

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[147653]，资料为PDF文档或Word文档，PDF文档可免费转换为Word