摘 要

热电材料是一种可以实现热能和电能互相转化的功能材料，因而在温差发电和热电制冷领域有广泛的应用。Bi₂Te₃基热电材料是目前室温下商业化应用最成熟的热电材料，但其热电性能离规模化应用仍有差距。本文通过设计并实现了Ni/Bi_0.5Sb_1.5Te₃(PBT)异质叠层结构，探索Ni层分布在不同方向上对热电结构和性能的影响，从而制得热电性能更加优异的异质叠层结构热电材料。

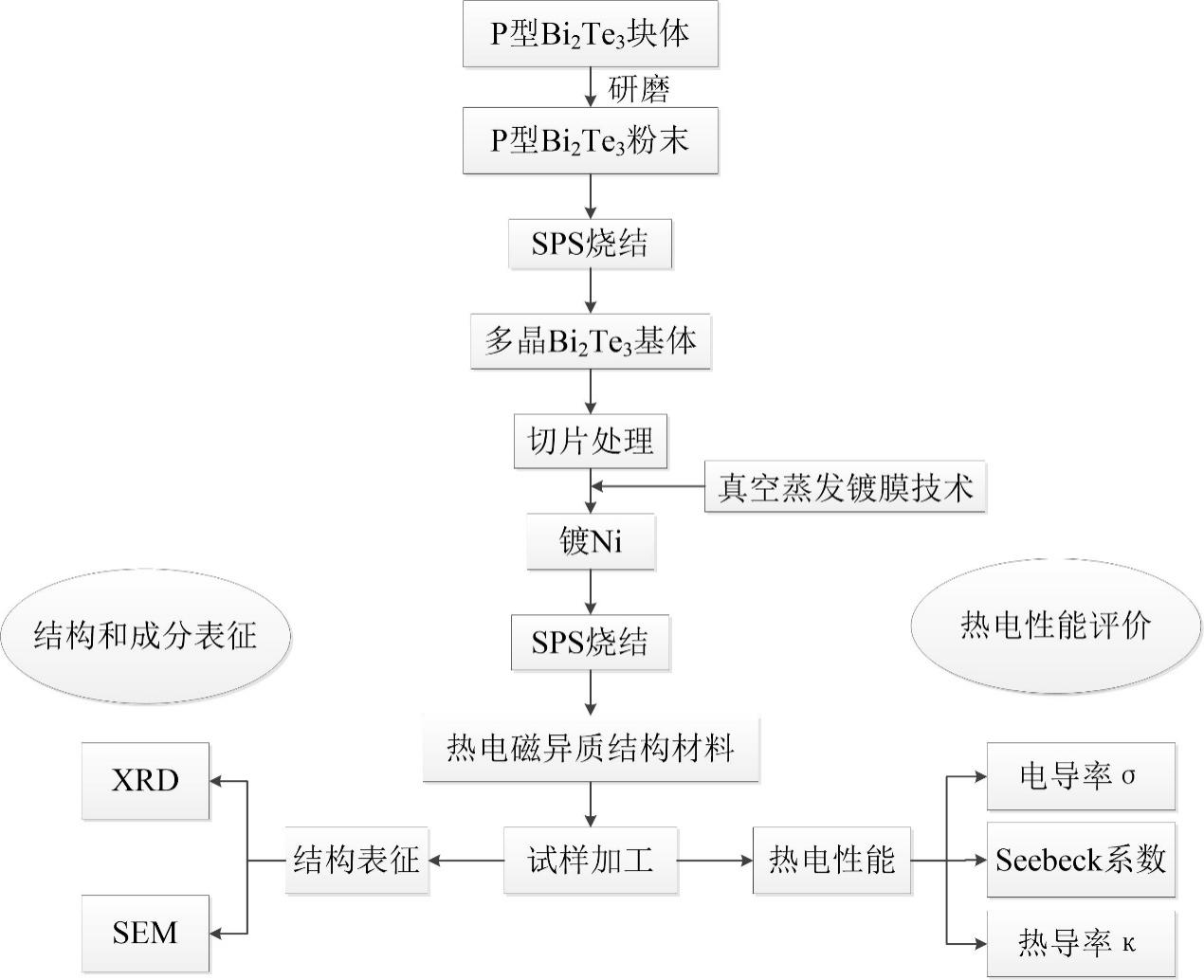
采用真空蒸发镀膜结合放电等离子烧结(SPS)技术制备了Ni/PBT异质叠层结构材料，通过X射线衍射仪(XRD)、场发射扫描电子显微镜(FE-SEM)等测试手段研究了该材料的物相组成、显微结构、化学成分等。XRD分析结果表明：Ni/PBT异质叠层结构材料的主相为P型Bi_0.5Sb_1.5Te₃，同时可能含有第二相Ni或Ni₃Te₂。断面的形貌像、元素点扫描和面扫描分布分析表明：Ni镀层在SPS过程中完整保留，无明显扩散。该异质结构材料在0°方向和30°方向上的电导率、Seebeck系数和功率因子均有所提高，其中0°方向上的功率因子在300K处取得最大值3.61 mW·m^-1·K^-2，较PBT基体材料2.98 mW·m^-1·K^-2，提高了21.4％。而Ni/PBT异质叠层结构材料的热运输性能在90°方向上有大幅度降低，在370K时取得最小值0.84W·m^-1·K^-1, 较PBT基体材料1.20 W·m^-1·K^-1，降低了30％。另外，与PBT基体材料相比，Ni/PBT异质叠层结构材料各方向上的ZT值均有所提高，并在 90°方向上取得最大ZT值0.91，提高了18.7％。

关键词：碲化铋；热电性能；Ni叠层结构；蒸发镀膜

Abstract

Thermoelectric (TE) materials as one kind of functional materials enable direct conversion between thermal and electrical energy, thus providing a wide applications in the fields of power generation and refrigeration. Bi₂Te₃-based materials are the most mature TE materials currently commercialized at room temperature. However, there is still a gap between the TE conversion efficiency and the requirement of  large-scale application. In this paper, Ni/Bi_0.5Sb_1.5Te₃ (PBT) heterogeneous laminated structure has been designed and realized, and the influence of Ni layer in different directions on the structural composition and properties of Ni/ PBT material has been studied.

Ni/PBT heterogeneous laminated structure material were prepared by vacuum evaporation coating combined with spark plasma sintering (SPS) techniques. The phase composition, microstructure and chemical composition were studied by X-ray diffractometer (XRD), field emission scanning electron microscope (FESEM) and other testing methods. The results show that the main phase of Ni/PBT heterogeneous laminated structure materials was P-type Bi_0.5Sb_1.5Te₃, and there may also contain second-phase Ni or Ni₃Te₂. The FESEM of the Ni/PBT heterogeneous laminated structure material shown that Ni layer was completely retained after SPS process without obvious diffusion. The electric conductivity(σ), Seebeck coefficient(α), and power factor(α²σ) of the material in the 0° and 30° direction have improved. The Ni/PBT material in the 0° direction obtained the maximum power factor of 3.61 mW·m^-1·K^-2 at 300K, increased by 21.4% as compared with PBT material which obtained the maximum power factor of 2.98 mW·m^-1·K^-2. The Ni/PBT material in the 90° direction obtained the minimum thermal conductivity of 0.84W·m^-1·K^-1 at 370K, reduced by 30％. At last, TE performance of Ni/PBT heterogeneous laminated structure material have enhancement in all test directions. The maximum ZT value of 0.91 has been obtained in the 90° direction, increased by 18.7% as compare with PBT matrix.

Key Words：Bi₂Te₃; Thermoelectric performence; Ni multilayered structure; Vacuum evaporation

目 录

第1章 绪论 1

1.1 研究背景和意义 1

1.2 热电效应 1

1.2.1 Seebeck效应 1

1.2.2 Peltier效应 2

1.2.3 Thomson效应 2

1.2.4 Kelvin关系 3

1.3 热电材料性能参数 3

1.3.1 Seebeck系数 4

1.3.2 电导率 5

1.3.3 热导率 5

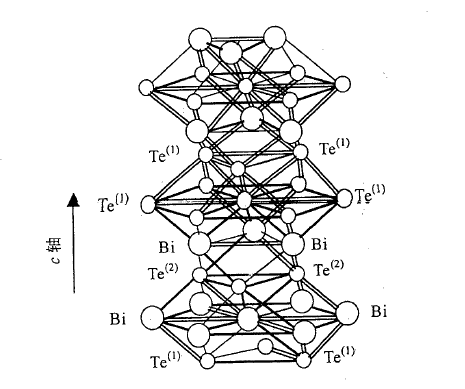
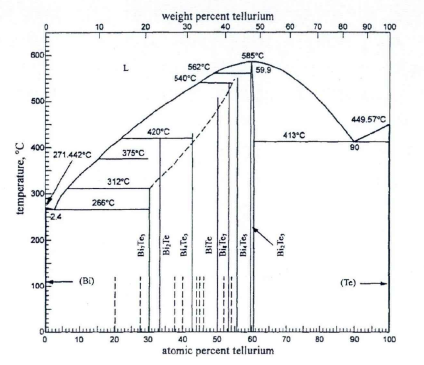
1.4 Bi₂Te₃基热电材料的研究进展 6

1.5 本论文选题意义和主要研究内容 7

第2章 实验方法和实验设备 9

2.1 实验部分 9

2.1.1原料选择与处理 9

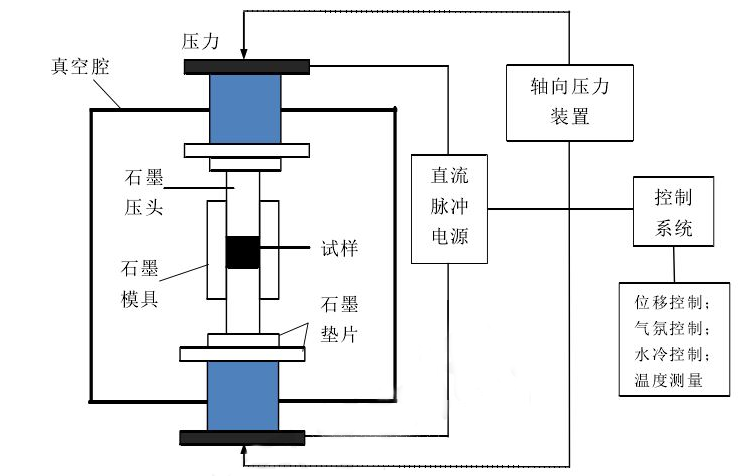
2.1.2 SPS烧结工艺 9

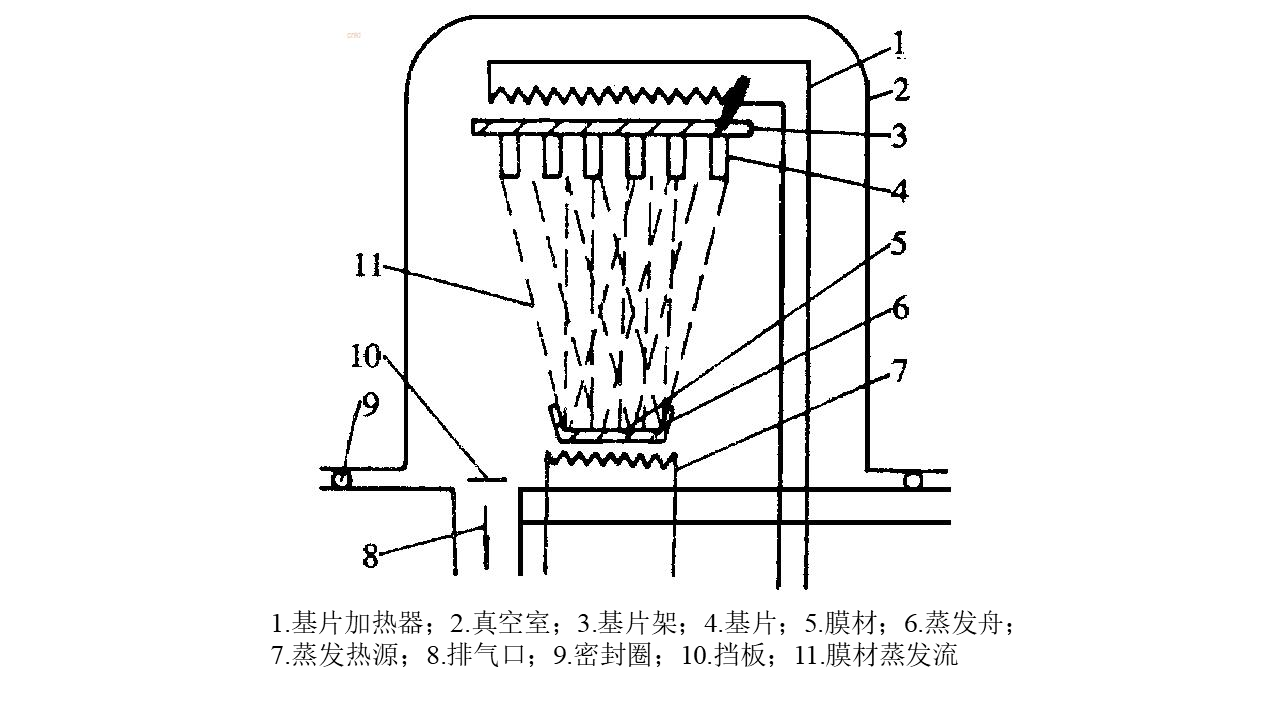
2.1.3 真空蒸发镀膜工艺 10

2.2 样品的表征 11

2.2.1 块体材料密度测量 12

2.2.2 物相组成分析 12

2.2.3 显微结构分析 12

2.3 Ni/PBT异质叠层结构材料的电热输运性能测试 12

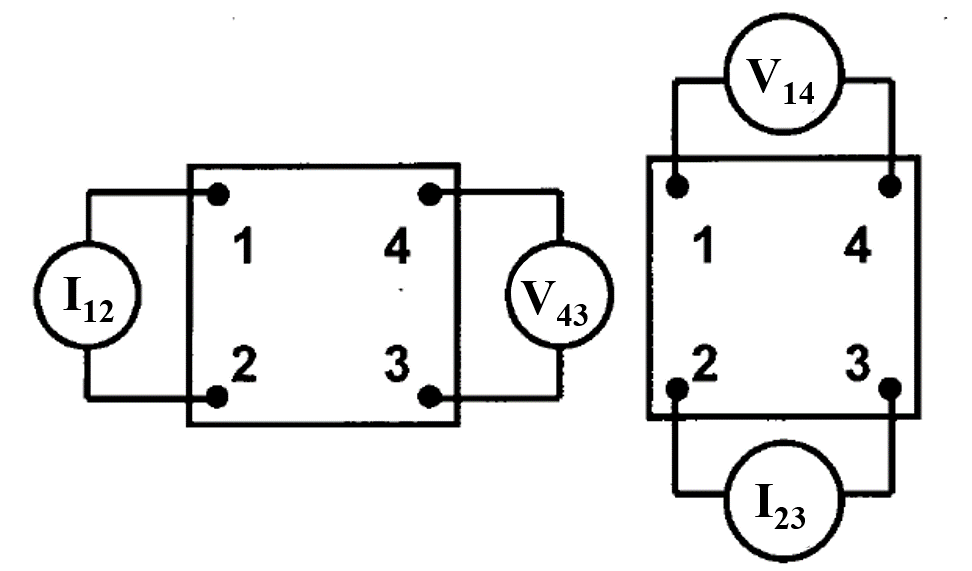
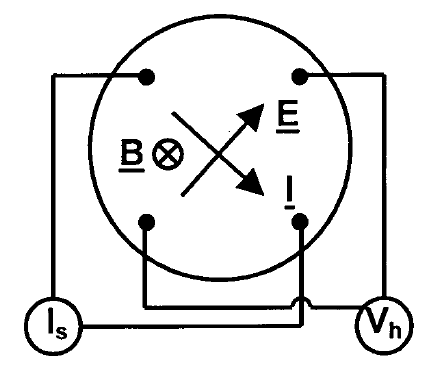
2.3.1 电运输性能测试 12

2.3.2 热运输性能测试 14

第3章 Ni/PBT异质叠层结构材料热电性能的研究 16

3.1 物相组成 16

3.2 显微组成 16

3.3 电运输性能 20

3.4 热运输性能 23

3.5 综合热电性能ZT值 24

第4章 结 论 26

参考文献 27

致 谢 29

第1章 绪论

1.1 研究背景和意义

随着全世界工业化进程和城市化步伐的不断加快，特别是发展中国家的崛起，全世界的能源需求呈现前所未有的增长趋势，煤、石油和天然气等传统能源储备逐渐减少，能源问题已经成为制约国家发展和社会进步的关键因素^[1]。因此，研究和开发合适的新能源和能源转换技术已经成为人们关注的重点。热电材料是一种能将热能和电能相互转换的功能材料，已被认为是新能源材料不可缺少的一部分^{[2, 3]}。

利用热电材料独特的性质，可以制作两种不同的热电装置：温差发电和温差制冷装置^[4]。与传统的发电机和制冷装置相比，热电装置具有结构简单、无污染、噪音小、装置易组装且不易损坏等突出优点^[5]。利用热电材料和热电转换技术可将日常生活和生产中残留的热量用于发电，能够有效解决能源因转换为多余热能而利用率低下的问题。但是目前的热电材料的利用率并不高，主要是因为其热能和电能之间转换的效率不高，无法满足大规模的生产和应用的要求，然而在理论上热电材料的ZT值并无上限，因此如何大幅度提高热电材料的热电性能是目前研究者仍需解决的问题^{[6, 7]}。

1.2 热电效应

1.2.1 Seebeck效应

当不同的两种导体连接成一个闭合回路时，如果两中导体的接触处存在一个温度差，回路中就会有电流通过，并伴有电动势产生，分别称为温差电流和温差电动势，这就是Seebeck效应，由德国科学家Seebeck首先发现^[8,9]。如图1.1所示，两个互不相同导体a和导体b以串联的方式组成一个闭合回路，如果接触处1的温度为T₁，接触处2的温度为T₂且T₁＞T₂，图中y和z之间就会有一个由温差引起的电位差存在，即温差电动势V_yz，其可以表示为：

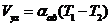(1.1)

当两个接触处的温差△T= T₁ -T₂很小时，系数就为常数，这个常数被称作这两种不同导体的相对Seebeck系数，其表达式如下：

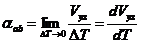(1.2)

Seebeck系数的单位为V·K^-1，式中的温差电动势V_yz可以大于零也可以小于零，这与温度差△T的正负和回路中两种导体本身的性质有关。由此可知Seebeck系数也存在正负之分，若电流的方向与温度降低的方向一致，则Seebeck系数为正，反之为负。一般地，p型半导体的Seebeck系数为正，n型半导体的Seebeck系数为负。

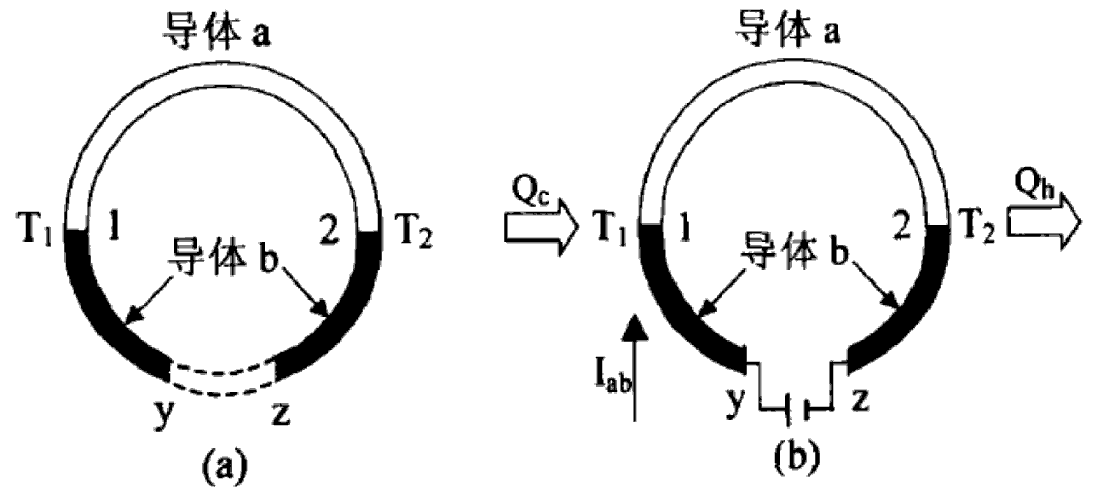
图1.1 Seebeck效应和Peltier效应示意图

1.2.2 Peltier效应

1834年，法国科学家C.A.Pletier发现，将电流通入两个不同的导体构成的闭合回路时在两个不同导体的接触处会有吸热和放热的现象出现，即Seebeck效应的逆效应，称为Peltier效应^{[10, 11]}。同时，吸热和放热的多少取决于这两种不同导体的性质和接触处的温度。如图1.1所示，在a、b两种不同的导体构成的一个回路中，若在y，z的两端施加一个稳定的电压，在两个导体的接触处1和接触处2的位置将会出现一处吸热，另一处放热的现象，若改变电压的正负极方向，即改变回路中电流的方向，则吸热和放热现象也将随之改变，施加的电能即可转变为热能，转变后的热量就被称为Peltier热量。实验表明，吸收或放出的热量，只由材料本身的性质和接触处的温度决定，并且其速度与电流I成正比，即：

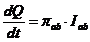(1.3)

式中_ab为比例常数，被定义为Peltier系数，单位一般为W·A^-1。当 dQ gt; 0，则_ab为正，反之为负。_ab的大小与接触处的温度有关，是关于温度的函数。帕尔帖效应的物理本质是由于载流子在组成闭合回路的不同导体中存在势能高低的差别，当载流子穿过不同导体的接触面时，为得到一个新的平衡状态，在接触处周围将会与晶格产生能量交换，于是就表现出吸热或放热现象^[12]。

1.2.3 Thomson效应

Thomson效应在1854年被Thomson发现，即当电流通入一个单独的导体且此导体中有温度梯度的存在，该导体就会与环境之间发生热交换的现象，如图1.2所示^[11]。Thomson系数可表示为：

(1.4)

其中， dQ/dt为单位时间内吸收或放出的热量， dT/dx为温度梯度，I为通过的电流。即Thomson系数与吸收或放出的热量成正比，且与通入的电流方向和温度梯度的方向有关。

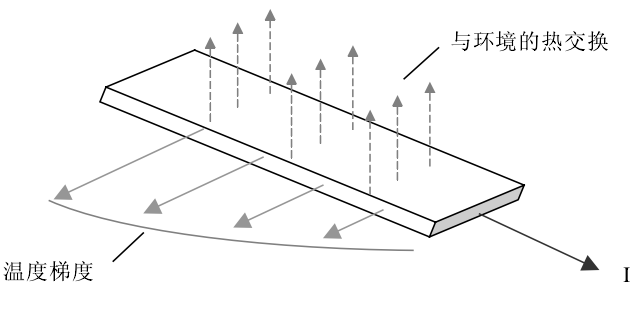
图1.2 Thomson效应示意图

Peltier效应和Thomson效应存在相似之处，都可用于热电制冷或制热。若导体中通入的电流方向与温度梯度方向相同，导体就会向外界放出热量，Thomson系数都为正，反之导体就会吸收外界的热量，Thomson系数为负。在产生机理方面，Pettier效应是由于不同导体中的载流子势能存在差异引起的，而Thomson效应则是由均匀单一导体中的温度梯度引起的。

1.2.4 Kelvin关系

上文中介绍的三种热电效应均为可逆的，同时Seebeck系数、Peltier系数和Thomson系数之间使相互联系的，而并非互相独立。可用Kelvin关系式表示^[13]：

(1.5)

(1.6)

其中为两种不同材料的Seebeck系数的差值。通过测量Seebeck系数和绝对温度根据式1.5与式1.6即可计算出Peltier系数和Thomson系数。

1.3 热电材料性能参数

热电器件的热电转换效率是研究者们最关心的参数，它可以决定一种热电材料是否能够得到大规模的应用。通常在不考虑热电器件之间的能量交换损失的情况下，热电转换效率可以表示为:

(1.7)

其中为高温端温度，为低温端温度，ZT值代表材料的热电性能指数(见下文)。由式1.7可知，提高材料的ZT值和增大高、低温两端的温度差都可以提高其转换效率。

二十世纪初，德国科学家阿特克希(Altenkirch)提出了比较完善的热电模型理论：材料的热电性能高低与材料的Seebeck系数，电导率σ和热导率κ有关，可以用无量纲热电优值ZT来表征材料的综合热电性能^[14]，具体表示为：

(1.8)

从式1.8可以看出，若只考虑某一个参数的变化，热电材料在一定的温度下，增大Seebeck系数α，提高电导率σ以及降低热导率κ，都会使热电优值ZT变大，得到较高的热电性能。这三个参数对热电优值ZT的影响如图所示，同时这三个参数还与材料中的载流子和晶格声子有关^[15]。

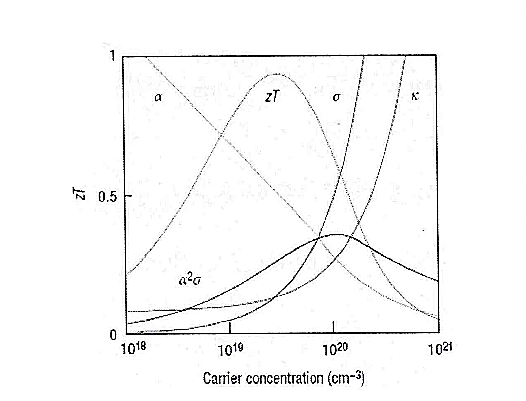
图1.3 热电优值及各参数与载流子浓度的关系示意图

1.3.1 Seebeck系数

热电材料的Seebeck系数α是指由于Seebeck效应而产生的温差电动势与温差之间的比值^[16]。它反映了材料中载流子之间的相互作用的强弱和载流子运输速率的高低，与载流子浓度和散射有关。。

采用弛豫时间近似，假设载流子服从经典统计理论，利用抛物线型能带模型，Seebeck系数可以表示为^[17]：

(1.9)

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：