摘 要

随着非贵金属化合物析氢材料的研究不断推进，包括过渡金属磷化物被证实具有高储量、优异性能等优点，其中磷化镍更是被发掘出优异的催化活性。通过对于一系列磷化镍的研究得知，Ni₃P这一最富镍的磷化镍，作为氢催化反应的阴极材料的前景巨大。材料改性方面，阴离子空穴调制为常用手段，但阳离子空穴调制机制方面的研究鲜有报道。本课题拟利用材料计算与模拟技术，研究不同浓度和位置的镍空位，通过多种描述符比较引入镍空位前后Ni₃P析氢催化能力的变化，来探究镍空穴对于Ni₃P催化产氢性能的影响。所得结果对于非贵金属催化材料缺陷改性以及阳离子空穴调制机制有一定的研究意义。

结果表明，通过对Ni₃P（110）面上不同活性位点的研究，镍空穴的引入对于Ni₃P的催化析氢能力有一定的提升，提升幅度与空穴浓度以及位置相关。并据此对于镍空穴调制机制提出了自己的猜想。

关键词：Ni₃P，空穴调制，电催化产氢，第一性原理，密度泛函

Abstract

With the development of non-precious metal compounds for hydrogen evolution, transition metal phosphides have been proved to have many advantages like high reserves and excellent properties et al. Among them, nickel phosphide has been found to have excellent catalytic activity. Through the study of a series of nickel phosphide, Ni₃P, the most Ni-rich nickel phosphide, has great prospects as cathode material for hydrogen catalytic reaction. In the aspect of material modification, anion hole modulation is a common method, but there are few reports on the mechanism of cation hole modulation.In the study, in order to investigate the effect of nickel vacancies on the catalytic performance of Ni₃P for hydrogen production, the material calculation and simulation techniques were used to study the nickel vacancies at different concentrations and locations. Various descriptors were used to compare the catalytic capacity of Ni₃P for hydrogen evolution before and after the introduction of nickel vacancies. The results have certain significance for the defect modification of non-noble metal catalytic materials and the mechanism of cationic hole modulation. The results show that the introduction of nickel holes improves the catalytic hydrogen evolution ability of Ni3P by studying the different active sites on the surface of Ni3P (110), and the increase range is related to the concentration and location of the holes. Based on this, the mechanism of nickel hole modulation is proposed.

Key words: Ni₃P, vacancy modulation, HER, first principles, DFT

目 录

第1章 绪论1

1.1研究背景1

1.2国内外研究现状1

1.3研究内容及意义3

第2章 实验计算的基本原理3

2.1第一性原理3

2.2密度泛函理论4

2.3电催化析氢反应介绍5

第3章 实验计算过程5

3.1 实验参数设置5

3.2 计算过程6

3.3 氢催化能力表征8

第4章 实验结果与分析9

4.1几何结构变化9

4.2电子结构变化10

4.2.1电荷密度分析10

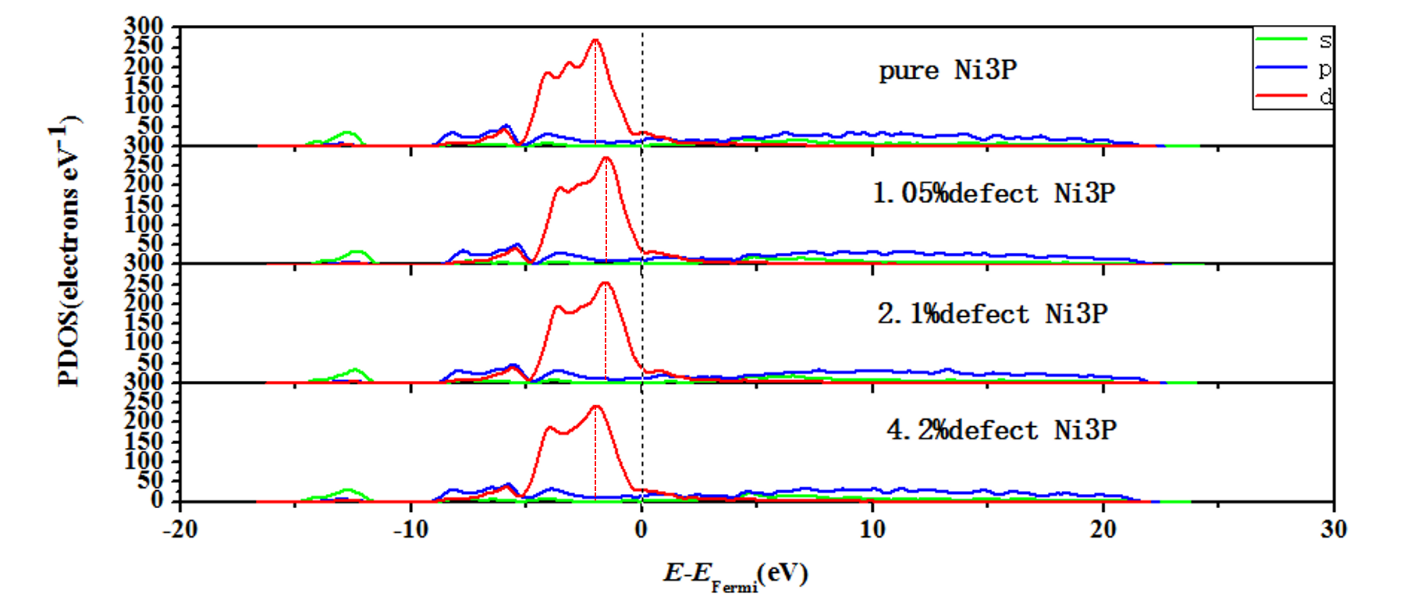
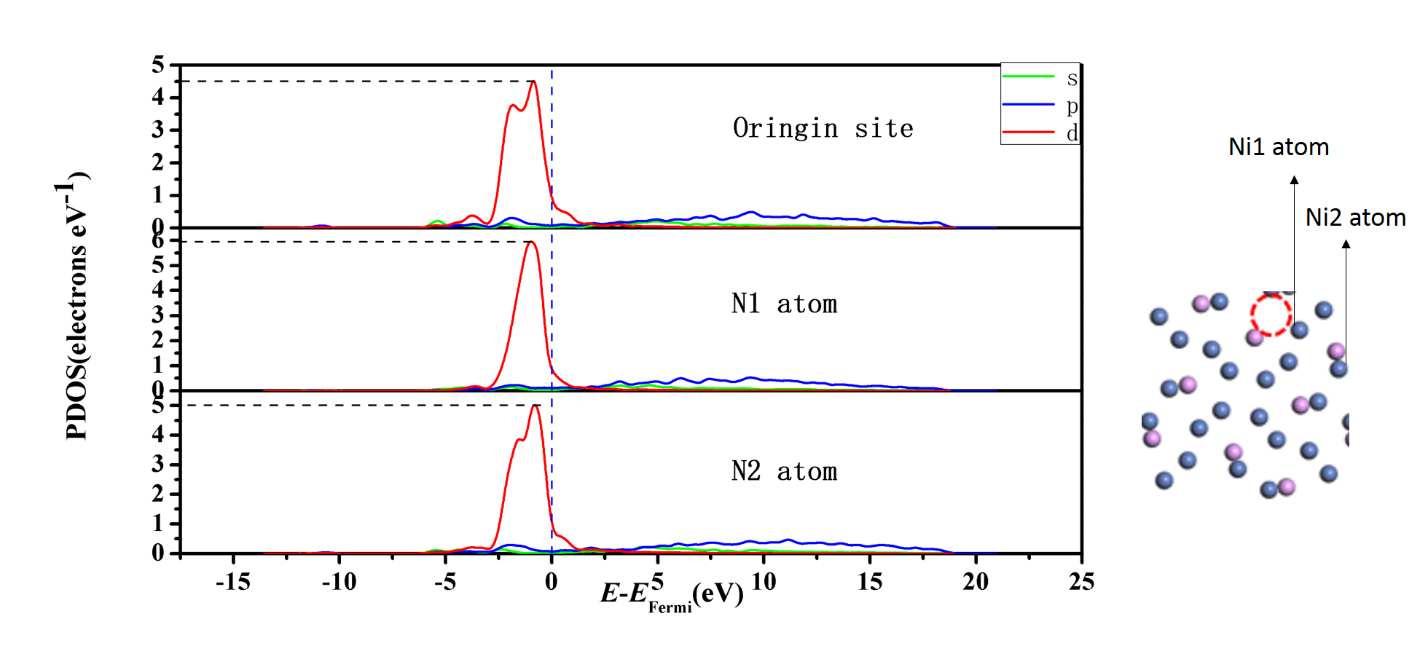
4.2.2态密度图分析11

4.3氢吸附自由能变化13

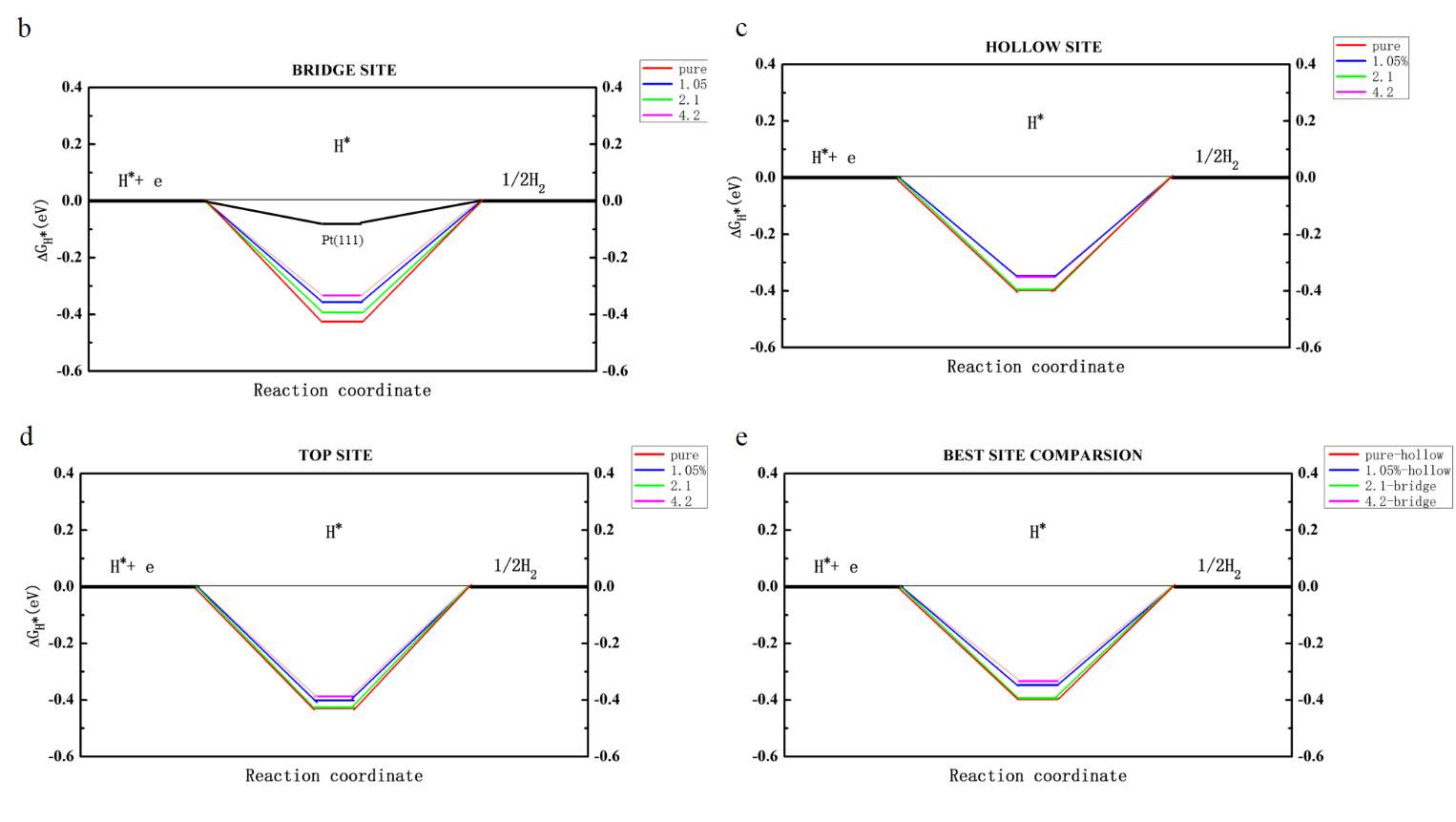
4.3.1不同缺陷浓度下的比较13

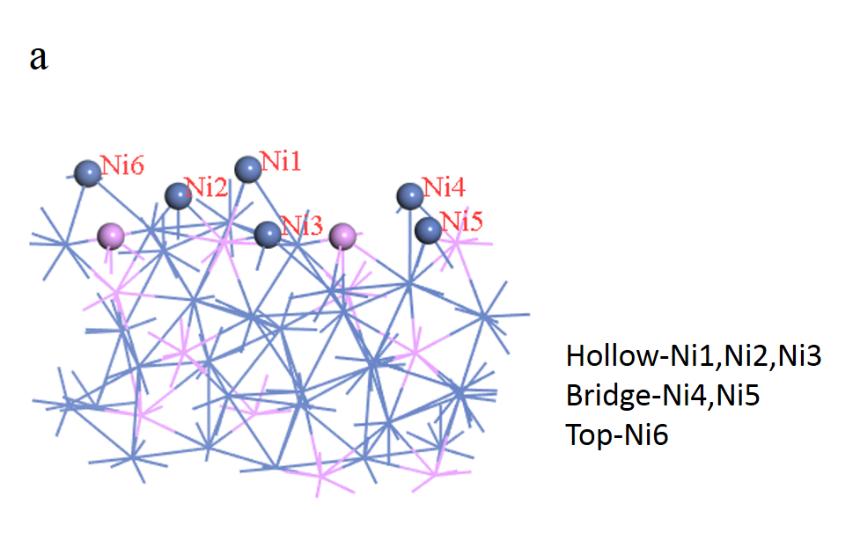
4.3.2不同缺陷位置下的比较15

4.4空穴调制机制的分析17

结论与展望20

参考文献21

致谢22

第1章 绪论

1.1 研究背景

能源短缺是21世纪以来人类社会发展所面临的一大难题。氢能源作为一种储量丰富、性能优越、用途广泛的新型能源，其发展得到了各国的高度重视。全世界来看，部分发达国家，如日本、德国等，已实现部分领域的氢能源商业化应用，特别是在交通领域。截至2017年12月，全球燃料电池乘用车销售累计接近6000辆。丰田Mirai共计销售5300辆，其中美国2900辆，日本2100辆，欧洲200辆，占全球燃料电池乘用车总销量的九成以上。在我国，各地近年来也在积极发展氢能源技术与配套工业设施，响应国家号召，努力实现氢能源产业可持续发展。据最新的由中国氢能联盟发布的《中国氢能源及燃料电池产业发展研究报告》显示^[1]，到2050年，氢在我国终端能源体系占比至少要达到10%，成为我国能源战略的重要组成部分。

在这种前提下，氢气的制备无疑是制约整个氢气能源发展的重要环节。氢气可通过多种途径制备，目前工业上用以制备氢气的方法包括水煤气法制氢法、电解水制氢法、火油热裂合成气法等。由于未来着重建设环保型社会，而利用电解水的析氢反应（HER），长期以来被广泛看作一种环境友好的技术路线，因此成为当前氢气生产工业中，研究热点较高的一种制氢路线。但这种路线也存在着不足，在电解水制氢过程中，当电极的析氢过电位偏高时，会导致总工业耗能较大，不利于工业化生产。因此研究拥有较低析氢过电位的电极材料是整个电解水制氢产业的关键所在。大量研究表明贵金属材料Pt拥有优异的性能，然而其高昂的成本制约了在工业上的应用。与之相比，过渡金属化合物在氢催化性能上可通过掺杂等材料改性手段来获得提高，同时在成本上有着无可比拟的优势，因此得到各研究机构广泛重视。

而随着计算机技术的飞速发展，其与其他科学技术的交叉应用已成为当下进行科学探索的主要手段之一。在材料学方面，当我们考虑到对现有材料的理论改性，或是基于过往经验来预测新材料的发展时，计算机更是优秀的辅助工具。基于上述背景，本课题旨在利用计算模拟探究空穴调制对于Ni₃P这一非贵金属化合物产氢性能的影响。

1.2 国内外研究现状

基于前文所提到的电解水制氢的关键所在，大量研究目标为寻找拥有较低的氢超电势，同时催化活性高的金属或合金。从能量角度来考量，当在平衡电极电势附近时，通常吸附氢能力较弱的金属或合金，会表现出较高的催化活性。一般认为，吸附金属d成分越高，而不成对的d电子就较少，其与氢吸附键也较弱。而在过渡金属原子中，由于存在可形成化学吸附的空d电子轨道，这与有氢原子吸附过程的析氢电极反应对电极的要求相吻合^[2]。基于此种原因，大量析氢反应的催化电极选择对象主要集中在过渡金属及其化合物上。设计电化学催化电极的主要任务可以概括为：选择合适的过渡金属原子，以及构筑合适的反应环境，兼顾催化电极的导电性、电化学稳定性和催化活性。

研究表明，贵金属Pt及其合金具有优异的电催化析氢活性^[3],[4]，其氢超电势低，但由于贵金属Pt在大自然中储量较少，导致在工业生产中使用成本无法控制，不适宜大量氢气的生产。因此对于成本较低的非贵金属催化剂的研究就显得十分重要。在用于电解水的阴极材料中，包括过渡金属及其碳化物，硼化物、氮化物、二硫化物，和磷化物等在内的一系列材料，由于具有自然储量丰富，催化活性高，稳定性好等诸多优点而在电化学催化剂领域引起了广泛关注。JinJia等人^[5]研制出分级结构石墨烯多孔微米棒负载Mo2C用作高效析氢电催化剂，该Mo2C/ CLCN催化剂的电催化析氢活性及稳定性远高于同等条件下不含非金属掺杂元素时的纯相Mo2C催化剂。在0.5 M H2SO4中，Mo2C/ CLCN具有低的起始电位（-85 mV）和塔菲尔斜率（48.2 mV/dec），达到10 mA/cm2的电流密度仅需要145 mV的过电位，并能在高达50 mA/cm2的电流密度下保持12小时而不发生显著的电流密度衰减。Qiuyu Ma、Chengyi Hu等人^[6]将泡沫镍基底上的Ni(OH)₂纳米片进行高温硫化处理，得到了生长在泡沫镍上的NiS₂纳米片（NF-NiS₂），并在此基础上设计出性能优异的电催化剂应用于搭建全电解水装置，测试其电解水产氢性能，在1M KOH溶液中达到10 mA cm^-2的电流密度低至67 mV，塔菲尔斜率为72 mV/dec。近期Jinsong Wang、Jia Liu等人^[7]采用简单的电化学沉积和固相磷化两步反应，设计并成功制备了镍掺杂的磷化钴（Ni0.1Co0.9P）三元纳米片电催化剂。相比于纯的Ni2P和CoP，掺杂后的材料在中性条件下同时展现出优异的水还原和氧化电催化活性和稳定性。在中性电解液中，其水还原电流密度达到10 mA/cm2时所需电势为125 mV，而其水氧化反应在电流密度达到10 mA/cm2时所需电势为1.79 V，展现出与商业Pt/C和Ir/C电催化相媲美的催化性能。

过渡金属磷化物作为非贵金属催化剂的一种，具有发掘优异的催化活性的前景。磷化镍（NixPy）是过渡金属磷化物中最有希望的候选物之一，其结构多样，且在酸性溶液中拥有高度耐腐蚀性。Ni₃P作为最富Ni的磷化镍，近期被研究出可作为氢催化反应的阴极材料^[8]。Jin等人报道了Ni₃P多孔空心纳米球的HER性能，表明其具有良好的催化性能。在酸性溶液中，达到20mA cm-2的电流密度所需的过电位仅为99mV^[9]。在过往的研究中，有研究人员探究了不同类型的磷化镍(Ni12P5、Ni2P和Ni5P4)的HER的电催化性能，发现其催化性能顺序为Ni5P4gt;Ni2Pgt;Ni12P5，在10mA cm-2的电流密度下，其电势分别为118、137和208mV^[10]。由此有人认为富镍磷化物具有较差的HER活性。然而，Ni₃P作为最富Ni的磷化物在实验中表现得更为活跃。由此，Jun Hu等人对于Ni₃P的不同平面，尤其是非化学计量平面在氢催化反应中的表现，利用第一性原理进行了计算，进行了较为全面的理论研究。研究表明，Ni₃P的部分非化学计量比表面，如（110）B与（111）A，拥有良好的电催化活性、合适的电位和高的稳定性，但其表面活性位点较少^[11]。

在对于材料改性的多数研究中，常通过增加阴离子空位来增加活性位点。如对过渡金属氧化物进行氧空位调制来获得更好的电催化制氧性能^{[12], [13]}，或是通过增加多层硫化物中的硫空位来增进其HER性能^[14]。但由于金属空位形成能高，对于金属阳离子空穴调制的研究较少，对于其如何影响HER性能也不清楚^[15]。

1.3 研究内容及意义

由于关于金属阳离子空位对材料的电催化析氢影响的研究不多，对于其机制也不明了。传统的实验手段可能会面临制备周期长，测试周期长等问题，不适宜作为此次的毕业设计的研究手段。而随着现代物理、数学等基础理论科学不断发展完善以及计算机运算能力的大幅提高，计算机模拟材料设计在材料学研究中扮演了越来越重要的角色。传统的技术手段受到多种因素制约，对于原子级系统中的相关物理特性也难以把握其变化。而通过第一性原理以及密度泛函理论近似来进行模拟计算，复杂的多粒子体系的电子结构与物理性质也得以呈现。

基于此，本课题通过模拟计算设计具有一定空穴浓度的Ni₃P晶体，利用第一性原理计算表征增加空穴前后晶体的HER催化性能，进行分析比较，来探究空穴调制对Ni₃P催化产氢性能影响。研究主要分为三个部分：（1）通过实验参数设置测试，来完成对于不同镍空穴浓度以及不同镍空穴位置的Ni₃P模型的构筑与优化；（2）从几何结构、电子结构以及其他氢催化性能描述符等多个方面比较空位调制的作用；（3）通过分析空位调制前后的催化性能差异，来探究空穴调制对于Ni₃P催化产氢性能的影响机制。

第2章 实验计算的基本原理

2.1 第一性原理

凝聚态物质，即物质能量足够低以至于凝聚成稳定的原子核分子体系，是组成我们这个世界的基础。传统的材料研究方法，往往是通过实验观测，来综合分析宏观现象，并提炼出经验模型或是半经验模型去归纳总结。这种方法易于理解物理系统的规律，以及可以通过合理推理去预测系统的行为，但由于缺乏对本质的认识，难以建立准确的模型。而第一性原理计算(First Principles Calculation)更注重本质，这种方法从构成物质的基本粒子入手——即原子核以及电子。认为原子核与核外电子之间的相互作用，决定了原子之间相互作用，即各类化学键。宏观物质的物理性质都取决于这些基本相互作用。第一性原理计算的手段是求解薛定谔波动方程（Schrouml;dinger equation） ^[16]。其核心在于根据实际需求选用合适的近似方法。上世纪二十年代，物理学家薛定谔提出薛定谔波动方程，这一二阶偏微分方程将物质波的概念和波动方程进行综合考量并结合描述，用来解释微观粒子的运动，使得每一个微观多粒子系统都能与特定的薛定谔波动方程对应。从而通过求方程定解，获得微观系统的性质。薛定谔波动方程具体定义如下：

（2.1）

式中，ħ是约化普朗克常量，mu;表示粒子质量，V(r)表示粒子势场，Psi;(r,t)为系统波动函数，r和t分别为体系中电子和原子核的坐标位置。在实际应用时由于薛定谔方程在求解复杂的体系时过于困难，研究人员因此提出不同的近似方法，如波恩-奥本海默绝热近似 ^[17]、Hartree-Fock近似 ^[18]、密度泛函理论（DFT）等等。其中密度泛函理论将多电子问题简化为单电子进行处理，通过基态电子态密度描述体系的物理性质。由于这一理论发展成熟，化繁为简，在多个领域得到了广泛应用^[19]。

2.2 密度泛函理论

在物理、化学和材料科学中，当研究对象为研究多体系统时，密度泛函理论由于化繁为简的特性，成为了最常用的建模方法。求解多电子系统的性质可以通过使用泛函，即另一个函数的函数来确定，在密度泛函理论中，该对象函数是空间相关的电子密度，而非一般薛定谔方程中所用到的多电子波函数。这种处理正是这一理论的核心所在，大大简化了计算过程。从计算量上来看，由于每个电子的空间变量数为3，因此对于电子数为N的系统，其多电子波函数共有3N个变量，这无疑非常难以求解。而电子密度这一函数只拥有三个变量，因此在计算时更方便处理^[20]。自二十世纪七十年代以来，密度泛函理论在固体物理计算中已经非常流行。密度泛函理论起源于Thomas-Fermi模型，但由于其忽略了电子相关能，在进行动能和电子交换能的计算时往往导致了较大误差。密度泛函理论在Hohenberg-Kohn定理^[21]提出之后有了严谨的理论解释，也为更多人所接受并应用在研究中。

Hohenberg-Kohn定理对一切在外部势下运动的电子系统适用，其第一定理指出体系的基态能量是电子密度的唯一泛函，由此可推断基态密度唯一地决定了系统的势能，从而决定了系统的所有性质，包括多体波函数^[21]。Hohenberg-Kohn第二定理通过最小化体系能量来求得基态能量，是关于基态密度的泛函，。H–K定理由Walter Kohn和沈吕九进一步发展以产生Kohn–Sham DFT方程（KS-DFT）。在这个方程里，将静态外电势中电子相互作用的这一难以求解的多体问题，转换为在有效势中运动的非相互作用电子的可处理的问题。有效势包括外部势、以及电子间的交换作用和相互作用。KS-DFT中的难点在于对于交换作用和相关作用的建模。为了解决这个问题，研究中比较常用的，也是较为简便的方法之一为局域密度(LDA)近似。

LDA近似是密度泛函理论中用以求解交换-相关（XC）能量泛函的一类近似，与其他近似相比，这一理论的变量为空间中每个点的电子密度值，而非密度的导数或Kohn-Sham轨道。有多种方法可以得到相关能和交换能的局部近似值。然而，绝大多数成功的应用证实，均匀电子气体（HEG）模型是非常行之有效的。在LDA近似下，体系的交换能部分可通过均匀电子气模型来计算，而相关能部分则采用对自由电子气模型进行分析求得。到目前为止，尽管密度泛函理论仍然在不断改进，但是在计算半导体的能带宽度^[22]，或是描述分子间作用力，特别是研究某些强关联系统时，还存在一定的误差，因此在未来这一理论还需要通过改变泛函等手段来进一步完善。

2.3电催化析氢反应介绍

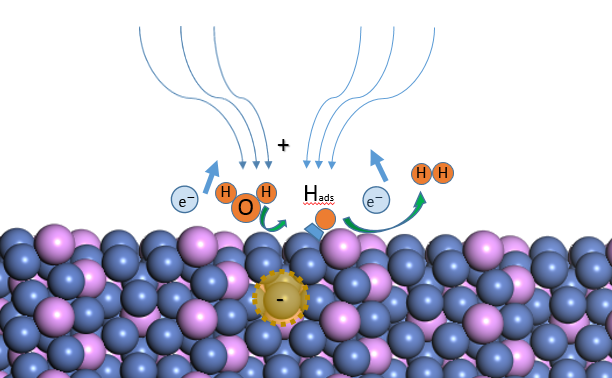
电催化析氢反应指通过电化学的方法使用催化剂产生氢气，在电解水反应中发生在阴极。由多步基元反应组成, 酸碱环境中反应机制基本相同,不同之处在于酸性电解液中质子来自H₃O , 碱性电解液环境里则是由H₂O提供。以酸性电解液环境中电催化析氢反应为例, 反应通常分为两步，第一步为Volmer反应，第二步为Heyrovsky反应，或是Tafel反应，二者关系为平行，表示吸附态氢原子以两种可能的方式从电极表面脱附。具体方程如下

Volmer 反应：

(2.2)

Heyrovsky反应（电化学脱附）:

(2.3)

Tafel反应（复合脱附）：

(2.4)

第一步Volmer反应中发生电子的转移, 质子（）从电解质溶液中得到电子，在电极表面形成吸附态氢原子()。之后将会进行第二步反应，Heyrovsky反应表示电化学脱附，即吸附态氢原子与电解质中的质子结合产生氢气。与之平行的Tafel反应则是复合脱附反应,电极上吸附态氢原子相互结合生成氢气。从动力学方面对电催化析氢反应进行分析，见式（2.4），为Tafel公式，已知氢超电势和电流密度之间在一定范围内存在定量关系：

(2.4)

式中为总氢超电势，j为电流密度，a表示单位电流密度下的氢超电势值，其影响因素为电极材料种类、电极表面状态、溶液温度等，b为Tafel斜率，对大多数金属来说是一通用常数。当阴极材料为氢超电势大的金属时，电子转移速率较慢，此时电子转移步骤成为影响整个反应速率的关键,反应机理为迟缓放电机理。而 如果电化学脱附是反应中的慢速步, 则被称为电化学脱附机理。与之相应，如果复合脱附是反应中的慢速步, 则被称为迟缓复合机理。不同的机理下可画出的Tafel公式曲线不同，对应的Tafel斜率的范围也不同，因此, 实际情况中可以根据Tafel斜率的大小来推测电化学反应动力学过程机理^[23]。

第3章 实验计算过程

3.1 实验参数设置

计算模拟方面用到的是Materials Studio (Accelrys Inc.)的Castep模块。参考Jun Hu等人的研究^[11]，以及自己的尝试，最终确定本次研究所需要的具体参数。本次计算基于自恰周期性DFT计算了对象的电子结构以及不同平面的催化活性。计算交换相关能方面选择Perdew-Burke-Ernzerhof（PBE）近似作为广义梯度近似（GGA）方法。进行吸附的表面来自于完成优化的不同缺陷浓度的Ni₃P模型，设置真空层厚度为15Aring;.。几何优化时截断能为380.0eV，SCF收敛值设为1.0*10-6 eV，当energy, maximum force, maximum stress以及 maximum displacement 四个精度参数分别小于5.0*10-6 eV, 0.01 eV Aring;^-1, 0.02 GPa 以及5.0*10 -4Aring;时视为优化完成。对于体对象的k点设置为2*2*3,以平面对象计算时则是2*2*1。

3.2 计算过程

初始Ni₃P模型取自Material Project（www.material project.org），进行几何优化后得到本征Ni₃P模型，蓝色球为镍原子，紫色球为磷原子，见图3.1，右侧为Ni₃P结构示意图。

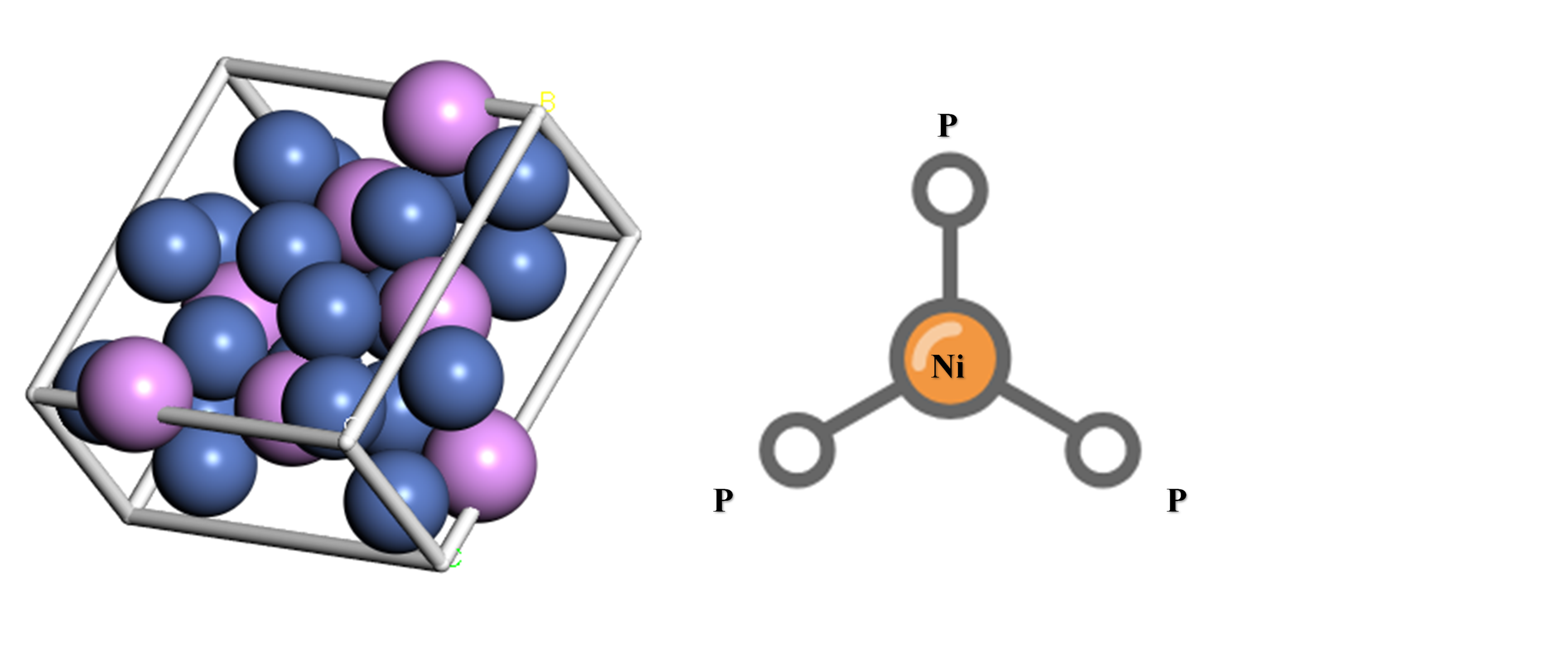
图3.1 本征Ni₃P模型及结构示意图

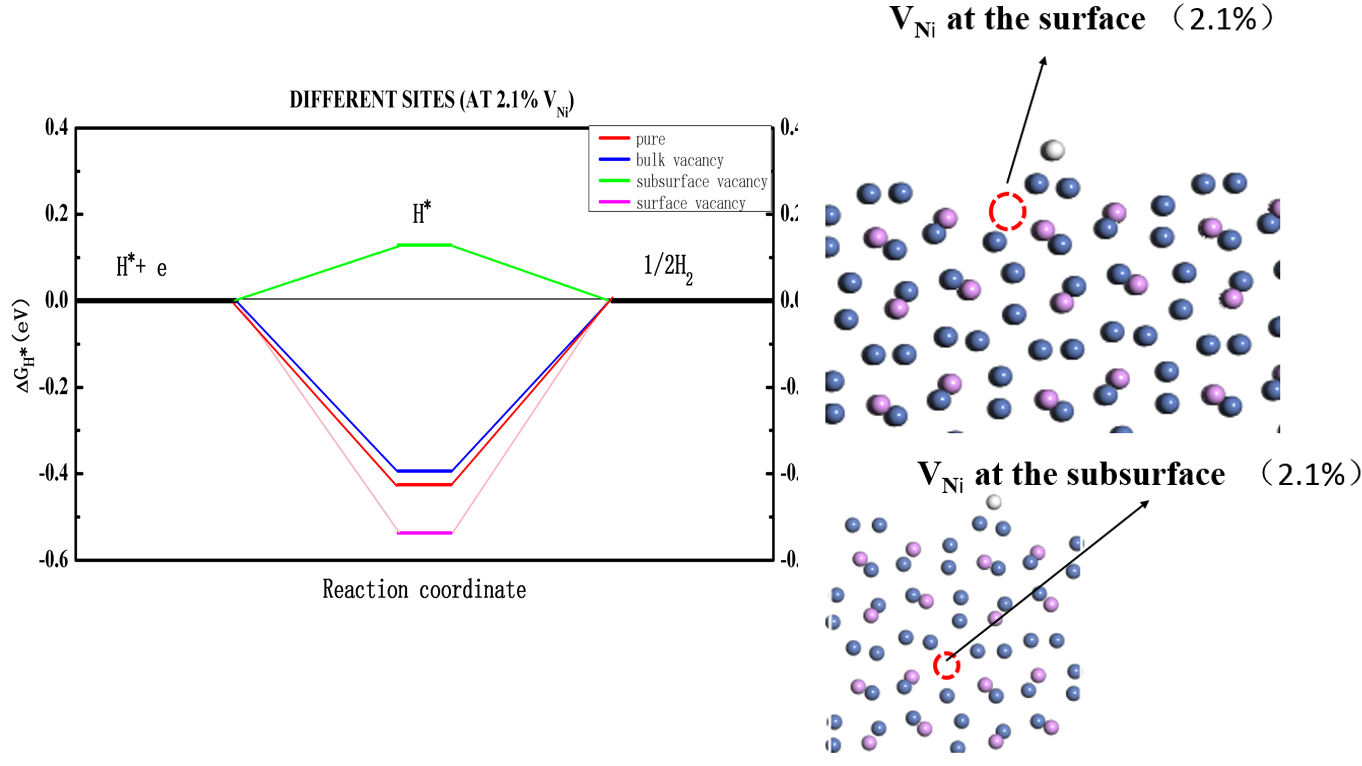
图3.2为不同镍空穴浓度的Ni₃P模型。依照各模型原子数，按照0%、1.05%、2.1%、4.2%来设置不同浓度的镍空穴按照镍空穴所处位置的不同，可分为表面镍空穴和体相镍空穴，表面镍空穴按照与表面的距离，还可分为表面镍空穴和次表面镍空穴。本次研究中，在分析几何结构与电子结构时，所引入的皆为体相镍空穴，并建立大体积超胞（2*2*2 supercell，192原子），以减少由于空位在特定位点带来的影响。

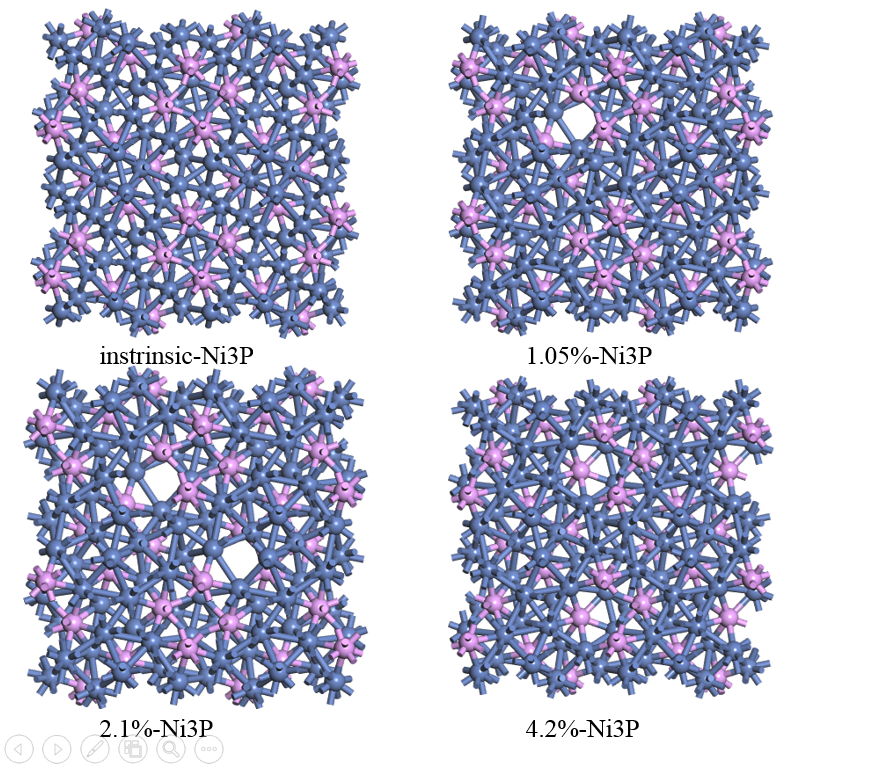
图3.2 不同镍空穴浓度的Ni₃P模型

图3.3为截取的部分模型的能量平衡曲线图。根据castep的软件说明，当max force, max displacement, energy change, max stress四个参数都收敛于自设的标准时，即视为优化完成，此时读取castep文件里体系的能量等数据可进行数据处理与分析。

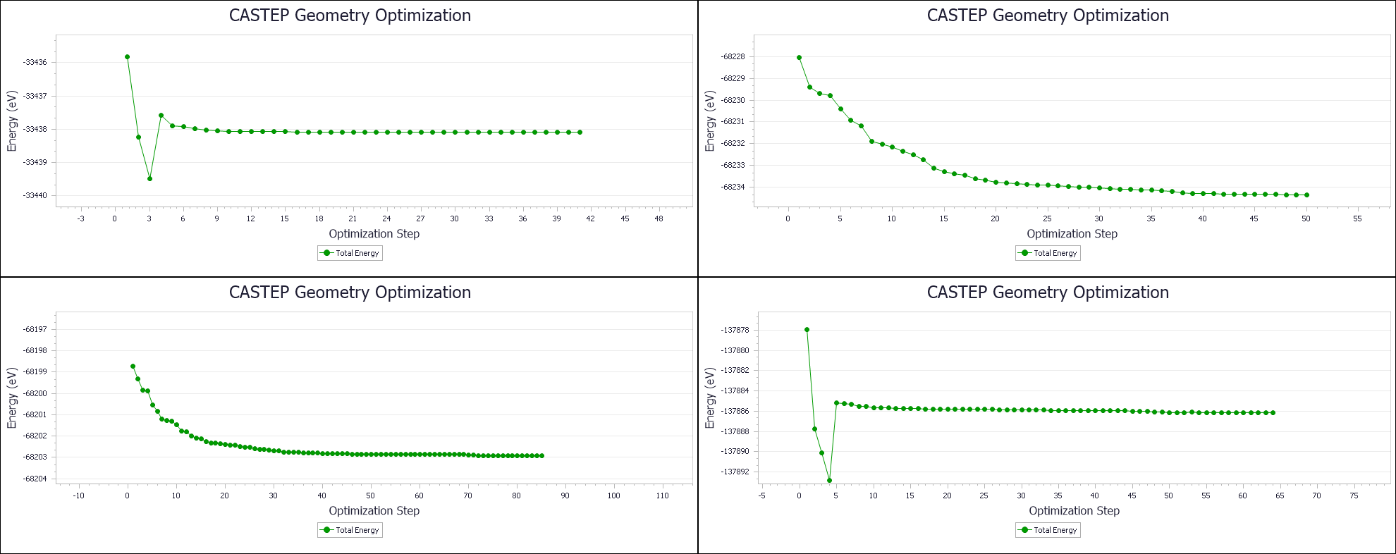
图3.3 部分模型的能量平衡曲线

3.3 氢催化能力表征

为了描述催化反应的程度，以及比较催化剂的作用，从事理论催化的科学家们在长期的研究过程中提出了各种各样的描述符，包括原子序数、最外层电子束、d轨道占据数、功函数、吸附能等等。在此为了具体体现空位的引入对材料催化能力的影响，我选择了两种较为常用的描述符来进行表征。首先是“d能带中心值（d-band center）”这一描述符。大量的研究表明，过渡金属及其化合物催化剂的催化能力强弱与其d能带中心电子有密不可分的关系^[24]，在经过长期的发展之后，d能带中心值的概念由Norskov提出^[25]。d能带中心值可以理解为d电子的平均能量，在解释过渡金属催化剂的活性方面有很强的指导意义。其计算公式为：

_d (3.1)

值越正，可认为具有越强的催化能力。

第二个描述符为“氢吸附自由能（△G）”。在析氢反应过程中, 氢原子在催化剂表面的吸附和脱附是一对竞争反应。若吸附太强, 易于形成氢气，但不利于氢气的排出，若吸附太弱, 不利于形成氢气。只有在吸附和脱附之间达到良好的平衡, 才能表现出较好的析氢活性^[23]。氢吸附自由能作为Volmer–Tafel析氢反应动力学机理下一个成功的描述符^[26]，其公式为：

(3.2)

(3.3)

式（3.2）中表示系统的零点能，表示温度T与该温度下的熵变的乘积，二者均可在castep中计算得到。代表体系吸附一个氢原子时所需增加的能量，由式（3.3）计算得到，表示Ni₃P平面与吸附原子的总能量，表示Ni₃P平面的能量，表示氢气分子的能量。通常来说，绝对值越小的△G_H代表着越好的氢催化能力。在本次试验中，根据计算完毕的castep文件，项计算值为0.392eV。在之后的计算中作为常数项处理。

第4章 实验结果与分析

4.1 几何结构变化

表4.1为不同缺陷浓度的模型在几何优化前后的结构参数变化，其中native-Ni₃P表示用于计算的未优化的初始Ni₃P模型，intrinsic-Ni₃P为无缺陷的Ni₃P模型，其他不同缺陷浓度的模型都是在instrinsic-Ni₃P的基础上进行镍空穴的引入后，再用相同的参数进行几何优化得到。表4.2为不同缺陷浓度的模型优化后空穴周围的键长变化。

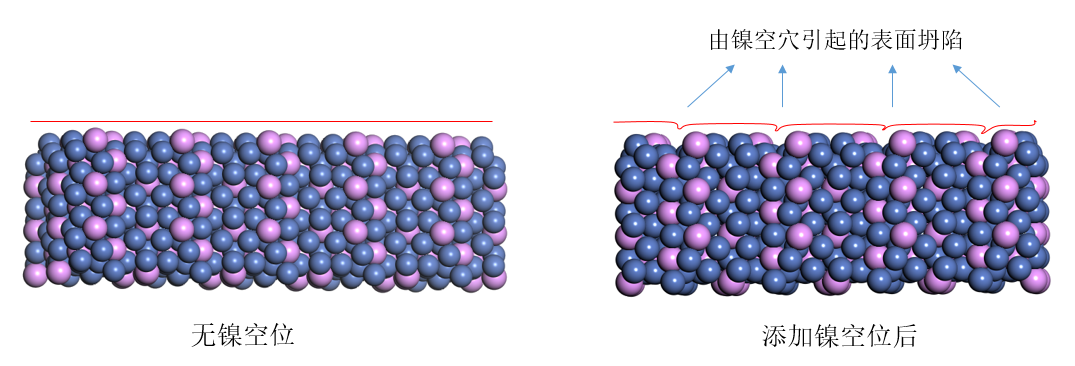
由表4.1可以看到，经过优化后的intrinsic-Ni₃P模型，与未优化的初始模型相比，尺寸变化率在5%以内，说明优化参数合适。随着缺陷浓度的增大，晶胞边长参数发生了变化，模型体积在逐渐变小。由表4.2可以看到，在引入缺陷后，镍空穴周边P原子与周边Ni原子形成的Ni-P键键长变短，周边Ni原子与周边Ni原子形成的Ni-Ni键键长也变短，表明P原子倾向于远离这个空位，并通过与其他原子形成更强的键来维持结构的稳定。参考其他对于缺陷模型的结构的研究^[27],[28]，同时结合对于Ni₃P结构的分析，可以推断当镍空穴被引入时，会在空穴周边产生局域化的结构畸变，以达到结构稳定。当内部镍空穴缺陷增多时，会导致模型进一步坍缩以达到能量最小状态。

表4.1 不同缺陷模型几何参数变化

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：