英语原文共 8 页，剩余内容已隐藏，支付完成后下载完整资料

具有大忆阻器交叉开关的模拟信号和图像处理

Can Li ¹，Miao Hu^2,5，Yunning Li¹，Hao Jiang¹，Ning Ge³，Eric Montgomery²，Jiaming Zhang²，Wenhao Song¹， NoraicaDaacute;vila² ，Catherine E. Graves²，Zhiyong Li²，John Paul Strachan²*，Peng Lin¹，Zhongrui Wang¹，Mark Barnell⁴，Qing Wu⁴，R.Stanley Williams ²，J.Joshua Yang ¹*和Qiangfei Xia¹*

忆阻器交叉开关提供可重新配置的非易失性电阻状态，可以消除矢量矩阵乘法中的速度和能量效率瓶颈，这是信号 和图像处理中的核心计算任务。然而，由于设备工程和阵列集成的困难，使用这样的系统将模拟 - 电压 - 幅度 -矢量乘以模拟电导矩阵以相当大的规模已经证明是具有挑战性的。在这里，我们展示了由金属氧化物半导体晶体管 顶部的氧化铪忆阻器组成的可重构忆阻器交叉开关，能够进行模拟矢量矩阵乘法，阵列尺寸高达128times;64单元。我们 的输出精度（5-8位，取决于阵列大小）是高器件良率（99.8％）和忆阻器的多级稳定状态的结果，而线性器件电流 - 电压特性和单元之间的低线电阻导致高精度。利用大型忆阻器交叉开关，我们展示了信号处理，图像压缩和卷积滤波，这些都是物联网（IoT）和边缘计算发展的重要应用。

随着互补金属氧化物半导体晶体管（CMOS）技术接近工艺规模的终点，数字处理器的能耗和吞吐量的提升正在达到稳定水平^1,2.此问题会影响大型数据中心或云的电源要求，还会限制物联网（IoT）传感器和执行器的有效部署^1,3 由于通信带宽有限和数据传输成本高，没有办法传输和存储现在收集的所有数据用于集中分析，并且随着物联网的发展，预计这一挑战将随着设备数量级的增加而增长。结果是网络边缘需要足够的智能⁴ 预处理数据并仅将最重要的信息传输到云。这种边缘计算必须非常节能，因为它可能仅取决于它可以从其环境中清除的能量。因此，新的计算设备和方法至关重要，特别是那些可以直接与嵌入式传感器的模拟输出接口进行过滤，分析，在传输之前压缩，编码并可能加密数据。

其中许多操作可以表示为矢量矩阵乘法（VMM），期原则上可以通过忆阻器交叉开关阵列在模拟域中执行^5–10 使用欧姆定律进行乘法运算和基尔霍夫现行定律的总结11^11–30 （图.1a）。正在开发这种VMM作为用于推断深度神经网的加速器^31-35，但也可以用作边缘计算的可重构造模拟处理器。来自传感器的电压矢量可以直接应用于可以直接应用于忆阻器开关的行上。其中适当的矩阵元素的值已被存储为单元的电导。如果互连线的串联电阻与忆阻器电阻相比可忽略不计，则实时出现在阵列列上的电流表示乘法的输出矢量。要并行读出结果，当前信号来自每列的信号通过跨阻放大器（TIA）转换为电压信号，该放大器也用作虚拟接地。

到目前为止，这个概念的演示仅限于二进制信号输入和/或二进制矩阵权重^14–16.最近，脉冲宽度代替振幅用于表示模拟输入信号^27–30但是这种方案需要更多的读出时间和更复杂的集成电路。据我们所知，模拟 - 电导 - 矩阵乘积的模拟 - 电压幅度矢量的先前实验演示仅限于1times;3系统^24–26，这不是严格意义上的VMM实现。在这里，我们报告完全模拟的VMM具有足够的精度和高速能效，基于高达128times;64的氧化铪（HfO2）忆阻器横杆³⁶，并通过实验证明了在信号频谱分析，图像压缩和卷积滤波等方面的重要物联网和网络边缘应用价值。

128times;64忆阻器横杆

为了精确调整交叉开关中每个忆阻器的电导，我们将金属氧化物半导体（MOS）晶体管顶部的忆阻器单片集成为每个单元中的接入器件，称为“1T1R”架构。与使用高度非线性忆阻器的无源阵列相比，存储器^14,37–39 或离散选择器设备^40–43 为了减轻潜行路径电流问题，1T1R方案具有较低的封装密度（单元面积的2.5倍）。但是，它允许我们通过晶体管栅极控制独立访问具有线性电流 - 电压（I-V）关系的忆阻器，因此可以精确调谐每个忆阻器的电导。此外，与无源阵列不同，1T1R交叉开关可以使用线性I-V忆阻器实现精确的模拟VMM，从而可以很好地逼近矢量分量和矩阵元素的标量积。晶体管还利用了CMOS平台的成熟度，对于包装密度不是最关键因素的应用具有吸引力。原则上，可以使用在零栅极 - 源极电压下处于“导通”状态的耗尽型晶体管，使得晶体管上的栅极电压仅用于存储器阵列编程，但不用于正常的VMM操作。我们在这个演示中使用了n型增强型晶体管。晶体管的选择及其对泄漏的影响在补充说明1中讨论。通过构建Ta / HfO2/ Pd（参考文献1），在UMass Amherst进行积分。³⁶忆阻器在上面由商业供应商制造的CMOS芯片（更多细节见方法）。数字1b 图1显示了由1T1R阵列组成的集成芯片的一部分，尺寸范围 从4times;4到128times;64。一些单元的详细结构和连接方案如图1所示。1c和补充图1.晶体管的源极线相对于1T1R存储器的源极线设计旋转90°，因此当所有晶体管都打开时，阵列转换成完全连接的忆阻器交叉开关。

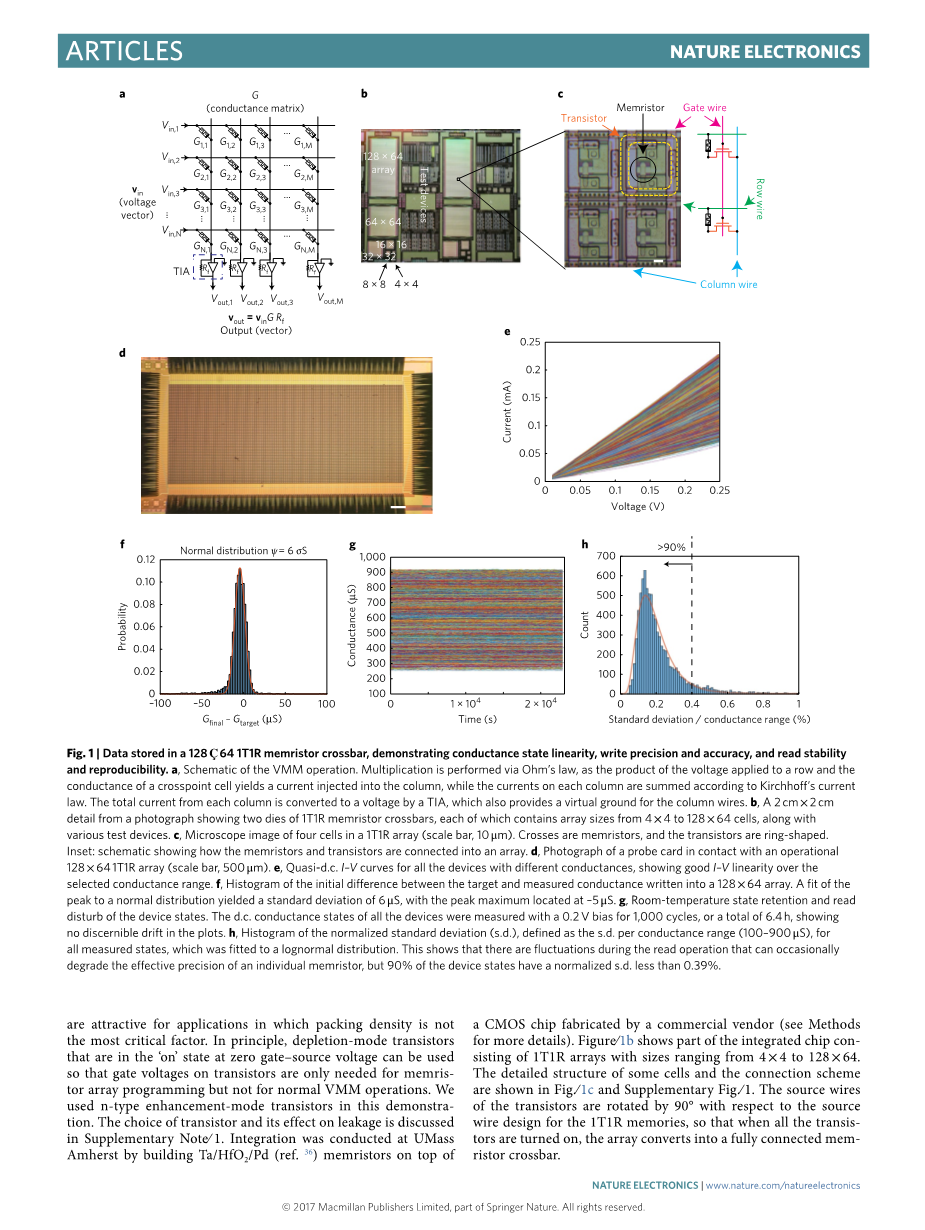
图1 |数据存储在128times;64 1t1R忆阻器交叉开关中，展示了电导状态的线性度，写入精度和准确度，以及读取稳定性和可重复性。a，VMM操作的原理图。乘法通过欧姆定律执行，因为施加到行的电压与交叉点单元的电导的乘积产生注入列的电流，而每列上的电流根据基尔霍夫电流定律求和。每列的总电流通过TIA转换为电压，TIA也为列线提供虚拟接地。b，来自照片的2cmtimes;2cm细节，显示了1T1R忆阻器交叉开关的两个管芯，每个管芯包含4times;4到128times;64个单元的阵列尺寸，以及各种测试装置。c，1T1R阵列中四个细胞的显微镜图像（比例尺，10mu;m）。十字架是忆阻器，晶体管是环形的。插图：显示忆阻器和晶体管如何连接到阵列的示意图。d，与操作128times;641T1R阵列（比

例尺，500mu;m）接触的探针卡的照片。e，所有具有不同电导的器件的准直流I-V曲线，在选定的电导范围内显示出良好的I-V线性度。f，目标和测量电导之间的初始差异的直方图写入128times;64阵列。峰值与正态分布的拟合产生6mu;S的标准偏差，峰值最大值位于-5mu;S。g，设备状态的室温状态保持和读取干扰。所有器件的直流电导状态用0.2V偏压测 量1,000个循环，或总共6.4小时，显示地块没有明显的漂移。h，归一化标准偏差（sd）的直方图，定义为所有测量状态的每电导范围（100-900mu;S）的sd，其符合对数正态分布。这表明在读操作期间存在波动，偶尔会降低单个忆阻器的有效精度，但是90％的器件状态具有小于0.39％的归一化sd。

编程和计算是通过探针卡连接到芯片的定制测试系统实现的（参见方法和补充图2）。数字1d显示一个1T1R方案的阵列大小可以远大于128times;64，但是这个阵列被选择用于演示主要是因为探测器的最大数量 的限制（388，如图所示1d）可用于测试的商用探针卡。以晶体管作为接入设备，我们能够编程几乎所有忆阻器的电导到预定电导范围内的任意值（补充视频1）。我们编写了MATLAB脚本，通过与测试系统通信来控制电阻调整。使用Ta / HfO2/ Pd忆阻器，电池的I-V关系一旦电导大于量子，它就是线性的电导（77.5mu;S）^44,45，如图1e为了传导范围从300到900mu;S，是精确模拟计算的重要特征。典型的电阻切换曲线绘制在补充图3中。在128times;64阵列中的8,192个设备中，编程后只有三个卡在开和15个卡关器件，导致器件响应率达到99.8％。写入误差的直方图，定义为目标电导值与响应忆阻器的测量写入值之间的初始差值，绘制在图4.1f （更多数据，包括来自不同大小的阵列的数据，显示在补充图4中）。当写入容差时，写入误差的峰值符合正态分布，标准偏差sigma;为6mu;S设定为plusmn;10mu;S，并可通过定义a进一步减少MATLAB脚本中的较窄容差和/或使用大量闭环编程迭代，代价是增加编程时间。如果，目前我们打折分布的尾部，它代表少量“粘性”单元格，并将状态之间的间隔定义为a-，我们有在100-900mu;S的电导范围内有效地展示了超过64级电导或6位数字精度，已被证明足以满足机器中的许多任务学习算法^13,15.忆阻器编程操作的精度误差delta;G被认为是写入误差的中值，即-4.7mu;S。为了探索读数的稳定性和可重复性，我们测量了128times;64阵列中具有0.2 V读取脉冲的响应式8,174 装置的电导超过6小时，并且没有看到任何可检测的状态漂移（图2.1g）。单个电池的读取操作存在波动，但这些波动小到足以对多个忆阻器上的列电流测量值产生很小的影响。然而，这些波动是系统最终位精度的良好指标。例如，90％的器件状态在0.39％标准化标准偏差范围内波动（图.1g和补充图5），表示写入精度为128状态或7位，电导范围100-900mu;S。写入误差和读出稳定性与选定的电导范围无关（补充图6和7），证明了利用多级电导的简单性状态。该设备在正常工作温度下保持稳定状态（室温至85°C，补充图8）。稳定的多级电导状态可能是高迁移势垒（测量值1.55 eV）³⁶的结果对于集成在芯片上的Ta / HfO2/ Pd忆 阻器的HfO2 矩阵中形成的富含Ta的电导通道内的Ta阳离子和氧阴离子。

模拟信号处理和图像压缩

我们首先配置数组以实现离散余弦变换（DCT）作为线性变换的典型示例。DCT是一种广泛用于数字的傅立叶相关变换的信号处理和图像/视频压缩和处理^13,46.

在数学上它可以表示为：

其中

其中 （1）

该等式也可以写成矩阵运算：

（2）

其中x是输入信号矢量，M_dct是DCT矩阵，y是输出光谱矢量。

使用交叉开关实现DCT的一个挑战是忆阻器电导值不能为 负，而Mdct 中的一些元素具有负值。为了解决这个问题，这里使用的第一种方法是通过线性变换将矩阵值映射到电导

（3）

其中J是1的矩阵，变换系数由下式确定

（4）

可以从交叉开关的测量输出中恢复DCT

（5）

其中alpha;= v_in/x是与输入电压范围匹配的比例因子，i_out是输出电流的矢量，j是1的矢量。等式的第二项包括对输入电压的所有元素的求和，其可以由软件或硬件进行后处理。

我们采用的第二种方法是使用两个忆阻器（差分对）的电 导差来表示一个矩阵元素。两个相邻行上的输入电压信号具有相同的幅度，但极性相反。差分计算由直流求和执行：

（6）

其中G -G^minus; 是第i行和第j列中的映射矩阵元素，因此可以是负数。差分对还可以通过设置一对设备的电导同时保持另一设备不受影响来缓解卡住或粘滞的设备问题。这种方法为计算提供了一定程度的缺陷容限，但代价是增加了所需的忆阻器单元的数量，从而增加了芯片面积。使用上述第一种方法配置一个64times;64 横杆后，线性变换（方程式（3））将DCT矩阵值映射到忆阻器横杆电导，我们通过绘制实验测量值与每个预期电流的预期电流来定量分析忆阻器DCT的输出精度。编程到交叉开关阵列后的读出电导矩阵如补充图4b所示。原始电流通过简单的缩放在软件中处理（详 见补充说明2和补充图9），可以通过简单的修改设计将其容纳在硬件中，因为原始列电流本身是通过电压输出转换的通过一个TIA。这里报告的DCT的高精度主要是由于高位产生，相对较低的串联电阻（每个块0.35Omega;，每列0.32Omega;）和交叉开关中忆阻器的高I-V线性度从后端过程，如补充表1中所总结的那样。根据我们在补充图中显示的模拟结果，无响应的设备，特别 是那些高电导的设备，对输出精度和功耗有显着的不利

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[609380]，资料为PDF文档或Word文档，PDF文档可免费转换为Word