信道编码及MATLAB仿真实现研究毕业论文
2020-04-01 11:04:17
摘 要
近些年来,通信技术飞速发展,伴随而来的是,信道编码技术在数据存储系统和数字通信系统等领域中得到了日益广泛的应用,同时,现代各种传输方式对于传输可靠性的要求也越来越高,因此信道编码技术在数字传输系统和数字通信等领域的重要性也越发凸显出来。
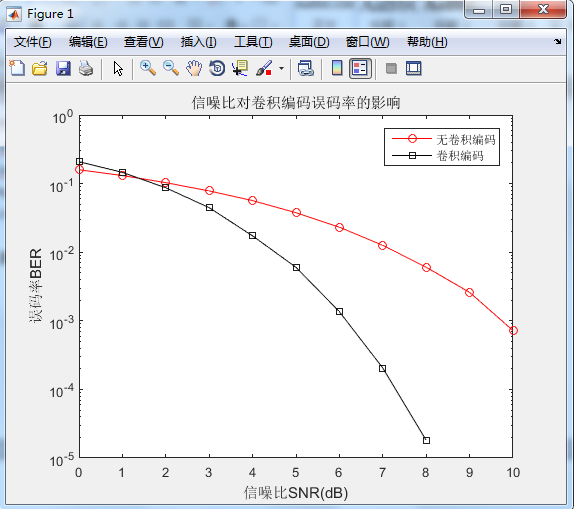
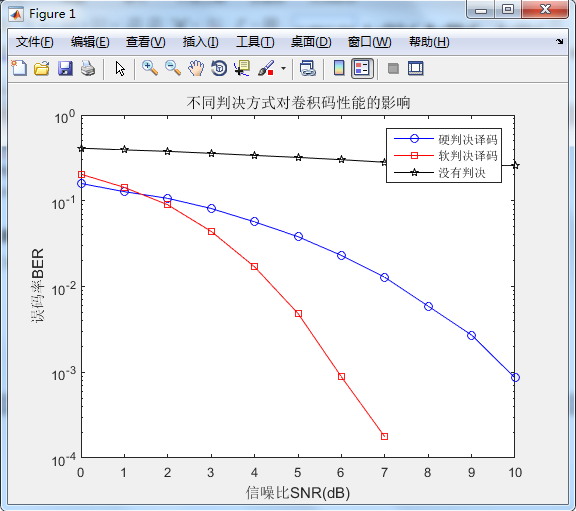
线性分组码和卷积码是信道编码技术的两个重要子类,本次毕业设计就是对线性分组码中的汉明码和卷积码分别进行了编译码的原理分析和模拟仿真实现,仿真平台为Matlab及其提供的Simulink工具包。对于汉明码仿真,我们选取的是(7,4)汉明码,信源输出序列经过汉明码编码之后,分别经过具有不同信噪比的高斯白噪声信道(AWGN)和二进制对称信道(BSC),通过解调和信道编码逆运算之后计算误码率,最后得到并分析汉明码的性能曲线图。对卷积码的仿真,我们则分别利用MATLAB平台和SIMULINK平台来进行,对卷积码分别在高斯白噪声信道和二进制对称信道、分别采用Viterbi软判决和硬判决译码下设置不同的信噪比来观察误码率曲线,分析卷积码的性能。从仿真结果来看,对于汉明码,不管在哪种信道中,随着信道信噪比逐渐提高,信号的误码率会越来越小。对于卷积码,当信道的信噪比比较小时,采用卷积编码的误码率反而高于没有进行卷积编码信号的误码率,而随着信噪比的增大,误码率就有了一个明显的降低,另一方面,卷积码译码采用的判决方式不同,也会对误码率产生影响,一般采用软判决译码误码率要小于硬判决译码,译码效果更好。
关键字:信道编码 MATLAB 误码率 维特比判决
Abstract
In recent years, the rapid development of communication technology has been accompanied by the fact that channel coding technology has been increasingly used in data storage systems and digital communication systems. At the same time, the requirements for transmission reliability of modern transmission methods are also Higher and higher, so the importance of channel coding technology in the field of digital transmission systems and digital communications becomes more prominent.
Linear block codes and convolutional codes are two important subclasses of channel coding technology. This graduation design is the principle analysis and simulation of Hamming codes and convolutional codes in linear block codes, respectively. Simulation platform Simulink Toolkit for Matlab and its. For the Hamming code simulation, we choose the (7,4) Hamming code. After the source output sequence is encoded by the Hamming code, it passes through the Gaussian white noise channel (AWGN) and binary symmetry channel (BSC) with different signal-to-noise ratios. After calculating the bit error rate by performing inverse operations of demodulation and channel coding, the performance curve of the Hamming code is finally obtained and analyzed.For the simulation of the convolutional code, we use the MATLAB platform and the SIMULINK platform to set different SNRs for the convolutional codes on Gaussian white noise channels and binary symmetric channels, respectively using Viterbi soft decision and hard decision decoding. Observe the bit error rate curve and analyze the performance of the convolutional code. From the simulation results, for the Hamming code, no matter what kind of channel, as the signal to noise ratio of the channel increases gradually, the error rate of the signal will become smaller and smaller. For the convolutional code, when the SNR of the channel is relatively small, the error rate of the convolutional coding is higher than that of the convolutionally coded signal, and as the SNR increases, the BER increases. With a significant reduction, on the other hand, the decision method used for convolutional code decoding is different, it will also affect the bit error rate. Generally, soft decision decoding is used to reduce the bit error rate to be less than hard decision decoding. better.
Key words: channel coding MATLAB BER Viterbi decisio
目 录
第1章 绪论 1
1.1 研究的目的及意义 1
1.2 国内外的研究现状 1
1.3 本论文主要研究内容及结构安排 2
第2章 信道编码原理综述 3
2.1 信道编码的概念及任务 3
2.2 常用信道编译码方法 3
2.2.1 分组码 3
2.2.2 卷积码 3
2.2.3 循环冗余码 4
2.3 信道分类 4
2.3.1 二进制对称信道(BSC) 4
2.3.2 二进制删除信道(BEC) 5
2.3.3 高斯白噪声信道(AWGN) 5
2.4 本章小结 6
第3章 线性分组码分析及仿真实现 7
3.1 线性分组码基本理论 7
3.1.1 线性分组码的定义 7
3.1.2 生成矩阵和校验矩阵 7
3.2 线性分组码编码方法 8
3.3 线性分组码译码方法 8
3.4 汉明码及MATLAB仿真 9
3.4.1 汉明码定义 9
3.4.2 汉明码对高斯白噪声信道的仿真 9
3.4.3 汉明码对二进制对称信道的仿真 11
3.5 本章小结 13
第4章 卷积码分析及仿真实现 14
4.1 卷积码基本理论 14
4.1.1 卷积码的基本概念 14
4.1.2 卷积码编码原理 15
4.1.3 卷积码译码原理 15
4.2 卷积码matlab仿真 15
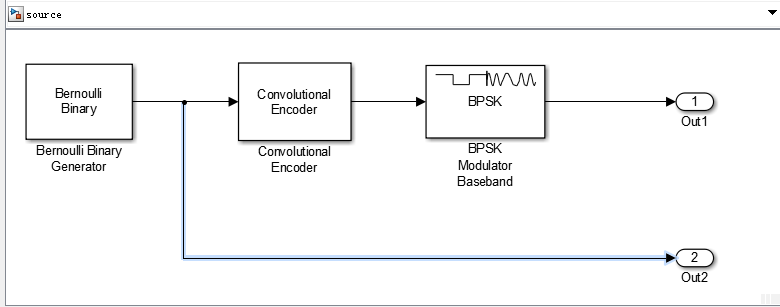
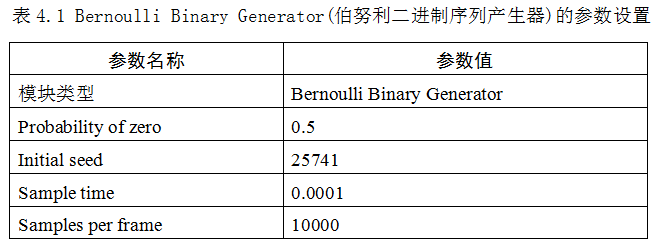
4.2.1 卷积码编码及matlab仿真 15
4.2.2 卷积码译码及matlab仿真 16
4.3 卷积码simulink仿真 17
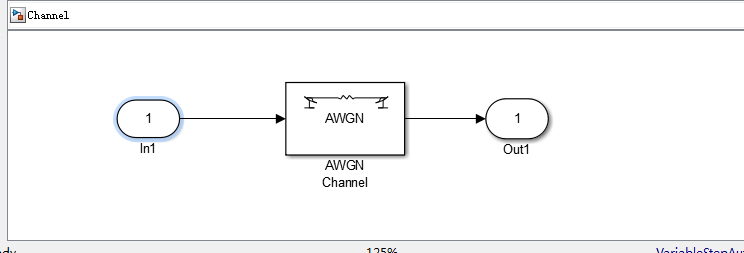
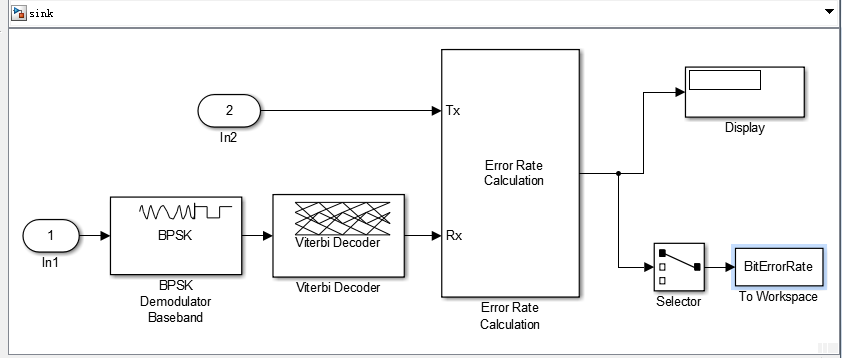
4.3.1 卷积码译码器对高斯白噪声信道 17
4.3.2 卷积编码器在二进制对称信道(BSC)中的性能 24
4.3.3 卷积码译码器对二进制对称信道和高斯白噪声信道仿真比较 27
4.4 本章小结 28
第5章 总结与展望 29
5.1 总结 29
5.2 展望 29
参考文献 30
致谢 31
第1章 绪论
1.1 研究的目的及意义
我们评价一个信息传输系统的好坏,要看信息输入这个系统后,是否能在输出端没有错误的恢复出来。我们希望信息在信道中传输时能够速度快,质量好,数量多,频带省,另一方面,客观规律又是客观存在,违背不了的。第一,考虑信息传输速度,它注定是一个有限值,总是会小于这个信道的信道容量,第二,信号在信道里传输,一定会受到来自信道的各方面的影响,不可避免的会发生传输错误,我们能做的也只是利用信道编码技术,增加一定的冗余度来让信号在信道中更可靠的传输。
信道的信息率R作为度量信息传输速度的参数,它的最大值就是信道容量C。而我们通常利用平均差错率Pe来衡量一个信息传输系统的可靠性,即平均差错率Pe越小,传输系统越可靠。通常我们可以先对待传输的信息进行信道编码,以此减小平均差错率。根据香农的有噪信道编码定理,平均差错率有可能在某种恰当的信道编码和译码下趋近于零。
现如今,通信技术的发展突飞猛进,随之而来的是信道编码技术在各种的通信系统中得到了广泛的应用。用户日益对通信质量提出了越来越高的要求,使得我们的信道编码技术显示出了越来越大的重要性。
1.2 国内外的研究现状
现代信息和编码理论的创始人香农(C.E.Shannon),在1948年提出了有噪信道编码定理即香农第二编码定理,定理启发了我们如何进行可靠的信息传输,并给出了信道容量C的概念,这为后来的信道编码理论的发展奠定了基础。
在数字通信系统中,信道码无处不在:在信道条件较好的有线通信系统(包括光纤通信系统)中主要使用简单的线性分组码:其子类BCH码广泛的应用于移动通信系统中;在卫星通信领域,RS码和卷积码及其级联码,已经成为最为广泛用到的信道编码。近年来,Turbo码、Turbo乘积码(TPC)和LDPC码在卫星和深空通信、第三代移动通信、数字视频广播(DVB-S)等领域都得到了一定的应用[1]。
1.3 本论文主要研究内容及结构安排
根据有噪信道编码定理,平均差错率有可能在某种恰当的信道编码和译码下趋近于零。然而,香农并没有给出具体的可行的方法,因此,我们需要针对具有不同干扰特性的各种信道选择采用编码效率高、抗干扰性能好的信道编码,使待传送的信息率R小于信道容量C的条件下,尽可能地降低平均差错率Pe,提高信息传输的可靠性。找到与给定的信道模型形成最佳匹配的信道编码,就是这次研究的基本内容和目标。
本次论文一共有5个章节,下面为论文的结构安排:
第1章,绪论,介绍信道编码的研究目的及意义以及现如今国内外的研究现状。
第2章,信道编码原理综述,介绍有关信道编码的基本原理以及一些常用的信道模型。
第3章,线性分组码分析及仿真实现,深入介绍线性分组码的理论及编译码方法,并在MATLAB平台仿真实现。
第4章,卷积码分析及仿真实现,深入介绍卷积码的基本理论,分别在MATLAB平台和Simulink平台进行卷积码的仿真实现。
第5章,总结与展望,这一章总结了本次的毕业设计,得出研究结论,同时对信道编码技术提出展望。
第2章 信道编码原理综述
2.1 信道编码的概念及任务
信道编码作为一种控制信号传输错误的方法,在现代通信领域中得到广泛的应用。信道编码过程,简单的说就是发送信息的一方将,以某种方式计算信息序列得到的相应的检错码或纠错编码,附加到信息序列之后,并在被载波调制后送到信道进行传输。接收端解调接收信号,得到二进制序列,它包含了原始的信息序列和检错或纠错编码。对这个序列进行信道编码的逆过程后,就获取了我们需要的信息序列,也获取了是否有着传输错误的信息。若某个信道编码只能够检错,它可以让发送端重传信息,以此纠正发生的错误;若某个信道编码除了检错之外还有纠错功能,并且误码个数在信道编码纠错能力范围之内,它就有概率纠正发生的传输错误。
已调信号在信道中传输,不可避免的会受到来自于信道的,各种方面的影响。所以,我们可以利用信道编码技术,来纠正这些由于在信道中传输而发生的错误,减少信道的影响,减小误码率。信道编码技术的原理,就是增加某些的冗余度到信号中,加入的冗余度在接收时用来检查并纠正信号在信道中通过时可能会产生的错误。
2.2 常用信道编译码方法
通常把常用的信道编译码方法分为三种类型,即卷积码、分组码和循环冗余码(严格地说,循环冗余码属于信源编码,把它放在本章里是为了论述的方便)。
2.2.1 分组码
分组码也是一种利用一定的冗余度来完成对信号的纠检错功能的编码方法,通常它让输入序列变的更长输出。分组码的基本思想是对信息序列分段编码。
BCH码的名称来源于其3个发明人的名字,是一种可以纠正很多个随机错误的循环码,是分组码的一种重要的子类。RS码是由Reed和Slolmon提出来的,一种多进制的BCH码,它有非常强大的检错纠错能力,可以纠正突发的错误是它的突出特点。
2.2.2 卷积码
卷积码是另外一种常用信道纠错码。我们知道,卷积码与分组码的最大区别是,编码过程中的输出码字不仅和这个组的输入信息有关,而且与前面几个组的输入也有关系。另外,各个码组之间还有着关联关系,即本组的输入信息会对其后的几个码组的输出产生影响。
约束长度、生成多项式、反馈多项式共同构成了卷积码的多项式表示。除此之外,也可以利用trellis图来表示卷积编码。
卷积编码可以分成基本卷积码和收缩卷积码两类。基本卷积码的纠错能力很强,但是编码效率比较低,仅为二分之一。若要使编码效率更高,此时另一种卷积码—收缩卷积码可以派上用场。它的编码效率可以达到二分之一、三分之二、四分之三、六分之五甚至八分之七,但收缩卷积码的纠错能力相应减弱。
2.2.3 循环冗余码
循环冗余码也是经常用到的一种检错编码。但是它没有纠错功能,这一点和分组码是不同的。信道发生的传输错误一旦被接收信号的一端检测到,它会令发送方再将这个信息序列发送一遍,而不是去纠正错误。
2.3 信道分类
顾名思义,对于一个信道来说,它的功能就是传输信号。通常我们把由有线或者无线电线路提供的信号通道称为信道。
从不同意义上来划分,有广义信道和狭义信道之分,对于广义信道来说,也有编码信道和调制信道之分。
下面介绍一些经常会用于通信系统仿真中的信道模型,并对MATLAB提供的相关函数进行一些解释和说明。
2.3.1 二进制对称信道(BSC)
二进制对称信道是一类很简单的信道,它的输入是离散信号,输出也是离散信号。发送“0”,而收到的符号被判决成“1”的概率是p,正确判决的概率是1-p,发送数据为“1”时也是一样,因此我们称信道为对称信道。其模型如图2.1所示。
1-p
0
0
1
1
1-p
p
p
图2.1
事实上,二进制对称信道是将输入比特按照概率p翻转,所以能够比较好的应用于测试硬判决译码的纠错性能[1]。
在MATLAB语言中,二进制对称信道的仿真函数是bsc,其语法结构为:
ndata=bsc(data,p)
ndata=bsc(data,p,state)
[ndata,err]=bsc(...)
其中输入参数data为二进制输入信号,输入参数p为二元对称信道的错误概率。第二种语法结构中包含输入参数state,用于将均匀随机数发生器的状态复位到state表示的整数。
2.3.2 二进制删除信道(BEC)
另一种信道二进制删除信道(BEC)的转移概率如图2.2所示。当发送端发送“1”或“0”时,接收方正确接收的概率为1-a,而有a的概率发送的消息被删除。
图2.2
e
1-a
a
a
0
1
0
1
1-a
2.3.3 高斯白噪声信道(AWGN)
信号在信道中传输,就一定会受到各种各样的影响,我们把信号受到的这些影响称为“噪声”。其中最简单和常见的一类噪声就是加性高斯白噪声,它的方差为噪声功率的大小,均值为0。
高斯白噪声信道即加入高斯白噪声到信号上,一般我们用信道信噪比SNR来表示添加的高斯白噪声的程度和幅度,通常我们规定信号功率和噪声功率的比值(dB)为信噪比。
在MATLAB语言中,用函数awgn来进行高斯白噪声信道仿真,其用法有
b=awgn(a,snr)
b=awgn(a,snr,sigpower)
函数表示在输入a中加入高斯白噪声,有噪信号b从高斯白噪声信道另一端输出。snr以dB的形式来指定每个采样的信噪比。
2.4 本章小结
这一章比较详细的阐述了信道编码的相关原理,介绍了卷积码、分组码、循环冗余码这些常用信道编译码方法,还介绍了二进制对称信道、高斯白噪声信道等常用到的信道模型。
第3章 线性分组码分析及仿真实现
3.1 线性分组码基本理论
通常用于前向纠错的分组码,一般表示为(n,k)的形式,是一组长度一定的码组。分组码把k个信息位长度编成n位长度,我们将加到k个信息位之后的n-k位信息称为监督位,以完成检错和纠错的功能。若监督码元和信息码元为线性关系,我们就称这种分组码为线性分组码,此时可以用矩阵变换来表示编码过程。
我们可以注意到,分组码码字的生成和前后的数据没有关系,而仅仅和当前的输入数据有关。相应的,码字的生成和前后数据相关的编码称为卷积码。
3.1.1 线性分组码的定义
分组码对信息序列进行分段编码。如果对包含k个码元的信息组M
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: