基于LMS算法的自适应滤波器研究与实现毕业论文
2020-02-17 23:13:20
摘 要
自适应信号处理是统计信号处理的重要分支,在很多方面都有所应用,例如通信,控制,声纳,地震和生物医学等方面。因此,自适应滤波器也在这些领域有很重要的应用。对自适应滤波器的研究正变得越来越活跃。它在未知统计环境或非平稳环境下处理各种信号有着非常优越的性能,远超常规方法设计的固定滤波器。自适应滤波器有很强的自学习能力,并且其算法较为容易实现,这让它在检测增强噪化信号,它可以抵消噪声干扰,在通信系统的自适应均衡和未知系统的识别中具有广泛的应用[1]。
自适应滤波器是一种自行设计的滤波器,它利用递归算法来执行操作。这赋予了滤波器在不能完整获取信号特征知识的情况下却能完成滤波运算的能力。这种算法需要从一些初始设定的条件集出发,得到一个递归的初始值,也就是自适应滤波器的初始参数值。自适应滤波器的参数将从一个自适应循环更新到下一个。研究自适应滤波器可以去除输入信号中的噪声信号,可以识别未知动态系统的系统,并可用于预测未知信号。
本文首先介绍了自适应滤波器的理论基础,主要从自适应滤波理论的讨论和自适应滤波器的结构分析以及所选滤波器的结构分析入手。然后,介绍了两种自适应滤波算法,主要是LMS算法的推导。最后,使用Matlab分别模拟两种算法,主要是LMS算法,首先用不同的信噪比信号测试LMS自适应滤波器。然后分析影响其滤波和自适应性能的因素,并与RLS算法设计的滤波器进行比较和分析。分析各自的优越性和局限性。实验表明:LMS自适应滤波器的收敛速度与步长因子有关,其滤波性能与滤波器的阶数有很大关系。RLS的收敛速度非常快,但它需要大量的计算,而RLS的过滤效果可能与其遗忘因子有关。总的来说,在不同情况下,两种算法有各自的优越性,当要求收敛速度较快时,用RLS算法更好,例如在信号增强器中;而如果需要其设计简单或是较好的鲁棒性则采用LMS更好例如在自回归预测器中。
关键词:自适应滤波器; LMS算法; RLS算法
Abstract
Adaptive signal processing is an important branch of statistical signal processing, which is used in a wide range of applications, such as communications, control, sonar, seismic and biomedical applications. Therefore, adaptive filters also have important applications in these fields. Research on adaptive filters is becoming more and more active. It has excellent performance in dealing with various signals in unknown statistical environment or non-stationary environment, far exceeding the fixed filter designed by conventional methods. The adaptive filter has strong self-learning ability and its algorithm is easy to implement, which makes it widely used in detecting enhanced noise signal, canceling noise interference, adaptive equalization of communication systems and identification of unknown systems.
An adaptive filter is a self-designed filter that uses recursive algorithms to perform operations. This gives the filter the ability to complete the filtering operation when it can not acquire the signal feature knowledge completely. This algorithm needs to start from some initial set of conditions and get a recursive initial value, that is, the initial parameter value of the adaptive filter. The parameters of the adaptive filter will be updated from one adaptive loop to the next. The study of adaptive filter can remove the noise signal in the input signal, identify the system of unknown dynamic system, and can be used to predict the unknown signal.
Firstly, this paper introduces the theoretical basis of adaptive filter, starting with the discussion of adaptive filter theory, the structure analysis of adaptive filter and the structure analysis of the selected filter. Then, two kinds of adaptive filtering algorithms are introduced, mainly the derivation of LMS algorithm. Finally, two algorithms are simulated by using matlab, mainly LMS algorithm. First, LMS adaptive filter is tested with different signal-to-noise ratio signals. Then, the factors affecting its filtering and adaptive performance are analyzed and compared with the filters designed by RLS algorithm. Analysis of their advantages and limitations. Experiments show that the convergence speed of LMS adaptive filter is related to the step factor, and its filtering performance is closely related to the order of the filter. The convergence rate of RLS is very fast, but it needs a lot of calculation, and the filtering effect of RLS may be related to its forgetting factor. Generally speaking, the two algorithms have their own advantages in different situations. When the convergence speed is required to be faster, RLS algorithm is better, such as in signal intensifier, while LMS is better in autoregressive predictor if its design is simple or its robustness is better.
Keywords adaptive filter; LMS algorithm; RLS algorithm
目 录
第1章 绪论 1
1.1 课题研究的背景与意义 1
1.2 国内外的研究现状分析 1
1.3 研究的基本内容及论文的结构安排 2
第2章 自适应滤波器理论基础 3
2.1 自适应滤波器工作原理 3
2.2 自适应滤波器结构 3
2.3本章小结 4
第3章 自适应滤波算法 5
3.1 最速下降算法 5
3.2 LMS算法 6
3.3 RLS算法简介 7
3.4 本章小结 8
第4章基于Matlab的自适应滤波器仿真 9
4.1 整体仿真设计 9
4.2 LMS算法设计 10
4.2.1 LMS算法设计思路 10
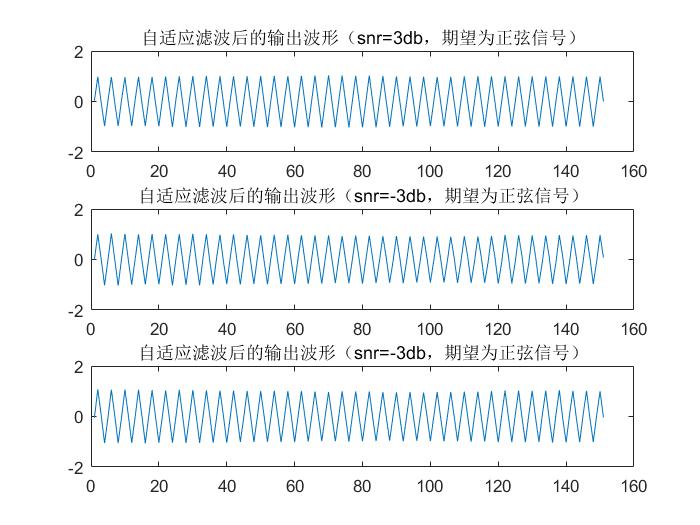
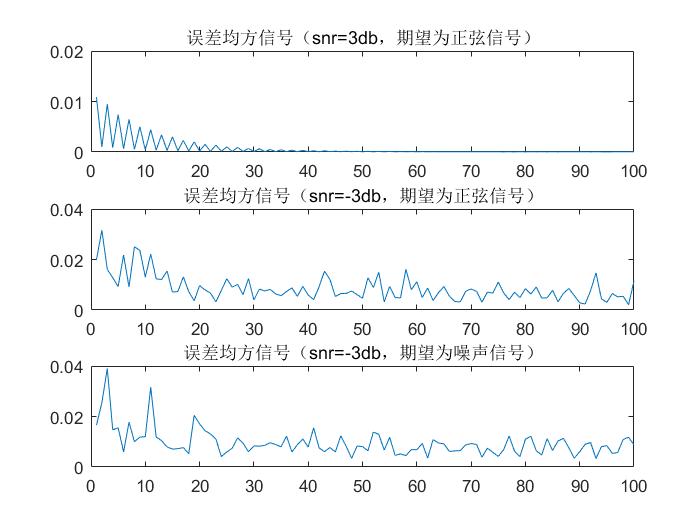
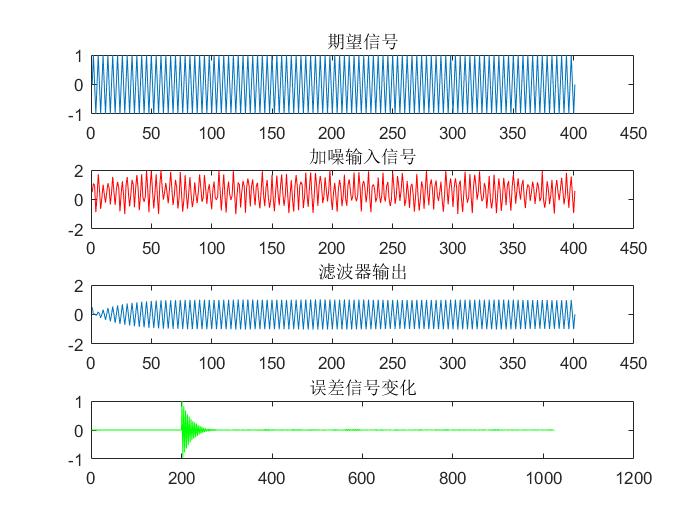
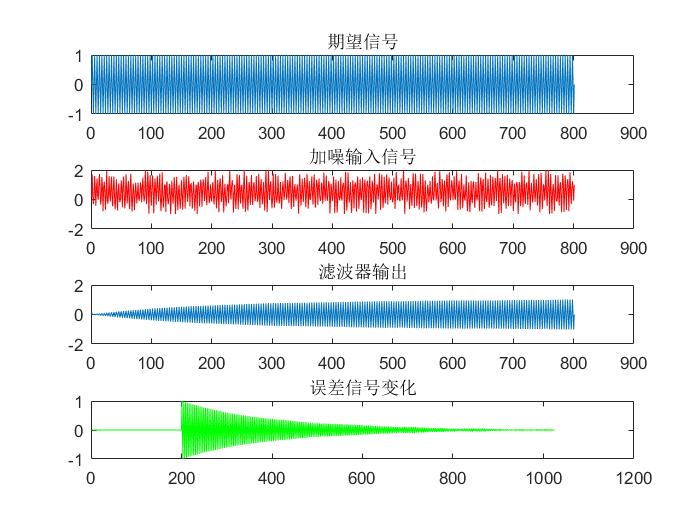
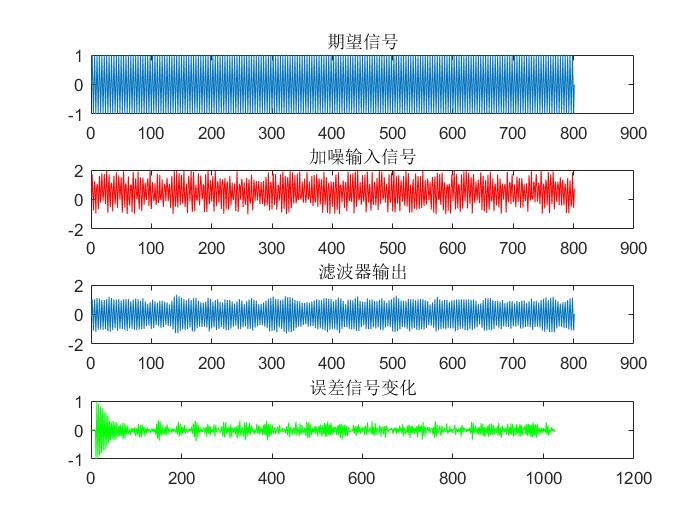
4.2.2 LMS算法仿真结果图 11
4.2.3 步长因子u对LMS自适应滤波器的影响 12
4.2.4 滤波器阶数对LMS自适应滤波器的影响 15
4.3 LMS算法与RLS算法对比仿真 17
4.3.1 RLS算法设计 17
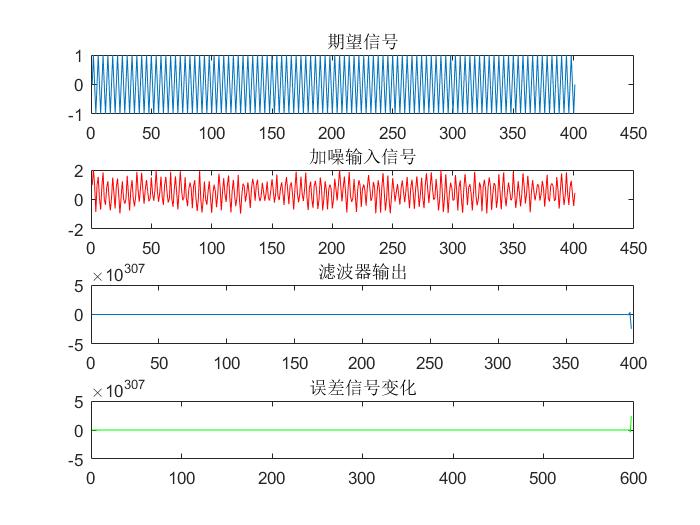
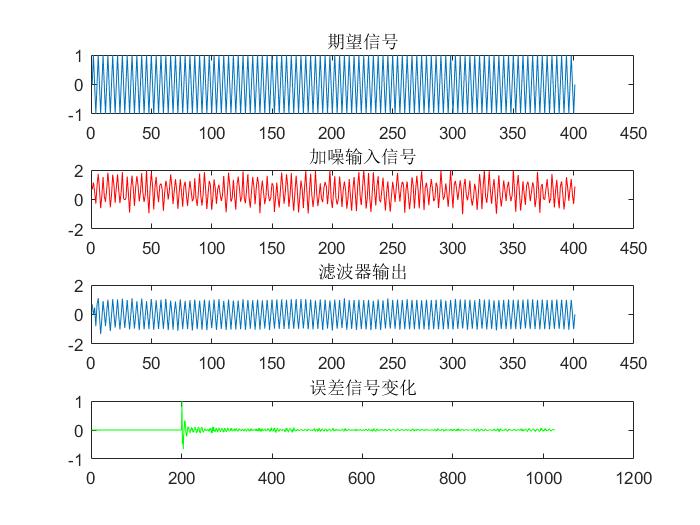
4.3.2 LMS算法与RLS算法仿真对比 18
4.4本章小结 21
第5章 总结与展望 22
5.1总结 22
5.2展望 22
参考文献 23
致 谢 24
附录A 25
第1章 绪论
1.1 课题研究的背景与意义
滤波器通常用于从接近指定质量的感兴趣的噪声信号中提取信息,并且是滤除噪声和干扰的手段。传统的滤波器设计需要知道正在处理的数据的统计方面的先验知识,例如维纳滤波器,只有当输入数据的统计特性与滤波器滤波特性兼容时,该滤波器才能最优,我们可以采用“估计”与“插入”来解决这种困难。首先,估计相关信号的统计参数,将结果插入非递归公式来计算滤波器参数。但在实时运算中,要设计这样的系统比较困难,并且需要价格高昂的硬件。如果采用可以消除这种限制的系统,则该系统意味着滤波器是自行适应的,即,自适应滤波器依赖于递归算法来实现改变滤波器的参数操作。这使得可以在没有相关信号的完整统计特性的情况下执行滤波操作。
自适应滤波器通常分为线性和非线性,在很多资料中已经研究过多种递归算法,而其中线性滤波器有两种主要的推导方法。一种是最小二乘法,基于该方法获得递归最小二乘(RLS)算法。一种是随机梯度下降法,基于该方法获得最小均方(LMS)算法。还有基于两种算法的改进算法如:归一化(NLMS)算法,平方根自适应滤波器(QRD-RLS),算法变步长(SVSLMS)算法等[2]。最小均方误差(LMS)算法的核心思想是以最小均方误差为标准,从而最小化输出信号和期望信号之间的均方误差。最小均方误差(LMS)算法因其算法简易,运算量小,稳定性强,容易实现而被广泛使用[3]。但其缺点是收敛速度慢且数学上研究困难。这些算法特点不一,在不同的场合有不同运用。
1.2 国内外的研究现状分析
1942年,Wiener以最小均方误差为准则研究了加性噪声中信号的最优滤波问题。 使用Wiener.Holf方程给出了连续信号情形的最优解。
在20世纪60年代早期,卡尔曼突破并发展了经典滤波理论,并提出了一种时域状态空间方法。他还提出了一组易于在计算机上实现的递归滤波算法,并将其应用于非平稳过程[6]。
最早的自适应滤波算法是最小的LMS算法。它成为一种简单有效的横向滤波算法。实际上,LMS算法是随机梯度算法,其在误差信号的梯度方向上相对于抽头权重的平方迭代地调整每个抽头权重。1994年,Sayed和Kailath建立了卡尔曼滤波器和RLS算法之间的对应关系,使人们对RLS算法有了更深入的了解,通过将卡尔曼滤波器应用于自适应滤波已经实现了许多结果[4]。
目前,现代信号处理理论的发展也极大的促进了自适应滤波技术的发展。 特别是小波技术和人工智能理论的发展促进并加速了自适应滤波技术的进步。
自适应滤波器目前在算法方面已经研究的比较成熟,主要还是在硬件方面进行改进,目前主要有两大类,基于 DSP通用数字信号处理器的实现方法及 FPGA可编程门阵列的实现方法。
LMS算法由于其运算简单且性能有效,使得其硬件设计更简单而获得了大量实际应用。尽管RLS算法具有更快的收敛速度,但其运算复杂度很大,使得其硬件实现更加困难。
因此,本文主要研究基于LMS的自适应滤波器。
1.3 研究的基本内容及论文的结构安排
本文主要采用LMS算法研究自适应滤波器的原理和应用,设计了一种FIR结构的自适应滤波器来对含噪信号模拟仿真。 通过对比滤波后的输出信号和原始信号的波形差异,衡量自适应滤波器对噪声的滤除能力及分析影响滤波效果和收敛速度的因素,并与使用 RLS算法的自适应滤波器进行比较。
该研究的关键问题是FIR结构的自适应滤波原理和结构分析以及LMS算法的研究和理解。因此,我从以下几个方面入手。
(1)学习FIR结构的滤波原理,学习LMS算法的原理和推导。
(2) 在对以上内容进行充分学习后,开始进行简单的蒙特卡偌仿真,先设计出能够进行自适应滤波的MATLAB程序。
(3) 根据要求对程序添加功能完成对研究内容的分析。
本文结构如下:
第一章:首先,阐明了自适应滤波器的背景和研究意义。
第二章:阐述了自适应滤波器的基本理论,介绍了自适应滤波器的工作原理和其结构形式。注重于对自适应滤波器中最常用的FIR横向滤波器结构的研究。
第三章:基于前一章,描述了两种自适应滤波算法,即最小均值(LMS)算法和递归最小二乘(RLS)算法。 详细推导了LMS算法,并简要介绍了RLS滤波器的推导过程及工作原理。
第四章:基于以上两种算法,即LMS算法和RLS算法的自适应滤波器,进行了MATLAB仿真实验,对其性能与影响其性能的参数进行了研究,分析了每种参数对自适应滤波器产生的影响。并且 LMS算法和 RLS算法各有优缺点,它们各有自己适用的范围。
第2章 自适应滤波器理论基础
2.1 自适应滤波器工作原理
自适应滤波器是一种滤波器,这种滤波器可以根据输入信号的变化使用自适应滤波算法调整滤波器参数或改变滤波器结构。通常,自适应滤波器不改变结构只改变滤波器的某些参数。一般而言,我们所说的自适应,就是滤波器可以通过输入信号的统计特性来自发的调整滤波器的某些参数[8],从而满足某种最优准则。
自适应滤波器可以分为两部分自适应算法及可调参数得数字滤波器具体如图所示:
e(n)
参数可调的数字滤波器
自适应算法
x(n)
∑
-
d(n)
y(n)
图2.1自适应滤波器的结构图
在图中,x(k)输入信号通过可调参数的数字滤波器输出,以产生输出信号 y( k),并且将期望信号 d( k)与输出信号 y( k)相减,得到误差信号 e( k)。e(k)和x(k)利用自适应算法调整滤波器的权重参数,从而最小化误差信号e(k)。重复上述过程,滤波器在工作中不断了解从而估计出输入信号和噪声的统计规律,并在此基础上自发地调整滤波器参数,达到最优滤波效果[5]。输入信号的统计规律发一旦产生改变,数字滤波器就会自动追踪输入信号的变化情况,从而调整滤波器的权重参数,实现滤波效果,完成自适应过程。
2.2 自适应滤波器结构
线性滤波器算法主要有两个过程: (1)滤波过程,用来对所输入数据产生输出响应;(2)自适应过程,用来提供一种用于滤波过程的可调参数随输入数据自适应变化的控制算法[6]。 两个过程相互影响,相互制约。
线性滤波器的冲激响应决定其记忆能力由此可以分为有限记忆和无限记忆滤波器[7]。无限记忆滤波器一般都是无限冲激响应滤波器。一般由于无限冲激响应(IIR)滤波器存在稳定性问题,所以通常不使用此种滤波器。
在有限存储器滤波器中,存在三种类型的滤波器结构,即抽头延迟线滤波器(FIR横向滤波器),晶格滤波器和脉冲阵列,本文主要使用更常用的FIR横向滤波器。
其由如图所示的三个基本单元构成:(1)单位延迟单元,(2)乘法器,(3)加法器。滤波器延迟单元的数量确定脉冲响应的持续时间,其通常被称为滤波器阶数[8]。延迟单元用单位延迟算子来表示。乘法器用于乘以滤波器系数和连接到它们的抽头输入,加法器对乘法器的输出求和,以获得总滤波器输出。对于图中滤波器输出为
(2.1)
FIR滤波器结构如图所示:
…
…
…
输入u(n)
u(n-M)
u(n-1)
u(n-2)
输出y(n)
图2.2 FIR横向滤波器的结构图
2.3本章小结
本章介绍了自适应滤波的基本理论,并介绍了自适应滤波器的一般结构,主要包括两个方面:滤波结构和自适应算法。在滤波结构上,经典自适应滤波器选择横向滤波器进行滤波。主要介绍了水平自适应滤波结构,它是经典滤波器使用最常用的滤波器结构。
第3章 自适应滤波算法
3.1 最速下降算法
对于维纳滤波器,如果使用Wyna-Hoff方程的形式计算滤波器的参数,则当统计变化时,需要大量的相关矩阵的逆。如果有一种算法可以随时间跟踪信号统计量,那么只要它是平滑的,你就不必每次都解决Wiener-Hoff方程。给定任意抽头权重向量,其解决方案将随着自适应循环数量的增加而改善。
最速下降算法提供了一种解决方案,其解决方案可以收敛到Wiener解决方案,并且不需要输入向量相关矩阵的逆。
一个代价函数,是某个未知向量w的连续可微函数,我们要找一个最优解,使他满足
(3.1)
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: